基于自适应反演滑模控制的上田振子系统混沌控制

梁小文，赵小山，武凯莉

（天津职业技术师范大学理学院，天津300222）

基于自适应反演滑模控制的上田振子系统混沌控制

梁小文，赵小山，武凯莉

（天津职业技术师范大学理学院，天津300222）

针对不确定混沌系统的控制问题，提出一种自适应反演滑模控制的方法。分析了上田振子系统模型的混沌动力学行为，采用自适应反演滑模控制器对此混沌系统进行控制。自适应控制方法可以实现对系统不确定性上界的估计，从而增强控制系统的鲁棒性和自适应性。仿真结果验证了此方法的有效性。

混沌系统；反演滑模控制；自适应律；鲁棒性

混沌是指确定性动力系统的长期行为对系统初始状态异常敏感，却又不发散，而且无法精确重复的现象，它是非线性系统普遍具有的一种复杂动力学行为，被认为是20世纪最重要的科学发现之一。由于混沌的长时间不可预见性和内在的随机性，混沌输出常常不符合人们的要求，因而抑制混沌成为控制混沌的一个重要任务［1-2］。在混沌控制的研究中，人们先后提出了诸多混沌控制的方法，如自适应控制法［3］、脉冲控制法、延迟控制法、滑模变结构控制法［4-6］、模糊控制法和神经网络控制法等。近年来，混沌的控制和应用研究已经在物理学、力学、信息、化学、电子、计算机、通讯与信息加密等工程技术领域取得了可喜的成果，展现出广阔的发展前景。反演控制设计方法是在非线性控制领域中提出的一种新方法。其基本思想是将复杂的非线性系统分解成不超过系统阶数的子系统，引入虚拟控制作为中间变量，为每个子系统确定李雅普诺夫函数，并设计虚拟控制变量，一直“后退”到整个系统，直到完成整个控制律的设计。反演法在处理系统不确定性，尤其是非匹配不确定性方面具有很大优势。反演设计法通常需要假定非线性系统中的未知参数具有线性参数化的形式，并且系统中的非线性函数必须精确已知，这在实际中很难得到满足。为解决这一问题，必须将反演法与其他控制方法相结合［7-10］。本文以上田振子系统为模型，通过对其非线性动力学行为的分析，运用数值仿真验证了混沌的特性，并用自适应反演滑模方法控制了该系统的混沌，将其控制到目标轨道。

1　上田振子系统的动力学分析

1.1上田振子混沌系统的模型及其混沌吸引子考虑如下形式的上田振子系统：

式中：m、c和k均为系统的参数；F0和ω分别为外加周期激励信号的振幅和频率。取：m=1、k=1、ω=1、c=1、F0=1，取系统初值（0，0.01）。运用Matlab软件计算系统的Lyapunov指数，得λ1=0.098、λ2=-0.148，其中有一个正的Lyapunov指数，说明系统在该组参数下进入了混沌状态。

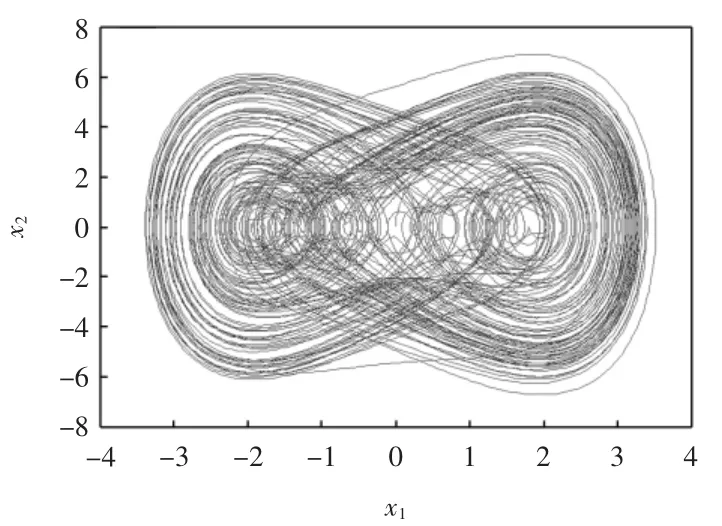
图1　系统吸引子图

由图1可以看出，系统的吸引子有具很强的吸引性及复杂的折叠和拉伸轨线，这种具有复杂结构的吸引子被称为奇怪吸引子，而具有奇怪吸引子的运动就是混沌的。

1.2庞加莱截面图

在相空间中，可以适当选取一个截面，这个截面可以是平面也可以是曲面。根据运动系统的相空间连续轨迹与庞加莱截面的截点情况，判断该系统有无混沌运动，这样的截面称为庞加莱截面。当庞加莱截面上有且只有一个不动点或少数离散点时，运动是周期的；当庞加莱截面上是一封闭曲线时，运动是准周期的；当庞加莱截面上是一些成片的具有分形结构的密集点时，运动便是混沌。系统在上述参数和初值下的庞加莱截面如图2所示。由图2可以看出，截面上所呈现的是一些成片的具有分形结构的密集点。因此，此系统的运动是混沌的。

图2　系统庞加莱截面图

1.3Lyapunov指数图

Lyapunov指数是指在相空间中，初始条件不同的2条相邻的轨迹随时间按指数收敛或发散的比率。混沌系统中，初始条件的微小变化将使轨迹最终变得截然不同。系统要产生混沌必须具有正的Lyapunov指数。系统在上述参数和初值下t→∞时的Lyapunov指数曲线如图3所示。

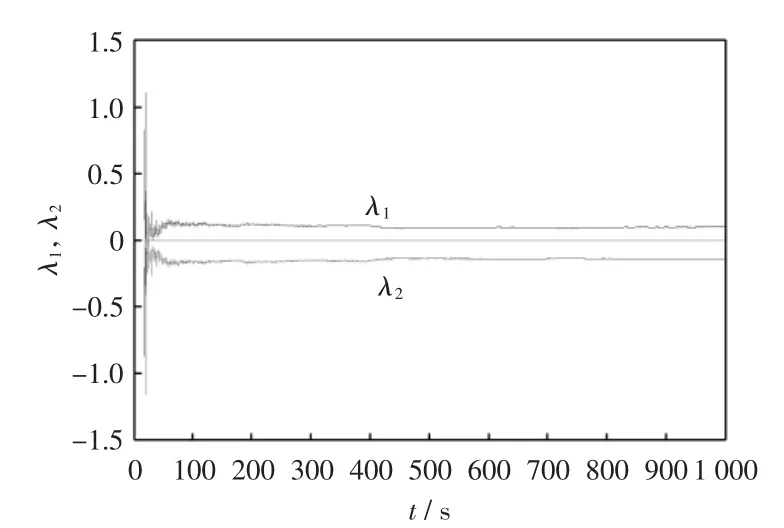
图3　系统李雅普诺夫指数图

根据Matlab仿真结果得出，随着时间的推移，系统的2个李雅普诺夫指数最终都趋于一固定常数。这2个常数分别为λ1=0.098和λ2=-0.148，其中λ1= 0.098为正，则系统产生混沌。

2　上田振子混沌系统反演滑模控制器设计

2.1系统描述

被控系统为：

式中：d（t）为外加干扰；ΔA、ΔB、ΔC和ΔD均为系统参数不确定部分。

将式（2）写为：

式中：F为总不确定性，其表达式为：

在实际情况下，通常存在未知的不确定因素和外在干扰因素，总不确定性F的上界很难确定。在这种情况下就可以尝试运用自适应的控制方法对F进行估计［5-7］。

2.2自适应反演滑模控制器的设计

假设位置指令为xd，控制器设计步骤如下。

（1）跟踪误差为z1=x1-xd，则

定义Lyapunov函数

式中：c1＞0；z2为虚拟控制项。则

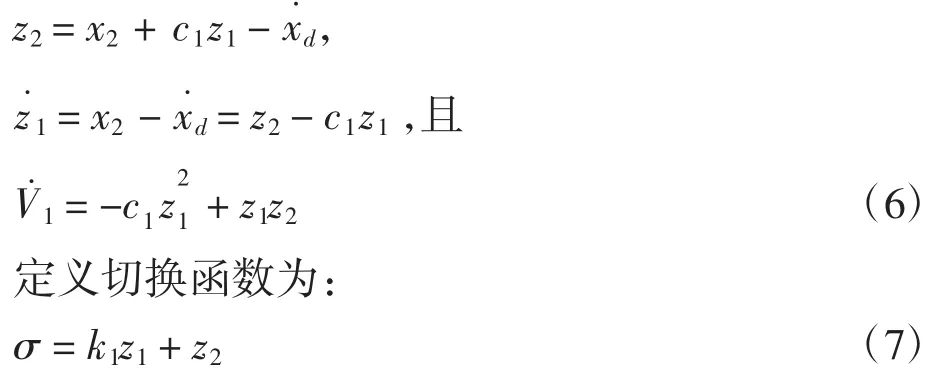
式中：k1＞0。

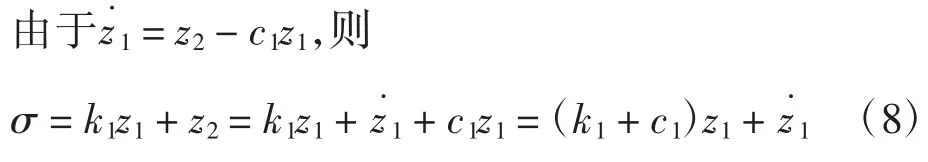
由于k1+c1＞0，如果σ=0、z1=0、z2=0，则。为此，需要进行下一步设计。

（2）定义Lyapunov函数

则

（3）假设参数不确定的部分和外在的干扰部分变化是缓慢的，取。

定义Lyapunov函数

设计自适应控制器为：

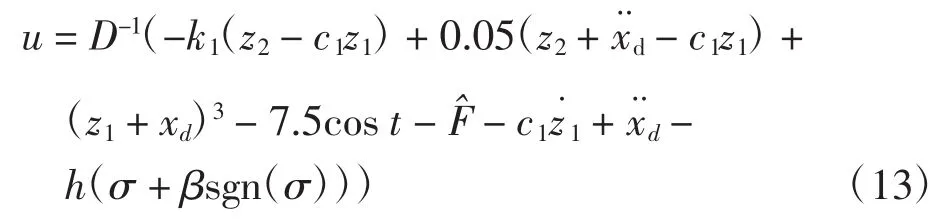
式中：h和β为正的常数。设计自适应率为：

2.3稳定性分析

将式（13）和式（14）代入，得

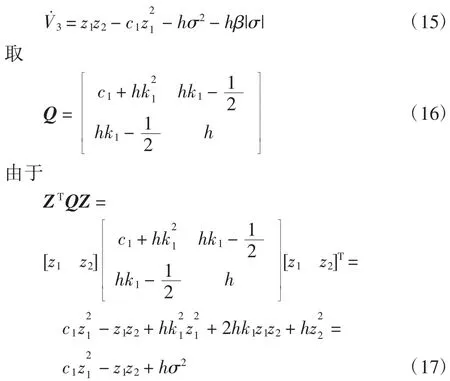
式中：ZT=［z1z2］。

则如果保证Q为正定矩阵，有

由于

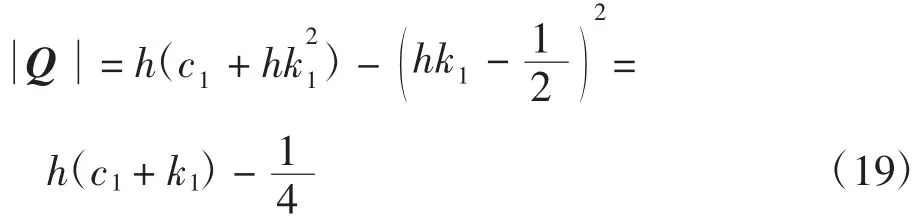
通过取h、c1和k1的值，可使，从而保证Q为正定矩阵，保证。

2.4数值仿真分析

取F=-2sin（0.1 t）、D=1，位置指令xd=sin t、γ=10、c1=20、k1=20、h=40、β=2，将控制输入u加入混沌系统进行数值仿真，仿真结果如图4至图8所示。

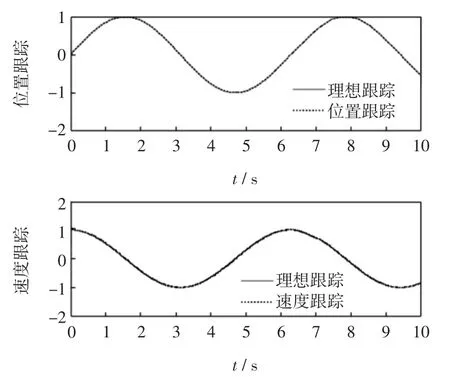
图4　受控系统位置与速度跟踪图

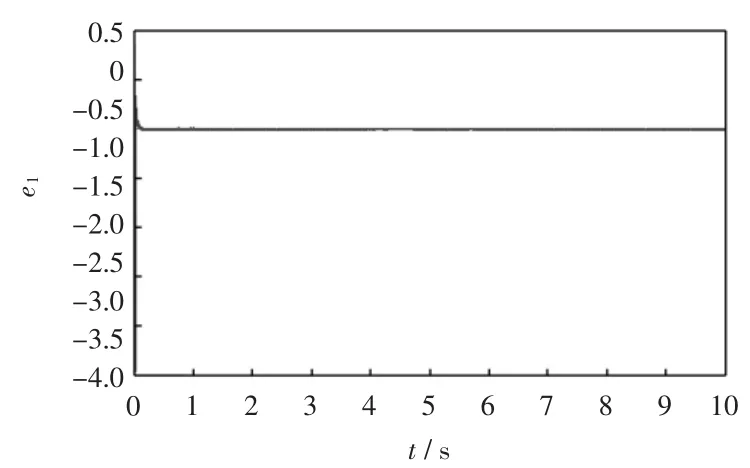
图5　受控系统位置跟踪误差图

图6　速度跟踪误差图

图7　估计曲线

由图4可知，添加控制器后，变量x1和x2迅速脱离混沌态，收敛至预期的位置与速度，并分别按期望的指令稳定运行。由图5和图6可知，受控系统的位置和速度跟踪误差衰减到零，即受控的系统是稳定的。图7说明参数的估计值是稳定的。图8则为系统被控制到稳定的周期-轨道的相图。

图8　受控系统相图

3　结束语

在系统参数不确定和外界干扰的情况下，采用自适应反演滑模方法对上田振子混沌系统进行了控制；运用Matlab数值仿真，将其控制到目标轨道，验证了该控制方法的有效性。

［1］高普云.非线性动力学：分叉、混沌与孤立子［M］.长沙：国防科技大学出版社，2005.

［2］刘秉正，彭建华.非线性动力学［M］.北京：高等教育出版社，2005.

［3］梁翠香.基于状态反馈和自适应方法的混沌控制和反控制［D］.长沙：湖南大学，2011.

［4］刘金琨.滑模变结构控制MATLAB仿真［M］.北京：清华大学出版社，2005.

［5］DAVID YOUNG K.A control engineer’s guide to sliding mode control［J］.IEEE Transaction on Control System Technology，2004（3）：156-164.

［6］OTT E，GREBOGI C，YORKE J A.Controlling chaos［J］. Physical Review Letters，1990，64（3）：1196-1199.

［7］朱凯，齐乃明，秦昌茂.BTT导弹的自适应滑模反演控制设计［J］.宇航学报，2010，31（3）：769-773.

［8］张元涛，石为人，李颍.基于反演的不确定非线性系统自适应滑模控制［J］.华中科技大学学报：自然科学版，2011，39（7）：88-91.

［9］DADRAS S，MOMENI H R.Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17（1）：367-377.

［10］GE S S，WANG C，LEE T H.Adaptive backstepping control of a class of chaotic systems［J］.International Journal of Bifurcation and Chaos，2000，10（5）：1149-1156.

Ueda oscillator chaos control based on adaptive backstepping sliding mode control

LIANG Xiao-wen，ZHAO Xiao-shan，WU Kai-li
（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

For the control problem of uncertain chaotic system，adaptive backstepping sliding mode controller is presented in this paper.The chaos dynamic behavior of the ueda oscillator is analyzed，the adaptive backstepping sliding mode method is used to control the system.Adaptive controller can realize the estimation of the upper bound of the uncertainty of the system，thus enhancing robustness and adaptability of the control system.The simulation results verify the effectiveness of the proposed controller.

chaos control；backstepping sliding mode control；adaptive rate；robustness

TP13；O231

A

2095－0926（2015）04－0054－04

2015-05-18

国家自然科技基金资助项目（11302148）.

梁小文（1989—），女，硕士研究生；赵小山（1967—），男，副教授，硕士生导师，研究方向为非线性动力系统分析.