Heisenberg群上一类半线性方程的Liouville型定理

张书陶，赵　琼，韩亚洲

（中国计量学院理学院，杭州　310018）

Heisenberg群上一类半线性方程的Liouville型定理

张书陶，赵琼，韩亚洲

（中国计量学院理学院，杭州310018）

结合向量场法的思想，研究了Heisenberg群上的一类半线性方程，并给出不存在非平凡正解的Liouville型定理.首先，利用Heisenberg群上左不变向量场的对称性构造一类实泛函，并通过恒等变形获得一些恒等式；然后，利用试验函数的性质，结合Heisenberg群上的极坐标公式、Young不等式等技巧以精确估计，进而证明任一非负解均恒为零.

向量场法；Liouville型定理；半线性方程；Heisenberg群

在Euclidean空间，半线性方程

Heisenberg群的概念来源于量子力学、多复变几何等学科.作为非交换几何的典型代表，学者们对Heisenberg群上的半线性问题

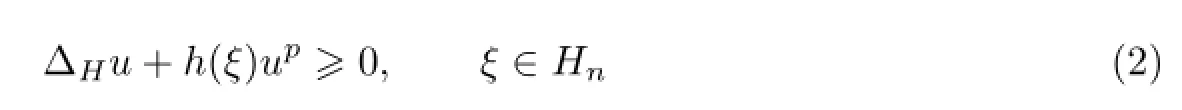
进行了大量的研究［9-11］.为叙述需要，下面首先给出Heisenberg群的一些概念和记号.

Hn上的一个伸缩族为

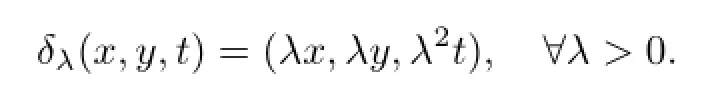
记Q=2n+2为相应的齐次维数.Hn上的一组左不变向量场为

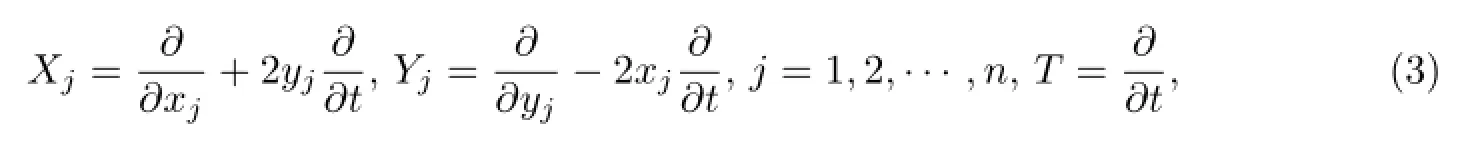
则Xj，Yj，j=1，2，···，n关于伸缩一次齐次，T关于伸缩二次齐次，且

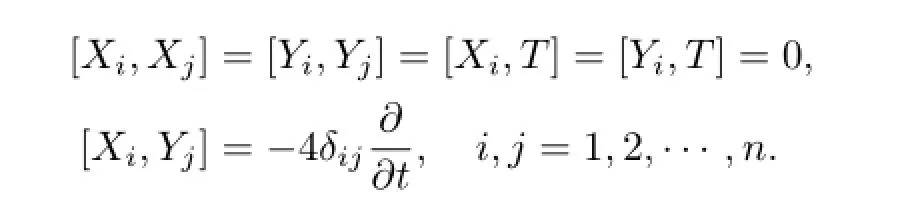
记

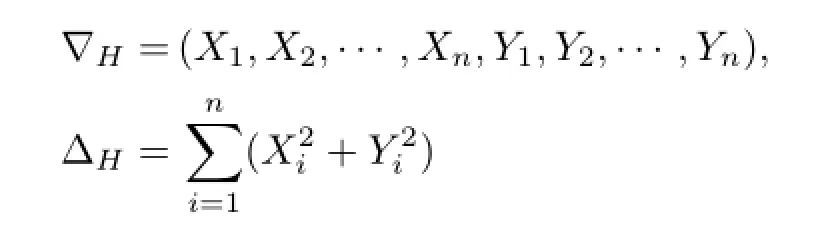
分别为广义梯度和次Laplace算子.定义距离函数为

定理1C2（Hn）表示由Hn上全体二阶连续可微函数组成的集合，令为方程

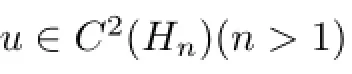
的非负解，其中h（ξ）为Hn上的非负函数且满足

Xu［16］引入的向量场采用了复数的形式，具有较强的对称性，那么对于一些对称性较弱的算子（如左不变向量场（式（3））的推广形式Greiner算子），是否可直接推广呢？本工作结合Xu的思想，采用Heisenberg群上的左不变向量场（式（3）），通过引入一类实泛函从而导出了一些恒等式，并对定理1重新证明.这将为进一步研究以Greiner算子为主部的半线性方程的Liouville性质［12］做充分的准备.

1　有关向量场的积分

令u≥0满足方程（4），并记

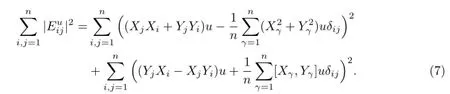
取Ω⊂Hn，（Ω）表示Ω上全体无穷次可微且具有紧支集的函数全体，ϕ∈C∞0（Ω），0≤ϕ≤1，考虑非负积分

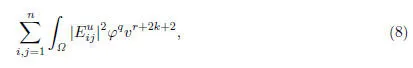
式中，u=v-k（k/=0），q，k，r待定.为书写方便，式（8）及以下积分中均省略积分域Ω和积分微元dxdydt.

由式（7）和（8），可得

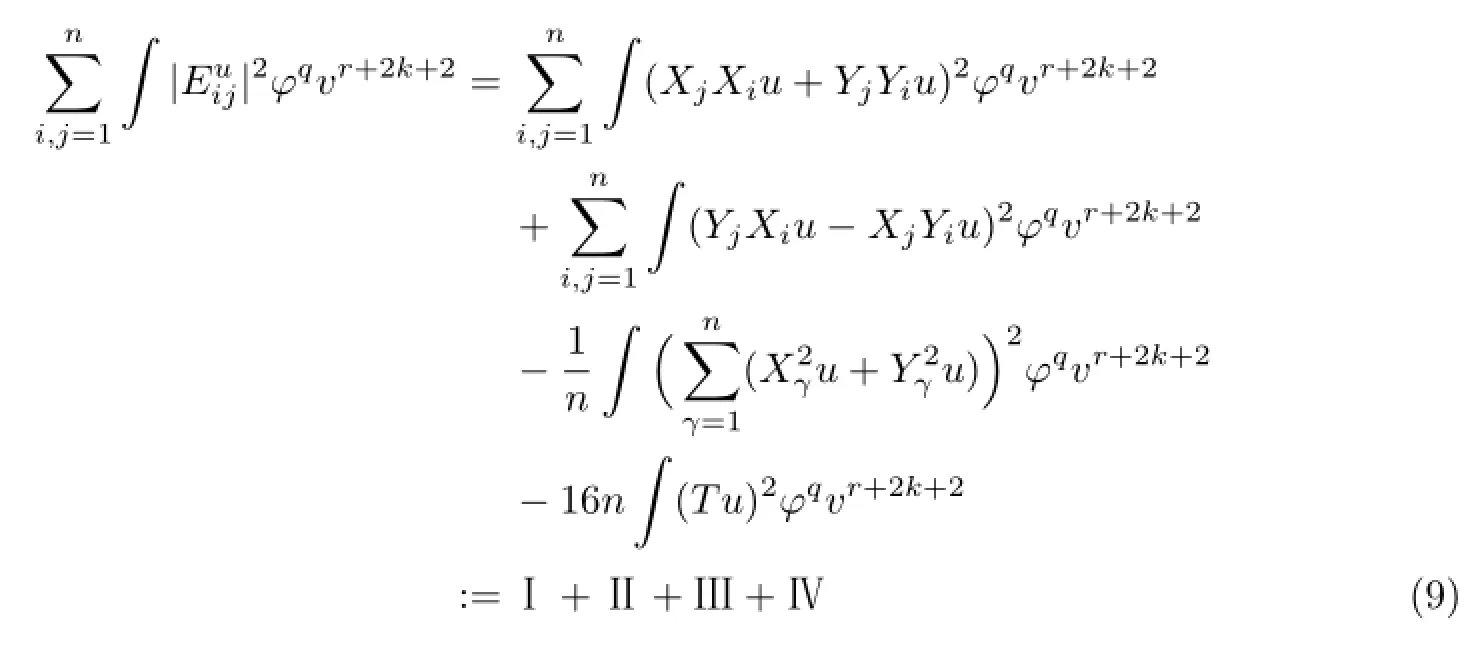
将u=v-k代入式（9），并结合左不变向量场的关系，运用分部积分技巧，经过计算可得

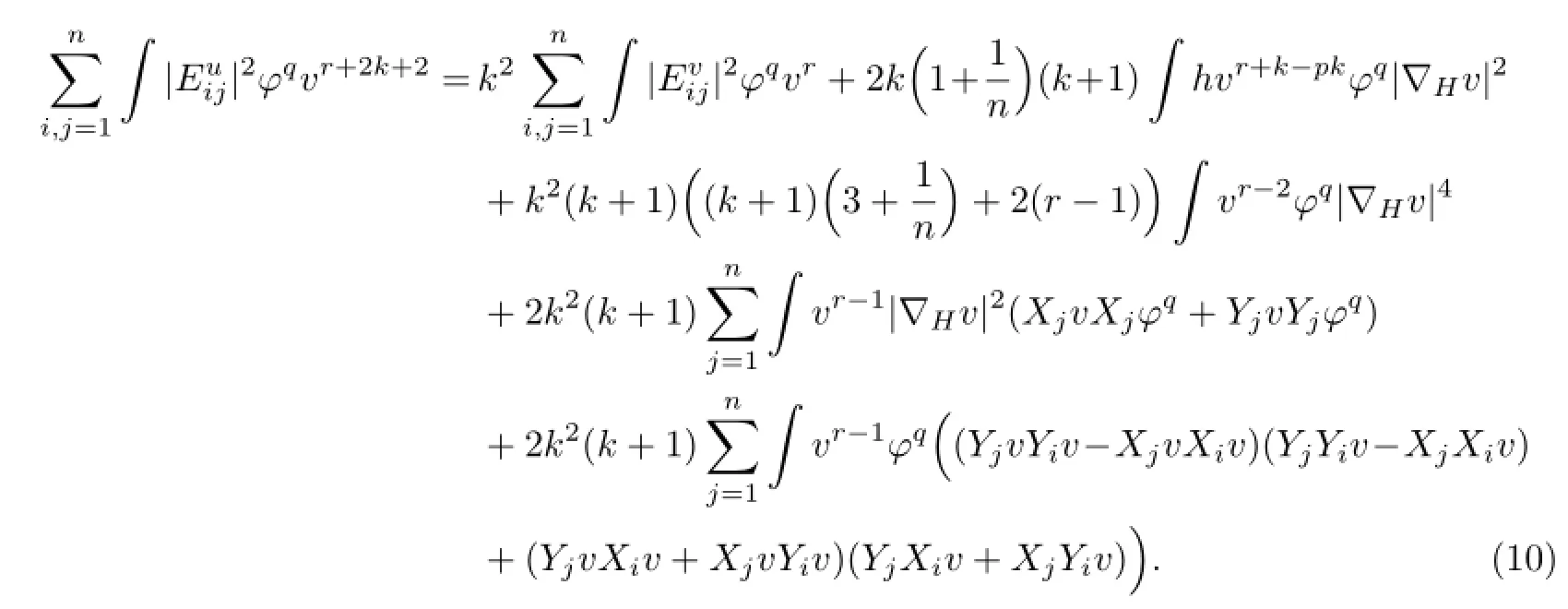
另一方面，注意到

结合左不变向量场的关系，运用分部积分可得

式中，

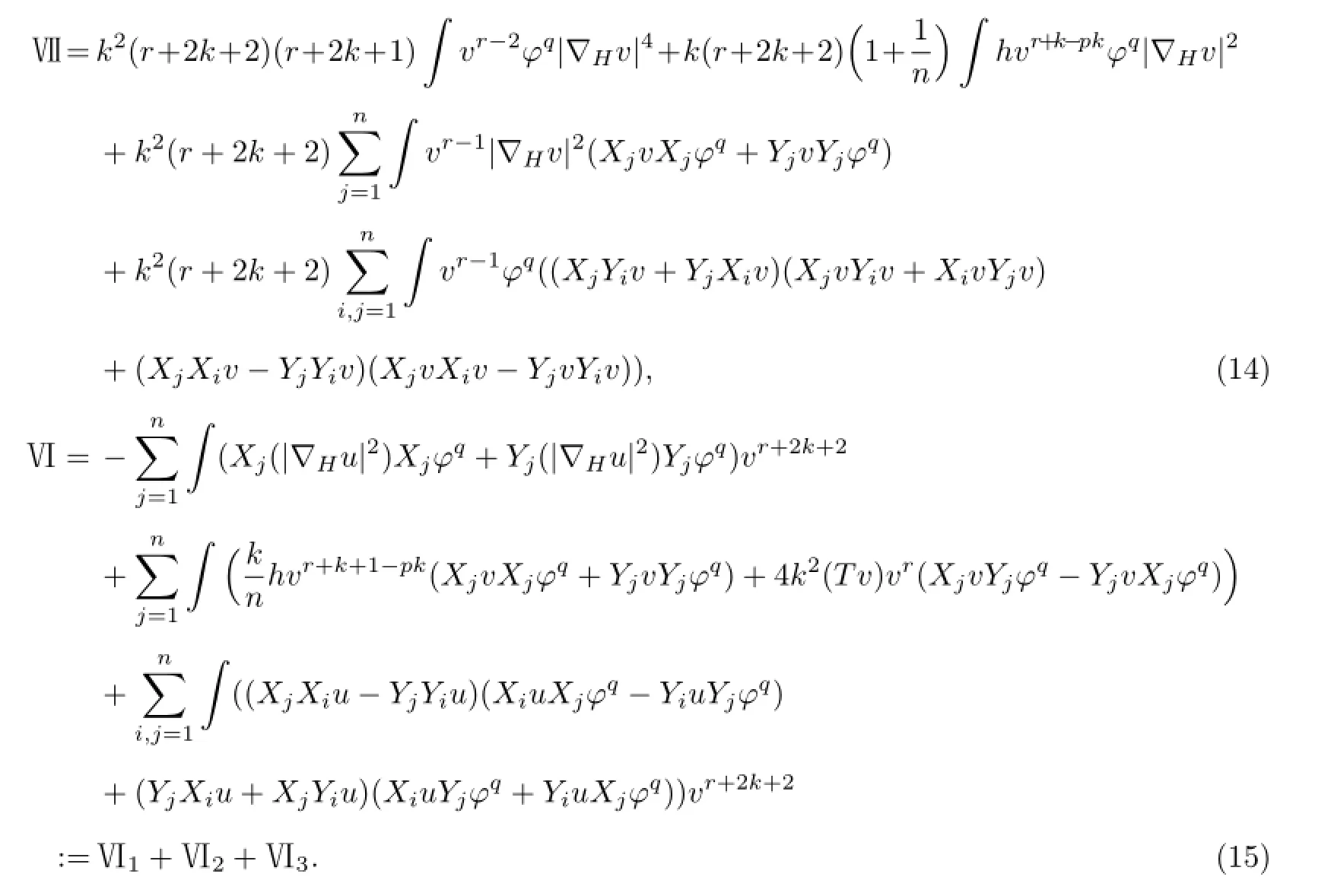
下面对式（15）中的Ⅵ3采用不同的分部积分，分别给出和.一方面，

另一方面，

由式（15）～（17），可得

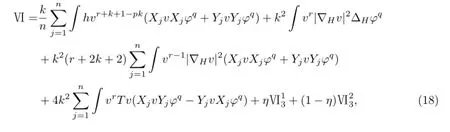
式中，η待定.

2　定理1的证明

由上节的讨论，可得

即有

式中，

首先处理λ5Rhvr+k-pkϕq|∇Hv|2.注意到

另外，通过分部积分有

由式（20）和（21），可得

把式（22）代入到λ5Rhvr+k-pkϕq|∇Hv|2中，则式（19）化为

式中，

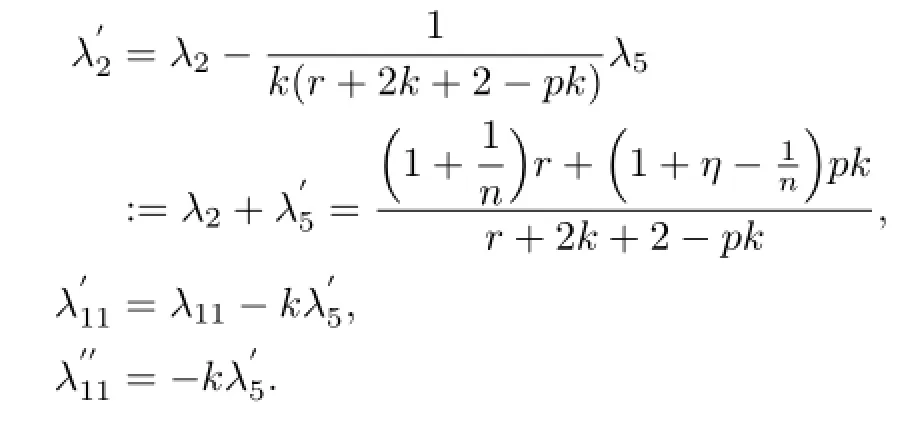
证明（定理1）：选取

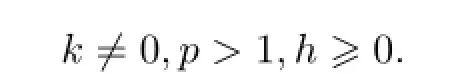
如果由式（23）得到v≡0，则可证u≡0.为使式（23）中“=”号的左边为正，取及 r均非负.由Young不等式

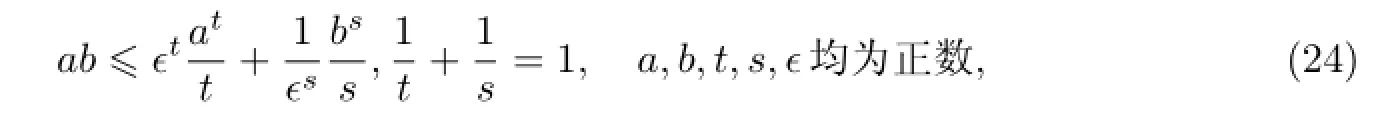
可得

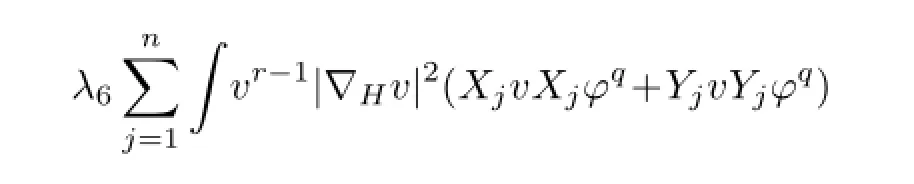
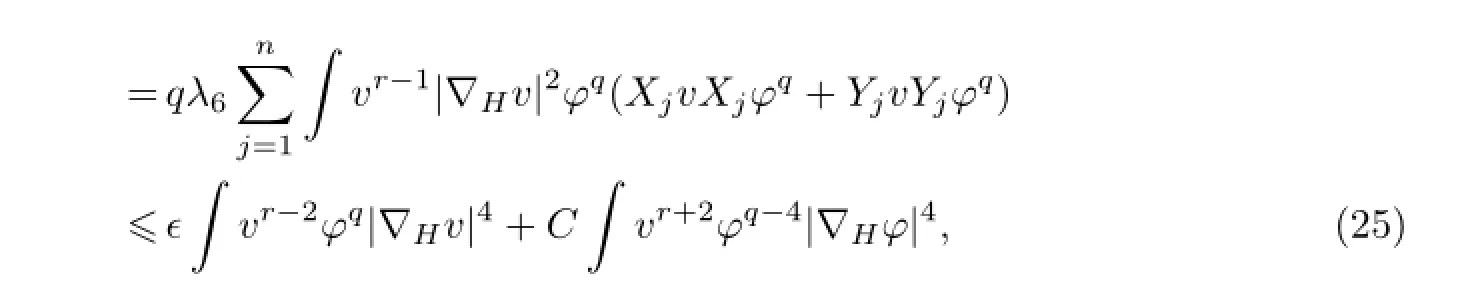
式中，∈为充分小正数，C为某正常数.由ϕ≤1可知，ϕq-1≤ϕq-2，从而有

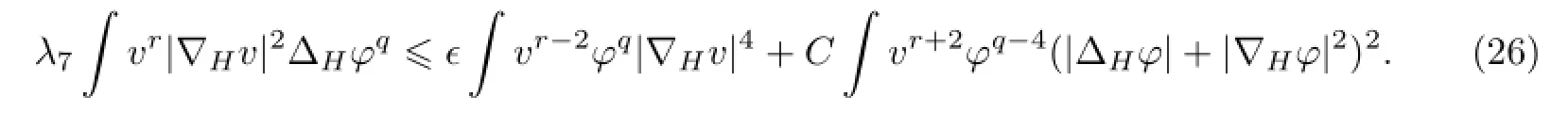
同理可证

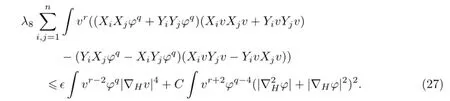
因为λ3≥0，λ4≥0，所以0≤η≤（n-1）/（n+2）.若r=0，则λ1≤0，将无法控制式（26）和（27）中的正项∈Rvr-2ϕq|∇Hv|4，所以r＞0.由λ10=k2r（1-η）可知，λ10/=0，从而有

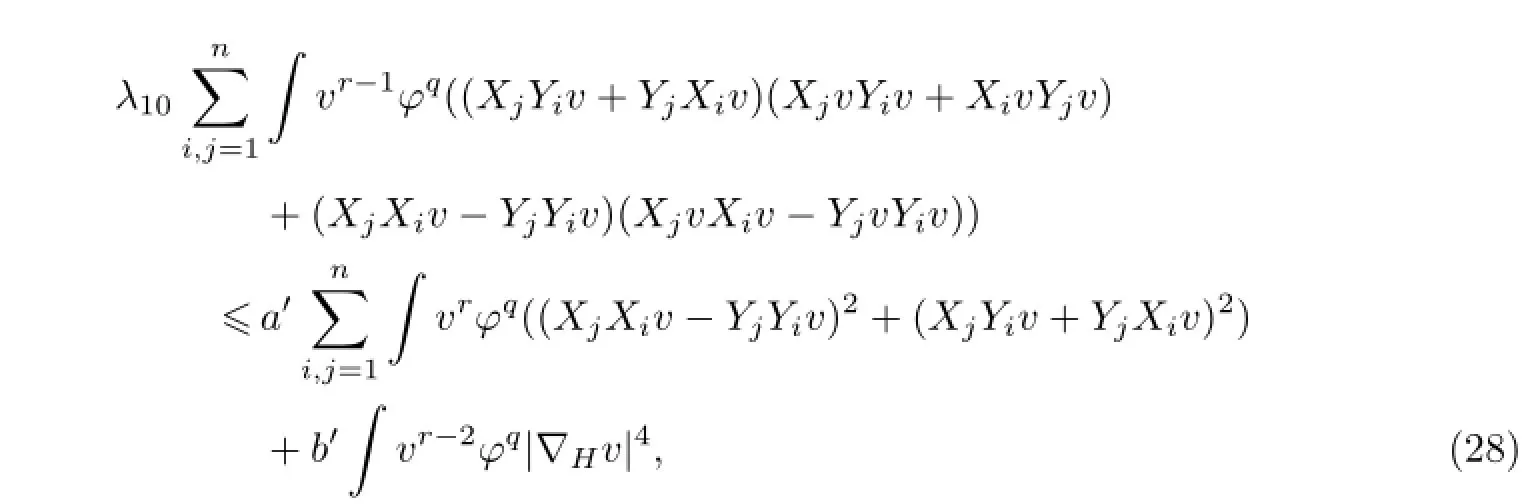
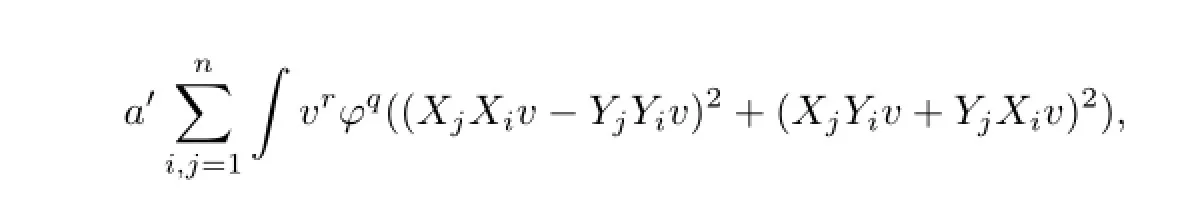
需λ4＞0，从而0＜η≤（n-1）/（n+2）.由λ9/=0可得

为了控制∈Rvrϕq（Tv）2，需要λ3＞0，故0＜η＜（n-1）/（n+2）.

通过分部积分，可得

若

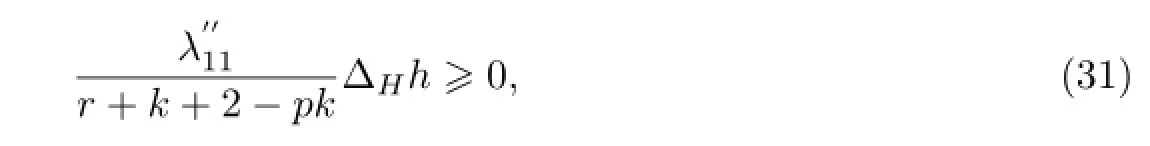
则

故在式（33）成立的情况下，

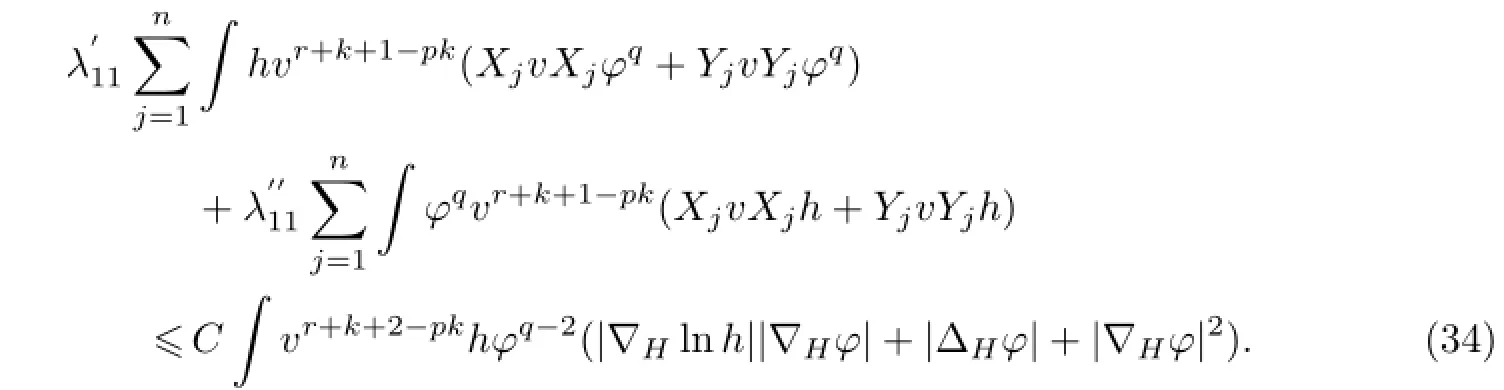
将式（25）～（34）代入式（23），有

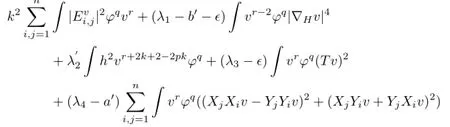
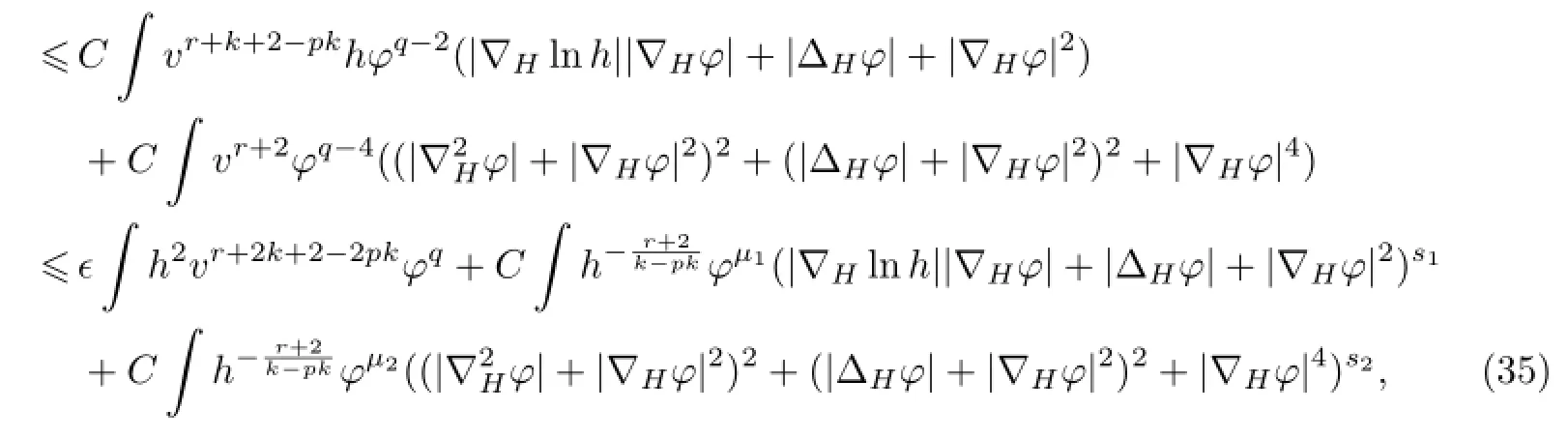
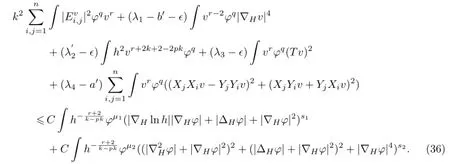
选取Ω=｛ξ∈Hn：|ξ|≤R，R为任一实数｝，ϕ∈（Ω）满足

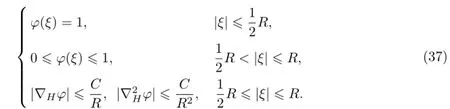
再由式（36）和（38），可得

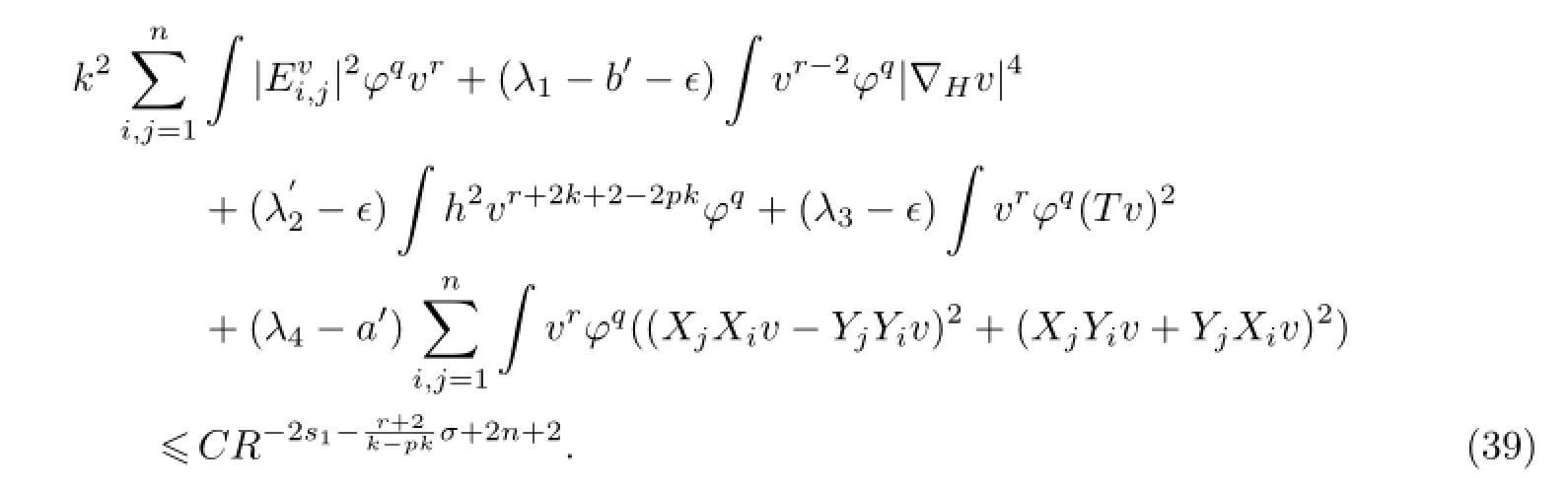
［1］Gidas B，Ni W M，Nirenberg L.Symmetry of positive solutions of nonlinear elliptic equations in Rn［J］.Advances in Mathematics Supplementary Studies，1981，7A：369-402.

［2］Caffarelli L，Gidas B，Spruck J.Asymptotic symmetry and local behavior of semilinear elliptic equations with critical Sobolev growth［J］.Communications on Pure and Applied Mathematics，1989，42：271-297.

［3］Chen W，Li C.Classification of solutions of some nonlinear elliptic equations［J］.Duke Mathematical Journal，1991，63：615-622.

［4］Chen W，Li C，OU B.Classification of solutions for an integral equation［J］.Communications on Pure and Applied Mathematics，2006，59：330-343.

［5］Li C.Local asymptotic symmetry of singular solutions to nonlinear elliptic equations［J］.Inventiones Mathematicae，1996，123：221-231.

［6］Gidas B，Spruck J.Global and local behavior of positive solutions of nonlinear elliptic equations［J］.Communications on Pure and Applied Mathematics，1981，85：525-598.

［7］Obata M.The conjecture on conformal transformations of Riemannian manifolds［J］.Journal of Differential Geometry，1971，6：247-258.

［8］Chang S Y A，Gursky M J，Yang P C.Entire solutions of a fully nonlinear equation［M］// Lectures on partial differential equations.Boston：International Press，2003：43-60.

［9］Birindelli I，Dolcetta I C，Cutri A.Liouville theorems for semilinear equations on the Heisenberg groups［J］.Annales de l'Institut Henri Poincare，1997，14（3）：295-308.

［10］Birindelli I，Dolcetta I C，Cutri A.Indefinite semi-linear equations on the Heisenberg group：a priori bounds and existence［J］.Comm Partial Differential Equations，1998，23：1123-1157.

［11］Birindelli I，Prajapat J.Nonlinear Liouville theorems in the Heisenberg group via the moving plane method［J］.Comm Partial Differential Equations，1999，24（9/10）：1875-1890.

［12］Han Y Z，Zhao Q，Jin Y Y.Semi-linear Liouville theorem in the generalized Greiner vector fields［J］.Indian Journal of Pure and Applied Mathematics，2013，44（3）：311-342.

［13］Jerison D S，Lee J M.The Yamabe problem on CR manifolds［J］.Journal of Differential Geometry，1987，25（2）：167-197.

［14］Jerison D S，Lee J M.Extremals for the Sobolev inequality on the Heisenberg group and Yamabe problem［J］.J Amer Math Soc，1988，1（1）：1-13.

［15］Garofalo N，Vassilev D.Symmetry properties of positive entire solutions of Yamabe type equations on the groups of Heisenberg type［J］.Duke Mathematical Journal，2001，106：411-448.

［16］Xu L.Semi-linear Liouville theorems in the Heisenberg group via vector field methods［J］. Journal of Differential Equations，2009，247（10）：2799-2820.

A Liouville type theorem of semi-linear equations on the Heisenberg group

ZHANG Shu-tao，ZHAO Qiong，HAN Ya-zhou
（College of Sciences，China Jiliang University，Hangzhou 310018，China）

Referring to the method of vector fields，this paper studies a class of semilinear equations on the Heisenberg group and gives a Liouville type theorem，namely，the nonexistence of nontrivial positive solutions.A class of real functional constituted by leftinvariant vector fields on the Heisenberg group is introduced.Some identities are obtained by identical deformation.It is proved that any nonnegative solution is trivial according to the properties of test function and some techniques such as polar coordinates formula on the Heisenberg group and Young inequality.

vector field method；Liouville type theorem；semi-linear equation；Heisenberg group

O 175.2

A

1007-2861（2015）03-0319-12

10.3969/j.issn.1007-2861.2013.07.052

2013-10-29

国家自然科学基金资助项目（11201443）；浙江省自然科学基金资助项目（Y6110118）

韩亚洲（1978—），男，副教授，博士，研究方向为椭圆方程的定性理论.E-mail：yazhou.han@gmail.com