二阶精度混合Legendre-球面调和拟谱方法求解Fisher型方程

邓红梅，黄　伟

（上海大学理学院，上海　200444）

二阶精度混合Legendre-球面调和拟谱方法求解Fisher型方程

邓红梅，黄伟

（上海大学理学院，上海200444）

提出了求解两同心球所介区域上Fisher型方程的时间方向二阶精度的混合Legendre-球面调和拟谱格式.该格式在半径方向选择Gauss型的Legendre插值逼近，球面方向选择球面调和插值逼近，而时间方向的导数采用二阶中心差商离散.数值结果显示，该算法具有较好的稳定性和较高精度.

Legendre-球面调和拟谱方法；Fisher型方程；时间方向二阶精度；两同心球所介区域

O 241.82

A

1007-2861（2015）03-0331-05

本工作的研究背景主要是气象科学和天体物理学等实际问题，这些问题通常可以归结为求解球内或两同心球所介区域上的偏微分方程初边值问题［1-2］.最初，谱方法和拟谱方法大多研究周期问题和矩形区域上的问题.20世纪90年代，Guo等［3-5］发展了以球面调和函数为基函数的球面正交逼近和插值逼近，并将球面调和谱方法和拟谱方法应用于研究球面上的涡度方程和流体低马赫数流动.该研究为其他形式的球形区域上的谱方法和拟谱方法奠定了基础.此后，Guo等［6-8］又采用混合Jacobi-球面调和谱和拟谱方法求解了单位球内偏微分方程初边值问题.近期，夏文杰等［9］提出了采用时间方向一阶精度的混合Legendre-球面调和谱格式求解两同心球所介区域上的Fisher型方程.若从实际计算的角度考虑，拟谱方法在保证高精度的同时，算法更加简便，计算量也有所减少.因此，本工作的目的是应用混合Legendre-球面调和拟谱方法求解两同心球所介区域上的Fisher型方程.

考虑到同心球所介区域的特点，选择球面坐标表示空间位置，并将空间坐标分为半径方向和球面方向.若r，λ和θ分别表示半径、经度和纬度，并令Ω=I×S，其中，则本工作所考虑的模型问题可表示为

式中，U为反应浓度，ν是扩散系数，g（r，λ，θ，t）和U0（r，λ，θ，t）为已知函数.根据球面坐标下的空间自变量可分解为半径和球面两个方向的特点，时间方向二阶精度的混合Legendre-球面调和拟谱格式在半径方向的区间I上选择经过变换的Gauss型插值，在球面S上选择球面调和插值，而在时间方向上利用二阶精度的中心差商代替微商.数值结果表明，上述算法效果较好.

1　全离散混合拟谱格式

为了方便格式的描述，首先引入一些必要的记号.

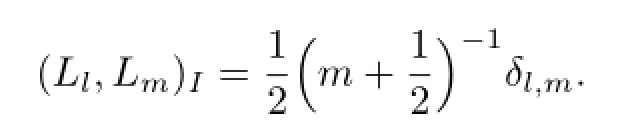
若记关联Legendre函数

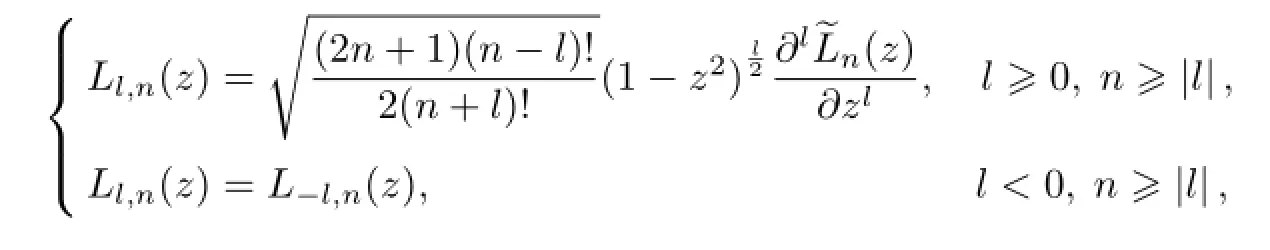
那么球面调和函数定义为

令M和N是非负整数，PM（I）表示所有次数不超过M的代数多项式在I上的限制所组成的集合.特别地，又记则表示由中所有实值函数组成的集合，选择f

作为逼近子空间.

现记rG，M，i为LM+1（r）的零点，ωG，M，i为相应的Christoffel数（0≤i≤M），在I上定义离散内积

记zN，k为的零点，ωN，k为相应的Christoffel数（0≤k≤N）.选择球面S上的插值点集e

相应地，球面S上的离散内积定义为

式中，v∗表示v的共轭.根据文献［3］中的结论，对任意u，v∈WN（S），有

成立，式中，

因此，｛Yl，n||l|≤n≤N｝关于（·，·）N，S正交.

将上述定义在I和S上的离散内积相结合，构成Ω上的离散内积如下：

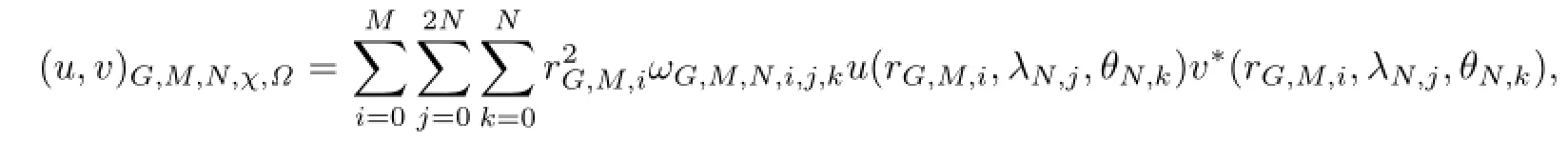
成立，式中，

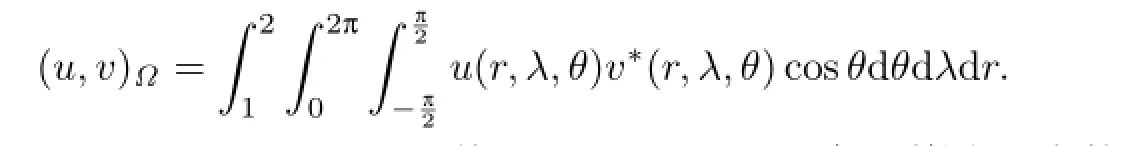
下面引入格式.令τ为时间t方向的网格步长，

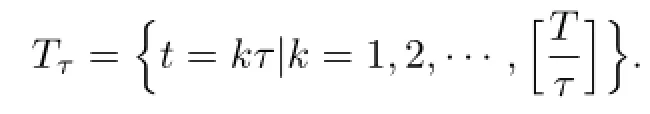
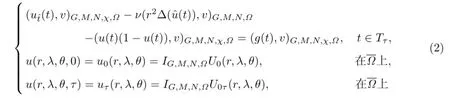
成立，式中，

考虑到格式的特性，将u（t）表示为

2　数值算例

取试验函数

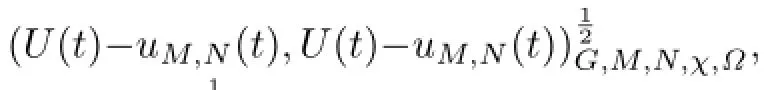
图1为ν=1，τ=τj（j=1，2，3）时在t=1处的平均绝对数值误差和平均相对数值误差随M（M=N）的变化，其中τ1=5.0×10-2，τ2=5.0×10-3，τ3=5.0×10-4.由图1可以看出，当M比较小时，采用本研究提出的算法仍能计算出精度较高的数值解，且随着M的增大及τ的减小，误差快速递减.

图1　t=1时试验函数的2种数值误差Fig.1 Two numerical errors at t=1

图2为0＜t≤10，ν=1，τ=τ3时不同M=N下的平均绝对数值误差和平均相对数值误差.图2的结果表明，本研究提出的格式相当稳定.

3　结束语

本研究中，我们利用混合法的思想，提出了求解2个同心球所介区域上的Fisher型方程的时间方向二阶精度混合Legendre-球面调和拟谱格式.数值结果表明，该算法具有较好的稳定性和较高的精度.本研究中的方法也可应用于其他球型区域上的问题.

图2　试验函数的2种数值误差（0＜t≤10）Fig.2 Two numerical errors between t=1 and t=10

［1］Haltiner G J，Williams R T.Numerical prediction and dynamical meteorology［M］.New York：Wiley，1980.

［2］Williamson D L，Drake J B，Hack J J，et al.A standard test set for numerical approximations to the shallow water equations in spherical geometry［J］.Journal of Computational Physics.1992，102：211-224.

［3］Cao W M，Guo B Y.A pseudospectral method for vorticity equations on spherical surface［J］. Acta Mathematicae Applicatae Sinica：English Series，1997，13（2）：176-187.

［4］Guo B Y.A spectral method for vorticity equations on spherical surface［J］.Applied Mathematics and Computation，1995，64：1067-1079.

［5］Guo B Y，Cao W M.A spectral method for the fluid flow with low Mach number on spherical surface［J］.Journal on Numerical Analysis，1995，32：1764-1777.

［6］Guo B Y，Wang L L.Jacobi interpolation approximations and their applications to singular differential equations［J］.Advances in Computational Mathematics，2001，14：227-276.

［7］Guo B Y.Jacobi approximations in certain Hilbert spaces and their applications to singular differential equations［J］.Journal of Mathematical Analysis and Applications，2000，243（2）：373-408.

［8］Guo B Y，Wang L L.Jacobi interpolation approximations in non-uniformly Jacobi-weighted Sobolev spaces［J］.Journal of Approximation Theory，2004，128（1）：1-41.

［9］夏文杰，黄伟.求解Fisher型方程的混合Legendre-球面调和谱方法［J］.应用数学与计算数学学报，2014，28（1）：26-32.

［10］Bernardi C，Maday Y.Handbook of numerical analysis：spectral methods［J］.Techniques of Scientific Computing，1997，5：209-485.

［11］Guo B Y，Huang W.Mixed Jacobi-spherical harmonic spectral method for Navier-Stokes equations［J］.Applied Numerical Mathematics，2007，57：939-961.

［12］黄伟，郭本瑜.Navier-Stokes方程的全离散Jacobi-球面调和谱方法［J］.应用数学和力学，2008，29（4）：409-431.

A second order accurate mixed legendre-spherical harmonic pseudo-spectral method for the Fisher equation

DENG Hong-mei，HUANG Wei
（College of Sciences，Shanghai University，Shanghai 200444，China）

The paper proposes a second mixed Legendre-spherical harmonic pseudospectral scheme for the Fisher equation in a domain between two concentric balls.Legendre interpolation is used in the radial direction，and spherical harmonic interpolation in other directions.The second order central difference quotient is used for time derivatives.Numerical results show high accuracy of the proposed algorithm.

mixed Legendre-spherical harmonic spectral method；Fisher equation；second order accurate in the temporal direction；domain between two concentric balls

10.3969/j.issn.1007-2861.2014.01.038

2013-12-16

国家自然科学基金资助项目（11372170，11176015）；上海市重点学科建设资助项目（J50101）

黄伟（1960—），男，副教授，研究方向为偏微分方程的谱方法.E-mail：weihuang@mail.shu.edu.cn