一类具有年龄结构的SIRS模型的全局稳定性

张仲华，锁要红

（西安科技大学理学院，西安　710054）

一类具有年龄结构的SIRS模型的全局稳定性

张仲华，锁要红

（西安科技大学理学院，西安710054）

建立了一类具有隔离措施及年龄结构的SIRS传染病（免疫期有限的传染病）模型，定义了疾病的基本再生数，并通过构造Lyapunov函数讨论了模型的平衡点的全局渐近稳定性.

染病年龄；SIRS传染病模型；全局渐近稳定性

具有染病年龄结构的传染病模型因为能更准确地刻画一些疾病（如性病等）传播的实际情况，所以近年来受到了广大数学工作者的广泛关注，并成为了应用数学领域的一个新的研究热点［1-11］.然而由于年龄结构的引入，传染病模型表现为偏微分方程（partial differential equation，PDE）与常微分方程（ordinary differential equation，ODE）相结合，即具有微分-积分结构的数学模型.由于这类数学模型的结构复杂，传统的构造Lyapunov函数的方法无法研究模型平衡点（特别是地方病平衡点）的全局渐近稳定性.已有的研究工作对这类模型的地方病平衡点的全局渐近稳定性也鲜见涉及.Thieme等［4］建立了一类具有饱和接触率及染病年龄结构的艾滋病传播SIA模型，并运用特征值方法及Laplace变换等讨论了地方病平衡点的渐近稳定性.Kim等［5］将一般的非线性光滑函数及染病年龄结构引入传统的SIR模型，并讨论了模型非负解的存在唯一性.后来，Kim［6］又给出了传统的SIR模型的地方病平衡点指数渐近稳定的一般性条件.另外，Zhang等［10］研究了一类具有一般饱和接触率的SIRS模型（免疫期有限的传染病模型）的非负解的存在唯一性以及地方病平衡点的指数渐近稳定性.本工作在假设种群的接触率及隔离率均为种群规模的线性函数的基础上建立了一类SIRS模型，并通过构造合适的Lyapunov函数系统地研究了模型局部及全局渐近稳定性等动力学性态.

1　模型的建立

Mena-Lorca和Hethcote在文献［12］中将整个人群分为S（易感）、I（感染）和R（免疫）3类，并建立了如下模型：

式中，S（t），I（t）和R（t）分别为t时刻易感者、感染者及免疫者的数量，Λ为人口的输入率，β为传染率，δ为免疫失去率，µ为自然死亡率，α为因病死亡率，γ为治愈率.Mena-Lorca和Hethcote证明了模型（1）地方病平衡点在δ=0时的全局渐近稳定性［12］.

本工作在模型（1）的基础上，通过引入染病年龄建立如下SIRS模型：

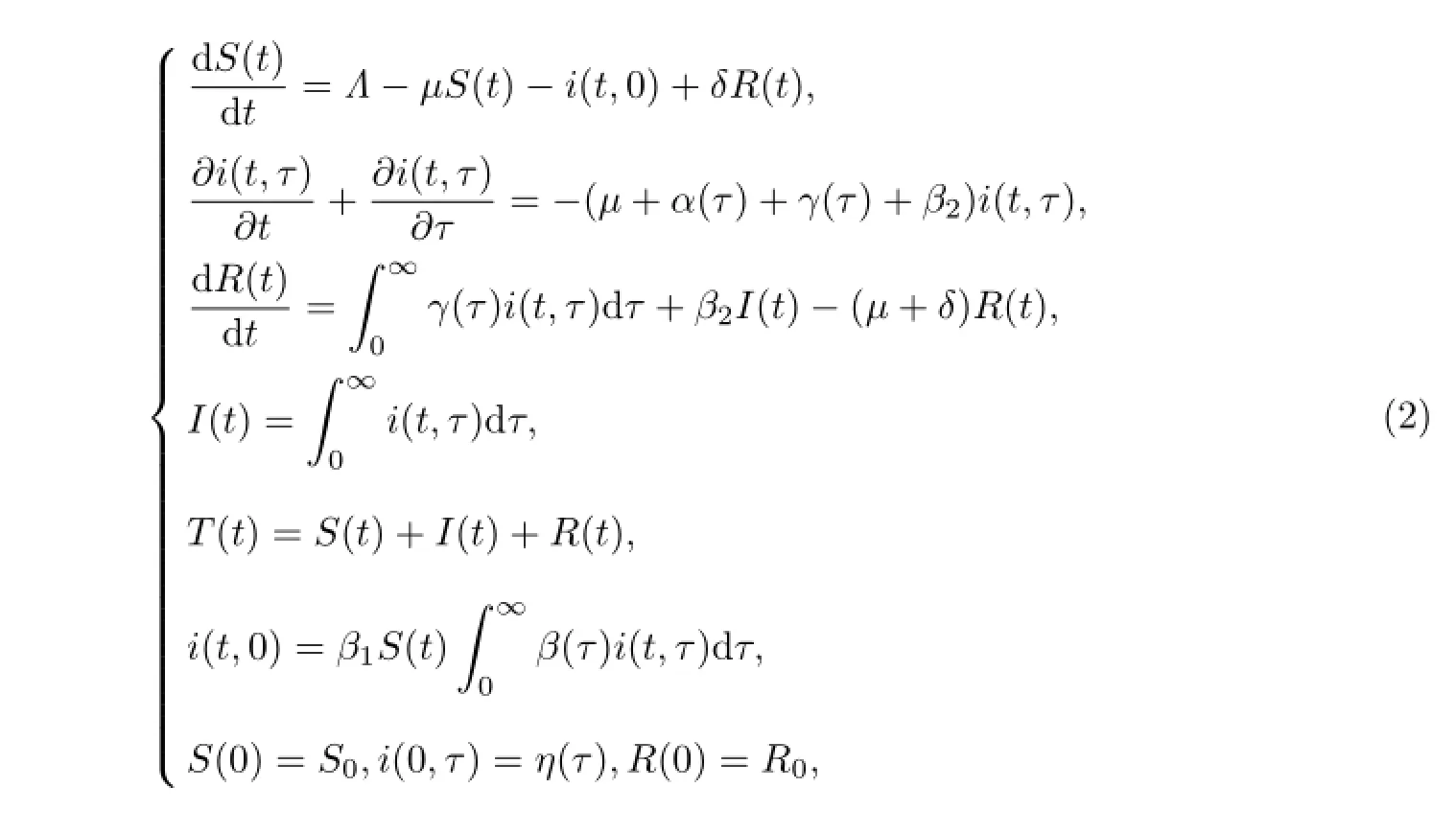
式中，i（t，τ）为t时刻染病年龄为τ的感染者的数量，γ（τ），β（τ）分别为染病年龄为τ的感染者的治愈率和传染率，β1，β2分别为接触率（β1T（t））和隔离率（β2T（t））的系数.

由文献［10］中给出的方法可证，对于非负初值S0≥0，η（τ）≥0，R0≥0，模型（2）存在唯一的全局非负解.将模型（2）中的第2式关于τ积分，并结合第1，3，4式，可得

2　平衡点的存在性

设（S，i（τ），R）为模型（2）的平衡点，则其满足如下微分-积分方程组：

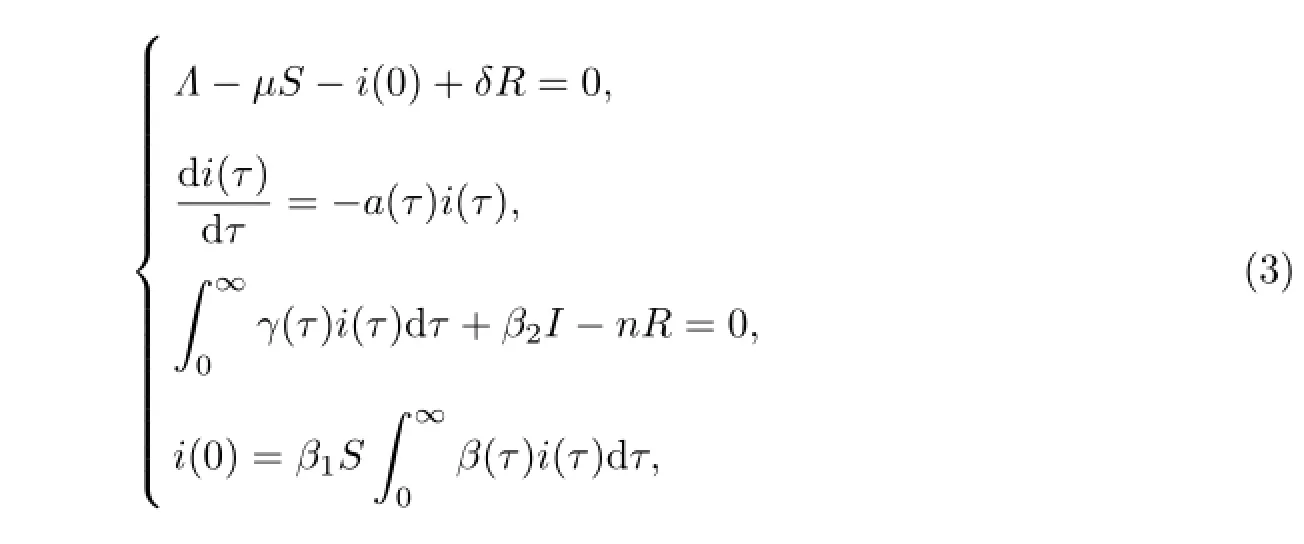
为讨论方便，引入如下记号：

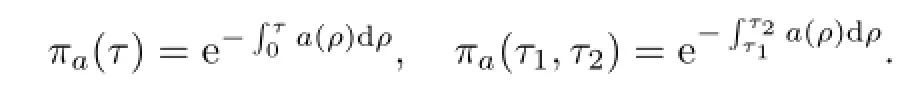
疾病的基本再生数定义为

式中，πa（τ）为一个病人能够活过年龄τ的概率表示一个病人在整个染病期的感染力.因此，R0表示一个典型的感染者被引入的种群时在其整个染病期内所制造的二次感染数.

定理1当R0≤1时，模型（2）仅存在无病平衡点时，模型（2）除存在无病平衡点外，还有唯一的地方病平衡点其中

证明由式（3）中的第2式，可得i（τ）=i（0）πa（τ），则i（τ）≥0，当且仅当i（0）=0时等号成立.

当i（τ）＞0时，由式（3）中的第1，3式，可得

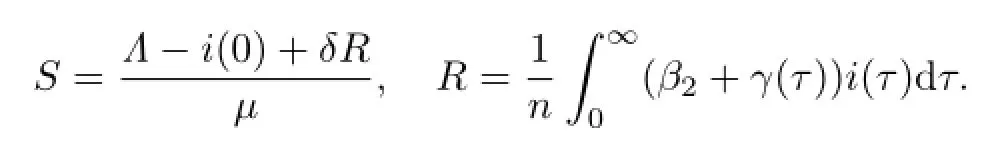
将上述第2式代入式（3）中的第4式，可得

3　无病平衡点的稳定性

首先讨论无病平衡点的局部渐近稳定性.

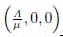
将式（5）中的第2式关于τ积分，可得

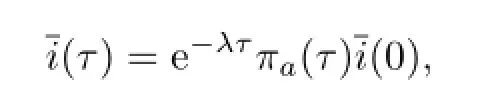
从而可求得特征方程

令λ=x+iy，其中i为虚数单位，分离式（6）的实部、虚部，可得

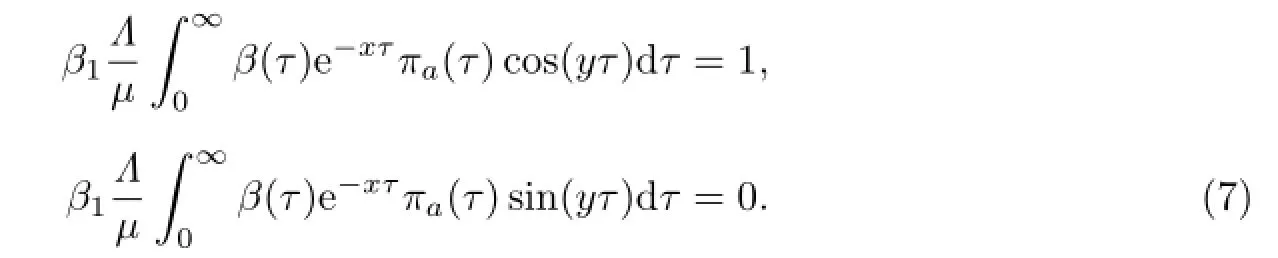
当x≥0时，由式（7）可得

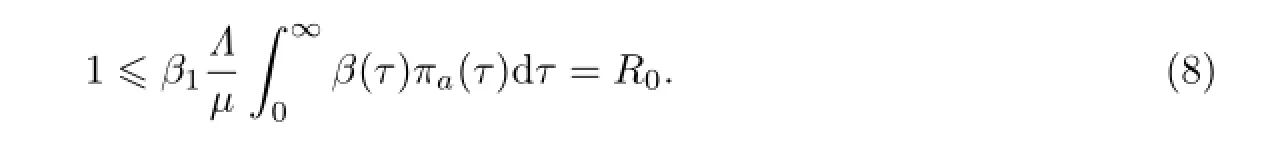
显然，式（8）与定理的条件矛盾.因此，当R0＜1时，式（6）不具有非负实部的解.

因此，当R0＜1时，无病平衡点0，0）局部渐近稳定.

定理3当R0≤（µ+α（τ））πa（τ）dτ时，无病平衡点（，0，0）全局渐近稳定.

证明构造如下Lyapunov函数：

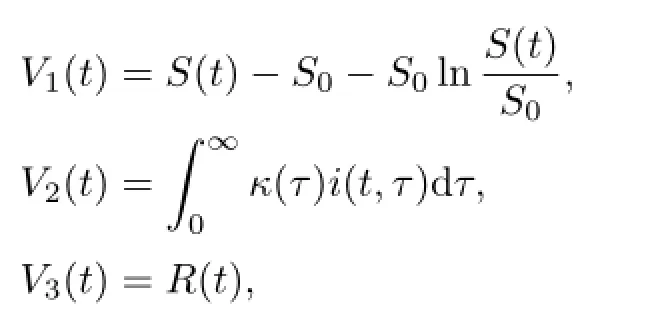
式中，S0=，κ（τ）为待定的函数.函数V1（t），V2（t），V3（t）的全导数分别为

令V4（t）=V2（t）+V3（t），则有

因此，

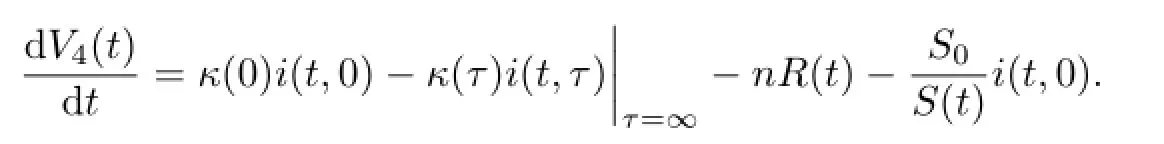
令V=V1（t）+V4（t），则有

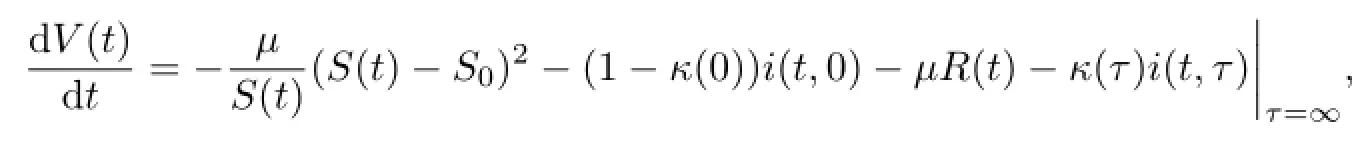
因此，当R0≤（µ+α（τ））πa（τ）dτ时，无病平衡点（，0，0）全局渐近稳定.

4　地方病平衡点的稳定性

由文献［10］中给出的方法不难得到：当R0＞1时，地方病平衡点（S∗，I∗，R∗）局部渐近稳定.下面讨论当R0＞1时地方病平衡点（S∗，I∗，R∗）的全局渐近稳定性.

定理4当R0＞1，δ=0时，地方病平衡点（S∗，I∗，R∗）全局渐近稳定.

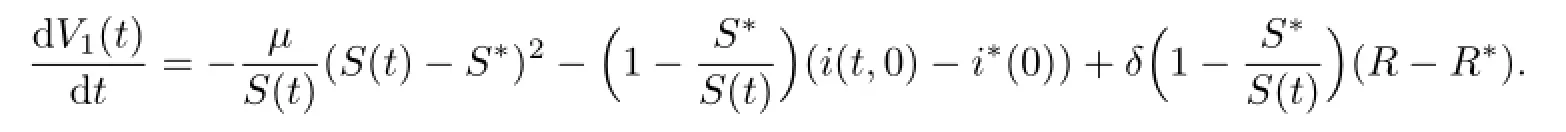
将式（2）中的第2式沿特征线t=τ+c积分，可得

将式（9）代入V2（t），则函数V2（t）可转化为

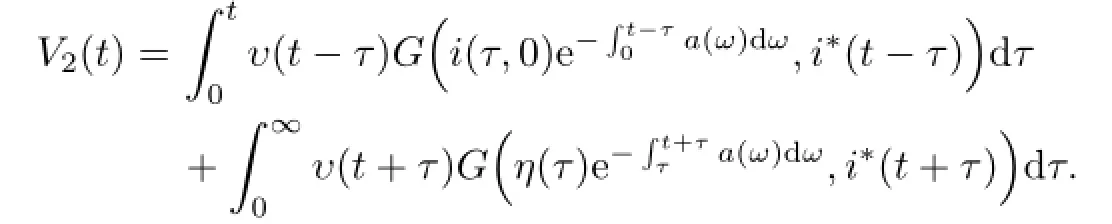
函数V2（t）的全导数为

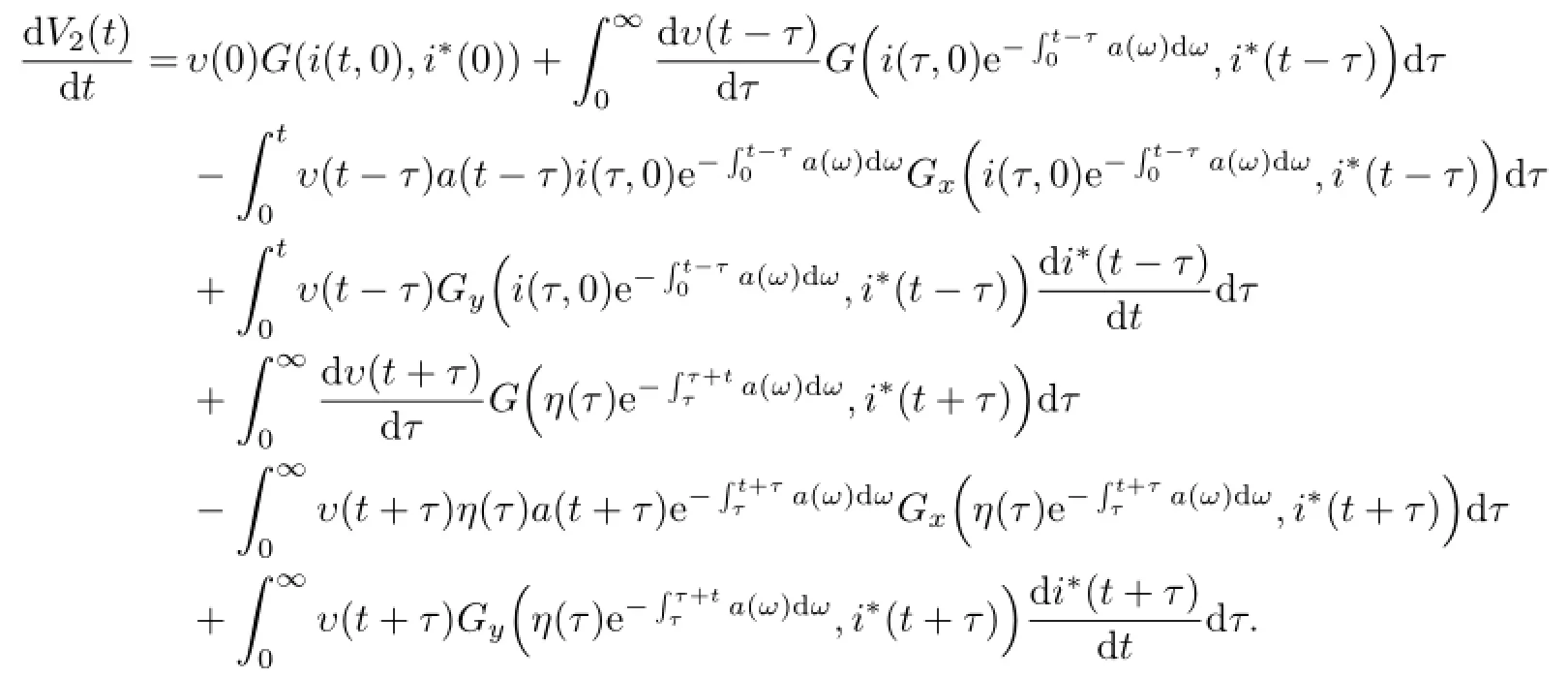
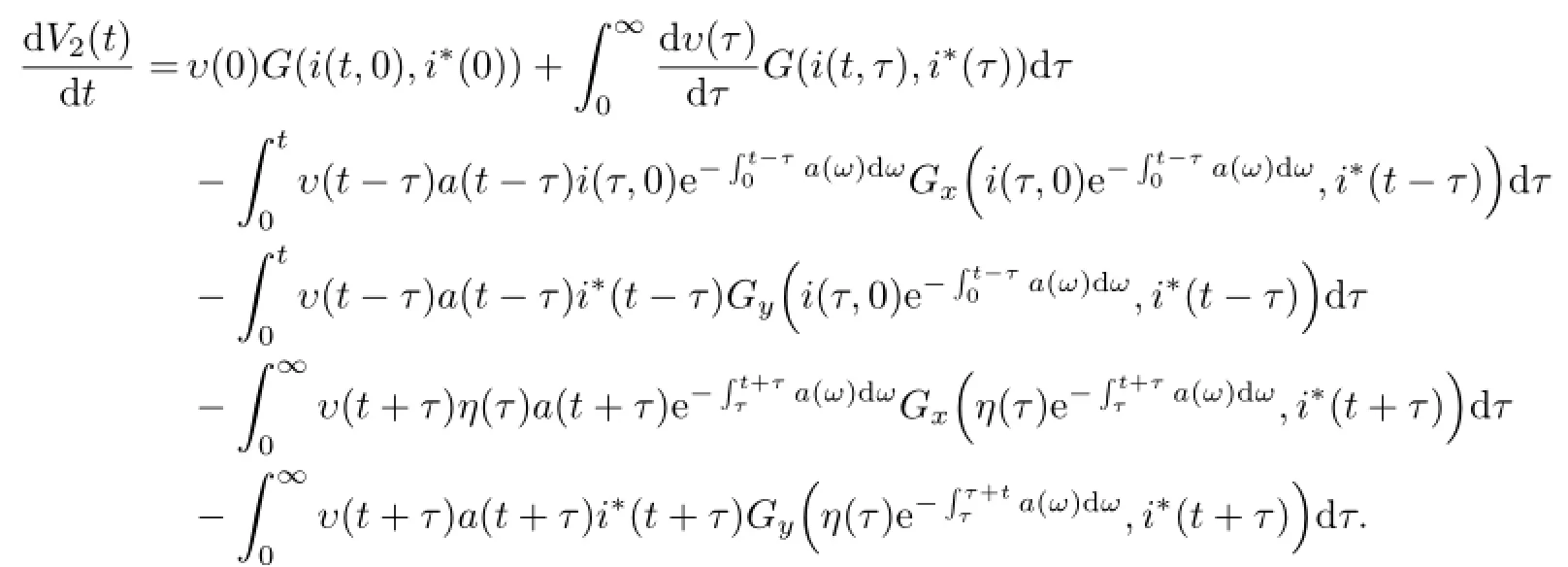
令V（t）=V1（t）+V2（t），则有

当δ=0时，式（2）中关于S（t）和i（t，τ）的方程及其定解条件构成一个独立的子系统，由Lyapunov稳定性理论可得

另外，由式（2）中的第3式可得

因为

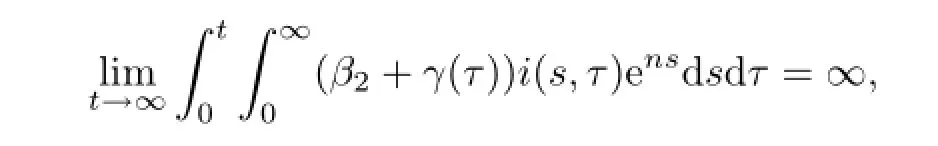
所以，由洛必达法则可得

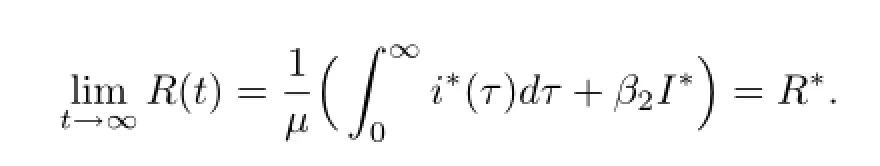
因此，当R0＞1，δ=0时，地方病平衡点（S∗，I∗，R∗）全局渐近稳定.

5　结束语

本工作建立了一类具有染病年龄结构及隔离措施的SIRS传染病模型，该模型是由常微分方程与偏微分方程相结合生成的微分-积分模型.这类传染病模型的平衡点（特别是地方病平衡点）的稳定性一直是应用数学领域的一个研究热点及难点.

本工作首先定义疾病的基本再生数，然后通过分析特征方程解的分布情况及构造恰当的Lyapunov函数，讨论了由基本再生数R0决定的模型无病平衡点及地方病平衡点的稳定性，最后得到了平衡点全局渐近稳定的充分条件.

［1］Song J，Yu J Y.Population system control［M］.Berlin：Springer-Verlag，1987.

［2］陆征一，周义仓.数学生物学进展［M］.北京：科学出版社，2006.

［3］马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究［M］.北京：科学出版社，2004.

［4］Thieme H R，Castillo-Chavez C.How may infection-age-dependent infectivity affect the dynamics of HIV/AIDS？［J］.SIAM Journal on Applied Mathematics，1993，53（5）：1447-1479.

［5］Kim M Y，Milner F A.A mathematical model of epidemics with screening and variable infectivity［J］.Mathematical and Computer Modelling，1995，21（7）：29-42.

［6］Kim M Y.Existence of steady state solutions to an epidemic model with screening and their asymptotic stability［J］.Applied Mathematics and Computation，1996，74（1）：37-58.

［7］Kribs-Zaleta C M，Martcheva M.Vaccination strategies and backward bifurcation in an age-since-infection structured model［J］.Mathematical Biosciences，2002，177/178：317-332.

［8］Inaba H，Sekine H.A mathematical model for Chagas disease wtih infection-age-dependent infectivity［J］.Mathematical Biosciences，2004，190（4）：39-69.

［9］Li J，Zhou Y C，Ma Z Z，et al.Epedemiological models for mutating pathogens［J］.Journal on Applied Mathematics，2004，65（1）：1-23.

［10］Zhang Z H，Peng J G.A SIRS epidemic model with infection-age dependence［J］.Journal of Mathematical Analysis and Applications，2007，331（2）：1396-1414.

［11］徐文雄，张仲华.年龄结构SIR流行病传播数学模型渐近分析［J］.西安交通大学学报，2003，37（10）：1086-1089.

［12］Mena-Lorca J，Hethcote H W.Dynamic models of infectious diseases as regulators of population size［J］.Journal of Mathematical Biology，1992，30：693-716.

Global stability of an age-structured SIRS epidemic model

ZHANG Zhong-hua，SUO Yao-hong
（College of Sciences，Xi’an University of Science and Technology，Xi’an 710054，China）

An age-structured SIRS epidemic model with screening strategy and infectionage is formulated.The basic reproductive number is defined.Global stability of equilibria of the model are disucssed by constructing suitable Lyapunov functions.

infection-age；SIRS epidemic model；globally asymptotical stability

O 175

A

1007-2861（2015）03-0336-08

10.3969/j.issn.1007-2861.2014.05.010

2014-09-21

国家自然科学基金资助项目（11201277，10971064，11271125，11402054）；中国博士后基金资助项目（20090461281）；陕西省教育厅专项科研计划基金资助项目（09JK601，12JK0851，2013JK0611）；陕西省自然科学基础研究计划资助项目（2015JM1011）；信阳师范学院种群生态模拟与控制重点实验室开放课题基金资助项目（201004）

张仲华（1977—），男，副教授，博士，研究方向为生物数学.E-mail：wwwzhangzhonghua@163.com