光滑映射芽的平凡性

王美莹，许静波，郭青松

(吉林师范大学 数学学院，吉林 四平 136000)

0 引言

Thom提出的通用开折是突变理论的重要内容，也是奇点理论对数学最重要的贡献之一.通用开折在奇点理论中是一个重要课题，至今已经取得了一些研究成果.文献[1]中讨论了映射芽的通用开折.如果一个函数芽f存在通用开折，那么对f做扰动产生的每一个开折都可由f的通用开折导出，这说明研究通用开折是很有意义的.常用的等价群有左右等价群，接触等价群和右等价群-，在不同等价群作用下可以得到不同通用开折定理.文献[1]对映射芽在各种等价下的通用开折进行了探究，并给出函数芽的有限决定性的概念及结论；在文献[2]中，介绍了在等价和等价子群作用下映射芽的通用开折定理及有限决定性定理.文中定义了右等价群的一个子群，给出了在子群作用下映射芽的等价及开折的概念，讨论了在子群下平凡开折的性质，并给出了光滑映射芽Θ-平凡的必要条件的证明.

1 预备知识与主要结果

记εn为光滑函数在0∈n处的芽组成之集，则εn是一个有单位元的交换环.记n={f∈εn|f(0)=0}为εn的唯一最大理想.设x1,…,xn是n中的坐标函数，则n由x1,…,xn生成[4-7].

定义1.1设U为n中的一个开子集，f:U→p是一个映射，其分量可以用f:(f1,…,fp)来表示.如果每个fi:U→(i=1,…p)都是U上的光滑函数，则称f是U上的光滑映射或C映射.

定义1.2C映射p的一个等价类(其中U为点0的开邻域)是C映射在点0∈n处的芽.等价关系规定如下：p与p是等价的，当且仅当存在点0的一个开邻域W⊂U∩V,使得以为代表的C映射芽记为f:(n,0)→p.

定义1.3设映射芽F:(n×r,0)→(p×r,0)为映射芽f:(n,0)→(p,0)的r-参数开折，由给定，其中u=(u1,…,ur)是开折参数.

定义1.4设映射芽F:(n×r,0)→(p×r,0)是映射芽f:(n,0)→(p,0)的平凡开折，它由F(u,x)=(f(x),u)给定.

定义1.5设F:(p,0)→(q,0)和G:(p,0)→(q,0)是光滑映射芽.如果存在微分同胚ø:(p,0)→(p,0)，使得F=G∘φ,则称F和G是-等价的.

定义1.7设Θ是(p,0)上有限生成的向量场εp-模，且F:(p×,0×0)→(q,0)是光滑映射芽的1-参数族，对充分小t，F(0,t)=0.如果存在向量场δ，将其积分得到微分同胚的1-参数族ø:(p×,0×0)→(p,0)，满足对所有x，有ø(x,0)=x，对充分小t，有ø(0,t)=0，且F(ø(x,t),t)=F(x,0).则称F是Θ-平凡的.

定义1.8设Θ是(p,0)上有限生成的向量场εp-模，且F:(p×,0×0)→(q,0)是光滑映射芽的1-参数族，对充分小t，有F(0,t)=0.如果存在向量场δ∈Θ，将其积分得到微分同胚的1-参数族ø:(p×,0×0)→(p,0)，满足对所有x，有ø(x,0)=x，对充分小t，有ø(0,t)=0，且F(ø(x,t),t)=F(x,0)+ψ(x,t)，其中ψ∈θ(F)，则称F是k-Θ-平凡的.

定理1.1[3]设Θ是(p,0)上有限生成的向量场εp-模，将Θ上的每个向量场进行积分均可得到微分同胚的1-参数族.设F:(p×,0×0)→(q,0)是光滑映射芽，F(0,t)=0.如果pθp)〉.则称族F是Θ-平凡的.

定理1.2设(V,0)⊆(p,0)，且Θ是(p,0)上保持V的所有光滑向量场的模，设F:(p×,0×0)→(q,0)是光滑映射芽，对充分小t，有F(0,t)=0.若族F是Θ-平凡的，则

对t微分，有

那么得到

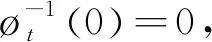
也就是说有一个向量场δ:(p×,0×0)→(p,0)定义为δ(0)=0，使得

通过对δ积分，我们得到一个保持V的微分同胚，即δ∈Θ,

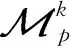
定理1.4[3]设Θ是(p,0)上有限生成的向量场εp-模，将Θ上的每个向量场进行积分均可得到微分同胚的1-参数族.设F:(p×,0×0)→(q,0)是光滑映射芽，对充分小t，F(0,t)=0.如果

定理1.5设(V,0)⊆(p,0)，且Θ是(p,0)上保持V的所有光滑向量场的模.设F:(p×,0×0)→(q,0)是光滑映射芽，对充分小t，F(0,t)=0.若族F是k-Θ-平凡的，则

对t微分，有

那么得到