基于数值模拟的自泵送机械密封正交试验

顾东升，孙见君，马晨波，陆建花



基于数值模拟的自泵送机械密封正交试验

顾东升，孙见君，马晨波，陆建花

（南京林业大学机械电子工程学院，江苏南京 210037）

提出了一种进液槽设置于静环、动压槽分布于动环的自泵送流体动压型机械密封；运用正交试验法设计了自泵送机械密封试验方案，并基于Fluent进行了数值模拟试验，探讨了各试验参数对端面开启力和泄漏率影响的显著性。研究结果表明：在试验参数范围内，影响端面开启力O的显著因素为槽数g、槽长坝长比、槽台宽比和压差；影响泄漏量的显著因素为槽数g、槽长坝长比、槽台宽比、转速和压差；具体表现为开启力随着槽长坝长比、槽台宽比、密封端面内外压差的增大呈上升趋势，随着槽数的增多呈下降趋势；泄漏量随着槽长坝长比、槽台宽比、转速、密封端面内外压差的增大呈上升趋势，随着槽数的增多而呈下降趋势。依据正交试验分析结果，提出了初步优化的密封端面型槽结构。

自泵送机械密封；正交试验；数值模拟；计算流体力学；优化

引 言

近年来，石化、核电等行业的流体机械，如离心压缩机、离心泵，大量采用各种型式的非接触式机械密封用于防止主轴与壳体之间的泄漏[1-3]。Josef[4]提出了一种适用于大轴径、高压涡轮机和压缩机使用的单列螺旋槽流体动静压结合型非接触式机械密封；郝木明等[5]提出了一种在密封环上开设单列特殊型槽，并在型槽中部开设环形沟槽的单列流体动压槽上游泵送机械密封；彭建等[6]提出了一种采用一个动环，而将两个静环对称设置于动环两侧的干气密封。这些密封，通过将阻塞流体“泵入”至型槽根部产生端面开启力[7-8]，进而分离动静环，获得减小端面摩擦磨损的效果，但同时也增大了泄漏量。为了减小泄漏，人们发明了双列流体型槽非接触式机械密封，如Lai[9]的双列螺旋槽端面密封，王玉明等[10]的双环带螺旋槽端面密封，郝木明等[11]的双列流体型槽自润滑非接触式机械密封。这类密封依靠两列螺旋槽在泵送密封流体时泵送方向的不同产生泵汲压差，并利用泵汲压差与密封端面内外侧流体压差相平衡，实现了零泄漏，但它们对密封端面两侧流体压差的严格要求，复杂的结构和较大的安装空间，限制了其应用范围。基于此，孙见君等[12]提出了一种具有流体动压效应的“泵出式”机械密封，有效解决了上述单列和双列螺旋槽机械密封的不足。

目前，国内外针对基于离心泵送原理提出的自泵送机械密封研究并不多见，只有周敏等[13]运用Fluent软件对自泵送型槽进行了三维流场动力学仿真分析，探讨了几何参数和工况参数对自泵送流体动压型机械密封性能的影响。其所研究的自泵送机械密封的动环开设有导流孔，以便向型槽根部输送“泵出”流体，但当动环旋转时，导流孔内的流体由于受离心力的影响，将出现供流不稳现象；其开展的研究并未给出优化的型槽参数。可见，要想让自泵送机械密封应用于工业生产，还有待于进一步研究。

本文拟通过设计正交试验方案，运用Fluent数值模拟计算，探讨几何参数和操作参数对静环设置进液槽的自泵送机械密封性能的影响及其显著性，为进一步优化型槽结构参数或选择操作条件提供基础。

1 静环设置进液槽的自泵送机械密封三维结构及其工作原理

1.1 三维结构

图1为进液槽设置于静环、动压槽分布于动环的自泵送机械密封三维结构图。动环端面由型线为对数螺旋线的螺旋槽区和密封坝组成；静环端面中部设有圆环形进液槽，并在槽内设置6个与密封腔连通的轴向径向组合孔道；流体通过静环上设置的6个轴向径向组合孔道进入静环端面中部的圆环形进液槽中，再进入与之配合的动环的端面螺旋槽内。

1.2 工作原理

静环设置进液槽的自泵送机械密封，其工作原理与离心泵类似。当动环转动时，由于离心力的作用，流入动环螺旋槽中的介质被加速成高速流体，并沿工作面（图2中所示的working face）向动环外径侧流动而被泵送至密封腔内，螺旋槽的根部由于介质的流出形成低压区；与此同时，密封腔内的介质会在压差作用下通过静环上与密封腔连通的轴向径向组合孔道流入进液槽中进入螺旋槽根部，并在离心力作用下重新流入动环螺旋槽内被加速成高速流体而沿工作面被“泵出”至密封腔，形成一次次的自泵送循环；这一次次的自泵送循环过程，一方面，实现了机械密封的自润滑，另一方面，流体在密封面之间的不断循环，把密封面之间的摩擦热及时带走，实现了密封的自冲洗；而离心力的作用，增加了流体流向动环密封面外侧的动力，降低了流体流向动环密封面内侧的泄漏率；特别是，离心力的作用，使得进入螺旋槽中的含有固体颗粒的被密封流体，能够产生固体颗粒与基质分离，其中密度大的固体颗粒获得较大的离心力，随流体被泵出重新送至密封腔中，不进入密封坝区，避免了密封面之间的磨粒磨损。被螺旋型槽加速成高速的流体，在被泵出流体型槽的过程中，随着流体型槽的流通截面积的逐渐增大，流速降低，压力增大，形成分离动环和静环的开启力。此外，静环上的进液槽还具有收集自润滑、自冲洗介质和防止泵送介质不均匀以及流体型槽进口处的流体补充不及时出现空化的作用。

考虑到自泵送机械密封是基于离心泵送原理提出的，因此借鉴离心泵扬程和流量公式可推导出自泵送流体动压型机械密封的能量头与槽内介质流量之间的关系及泄漏率L与密封面两侧压差Δ之间的关系[13]

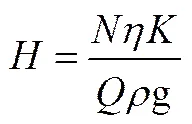
(2)

式中，为与流体槽数相关的环流系数，恒小于1，当槽数无限多时趋近于1；=mhv为泵送效率，反映能量损失的程度（m为机械效率，h为水力效率，v为容积效率）；为轴功率；为流体流量；为密封介质密度；L为泄漏率；为槽台宽比；为密封介质动力黏度；o为端面流体膜厚；Δ为密封端面两侧的压差；g为密封坝两侧的压差；o为流体膜外半径；为密封面宽度；为密封坝宽度。

2 正交试验方案设计

研究对象为进液槽设置于静环、动压槽分布于动环的新型自泵送机械密封，欲寻找显著影响自泵送机械密封性能的因素。

表征自泵送机械密封的结构参数有螺旋角、槽数g、螺旋槽深g、环槽深、环槽宽、槽长坝长比、槽台宽比，密封端面的内、外半径i和o，此外，自泵送机械密封性能与操作参数（压差、转速）和密封端面间流体膜厚o也有很大关系。为了便于分析和比较，试验中选用常温水作为密封介质，取黏度=1.003´10-3Pa·s，密封端面外半径o=89 mm，内半径i=53 mm；同时为了保证密封端面间有适当的液膜刚度、开启力、较小的泄漏量，参考密封标准中对密封端面粗糙度的要求，取膜厚o=1.2mm。因此总的变化因素为9个，各因素的水平数设为8，各水平对应的值见表1，根据因素水平表选用正交表L64(89)，设计正交试验方案见表2。目标参数为密封端面开启力和泄漏量。假设各影响因素均为独立作用条件，无交互作用。

表1 各水平对应的数值
Table 1 Corresponding values of,g,g,,,,,,with different levels

表2 数值模拟结果
Table 2 Results of numerical simulation

Table 2 (continued)

3 数值模拟计算

3.1 基本假设

流体膜润滑机械密封的流场计算十分复杂。为简化计算，对流体膜做如下几种假设[13]：

（1）密封端面间的流体温度、黏度不随时间变化，且其为连续介质流动；

（2）密封端面间的流体作层流流动，满足牛顿内摩擦定律；

（3）液膜厚度薄，忽略流体压力与密度在其厚度方向上的变化；

（4）密封环温度、密封材料性质不随时间变化；

（5）流体介质与密封表面之间无相对滑移；

（6）密封端面光滑，忽略其粗糙度的影响；

（7）进液槽的进口孔道只起导流作用，对微间隙流体计算模型无影响。

3.2 采样计算区域几何模型

被研究的对象系三维轴对称流场，取其中任一螺旋槽区域为计算区域[14]，如图2所示。

3.3 控制方程

根据基本假设和采样计算模型，可知密封端面间的流体作稳态流动，故满足Reynolds方程[15-16]

对上述方程做量纲1化处理，得

(4)

式中，i，i，i，i(ic)，=；i为密封端面内半径，i为内径侧压力，为槽深，为非槽区液体膜厚，为端面平均线速度，为量纲1压缩数。

3.4 求解器及边界条件的设置

由于式(3)、式(4)为非线性偏微分方程，无法用解析法直接求解，故本文计算使用商用软件Fluent 6.3进行；选择3D三维单精度求解器，求解器模型设置为Laminar层流模型，压力速度耦合采用SIMPLEC方法，扩散项的离散格式采用中心差分格式，对流项的离散格式采用二阶迎风格式，模型收敛绝对精度设为10-8[17]；采用Reynolds边界条件[18-19]设置强制性边界条件和周期性边界条件。

（1）强制性边界条件

在内径出口CD面上，有i（大气压）。

在外径出口AB面上，有o（介质压力）。

在环槽进口EFGH面上，有o（介质压力）。

（2）周期性边界条件

在边界AD和BC面的压力相等：|AD=|BC，即(+2p/g)=()。

在边界EH和FG面的压力相等：|EH=|FG，即(+2p/g)=()。

根据质量流量守恒，流过边界AD+EH和BC+FG面的质量流量相等：|AD+|EH=|BC+|FG；流过AB+DC面的流体质量等于流过环槽入口EFGH的流体质量：|EFGH=|CD +|AB。

3.5 网格划分

由于螺旋线曲率较大，容易导致螺旋槽尖端处网格产生畸变，加之，流体膜厚方向与径向的尺寸相差也很大，如果直接使用Gambit软件对计算区域进行自动网格划分，很难满足计算精度要求，故本文在研究中采用线-面-体网格划分顺序手动划分网格。其中，对边线的划分方式采用Interval count划分，对面采用Tri选项下的pave方式划分，再利用Cooper方法生成流体膜和型槽部分的网格。考虑到网格数太少会使计算结果产生过大的误差，而网格数过多又会使得计算量变大，耗时长，且当网格数增加到一定数量时对结果的精度影响很小等因素，通过不断改进网格划分数量，权衡划分的网格质量及计算机运算能力，最终将膜厚方向划分为6层网格，螺旋槽槽深方向划分为8层网格，进液槽槽深方向划分为8层，生成总数为683216的网格，划分好的网格如图3所示。

3.6 数值模拟正交试验结果及分析

3.6.1 试验结果

按照前面介绍的试验方案和计算方法，进行数值模拟，得到各试验号的计算结果，如表2所示。

3.6.2 结果分析

根据正交试验分析理论进行综合直观分析，将每一因素各水平下的目标值求和并取均值，据此作出目标值与影响因素间的关系图[20]。各因素与开启力O、泄漏量的关系分别见图4和图5，具体说明如下。

（1）O随、g、g、、、、、、的变化关系

由图4可知，对端面开启力O有显著影响的因素是槽数g、槽长坝长比、槽台宽比和密封端面内外压差。这是由于g对应式(1)中的，对应式(2)中的与，对应式(2)中的，对应式(2)中的D，所以当g变化时，式(1)与式(2)中的、、、、D也会随着直接发生改变，因此这些因素对O影响显著。此外，从图4还可以发现O随g增大呈下降趋势，随、、的增大呈迅速上升趋势；环槽宽的影响不大；螺旋角、螺旋槽深g、环槽深和转速对O没有显著影响。因此要获得较大开启力，自泵送机械密封应取较少的槽数，较大的槽长坝长比和槽台宽比，并在较高的压差下工作。

（2）随、g、g、、、、、、的变化关系

由图5可知，对泄漏量有显著影响的因素是槽数g、槽长坝长比、槽台宽比、转速和密封端面内外压差。跟前文类似，g对应式(1)中的，对应式(2)中的与，对应式(2)中的，对应式(1)中的，对应式(2)中的D，所以当g变化时，式(1)与式(2)中的、、、、、D也会随着直接发生改变，因此这些因素对影响显著。此外，从图5中还可以发现，随g的增大呈下降趋势，随、、、的增大呈迅速上升趋势；环槽宽的影响不大；螺旋角、螺旋槽深g、环槽深对没有显著影响。因此要获得较小的泄漏量，自泵送机械密封应取较多的槽数、较小的槽长坝长比和槽台宽比，并在较低的转速和压差下工作。

4 验证试验

正交试验方案的一个突出优点是可以根据理论分析确定试验参数范围内的较优值。由前面的分析可知，本次试验中对密封性能有显著影响的因素是g和，影响不显著的因素为g。具体表现为：O随着的增大呈上升趋势，随着g的增多呈下降趋势；随着的增大呈上升趋势，随g的增多而呈下降趋势。根据这一分析结论，并通过综合平衡原则[21]，设计一新的动、静环密封结构，取结构参数为g=16、=22°、g=50mm、=500mm、=2 mm、=0.5、=0.4，操作参数=4000r·min-1、=1.8 MPa。为了确定其是否为较优方案，按照前面叙述的计算方法进行了数值模拟验证计算，结果得：O=1.62000352 kN，=1.318896281 ml·h-1。通过比较可以发现，在相同的压差或者转速下，此结构自泵送机械密封的性能明显优于正交表中的试验方案。可见，在自泵送机械密封的结构优化中运用正交试验方案仅用较少的试验次数就能得到较优的密封结构参数，体现了正交试验的优点，同时也为自泵送机械密封结构的进一步优化与研究提供了技术支撑。

5 结 论

（1）提出了一种进液槽设置于静环、动压槽分布于动环的泵出型机械密封结构。这种结构的自泵送流体动压型机械密封与以往流体泵入型的结构型式不同，无须其他阻塞流体供应辅助系统；

（2）应用正交试验分析方法分析了自泵送机械密封性能的影响因素及显著性，提出了初步优化的密封结构及其对应的操作参数；

（3）在试验参数的取值范围内，对端面开启力O有显著影响的因素是槽数g、槽长坝长比、槽台宽比和压差，具体表现为开启力随着槽长坝长比、槽台宽比、密封端面内外压差的增大呈上升趋势，随着槽数的增多呈下降趋势；对泄漏量有显著影响的因素是槽数g、槽长坝长比、槽台宽比、转速和压差，具体表现为泄漏量随着槽长坝长比、槽台宽比、转速、密封端面内外压差的增大呈上升趋势，随着槽数的增多而呈下降趋势。此外，环槽宽对自泵送机械密封性能的影响不大，螺旋角、螺旋槽深g、环槽深对自泵送机械密封性能没有显著影响。

符 号 说 明

References

[1] Etsion I.A new concept of zero-leakage non-contacting face seal [J]., 1984, 106(3): 338-343.

[2] Fischbach M J. Dry seal applications in centrifugal compressors [J]., 1989, 68(10): 47-51.

[3] Lai T. Development of non-contacting, non-leaking spiral groove liquid face seals [J]., 1994, 50 (8): 625-631.

[4] Josef Sedy.Self aligning spiral groove face seal[P]: US, 4212475 A. 1980-7-15.

[5] Hao Muming(郝木明), Hu Danmei(胡丹梅), Ge Jingpeng(葛京鹏), Yang Huixia(杨惠霞).Linear fluid dynamic channel upstream pumping machine seal[P]: CN, 2432391Y. 2001-5-31.

[6] Peng Jian(彭建), Hong Xianzhi(洪先志), Wang Anjing(王安静), Meng Xiugui(孟秀贵).Dry gas seal of centrifugal machine[P]: CN, 201644244U. 2010-11-24.

[7] Wang B, Zhang H, Cao H. Flow dynamics of a spiral-groove dry-gas seal [J]., 2013, 26(1): 78-84.

[8] Buck G S, Volden D. Upstream pumping: a new concept in mechanical sealing technology [J]., 1990, 46(4): 213-217.

[9] Lai Weitang. Face seal with double spiral grooves[P]: US, 5201531A. 1993-4-13.

[10] Wang Yuming(王玉明), Li Keyong(李克永).End face seal of double loop with spiral groove[P]: CN, 1067753C. 2001-6-27.

[11] Hao Muming(郝木明), Hu Danmei(胡丹梅), Ge Jingpeng(葛京鹏), Yang Huixia(杨惠霞).Self-lubricating non-contact mechanical seal with double rows of fluid dynamic pressure groove[P]: CN, 2442034Y. 2001-8-8.

[12] Sun Jianjun(孙见君), Wang Min(王敏), Zhou Min(周敏), Tu Qiao’an(涂桥安). Self-pumping mechanical seal based on fluid dynamic pressure principle [P]: CN, 103267132A.2013-8-28.

[13] Zhou Min(周敏), Sun Jianjun(孙见君), Ma Chenbo(马晨波), Yu Qiuping(於秋萍). Performance analysis of hydrodynamic mechanical seals based on self-pumping principle [J].(化工学报), 2015, 66(2): 687-69.

[14] Wang Q, Chen H L, Liu T,. Research on performance of upstream pumping mechanical seal with different deep spiral groove//IOP Conference Series: Earth and Environmental Science[C].IOP Publishing, 2012, 15(7): 072019-072027..

[15] Basu P. Analysis of a radial groove gas face seal [J]., 1992, 35(1): 11-20.

[16] Nicolescu B N, Petrescu T C.Homogenization of the Reynolds equation in the radial face seals Case [J]., 2013, 81(1): 35-52.

[17] Xu Jing(徐静).Technology of spiral groove dry gas seals for pump[D]. Nanjing: Nanjing Forestry University, 2012.

[18] Ruan B. Finite element analysis of the spiral groove gas face seal at the slow speed and the low pressure conditions-slip flow consideration [J]., 2000, 43 (3): 411-418.

[19] Hu X P, Song P Y. Theoretic analysis of the effect of real gas on the performance of the T-groove and radial groove dry gas seal [J]., 2013, 271: 1218-1223.

[20] Huang Weijun(黄维军), Deng Xianhe(邓先和), Huang Debin(黄德斌). Shape optimization of transversely-ridged tube by orthogonal numerical simulation test [J].()(化工学报), 2005, 56(8): 1445-1449.

[21] Li Yunyan(李云雁), Hu Chuanrong(胡传荣).Experiment Design and Data Processing(试验设计与数据处理)[M].Beijing: Chemical Industry Press, 2008: 132-134.

Orthogonal test of self-pumping mechanical seals based on numerical simulation

GU Dongsheng, SUN Jianjun, MA Chenbo, LU Jianhua

(College of Mechanical and Electrical Engineering, Nanjing Forestry University, Nanjing 210037, Jiangsu, China)

A kind of self-pumping hydrodynamic mechanical seal, that the liquid inlet groove was arranged on the stationary ring and the dynamic pressure groove was distributed on the rotating ring, was put forward based on the principle of centrifugal pump. The experimental scheme of the self-pumping mechanical seals was designed by orthogonal test. The numerical simulation experiments were carried out based on Fluent, including discussing the significant effects of every parameter on the face opening force and the leakage rate. The numerical results showed that the groove numberg, the ratio of groove length and dam length, the ratio of groove width and ridge width, and the pressurewerethe significant factors affecting the opening forceOand the leakage ratewithin the experimental ranges. Besides, the rotate speedalso affectedsignificantly. Specifically,Owas increased with increasing,andwhile decreased with increasingg. The influence of,,andgonwassimilar to that onO. Butwas also increased with increasing. The preliminary optimization of sealing structure was brought forward by analyzing the results of orthogonal test.

self-pumping mechanical seal; orthogonal test; numerical simulation; CFD; optimization

10.11949/j.issn.0438-1157.20150204

TH 136

国家级大学生实践创新训练计划资助项目（201410298051Z）。

2015-02-09.

Prof. SUN Jianjun, sunjj65@163.com

supported by the National Practice Innovation Training Program Funded Projects for the College Students (201410298051Z).

A

0438—1157（2015）07—2464—10

2015-02-09收到初稿，2015-03-16收到修改稿。

联系人：孙见君。第一作者：顾东升（1990—），男，硕士研究生。