竖直窄矩形通道内环状流的流动传热特性

陈冲，高璞珍，谭思超，余志庭，陈先兵



竖直窄矩形通道内环状流的流动传热特性

陈冲，高璞珍，谭思超，余志庭，陈先兵

（哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨 150001）

为了研究竖直窄矩形通道内环状流的流动传热特性，建立了窄矩形通道内环状流的数学物理模型，并进行了实验验证。通过数值求解环状流的数学物理模型得到了环状流区域的压降梯度、沸腾传热系数和液膜内的速度分布。结果表明窄矩形通道内的环状流模型能够很好地预测环状流区域的压降梯度和沸腾传热系数，而且环状流液膜内速度在法向的分布是非线性的，在层流边界层区速度梯度较大。热通量和窄矩形通道的尺寸对液膜的流速有很大影响，随热通量的增加和窄矩形通道尺寸的减小液膜的流速逐渐增加，然而质量流速对液膜流速的影响较小，而且随质量流速的增加液膜的速度逐渐减小。

窄矩形通道；液膜流速；环状流；相平衡；传热；相变

引 言

窄矩形通道具有结构紧凑和传热效率高等独特的热工水力特性，使其成为高性能紧凑式换热器的主要结构形式之一，目前广泛应用在核能、化工、电子冷却、高能激光等行业中。窄矩形通道能够消除或减轻两相流的不稳定性，其流动沸腾传热系数比一般的光管提高60%～90%[1]。Wang等[2]对矩形微槽内水的流动沸腾换热进行了可视化研究，结果表明在低壁面过热度的工况下窄矩形通道内的主要流型为环状流。Sun等[3]、Su等[4]、Du等[5]在窄通道两相沸腾实验中得出了相似的结论，并认为窄通道中的主要流型为环状流。Joseph等[6]对环状流在通道内的稳定性进行了实验研究，结果表明当液膜工质黏度较大、气芯工质黏度较小时环状流能够保持稳定的发展，同时从机理上解释了液膜初始的波动状态和环状流形成的原因。Okawa等[7]、Han等[8]、Sawant等[9]、Barbosa等[10]、Cioncolini等[11]通过不同的实验方法和机理分析给出了不同工况范围内气芯液滴夹带率和沉积率的经验关系式。李卫东等[12]在考虑液滴沉积和夹带机理的基础上建立了水平管道环状流周向液膜厚度分布的理论模型，该模型能够很好地预测水平管道环状流区域的液膜厚度。Qu等[13]认为在窄通道中环状流起始点的质量含气率与Martinelli参数有关，并给出了窄通道环状流起始点质量含气率的经验关系式。Fu 等[14]根据流体的质量、动量和能量方程建立了圆管的环状流模型，得到了环状流区域的沸腾传热系数和压降梯度，模型的理论计算值和实验值的误差在±25%之内。Su等[4]建立了窄环隙管的环状流模型，该模型能够很好地预测窄环隙通道环状流区域的压降梯度和沸腾传热系数，并给出了液膜厚度的变化趋势。Du等[5]利用环状流模型对窄矩形通道的临界热通量（CHF）进行了预测，结果表明窄矩形通道的临界热通量随系统压强的增加而逐渐增加，并且在2～4 MPa区间存在一个峰值，在相同的实验工况下临界热通量随质量流量和入口过冷度的增加而增加，随窄矩形通道高度的增加而增加，而且窄矩形通道的宽度对临界热通量影响不大。

综上所述，关于圆管环状流模型的文献较多，同时环状流模型能够较好地预测压降梯度和沸腾传热系数。目前窄矩形通道的研究主要集中在单相流体的流动传热特性方面以及通道内流场和温度场的数值模拟，关于沸腾工况下窄矩形通道内的流动传热特性的研究较少，这是由于窄矩形通道的尺寸很小，在低含气率下就有可能出现很大的空泡份额，而且沸腾工况下通道内的主要流型为环状流。本研究根据液膜的质量、动量和能量方程以及气芯的动量方程建立了窄矩形通道的环状流模型，并通过实验进行验证，分析了窄矩形通道环状流区域的流动传热特性。

1 窄矩形通道内环状流模型

1.1 环状流模型的基本假设

窄矩形通道内环状流的数学物理模型示于图1。通道内的流型主要为单相流、泡状流、搅混流和环状流。在环状流区域，液膜和夹带液滴的气芯之间存在着质量、动量和能量交换，即液膜不断地蒸发进入气芯，气芯也会卷吸液膜，同时快速运动的液滴还会与液膜接触而沉积在气液交界面处。当液滴的沉积、夹带和液膜蒸发之间达到平衡时，在通道的法向方向液膜的厚度将会到达一个稳定值，整个环状流区域处于稳定的流动状态。在分析窄矩形通道内环状流区域的流动和传热特性时对模型进行一些假设：①在通道环状流区域流型始终维持规则的环状流；②流体是不可压缩的；③液膜厚度周向分布均匀且压力法向分布均匀；④液膜为稳态流动，忽略轴向的导热和对流换热，只有沿径向的导热；⑤液滴在气芯中的分布是均匀的，而且液滴与单相气之间没有滑移。

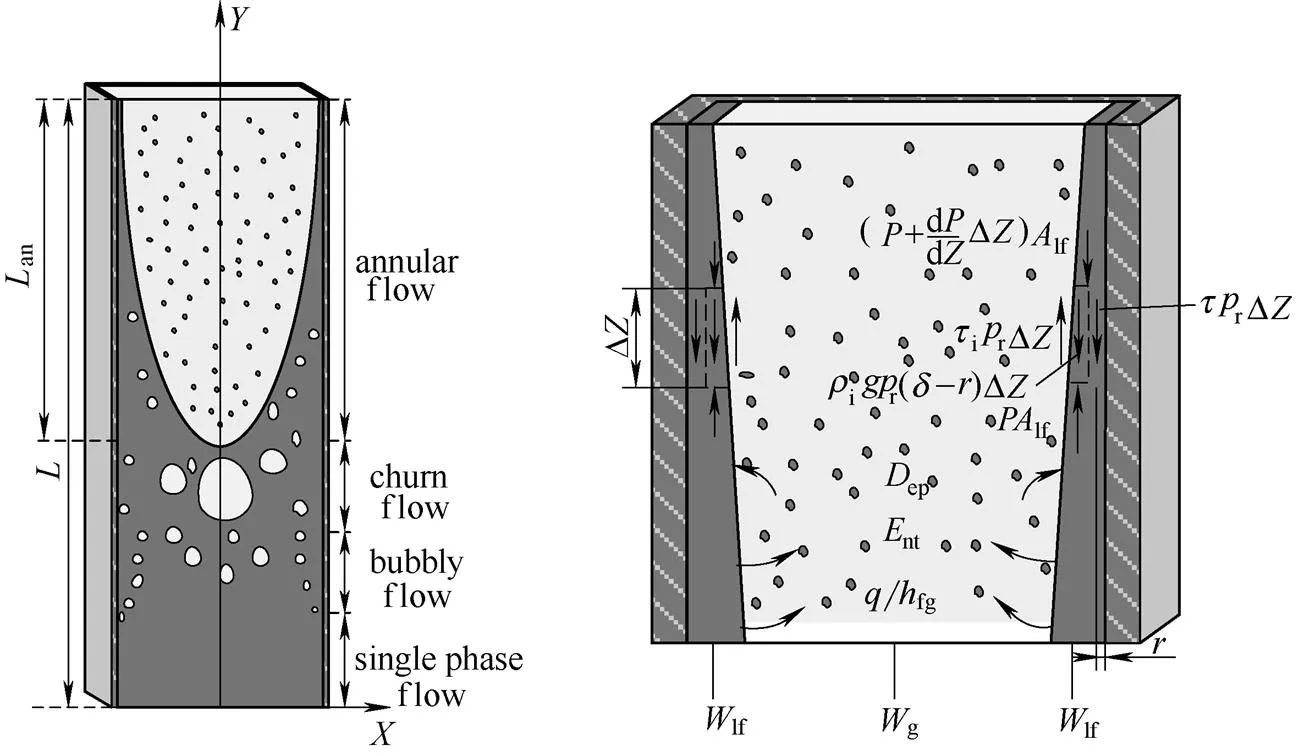
图1 窄矩形通道环状流模型

1.2 环状流起始点

窄矩形通道加热实验段的材料为不锈钢，实验段外围有保温装置，不能实际观察到环状流起始点的位置。由热平衡方程得

环状流起始点处的质量含气率an是一个重要的参数。Taitel等[15]在预测气液两相流流态转换的研究中提出用Martinelli参数预测环状流起始点处的质量含气率，并认为当an1.6时通道开始出现环状流。

在实验数据处理时选择质量含气率大于an的区域，这样就能确保实验流体处于环状流区域。

1.3 液膜区的控制方程

气芯和液膜之间的质量交换会导致液膜的质量流量随实验段轴向距离的变化而变化，液膜的质量守恒方程[16]为

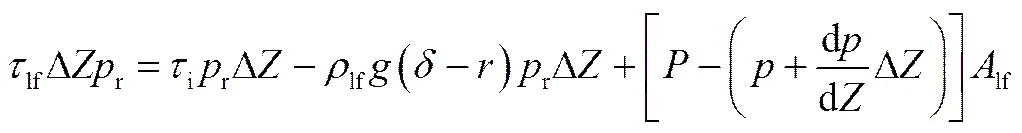
根据环状流模型的假设，液膜的能量方程为

边界条件

环状流区域，两相沸腾传热系数

根据牛顿内摩擦定律，液膜内部的剪切力

边界条件

涡流黏度用来描述液膜内部的紊流程度，由Fu-Klausner关系式[14]得

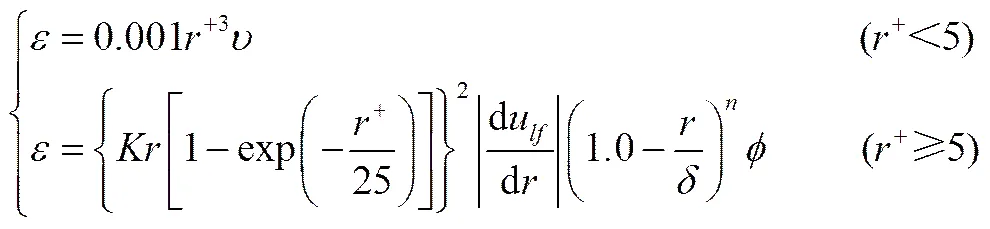
液膜的质量流量

1.4 气芯区的控制方程

根据环状流模型的基本假设，环状流区域的压力在法向的分布是均匀的，环状流区域的压力梯度dd可以由气芯的动量方程计算得到。

1.5 气液界面区方程

气液交界面处的剪切力是气芯和液膜出现速度差时产生的相互作用力，同时气液交界面的剪切力是计算液膜质量流量和流速的重要参数。由Fore关系式[17]

环状流区域，气芯液滴的沉积率是指单位时间内气芯液滴沉积在单位面积液膜上的质量。对于均匀加热的窄矩形通道，液滴沉积率由两部分组成：一个是液滴与液膜接触产生的正效应沉积率ep,p，另一个是气液交界面处的蒸发阻碍液滴与液膜接触而产生的负效应沉积率ep,b。

矩形通道环状流气芯液滴的沉积率为

Kataoka等[18]根据绝热充分发展的环状流模型得出正效应沉积率为

Milashenko等[19]给出了液滴的负效应沉积率

窄矩形通道环状流气芯液滴的夹带率由两部分组成：一个是气芯对液膜产生扰动作用，使液膜产生波动继而将液膜卷吸入气芯，称为液膜波动夹带率nt,w；另一个是在不断加热的通道内面产生气泡，气泡在气液交界面处破裂产生液滴，称为沸腾夹带率nt,b。气芯液滴夹带率为

Okawa等[7]认为气液交界面处的切应力与水的表面张力的比值在预测液膜波动夹带率时起主要作用，并给出了液膜波动夹带率的关系式

Ueda等[20]给出了沸腾夹带率的关系式

用数值解法求解上述方程组，可以得到窄矩形通道环状流区域的沸腾传热系数、压降梯度、液膜流速等流动传热特性参数。

2 窄矩形通道热工水力实验装置

关于周边加热的窄矩形通道环状流的文献和数据点很少。为了验证窄矩形通道的环状流模型，设计了窄矩形通道热工水力实验装置。

窄矩形通道热工水力实验装置示于图2。整个实验装置由实验回路和冷却回路组成。冷却回路由室外冷却塔、水箱、循环水泵和冷凝器组成，它的主要作用是冷却实验回路中的热流体。实验回路由窄矩形实验段、冷凝器、主泵、稳压器、电磁流量计、预热器和直流电源组成。直流电源用来给窄矩形实验段加热，其最大加热功率为100 kW；预热 器用来维持实验段入口温度，其最大加热功率为45 kW；稳压器与高压氮气瓶通过软管道连接，用来维持系统压力。实验启动时，主泵为整个实验回路提供循环动力，实验工质首先在预热器中加热，达到预定温度后进入窄矩形实验通道，在实验通道中由直流电源继续加热，直到出口含气率达到预定的要求，当实验工况稳定后采集实验通道的壁面温度、压差和系统压强，之后流体流入冷凝器，被冷却回路冷却，最后经过主泵流入预热器，进入下一个循环。

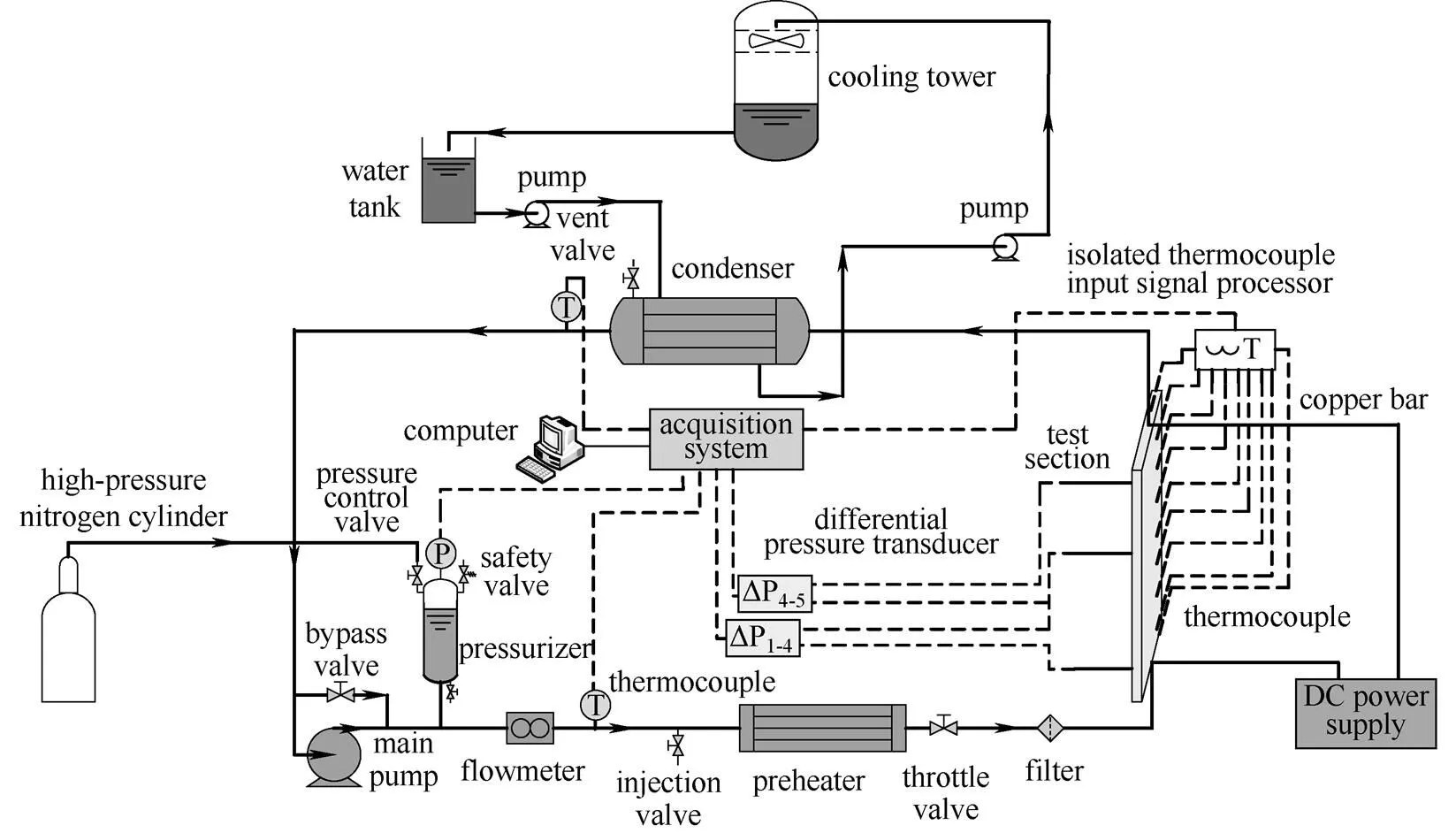
图2 实验装置

窄矩形通道的尺寸为2 mm×40 mm，热电偶距离入口处的距离为/e32、72、125、180、217、253、274，引压孔的编号从入口到出口分别为1、4、5，距离入口的距离为/h56、230、282，可以测量1-4段和4-5段压差。使用电磁体积流量计测量工质的流量，量程为0～3 m3·h-1，测量准确度为±0.3%；压降测量使用的是压力传感器，其量程为200 kPa，测量准确度为±0.2%；7组热电偶的测量误差在±0.3℃以内。

3 模型验证及结果分析

3.1 窄矩形通道环状流模型验证

轴向压降梯度和两相沸腾传热系数的实验值与窄矩形通道环状流模型的计算值的对比示于图3和图4。

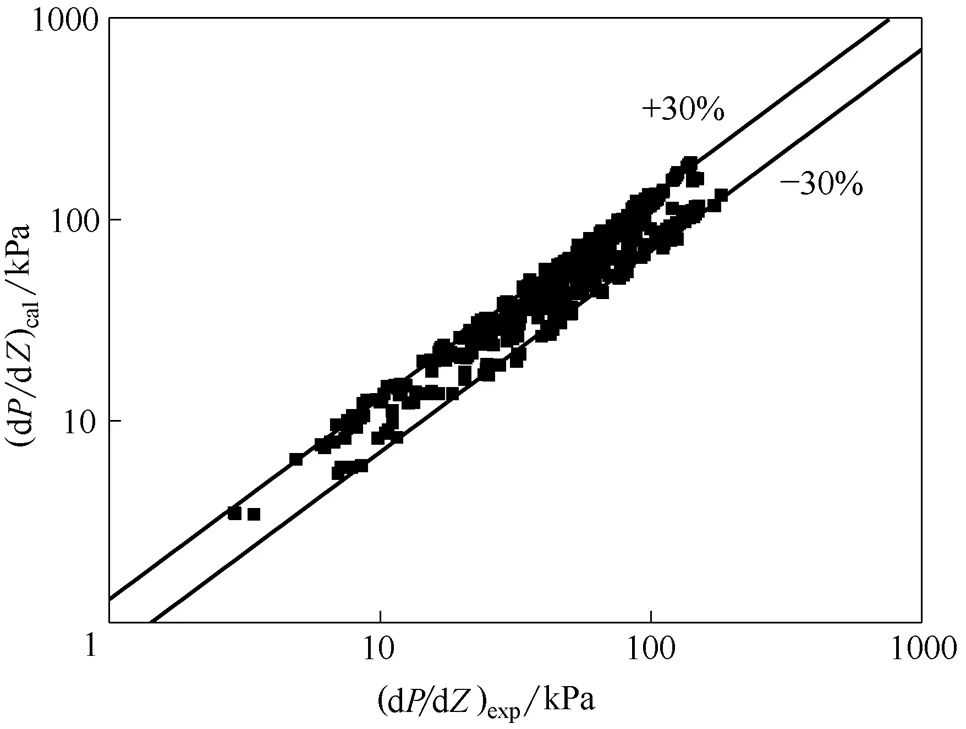
图3 压降梯度实验值与计算值的对比

图4 传热系数实验值与计算值的对比

图3给出的窄矩形通道轴向压降梯度的误差在±30%以内，数据的平均绝对误差（MEA）为20%。在±30%的放射线内窄矩形通道环状流轴向压降梯度计算值大于实验值的数据点的份额为62.3%，而且这些数据点大部分集中在小于75 kPa的范围内。这主要是因为在实验过程中为了确保测量实验段压差的压差变送器的量程能够满足高质量含气率的实验工况而选取了量程为200 kPa的压差变送器。在小功率或者质量含气率较小时，此压差变送器采集的灵敏度不够，也就是说，当功率或者质量含气率的微小变化引起压差变化时，并没有被压差变送器采集，或者采集的数值比真实值要小，所以会导致实验测量的结果比计算的结果小，尤其在压差小于75 kPa的范围。

窄矩形通道沸腾传热系数的实验值和模型计算值的对比示于图4，其误差在±30%以内，数据的平均绝对误差（MEA）为19.6%。

综合上面的分析以及图3和图4显示的数据分布，可以说明用环状流模型预测窄矩形通道轴向压降梯度和沸腾传热系数是可靠的。

3.2 环状流液膜内部的流速分布

在通道尺寸和质量流速不变的工况下热通量对环状流液膜内流速分布的影响示于图5 (a)，横坐标是距离壁面的量纲1距离，。图5 (a)表明，随着热通量的增加，液膜内流速逐渐增加。这主要是因为随着热通量的增加液膜的厚度减小，同时环状流气芯内蒸汽量增加，蒸汽的速度加大，进而使气液交界面处液膜的流速增加，从而带动内部流体流速的加大。由图5 (a)还可以看出，在定热通量情况下液膜内部流速的分布并不是线性的关系，液膜内流体速度的梯度是随量纲1距离的增加先保持不变，然后减小，最后非线性地增加，尤其在靠近气液交界面处流体的速度梯度增加得很快。这主要是因为在靠近加热壁面处存在黏性底层，黏性底层内部是层流流动，在黏性底层区域液膜流速随量纲1距离的增加是线性增加的，黏性底层的厚度在25 μm左右，由于黏性底层靠近壁面且厚度很小，其内部的速度梯度相对较大。在黏性底层上面是紊流区域，液体质点在紊流区域的不规则运动会使流体的速度趋于均匀化，速度梯度相对较小，即液膜的速度随量纲1距离的增加变化不是很剧烈。在靠近气液交界面处流体的速度梯度很大，主要是因为气液交界面处的流体受到环状流气芯的剪切应力作用，使流体加速，但这种加速的影响效果由于紊流质点的不规则运动只能维持在很短的距离之内。所以液膜内流速的法向分布并不是线性的，在不同的区域有不同的速度梯度。

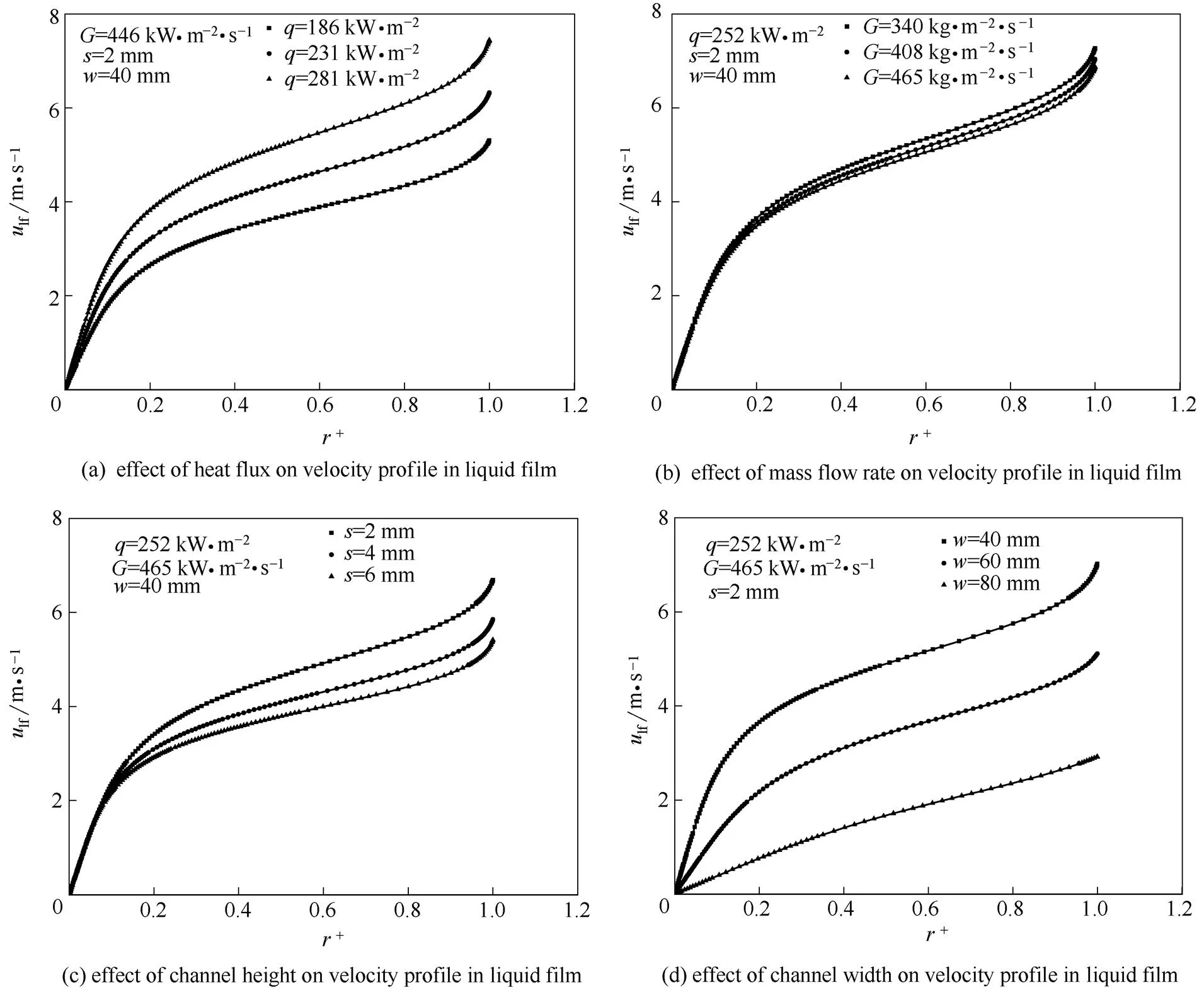
图5 液膜内的速度分布

不同的质量流速对液膜流速分布的影响示于图5 (b)。随着质量流速的增加，液膜的速度减小，但是液膜速度减小的幅度很小，即质量流速对液膜速度的影响效果较小。产生这种影响的主要因素在于随着质量流量的增加液膜的厚度逐渐增加，同时随着质量流量的增加气液交界面处液体的蒸发量减小，环状气芯内蒸汽量减小，导致整个环状气芯的速度减小，气芯和气液交界面处液膜的速度差减小，气芯对液膜的加速作用减小，液膜的速度减小。

不同矩形通道高度对环状流液膜流速分布的影响示于图5 (c)。随着通道高度的增加，液膜流速逐渐减小，主要是因为随着矩形通道高度的增加环状流液膜的厚度逐渐增加，同时随着通道高度的增加在环状流区域气芯的截面积增加，在相同的蒸汽蒸发量的工况下气芯的流速会降低，气芯对液膜的剪切力减小，在两者的共同作用下液膜内的流速会逐渐降低。

不同矩形通道宽度对液膜流速分布的影响示于图5 (d)。随着矩形通道尺寸的增加，液膜的流速减小，主要是因为随着通道宽度的增加液膜的厚度减小，而且环状流气芯的截面增加，气芯的流速减小，气芯对液膜的作用力减小，所以随着通道宽度的增加液膜的流速减小，而且速度减小的幅度较大。在图5 (d)中还可以看出，随着通道宽度的增加，液膜流速的分布逐渐趋于线性分布，这主要是因为随着通道宽度的增加液膜的厚度加速地减小，在通道宽度80 mm时液膜的厚度为36.5 μm，基本处在层流边界层区域，同时气芯和液膜的速度差较小，气芯对液膜的作用力较小，则液膜速度随量纲1距离的增加基本呈线性关系。

4 结 论

（1）根据质量、动量和能量方程建立的窄矩形通道环状流模型能够很好地预测两相压降梯度和沸腾传热系数，模型计算值和实验值的误差在±30%以内，平均绝对误差分别为20%和19.6%。

（2）在环状流区域液膜速度沿法向的分布是非线性的，在层流边界层区域速度梯度较大，在紊流边界层区域速度梯度较小，在靠近气液交界面处速度梯度非线性地增加。

（3）环状流液膜的速度随热通量的增加和通道尺寸的减小而逐渐增加，随质量流速的增加而减小，而且热通量和通道尺寸对液膜流速的影响效果较大。

符 号 说 明

A——通道截面面积，m2 De——当量直径，m Dep——液滴沉积率，kg·m2·s-1 Ent——液滴夹带率，kg·m2·s-1 g——重力加速度，m·s-2 hfg——汽化潜热，kJ·kg-1 htp——沸腾传热系数，kW·m-2·℃-1 L——加热段长度，m P——压强，MPa pr——湿周，m q——热通量，kW·m-2 r——距离壁面长度，m s——矩形通道高度，m T——温度，℃ u——速度，m·s-1 W——质量流量，kg·m-2·s-1 w——矩形通道宽度，m X——Martinelli参数 x——质量含气率 α——空泡份额 δ——液膜厚度，m η——热扩散率，m2·s-1 μ——动力黏度，kg·m-1·s-1 ρ——密度，kg·m-3 σ——表面张力，N·m-1 τ——剪切应力，N·m-2 φ——液滴夹带份额 下角标 an——环状流区域 c——环状流气芯 cal——计算值 exp——实验值 g——气相 i——气液交界面 in——实验段入口 l——液相 lf——液膜 sat——饱和态 w——壁面

References

[1] Pu Pengfei (蒲鹏飞), Pan Liangming (潘良明), Li Wushen (李午申), Huang Yongjun (黄永军). Annular flow analysis model for boiling heat transfer in vertical narrow rectangular gap [J].(热科学与技术), 2005, 4 (3): 208-212

[2] Wang Jihui, Tang Dawei, Yan Xiaohong. An experimental study on the flow boiling heat transfer and its visualization of water in a rectangular micro-groove horizontally [J]., 2007, 24 (1): 34-38

[3] Sun Shufeng, Wu Yuyuan, Zhao Rongyi. The numerical calculation of heat transfer performance for annular flow of liquid nitrogen in a vertical annular channel [J]., 2001, 41 (2001): 231-237

[4] Su Guanghui, Gou Junli, Qiu Suizheng, Yang Xiaoqiang, Jia Dounan. Theoretical calculation of annular upward flow in a narrow annuli with bilateral heating [J]., 2003, 225 (2003): 219-247

[5] Du D X, Tian W X, Su G H, Qiu S Z, Huang Y P, Yan X. Theoretical study on the characteristics of critical heat flux in vertical narrow rectangular channels [J]., 2012, 36 (2012): 21-31

[6] Joseph D D, Bannwart A C, Liu Y J. Stability of annular flow and slugging [J]., 1996, 22 (6): 1247-1254

[7] Okawa Tomio, Kataoka Isao. Correlations for the mass transfer rate of droplets in vertical upward annular flow [J]., 2005, 48 (23/24): 4766-4778

[8] Han Huawei, Gabriel Kamiel S, Wang Zhaolin. A new method of entrainment fraction measurement in annular gas-liquid flow in a small diameter vertical tube [J]., 2007, 18 (2): 79-86

[9] Sawant Pravin, Ishii Mamoru, Mori Michitsugu. Droplet entrainment correlation in vertical upward co-current annular two-phase flow [J]., 2008, 238 (6): 1342-1352

[10] Barbosa Jr J R, Hewitt G F, Konig G, Richardson S M. Liquid entrainment, droplet concentration and pressure gradient at the onset of annular flow in a vertical pipe [J]., 2002, 28 (6): 943-961

[11] Cioncolini Andrea, Thome John R. Entrained liquid fraction prediction in adiabatic and evaporating annular two-phase flow [J]., 2012, 243 (2012): 200-213

[12] Li Weidong (李卫东), Li Rongxian (李荣先), Wang Yueshe (王跃社), Zhou Fangde (周芳德). Model for prediction of circumferential distribution of film thickness in horizontal gas-liquid annular flow [J].() (化工学报), 2001, 52 (3): 204-208

[13] Qu Weilin, Mudawar Issam. Flow boiling heat transfer in two-phase micro-channel heat sinks (Ⅱ): Annular two-phase flow model [J]., 2003, 46 (15): 2773-2784

[14] Fu Feng, Klausner James F. A separated flow model for predicting two-phase pressure drop and evaporative heat transfer for vertical annular flow [J]., 1997, 18 (6): 541-549

[15] Taitel Y, Dukler A E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow [J]., 1976, 22 (2): 47-55

[16] Kim Sung-Min, Issam Mudawar. Theoretical model for annular flow condensation in rectangular micro-channels [J]., 2012, 55 (2012): 958-970

[17] Fore L B, Beus S G, Bauer R C. Interfacial friction in gas-liquid annular flow: analogies to full and transition roughness [J]., 2000, 26 (11): 1755-1769

[18] Kataoka I, Ishii M, Nakayama A. Entrainment and deposition rates of droplets in annular two-phase flow [J]., 2000, 43 (9): 1573-1589

[19] Milashenko V I, Nigmatulin B I, Petukhov V V. Burnout and distribution of liquid in evaporative channels of various lengths [J]., 1989, 15 (3): 393-401

[20] Tatsuhiro Ueda, Mitsuru Inoue, Seichi Nagatome. Critical heat flux and droplet entrainment rate in boiling of falling liquid films [J]., 1981, 24 (6): 1257-1266

Flow and heat transfer characteristics of annular flow in verticalrectangular narrow channel

CHEN Chong, GAO Puzhen, TAN Sichao, YU Zhiting, CHEN Xianbing

(Laboratory for Fundamental Science in Nuclear Safety and Simulation Technology, Harbin Engineering University, Harbin 150001, Heilongjiang, China)

A mathematical model of annular flow in vertical rectangular narrow channel was developed and experimental verification was performed in order to study flow and heat transfer characteristics of annular flow in vertical rectangular narrow channel. Through numerically solving the mathematical model, pressure gradient, boiling heat transfer and liquid film velocity profile in the annular flow region were obtained. The present model could well predict pressure gradient and boiling heat transfer. The liquid film velocity profile of annular flow in the normal direction was not linear, and liquid film velocity gradient was large in the laminar boundary layer. Rectangular narrow channel size and heat flux had significant effect on liquid film velocity profile. Liquid film velocity increased with increasing heat flux and decreased with increasing channel size. The effect of mass flow rate on liquid film velocity was smaller than the effect of heat flux and channel size, and liquid film velocity decreased with increasing mass flow rate.

rectangular narrow channel; liquid film velocity; annular flow; phase equilibrium; heat transfer; phase change

2014-07-21.

GAO Puzhen, gaopuzhen@hrbeu.edu.cn

10.11949/j.issn.0438-1157.20141094

TL 334

A

0438—1157（2015）02—0537—08

国家自然科学基金项目（50806014）。

2014-07-21收到初稿，2014-09-16收到修改稿。

联系人：高璞珍。第一作者：陈冲（1989—），男，博士研究生。

supported by the National Natural Science Foundation of China (50806014).