一类非局部非线性扩散方程解的全局爆破

裴海杰，李中平，杨丽，杜宛娟

（西华师范大学大学数学与信息学院，四川南充637009）

一类非局部非线性扩散方程解的全局爆破

裴海杰，李中平，杨丽，杜宛娟

（西华师范大学大学数学与信息学院，四川南充637009）

主要研究在Dirichlet边界条件或Neumann边界条件下的一类非局部非线性的扩散方程问题.在适当的假设下，证明解的存在性、唯一性、比较原则、以及解对初边值条件的连续依赖性，并就给定的初边值条件，证明解在有限时刻全局爆破.

非局部扩散；Dirichlet边界条件；Neumann边界条件；全局爆破

1　引言及主要结果

主要研究一类带有Dirichlet边界条件的非局部非线性扩散方程：

和一类带有Neumann边界条件的非局部非线性扩散方程：

其中，J：RN→R是单调递减的光滑径向对称函数，满足

显然函数f在有限时刻t=T处爆破.此时，方程（1.1）、方程（1.2）具有爆破边界条件.过去数十年里，关于扩散模型的研究已取得许多重要成果.比如经典的热方程ut=△u，多孔介质方程ut=△um（其中m＞1），Non-Newton扩散方程但这些扩散模型都是局部的.有关局部扩散爆破研究可参看综述文献［10-12］及专著文献［13-14］.

最近非局部方程

被广泛地应用于对非局部扩散模型的描述.正如在文献［4］中所提及的那样，如果将u（x，t）看作是某种群在点x处t时刻的密度，J（x-y）是该种群从x点跃到y点的概率分布，那么

文献［3］中，C.Cortazar等研究了如下Cauchy问题：

其中，核函数J：R→R为非负的光滑函数，在区间［-1，0］严格递增，［0，1］严格递减，且满足看作是种群在点x处t时刻的密度，为从y点跃到x点的概率分布，那么便是种群从其他地方迁移至x处的速率.与之相应的，为种群迁离x到达其他地方的速率.作者证明了问题（1.4）具有自由边界.

文献［1］中，Bogoya先后研究了如下三个问题：

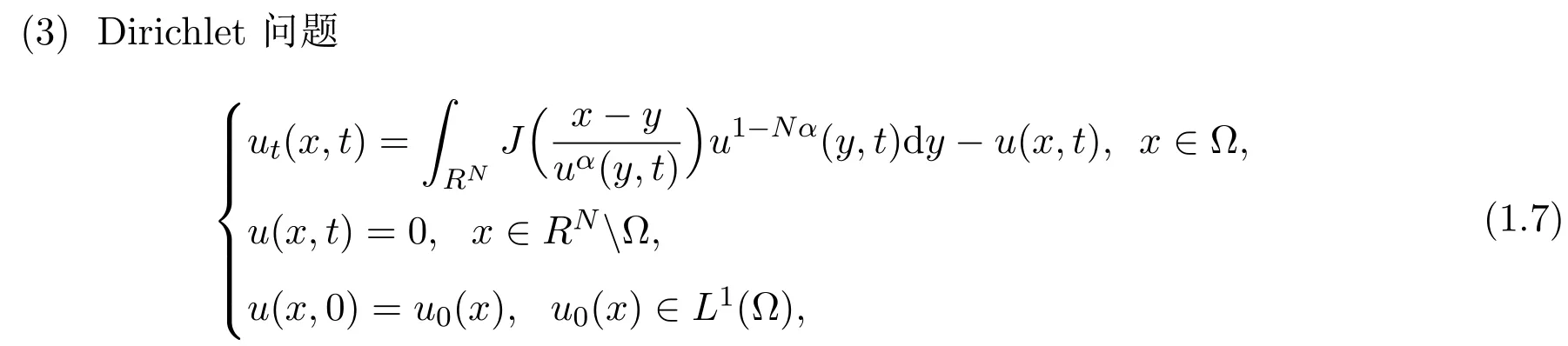
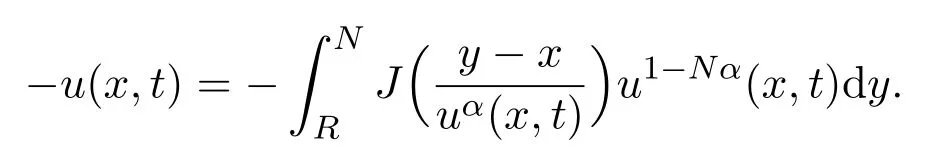
作者证明了对于问题（1.5）：如果初值条件u0（x）是有界的紧支的，那么相应的解存在自由边界.对问题（1.6）：对每一个非负的u0∈L1（Ω），都存在唯一解，使得u∈C（［0，∞）；L1（Ω）），而且特别地，如果且那么方程的解在内将一致有成立.对问题（1.7）：如果函数u0是非负有界的，那么方程的解在内将一致有成立.

Bogoya在后续工作中（见文献［2］），研究了带有爆破边界条件的方程（1.1）与方程（1.2），其中爆破条件f=（T-t）-γ.该文证明了，当γ≤1时，解在有限时刻T全局爆破，并给出了爆破速率.

受上述文献启发，研究带有经典对数形式的爆破边界条件方程（1.1）与方程（1.2），其中f=-ln（T-t）.与幂级数形式相比，对数形式的爆破边界条件，其最大不同之处就在于，对数形式的奇异速率要比幂级数形式的情况慢得多.关于带有对数形式边界流的扩散方程研究可参看［8-9］及其相关参考文献.

现在叙述本文的主要结果.

定理1.1（解的存在唯一性）设g0（x）∈L1（Ω）且是一个非负函数，那么对一切f∈L∞（（0，∞）；L1（RNΩ）），如果存在常数C使得f≥C＞d≥0，那么方程（1.1）与方程（1.2）存在唯一解.

定理1.2（解对初边值条件的连续依赖性）设u（x，t），v（x，t）是方程（1.1）或方程（1.2）的解，相应的初始值为u0及v0，且边界条件分别f1，f2，那么存在一个正常数C：=C（t0）＞0，对某一确定的t0，有下式成立：

定理1.3（比较原则）设u（x，t），v（x，t）是方程（1.1）（或方程（1.2））的的两个连续解，且相应的初始值为u0，v0，以及边界条件分别f1，f2，如果当x∈Ω时u（·，0）≤v（·，0），以及对所有的（x，t）∈（RNΩ）×［0，∞），有f1≤f2成立，那么对一切（RN×［0，∞），有u（x，t）≤v（x，t）.

定理1.4（全局爆破）设u（x，t）是方程（1.1）（或方程（1.2））的连续解，f（x，t）=-ln（T-t），则方程的解在有限时刻全局爆破，且

2　定理证明

定理1.1的证明本文将在Banach空间B=C（［0，t0］；L1（Ω））上证明方程（1.1）解的存在性与唯一性.方程（1.2）解的存在性与唯一性证明与方程（1.1）情形相似，这里不再赘述.

［1］Bogoya M.A nonlocal nonlinear diffusion equation in higher space dimensions［J］.Math.Anal.Appl.，2008，344：601-615.

［2］Bogoya M.Blowing up boundary conditions for a nonlocal nonlinear diffusion equation in several space dimensions［J］.Nonlinear Anal.，2010，72：143-150.

［3］Fife P.Some Nonclassical Trends in Parabolic-like Evolution，in：Trends in Nonlinear Analysis［M］.Berlin：Springer，2003.

［4］Cortazar C，Elgueta M，Rossi J D.A nonlocal diffusion equation whose solution develops a free boundary［J］.Ann.Henri Poincare，2005，6（2）：269-281.

［5］Ignat L，Liviu I，Rossi J D.A nonlocal convection-diffusion equation［J］.Funct.Anal.，2007，251：399-437.

［6］Ignta L，Liviu I，Rossi J D，et al.Decay estimates for nonlinear nonlocal diffusion problems in the whole space［J］.Journal d′Analyse Math´ematique，2014，122：375-401.

［7］Ignat L，Rossi J D，Antolin A S.Lower and upper bounds for the first eigenvalue of nonlocal diffusion problems in the whole space［J］.Differential Equations，2012，252：6429-6447.

［8］Li Z P，Mu C L.Global existence and blow-up analysis for a nonlinear diffusion equation with inner absorportion and boundary flux［J］.Dynamical Systems，26（2）：147-159.

［9］Li Z P，Mu C L.Critical exponents and blow-up rate for a nonlinear diffusion equation with logarithmic boundary flux［J］.Nonlinear Anal.，2010，73：933-939.

［10］Deng K，Levine H A，The role of critical exponents in blow-up theorems：the sequel［J］.Math.Anal.Appl.，2000，243：85-126.

［11］P´erez-Llanos M，Rossi J D.Numerical Approximations for a Nonlocal Evolution Equation［J］.SIAM J.Numerical Analysis，2011，49：2103-2123.

［12］Levine H A.The role of critical exponents in blow up theorems［J］.SIAM Rev.，1990，32：262-288.

［13］Samarskii A A，Galaktionov.V.A，Kurdyumov.S.P，et al.Blow-up in Quasilinear Parabolic Equations［M］.Berlin：Walter de Gruyter，1995.

［14］Wu Z Q，Zhao J N，Yin J X，et al.Nonlinear Diffusion Equations［M］.Singapore：World Scientific，2001.

Global blow-up for a nonlocal nonlinear diffusion equation

Pei Haijie，Li Zhongping，Yang Li，Du Wanjuan

（Department of Mathematics and Information，China West Normal University，Nanchong637009，China）

In this paper，we mainly study a nonlocal nonlinear diffusion equation with Dirichlet boundary conditions or Neumann boundary conditions.Under suitable hypotheses，we will prove existence，uniqueness and the validity of a comparison principle for solutions of these problems，as well as solutions of the problems depend continuously on initial and boundary data.Moreover we will prove that the solution globally blows up in finite time with a given initial and boundary datum.

nonlocal diffusion，Neumann boundary condition，Dirichlet boundary condition，global blow-up elementary method，conjecture

O175.2

A

1008-5513（2015）06-0588-08

10.3969/j.issn.1008-5513.2015.06.006

2015-04-25.

国家自然科学基金（11301419）；四川省教育厅重点项目（13ZA0010，14ZB0143）；西华师范大学大学生科技创新项目（42714081）.

裴海杰（1991-），硕士生，研究方向：偏微分方程.

李中平（1980-），博士，教授，研究方向：微分方程.

2010 MSC：35B44，35B51，35F31