高阶变系数函数方程的非振动解

吴英柱，林全文

（广东石油化工学院数学系，广东茂名525000）

高阶变系数函数方程的非振动解

吴英柱，林全文

（广东石油化工学院数学系，广东茂名525000）

给出一类高阶非线性函数方程的一些新的非振动准则，并且给出了在差分方程中的若干应用，结果改进和推广了近期文献的某些结果.

函数方程；非线性；振动；非振动解

1　引言

考虑高阶非线性变系数函数方程：

近年来，差分方程和函数方程的振动性成为数学工作者研究的热门课题［1-13］，得到各类高阶函数方程解的振动准则.但研究非线性函数方程的文献比较少，用非迭代方法研究函数方程的非振动性的文献则更少.最近，文献［1-2，13］研究了方程：

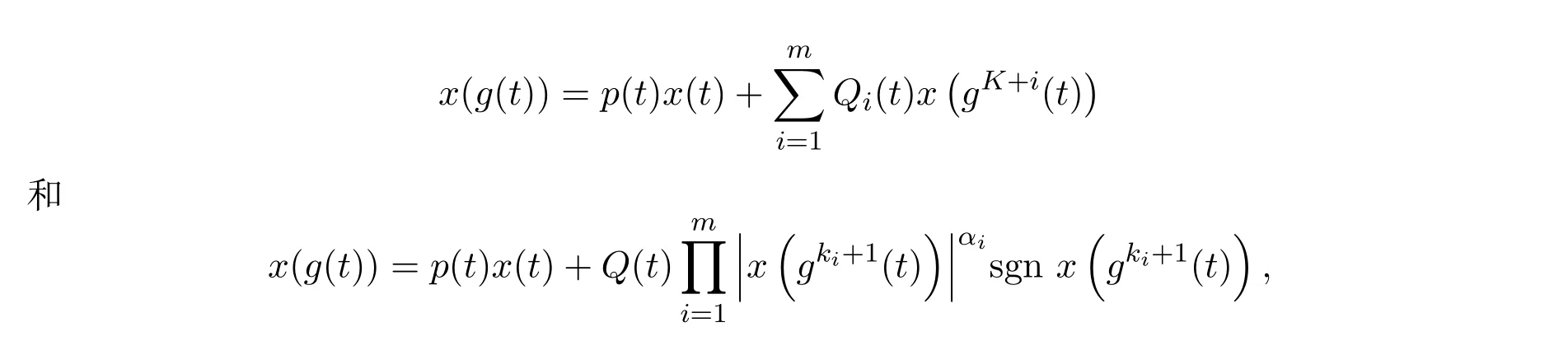
得到了一系列结果.

本文受文献［11］启发，进一步研究非线性函数方程（1）解的非振动性，沿用文献［1，13］的方法，得到了一些新的结果.这些结果全面推广了文献［13］的结果，部分推广了文献［1］的结果，推广了文献［4］的定理和文献［5］的定理2.2，改进了文献［5］的推论2.

2　主要结果及证明

定理2.1假设p（t）＞0，Qi（t）∈R，g（t）＜t，且存在正函数A（t）和一个正整数T，使得

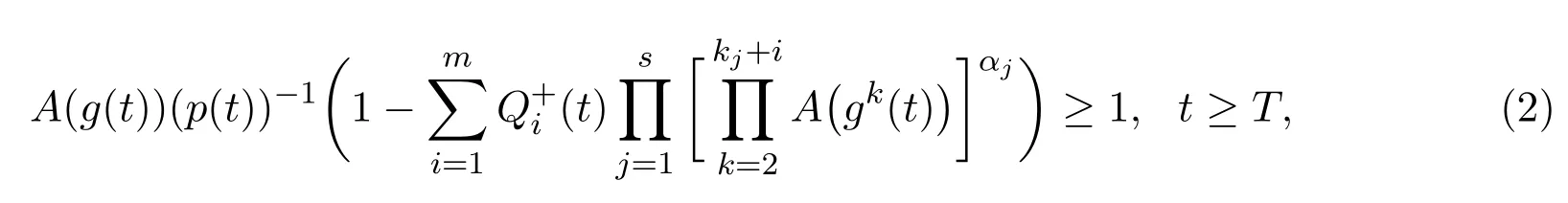
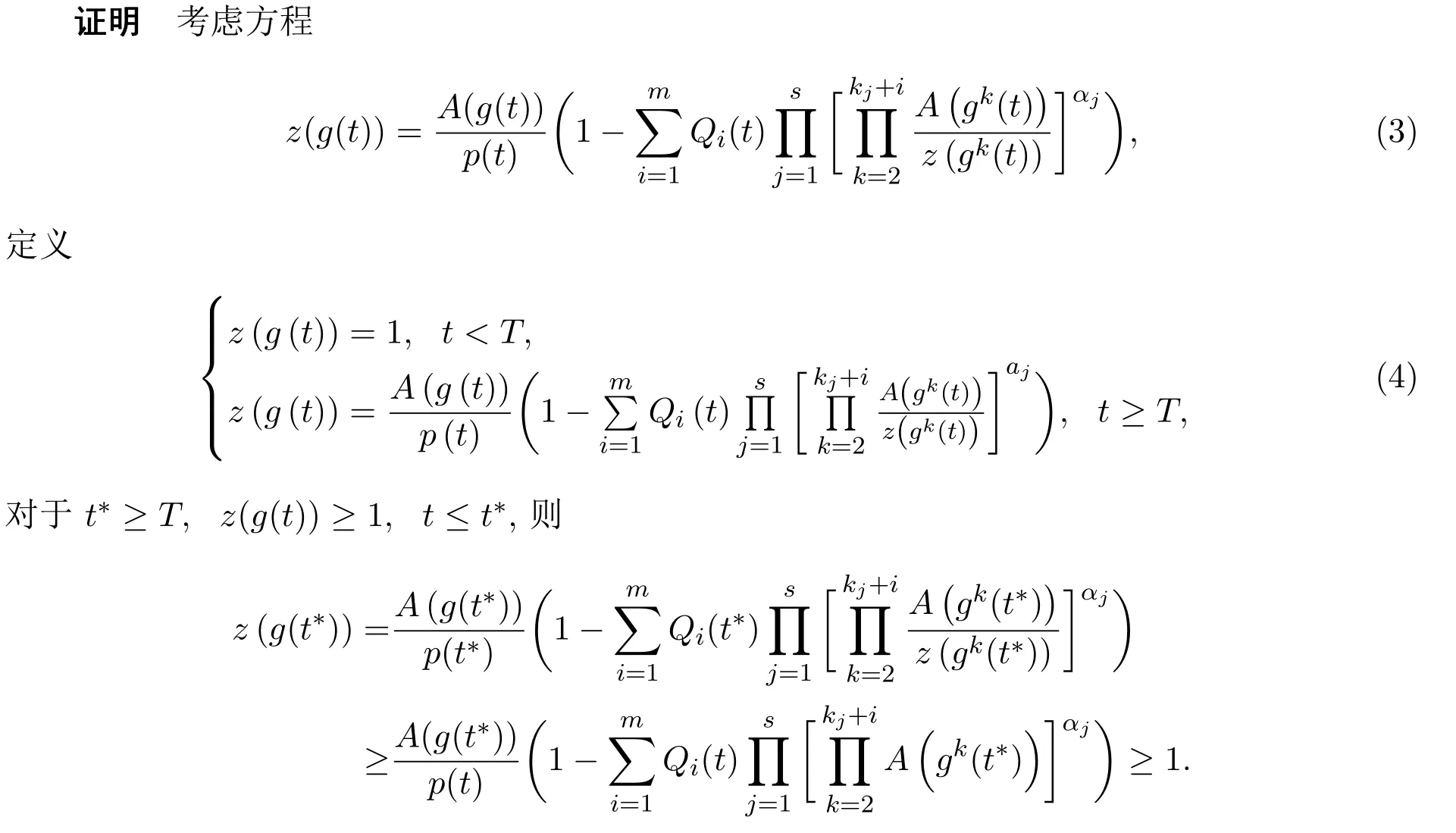
推论2.1如果存在u＞0，使得

推论2.2如果

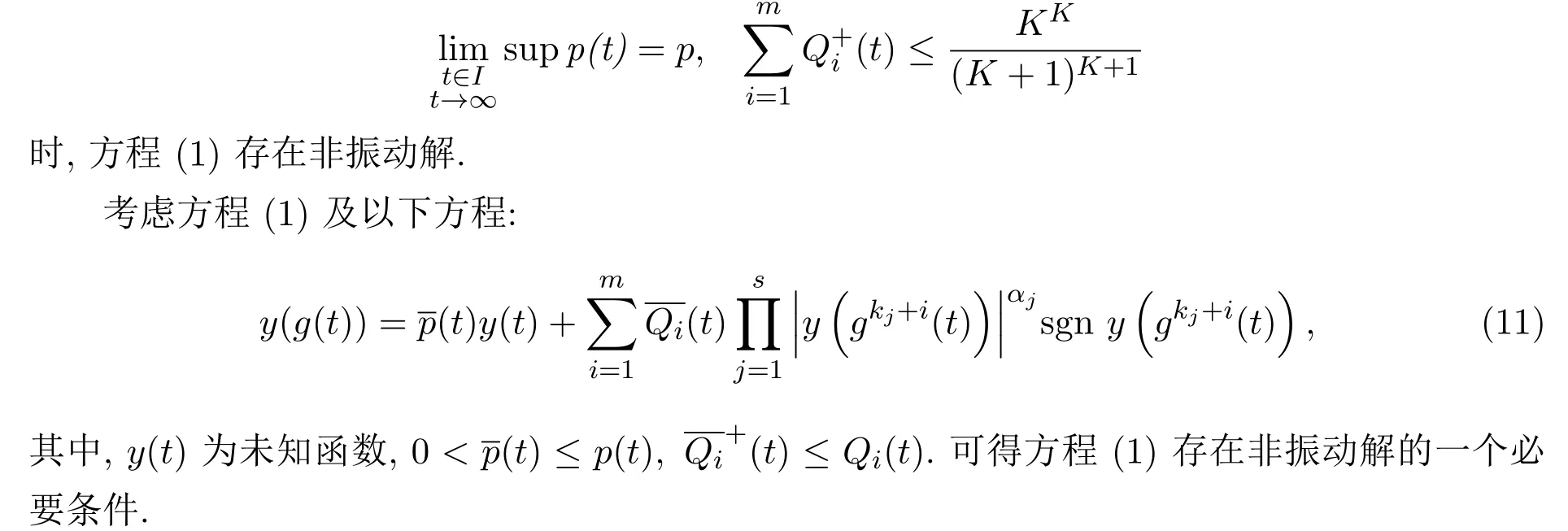
3　应用

由于离散变量的差分方程和具有连续变量的差分方程作为方程（1）的特殊情形.对于g（t）=t-τ，τ∈R+，I∈R+的情形，方程（1）可化为具有连续变量的差分方程：

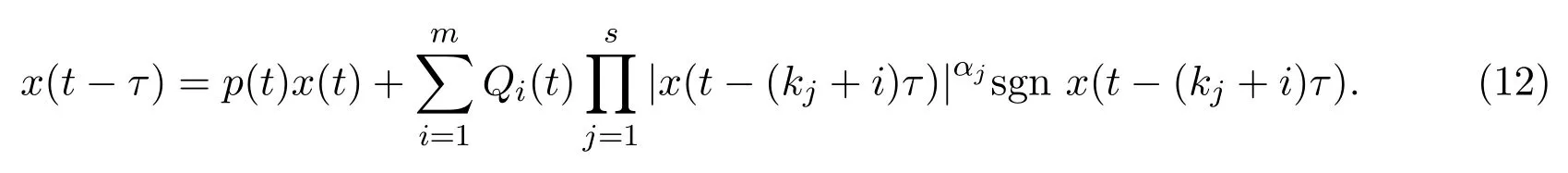
由定理2.1和定理2.2，易得以下定理：

定理3.1若存在函数A（t）＞0，p（t）＞0，Qi（t）≥0，使得

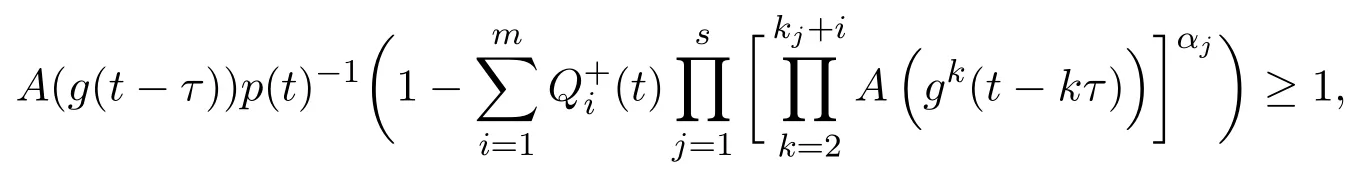
则方程（12）存在非振动解.

同理，考虑以下无穷时滞的差分方程我们易得以下结果：

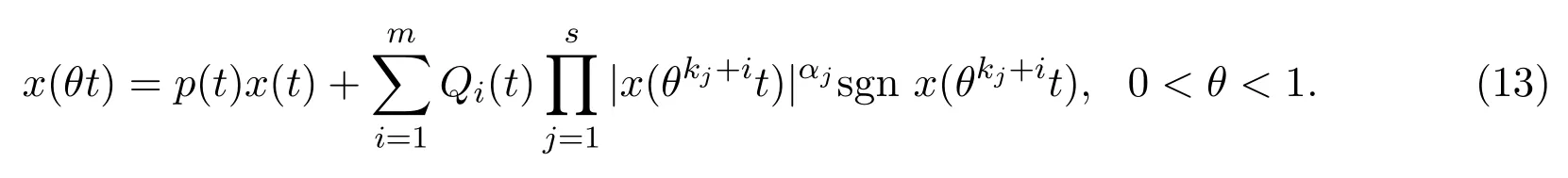
定理3.2若存在函数A（t）＞0，p（t）＞0，Qi（t）≥0使得

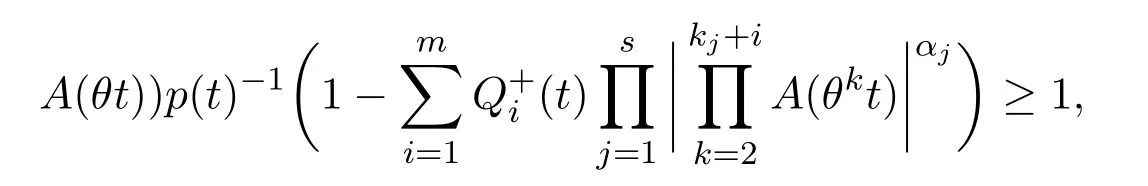
则方程（13）存在非振动解.

［1］周勇，俞元洪.变系数函数方程解的振动性［J］.系统科学与数学，1999，19（3）：348-352.

［2］周勇，刘正荣，俞元洪.变系数函数方程解的振动准则［J］.应用数学学报，2000，23（3）：414-419.

［3］Domshla Y.Oscillation properties of linear difference equations with continuous time［J］.Differential Equations and Dynamical Systems，1993，4：331-324.

［4］Golda W，Werbows J.Oscillation of linear functional equations of the second order［J］.Funkcialaj Ekvacioj，1994，37（2）：211-228.

［5］Nowakowska W，Werbowski J.Oscillation of linear functional equations of the second order［J］.Arch.Math.，1995，31：251-258.

［6］Nowakowska W，Werbowski J.Oscillatory behavior of solutions of functional equations［J］.Nonlinear Anaysis，2001（44）：756-775.

［7］Zhang B G，Choi S K.Oscillation and nonoscillation of class of functional equations［J］.Math.Nathr.，2001（227）：159-169.

［8］Shen J N，Stavroulakis，I P.An oscillation criteria for second order functional equations［J］.Acta.Math.Sinica.，2002，22B（1）：56-62.

［9］张孝理，罗治国.高阶线性泛函方程的振动性［J］.应用数学学报，2003，26（1）：186-188.

［10］罗治国，申建华.线性泛函方程解的振动性的新结果［J］.系统科学与数学，2003，23（4）：508-516.

［11］林全文，全焕，廖思泉，等.高阶变系数函数方程的振动性［J］.数学的实践与认识，2009，39（12）：244-249.

［12］Lin Quanwen，Chen Renlian，Dai Lina.Oscillatory behavior of solutions to higher order linear functional equations［J］.Journal of Biomathematics，2011，26（1）：9-16.

［13］伍思敏，戴丽娜，林全文.高阶泛函方程解的非振动准则［J］.数学的实践与认识，2013，43（20）：280-284.

Nonoscillation criteria of higher order functional equations with variable coefficients

Wu Yingzhu，Lin Quanwen

（Department of Mathematics，Guangdong University of Petrochemical Technology，Maoming 525000，China）

This paper discusses oscillation of solutions to high-order variable coefficient functional differential equations，new results of non-oscillation criteria are obtained.Some applications of differential equations are given.Our results improve some of the known results in the literature.

functional equations，nonlinear，oscillation，solutions of non-oscillation

O175.1

A

1008-5513（2015）06-0575-06

10.3969/j.issn.1008-5513.2015.06.004

2015-06-10.

国家自然科学基金（10671155；10112021）；广东茂名市科技计划资助项目（2014050），广东石油化工学院自然科学研究基金（513021）.

吴英柱（1978-），硕士，讲师，研究方向：微分方程与动力系统研究.

2010 MSC：34A34