接触运动传递机构的合成运动问题思考

马银华　杨庆国

摘要 针对点的合成运动分析中的两类接触运动传递机构问题，基于其特点与解题方法的分析，指出了其中第二类常见问题分析方法的局限性。为此，设计了一类非常规的接触运动传递机构问题，并分析了其求解方法。本文指出，现有的常规分析方法不适用于非常规问题，想要简单有效地解决这类问题，须突破对于“动点”、“动系”选择方法的传统认识，在分析思路和方法上进行创新。本文关于非常规问题的分析方法，强调了动系选择的灵活性，这对于丰富合成运动的求解方法以及提高学生分析问题、解决问题的能力，具有重要意义。

关键词 接触运动传递机构 合成运动 动系

中图分类号：TP23 文献标识码：A DOI：10.16400/j.cnki.kjdks.2015.08.076

Thinking of Synthetic Movement Contacting

Motion Transmission Mechanism

MA Yinhua， YANG Qingguo

（School of Civil Engineering and Architecture， Chongqing Jiaotong University， Chongqing 400074）

Abstract For two types of contacts motion transfer mechanism synthesis Kinematics question of， based on the analysis of its characteristics and problem-solving approach， pointing out the limitations of the second class of common problems where analysis methods. For this reason， the design of a class of unconventional touch movement transmission mechanism problem， and analyzes its solving method. This paper points out， existing conventional methods do not apply to unconventional problems， they want a simple and effective way to solve such problems， must break the "fixed point"， the traditional understanding of "dynamic system" selection method， the analysis of ideas and methods innovation. Unconventional analysis method on the issue， emphasizing the flexibility to select dynamic system， which for the ability to enrich the movement Solution synthesis and improve the students to analyze and solve problems， and has great significance.

Key words contacting motion transfer mechanism; synthetic movement; dynamic system

运动学作为理论力学的三大教学内容之一，是机械类专业后续课程如机械原理的重要基础。其中，点的合成运动是运动学的教学重点和难点。在实际工程问题中，点的合成运动知识应用十分广泛，在研究约束联系机构的各刚体之间运动关系时，可以发挥重要的作用。点的合成运动方法并非只是一种“瞬时分析法”，它也可以对运动机构进行“全程分析”。①相比于以几何和高等数学为基础的点（刚体）的运动方程求解速度、加速度方法，点的合成运动方法往往可以使问题的分析和求解更加简便。

有一类点的合成运动问题非常常见，即接触运动传递机构问题，它是机械工程中的常见类型。在教材②③中，接触运动传递机构的点的合成运动问题很多，概括起来，这类机构可分为两种情况：第一类是有不变的接触点，第二类是没有不变的接触点。本文针对这两类情况，总结了现有教材或资料中常见问题的特点及分析方法，同时基于第二类情况分析方法存在的局限性，思考提出了一种非常规问题，并给出了简单、可行的求解分析方法，以便教师和学生深入理解、灵活运用点的合成运动知识，为工程中可能遇到的这类非常规问题提供一种有效解决方案。

1 常见问题的特点及其分析方法的局限性

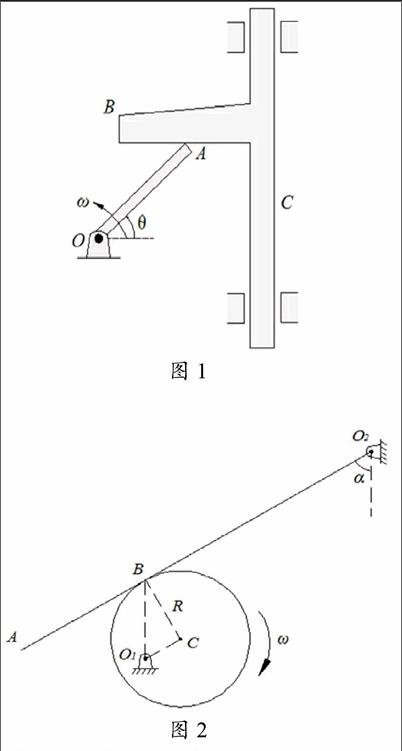
接触运动传递机构的第一类常见问题，是存在不变的接触点，即接触点始终为某一刚体上相对位置不变的点（如图1）;第二类常见问题，是不存在不变的接触点，即两个刚体的接触点都会随时间而改变，接触点在任一刚体上的相对位置都不是固定的（如图2）。

对于第一类问题，学生易于接受的、最简单的方法就是选择刚体上不变的接触点为动点，动系固结于另一刚体上，这样容易确定相对运动的轨迹，便于合成运动分析。对于第二类问题，由于接触点对于任一刚体来说都不是相对位置固定的点，通常的观点认为：不应选择接触点为动点，否则会因相对运动轨迹不清楚，而给速度分析尤其是加速度分析造成很大的困难。因此，教学中建议选择非接触点为动点，以动点相对于动系的相对运动轨迹易于确定为基本原则。面对这样的问题，要求学生在充分理解动点、动系选取原则的基础上，仔细观察和分析机构的运动特点，选定合理的动点及相应的动系。这对于初学的学生来说，是有一定难度的。

诸如图2所示第二类问题的例题或习题，在教材和相关教学参考资料中有很多，我们可以发现这些题都有相似之处，其中一个接触刚体要么是圆轮，要么是半圆的凸轮等。它们共同的特点就是，总能在圆形刚体上找到一个动点，使得其到另一刚体（或刚体的某一点）的距离始终保持不变。如图2所示，由于运动过程中偏心轮的轮心C点到O₂A杆的距离始终为半径R，故选择C点为动点，动系固结于O2 A杆，这样相对运动轨迹为平行于O₂A杆的直线运动，合成运动分析就很方便。

对于具备上述特点的第二类接触运动传递机构，学生们只要掌握了以圆形刚体的圆心为动点的解题关键，举一反三，其他同类特点的问题都可以采用相同方法迎刃而解。然而，这种分析方法却存在严重的局限性，那就是，它只能解决具备上述特点的问题。对于不具备这种特点的第二类接触运动传递机构，显然，前述分析方法并不适用，而要解决这类问题，若采用建立运动方程的方法，则会相当困难。现有教材中，都只是针对类似图2所示机构的常规问题展开研究，在这样的教学设计下，作者认为并不利于提高学生分析问题和解决问题的能力，难以培养学生的创新能力。

2 非常规问题的思考及分析方法

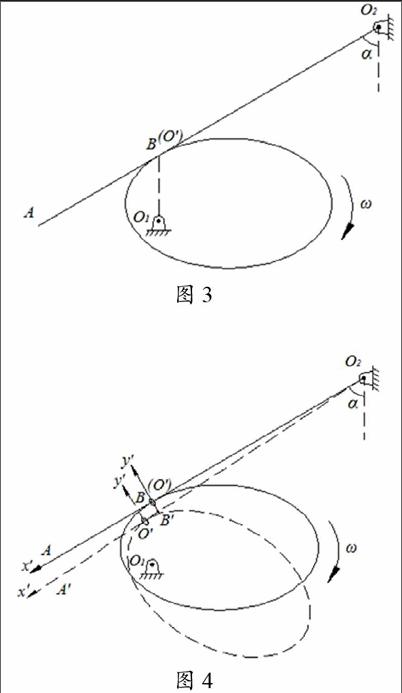
鉴于上述常规问题分析方法存在的局限性，作者设计了一种非常规的第二类接触运动传递机构。如图3所示，当图2中的圆轮变成非圆轮（如椭圆轮或其他不规则形状刚体）后，非圆轮刚体中无法找出一个到O2 A杆距离始终保持不变的动点。

问题设计：图3机构与椭圆轮在点接触，如已知椭圆轮的角速度，（铅垂），求图示瞬时的杆的角速度？

按照接触运动传递机构问题的常规分析方法，是不建议选择接触点作为动点的，同时又由于在椭圆轮中找不到一个与杆距离保持不变的点，故学生们会感到点的合成运动知识在该题中无法应用。如果从几何的角度，利用数学推导求杆的运动方程继而求导得到杆件的角速度，这样又可能缺乏一些必要的求解条件，并且推导过程会非常复杂繁琐（如果是其它不规则形状的刚体，则分析求解会更加困难）。

实际上，这种问题仍然可以利用合成运动的知识来求解，只是我们需要改变已经形成的常规的动点、动系选择方法，寻求一种新的思路。下面，我们将采用“自构建动系法”，来分析这个问题。在此之前，首先对“自构建动系法”进行说明。在选择动系时，并不一定要将其固结于题目中某一实际存在的运动刚体之上，在不违背动点、动系选择的原则下，动系完全可以灵活选择。比如，在选定动点后，为了便于相对运动轨迹的直观确定，可以将动系固结于一个我们自行构建的虚拟运动刚体上，该刚体的运动形式和运动条件可以自行设定。也就是说，我们可以根据需要自行构建一个动系，并人为设定该动系的运动特征。但前提是，在自构建动系下，动点的相对运动轨迹易于判定，并能够获得足够的求解已知条件。

上述问题的求解分析过程如下：

（1）动点、动系的选择。

动点：杆上与椭圆轮接触的B点（该方法已突破这类问题的常规动点选择方法）。

动系：首先虚拟一个微小套环（小到可看作一个点），让其套在杆件与椭圆轮的接触点处，并随着机构运动而始终位于两物体的接触点（套环会相对于杆件与椭圆轮都有相对运动）。然后，以微小套环为原点，建立动系，如图4所示。最后，令动系跟随点移动的同时还转动，并且设定动系转动的角速度与杆的角速度始终相同，即动系的轴始终与杆重合（该动系建立方法突破常规，常规方法中，当动点选择在杆件上时，动系固结于椭圆轮）。

定系：固结于地面。

（2）运动分析。

基于上述动点、动系选择方法，三种运动的形式和轨迹（特别是相对运动轨迹）将十分清楚。

绝对运动：以为圆心，为半径的圆周运动。

相对运动：沿杆方向的直线运动（如图4，动点运动后的位置始终在动系轴上）。

牵连运动：动系的运动为平面运动。

（3）速度分析。

建立速度合成定理：……（1）

其中，绝对速度的大小未知（与待求量杆件的角速度有关）、方向垂直于杆;相对速度的大小未知、方向沿杆;牵连速度即为套环的绝对速度（图3瞬时，动系上与动点重合的点为微小套环），其大小方向均未知。

以套环为动点，动系固结于椭圆轮上，再次利用点的合成运动知识，可以求出套环的绝对速度（也就是式1中的）：  ……（2）

其中，为第二次合成运动分析中的牵连速度，即椭圆轮上与动点（套环）重合点的速度（该点绕作圆周运动），其大小、方向均可由题目的已知条件确定;为第二次合成运动分析中的相对速度，由于套环相对于椭圆轮的运动轨迹为椭圆周线，故的方向沿椭圆切线即杆方向，但其速度大小未知（若知道椭圆在点处的曲率半径，实际上可建立相对速度大小与曲率半径、杆角速度之间的关系，读者可自行推导）。

联立式（1）、式（2）得到：  ……（3）

综上分析，式（3）中虽有3个未知量，但和这两个未知矢量的方向都沿杆方向，而另一位置矢量的方向垂直于杆，故作速度合成矢量图（本文略）后，将矢量式（3）在垂直于杆的方向投影，即可求得的大小及方向。进而，杆的角速度可求。

（4）总结。

本题的分析不同于常规思路，关键是采用自构建动系法，灵活的建立了动系，使得相对运动轨迹十分清晰。虽然两次运用了点的合成运动分析，但每一次的分析思路都非常清楚，利用的都是现有的合成运动理论，而且求解过程并不复杂。与解决这类问题的其他方法相比，采用上述方法将使问题的求解过程极大地简化。自构建动系法同样可以应用于其他常规问题的求解，这对于丰富合成运动的分析方法和解题手段，具有重要作用和意义。

3 结语

动点和动系的选择，是求解合成运动问题的关键，在点的合成运动教学中，对“动点”选取和“动系”建立方法的理解，不能仅停留在传统的一般认识上。对于非常规类型的接触运动传递机构问题，须突破已有的思维定式，在分析思路和方法上进行创新。动系的灵活选择非常重要，自构建动系法在非常规复杂问题中的应用，可为这类问题的合成运动分析提供简单、有效的解决方案。

注释

① 冯立富，郭书祥，李颖.点的合成运动与“全程分析法”[J].空军工程大学学报（自然科学版），2002.3（5）：86-87.

② 哈尔滨工业大学理论力学教研室.理论力学I[M]（第7版）.北京：高等教育出版社，2009.

③ 西南交通大学应用力学与工程系.工程力学教程[M]（第2版）.北京：高等教育出版社，2009.