整合《数学分析》课程 培养学生的综合分析能力
2015-10-14马建珍刘俊先
马建珍,刘俊先,田 亚
整合《数学分析》课程 培养学生的综合分析能力
马建珍,刘俊先,田 亚
(邢台学院数学与信息技术学院,河北邢台 054001)
通过对《数学分析》课程的恰当整合,使之理论线条更加清晰,从中培养学生的综合分析能力,达到更好的教学效果。
数学分析;整合;综合分析
数学分析是数学专业最重要的基础课程之一,对数学专业后继课程(如复变函数论、常微分方程、实变函数、概率论与数理统计等)的学习和研究影响甚大。它不但是众多学科(如物理、计算机、经济数学等)的重要基础和有力工具,而且对培养学生的逻辑思维能力、夯实学生的数学基础、加强学生的基本功训练都具有十分重要的功效。学生学好这门课程,就奠定了大学阶段学好数学的基础,也是开创数学学习良好局面的关键。根据课程的进度,引导学生恰当地整合相关知识,可以使学生在学习新知识的同时,对与之相关的知识有更深入透彻的理解,在此过程中培养学生的综合分析的能力。
1 同一知识板块内容的整合
1.1 一元函数极限归纳
在学完一元函数的极限理论之后,引导学生对一元函数极限的类型和定义进行归纳总结。
一元函数极限的类型共有24种,分为极限过程和极限结果两部分。具体为:
把6种极限过程和4种极限结果相结合,可得到24种极限形式。若用精确的数学语言去定义,要用两个字母(等)去刻画。即任意给一个量(等),对极限结果作出要求,然后用另一个字母(等)表述极限过程,要满足极限结果的要求,自变量必须变化到某种程度。学生能理解这些量之间的关系,就很容易写出它们的定义。例如:
上述24种极限都有其否定形式,故又有24种否定的定义。对于上述极限定义,其否定的定义具体为:
仿照上述极限定义及其否定形式,可指导学生把24种全部写出。
在学完二元函数的极限之后,可以引导学生来比较一元函数的极限与二元函数的极限有哪些本质的区别。对于二元函数,极限类型更多,例如:
经过这样的练习过程,不仅可使学生能精确地写出极限定义,同时通过分析各种不同极限之间的异同,加深了对极限概念的理解,提高了综合分析能力,也为下一阶段的学习打好极限理论的基础。
1.2 求不定积分和定积分
在学完一元函数积分学之后,引导学生对积分方法进行归纳总结。求不定积分的方法有:(1)利用基本积分公式;(2)换元积分法;(3)分部积分法;(4)有理函数的积分法;(5)无理根式积分法;(6)三角函数的积分法。
求定积分除了有与上述不定积分相对应的积分方法外,还有牛顿-莱布尼茨公式(原函数可通过求相应的不定积分来求出,在理论上此公式把不定积分与定积分联系了起来)。在讲解定积分的内容时,引导学生联系不定积分的相应内容,透彻理解它们之间的关系,如:不定积分的换元积分法换元后一定要作变量还原,因为不定积分所求的是被积函数的原函数族,理应保留与原来相同的自变量;而定积分的计算结果是一个确定的数,一旦得到了用新变量表示的原函数后,不必作变量还原,而只要用新的积分限代入并求其差值就可以了。不定积分的换元积分法分为第一换元积分法和第二换元积分法,而定积分的换元积分法则只有一个换元积分公式,两个不同方向的使用恰好对应不定积分的两种换元积分法。
通过对一元函数积分学内容进行整合,提高了学生的综合分析能力,学生会明显感觉积分内容更加条理,解题规律和积分方法非常类似,积分方法更加清晰,解题的难度大大降低,提高了学好积分内容的信心,也为之后的学习多元函数积分学打下坚实的基础。
1.3 求重积分和曲线积分、曲面积分
1.3.1 二重积分与三重积分
学习二重积分时,引导学生与定积分相比较,会发现二重积分的定义、可积条件、性质与定积分基本上是平行的,是定积分在二维空间的推广。二重积分的计算采用累次积分法,与定积分有极其密切的联系。三重积分的定义、可积性、性质与二重积分是完全平行的,二者只是形式上的差别,没有本质的区别。
直角坐标系下二重积分的计算:根据积分区域的特征,分为型区域和型区域,结合被积函数的特点化为累次积分。直角坐标系下三重积分的计算:根据积分区域的特征,分为“先二后一法”或“先一后二法”。较常见的是“先一后二法”。二重积分、三重积分的变量变换:根据积分区域和被积函数的特征进行适当的变量变换,以简化积分区域或被积函数,二重积分的重点是极坐标变换。三重积分的重点是柱面坐标变换和球面坐标变换。而柱面坐标变换是采用“先一后二法”,其中的二重积分是采用极坐标变换。
经过上述比较分析,可以发现二重积分的计算是三重积分的基础(例如:二重积分的极坐标变换与三重积分的柱面坐标变换的关系),而二重积分的计算又是以定积分的计算为基础的。如果有夯实的定积分的基本知识,学生会发现重积分并没有想象的那么难学。引导学生在学习过程中不断整合相关的理论知识,既提高了综合分析能力,也加深了对新知识的理解,提高了解题能力。
1.3.2 曲线积分
平面上的第一型曲线积分也是定积分的一种推广。它将轴线段上的积分推广到平面曲线段上的积分,或者说,定积分是平面上第一型曲线积分的特殊情况。第二型曲线积分主要是讨论向量函数,它在场论中具有多种不同的物理意义。
定积分的应用中所用的微元法可以推广到第一型曲线积分的应用中。例如,对于定积分在物理上的应用,利用微元法讨论了液体静压力、引力、功以及平均功率等的计算。通过类似的思想方法,也可以讨论第一型曲线积分在物理上的应用。例如:设有线密度的平面曲线段,则
(2)对轴与轴的静矩分别为

两类曲线积分的计算都是化为定积分来计算,故基础还是定积分的计算。
1.3.4 曲面积分
第一型曲面积分是二重积分的推广,它将坐标平面上有界区域推广到中的有界光滑曲面,即坐标平面上有界区域是中的一个特殊的光滑“曲面”。 第一型曲面积分的有关性质与二重积分是完全平行的,二者只是形式上的差别,没有本质的区别。第二型曲面积分是向量函数在曲面上的积分,它是力学、电学等学科的重要的数学工具。
两类曲面积分的计算都是化为二重积分来计算,故基础还是二重积分的计算。
1.3.5 格林公式、高斯公式和斯托克斯公式
格林公式是沟通区域上的二重积分与该区域边界(封闭曲线)上的曲线积分之间的桥梁。奥-高公式是沟通三重积分与第二型曲面积分之间的桥梁。斯托克斯公式是沟通第二型曲面积分与空间第二型曲线积分之间的桥梁。这两个公式在场论中占有重要的地位。
上述三个公式又把看起来好似没有关联的不同的重积分、线积分和曲面积分联系起来。
本部分内容丰富,计算公式多,且会用到一元函数积分学及空间解析几何的一些相关基础知识,综合性强,学生普遍感觉难学,不易掌握,很多学生会用错计算公式导致计算错误。通过整合本部分内容,使内容的线条、知识间的相互关系更加清晰,学生更易掌握。例如:直角坐标系下的二重积分与第二型曲面积分在书写形式上比较接近,如何区分它们呢?如果能注意以下几点,便不难区分:
(1)二重积分的被积函数是二元函数,第二型曲面积分的被积函数一般是三元函数;
(2)二重积分的积分区域是平面区域,第二型曲面积分的积分区域是空间曲面;
(3)二重积分的积分区域,不需要指定它的侧。第二型曲面积分的积分区域,都要指定它的侧。
如果被积函数形式上是二元(一元或常值)函数,且积分区域为相应坐标平面上的平面区域,同时取正侧,则在该曲面上的第二型曲面积分与对应的平面区域上的二重积分一致。例:取的上侧,则曲面积分与二重积分相同,其中。
2 不同知识板块内容的整合
2.1 一元函数与多元函数相类似题目的整合
在讲解多元函数微分学知识时,以二元函数为例,其连续性、偏导数存在性及可微之间的关系和一元函数对应的连续、可导及可微之间的关系是否类似,哪些性质是类似的,又有哪些不同?这些内容在讲解多元函数微分学时是需要特别强调的。
对于一元函数来说,函数在一点可导与可微是等价的;可导一定连续,但连续不一定可导。对于二元函数来说,偏导数连续一定可微,反之不一定成立;可微一定连续,反之不一定成立;满足可微时偏导数一定存在,反之不一定成立;;而连续和偏导数存在二者之间没有必然的关系。例如
2.2 一元函数的一些结论可推广多元函数
2.2.1 极值的必要条件
2.2.2 可微定义
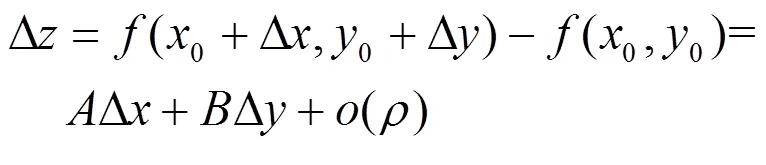
二元函数的可微定义与一元函数的可微定义是完全类似的,可以看做是一元函数的可微定义的推广。
类似上述内容,在教学中,可让学生在课下试着完成,之后再在课堂上结合具体的教学内容来讲解,尤其是第三学期学习多元函数的微积分,学生已经有一定的理论基础,又完整地学完了一元函数的微积分学,通过让学生多做这样的练习来培养学生的综合分析能力。
通过课程内容的恰当整合,就可以使知识点由多变少,把教材由厚变薄,使数学分析课程的整体结构更加清晰。并使得学生能透彻理解相关知识同时可使学生取得更高效的学习效果,为后续专业课的学习打好数学分析的理论基础。
[1]杜其奎,等.数学分析精读讲义[M].科学出版社,2012.6.
[2]刘三阳,李广民.数学分析十讲[M].科学出版社,2011,6.
[3]武忠祥,等.历届数学考研试题研究[M].西安:西安交通大学出版社,2005.
[4]明清河.数学分析的思想和方法[M].济南:山东大学出版社, 2004.
[5]刘玉链,傅沛仁.数学分析讲义(第三版)[M].北京:高等教育出版社,2001.
[6]华东师范大学数学系.数学分析(第三版)[M].北京:高等教育出版社,2001.
[7]刘三阳,等.各类考研数学全真试题与解答[M].西安:西安电子科技大学出版社,2001.
[8]郝涌,李学志,陶有德.数学分析选讲[M].北京:国防工业出版社,2010.
2014-12-21
[科研项目]2013年邢台学院科研项目:基于综合分析能力培养的《数学分析》课程的整合研究.项目编号:XTXY13YB103
马建珍(1969-),女,毕业于河北师范学院,副教授,主要从事数学教育与研究.
O17
A
1672-4658(2015)02-0173-03
