一种基于QR分解的稳健干扰对齐算法

谢显中 张森林 肖正瑛



一种基于QR分解的稳健干扰对齐算法

谢显中*张森林 肖正瑛

(重庆邮电大学个人通信研究所 重庆 400065)

大多数干扰对齐算法都假定发送端可以获得理想的信道状态信息(CSI)，由于信道估计误差、反馈延迟等原因，实际通信系统中CSI往往是有误差的。为此，该文提出一种基于QR分解的稳健干扰对齐算法。对含有误差的联合接收信号进行基于QR分解的预处理，消除一半有误差的干扰；然后在有误差的等效信道联合矩阵下，充分考虑信道误差和干扰的影响，通过最小化发送端泄漏到非目标接收端的干扰信号功率来设计预编码矩阵，并基于最小均方误差(MMSE)准则来设计干扰抑制矩阵。最后，在理想CSI和误差CSI的情况下，通过实验仿真，证明了该算法有效地提高了系统性能。

无线通信；稳健干扰对齐；信道估计误差；QR分解；系统性能

1 引言

干扰对齐(Interference Alignment, IA)技术[1,2]由于其能够有效地消除同频道干扰，受到了广泛的关注。目前，大多数干扰对齐算法[3,4]都是基于完美的信道状态信息(Channel State Information, CSI)。由于信道估计误差、反馈延迟等原因，实际通信系统中CSI往往是有误差的，使得接收端不能完全抑制来自其他发送端的干扰，造成系统性能下降。

最近，一些文献开始对不完美CSI下的干扰对齐方案进行研究。针对误差CSI的情况，文献[5]通过卡尔曼信道预测来设计预编码矩阵和干扰抑制矩阵，有效地提高了信道容量。文献[6]给出了基于对称最小均方误差(Minimum Mean Square Error, MMSE)算法的稳健干扰对齐算法，不需要计算拉格朗日乘子，并考虑了用户的公平性。文献[7]分析了在误差CSI时，对称MMSE干扰对齐算法的误码率性能。文献[8]研究了基站仅知有噪CSI时系统平均互信息量可达到的上下限，表明相比基站间没有进行协作处理，采用干扰对齐技术可以获得更好的性能。文献[9]提出了一种仅仅知道本地有噪CSI时的功率控制和收发方案设计的迭代算法。文献[10]针对误差CSI，利用重构的格型码对干扰信号进行重构，克服了准静态信道时干扰对齐难以实现的问题，提出了一种稳健的格型干扰对齐算法，但接收端需要两步解码。文献[11]提出了一种稳健的最小干扰泄露算法，提高了在具有信道误差时，普通的最小干扰泄露算法的性能。文献[12]分析了在具有信道误差时误比特率(Bit Error Rate, BER)受到的影响，最后提出了一种比特加载算法的自适应传输方案。

文献[5~9]通过最小化发送信号和接收信号的差异来提高信干噪比，但没有区别对待误差项和干扰项。文献[10]的处理过于复杂，文献[11]在最小化干扰项和误差项空间维度时，没有考虑如何提高信号本身的传输质量。文献[12]使用比特加载算法，以最小化误比特率为目标，自适应地选择干扰对齐算法，改善了传统干扰对齐算法的BER性能，但是并没有充分考虑如何减弱干扰。此外，文献[13]分析了采用迫零算法时，信道估计误差对BER的影响。文献[14]对联合信道矩阵进行QR分解，对小区间干扰和小区内干扰进行了对齐，取得了良好的性能。但文献[13,14]并没有提出适用于实际通信系统的稳健干扰对齐算法。

针对以上文献算法性能对干扰和信道估计误差灵敏度高的问题，本文提出了一种基于联合信道QR分解的稳健干扰对齐算法。最后进行了实验仿真，结果表明，相对于其他稳健算法而言，无论是理想CSI还是误差CSI，本文算法都具有一定的性能优势。

2 系统模型与QR分解

类似文献[11]，本文考虑用户MIMO干扰信道，每个发送端的天线数为t，每个接收端的天线数为r，每个用户对应的自由度为，此处的自由度代表每个用户能使用的独立数据流的个数。为了让系统自由度达到最大值，即min(r,t)/2，那么每个发送端所提供的信号空间的维数应该相等，故此处不妨设，并假设在同一时刻同一频率上的各个发送接收对之间的信道是平坦衰落的，且信道系数独立同分布。在一个特定的时频资源上，接收端的接收信号可以表示为

其中维数为r×t的和分别是发送端和发送端到接收端的信道矩阵。维数为t×d的和t×d的分别是发送端和发送端上对应于接收端和的预编码矩阵，且满足,。维数为d×1的是接收端的下行数据矢量信号，且满足功率约束。维数为r×1的是均值为0，方差为1的加性高斯白噪声，且。

干扰对齐往往要求完美的CSI，但在实际通信系统中，发送端得到的CSI常常是有误差的。为了构建稳健的干扰对齐算法，此处引入信道误差变量,表示真实的信道矩阵，表示具有误差的信道矩阵，并且假设的元素是服从均值为0，方差为的循环对称复高斯(Circularly Symmetric Complex Gauss, CSCG)分布，即满足。故式(1)变化为

此时，整个系统的联合接收信号可以表示为

根据式(4)，式(3)可以改写为

3 稳健的干扰对齐算法

3.1 算法描述

为了让系统总的自由度达到最大，此处仍将每个用户的自由度设定为。在上述的系统模型下，对于非理想的干扰安排，为了求取最优的干扰安排矩阵和，具体实现步骤为：

对于接收端而言，本文通过最小化发送端数据流和接收端数据流的差异来求取。根据最小均方误差(Minimum Mean Square Error, MMSE)准则，得到如下优化问题：

利用矩阵运算得到：

对于式(11)的优化问题，发送端的最优预编码矩阵可由式(12)得到。

对于矩阵而言，求其Frobenius范数就是求矩阵协方差的迹，故式(12)可以变为

由矩阵理论可知，式(13)可转化为求内项的d个最小特征值对应的特征向量问题：

(4)重复步骤(2)和步骤(3)，直到收敛。

3.2 收敛性分析

接收端经过干扰抑制处理后，接收信号中仍然存在的干扰功率，称之为干扰泄露。发送端泄露到非目标接收端的总功率为

其中，接收端的干扰协方差矩阵为

在本文第5.5节给出了系统容量与迭代次数关系的仿真图，进一步验证了算法的收敛性和可行性。

4 自由度及频谱效率分析

4.1 理想CSI情况下等效联合信道下的自由度保持不变

在理想CSI的情况下，相对于每个接收端，要使接收端收到的干扰对齐到干扰抑制矩阵的零空间上，发送端的预编码矩阵应满足的约束为

若要让系统的总自由度达到最大值min(r,t)/2，式(17)变化为

根据矩阵理论可知，对于维数匹配的矩阵，有

所以，QR分解并不影响干扰对齐的约束条件式(17)及式(18)的满足，故不影响其总自由度。

4.2 具有误差CSI情况下的自由度分析

在理想CSI的情况下，接收端只需对来自其他发送端的干扰信号进行简单的迫零处理，达到消除已在发送端被对齐的干扰的目的，所以在理想CSI的情况下，干扰对齐的目标为

然而，在实际通信系统中，由于信道估计误差等原因，CSI往往是有误差的，此时干扰对齐的目标为

4.3具有误差CSI情况下的频谱效率分析

在误差CSI的情况下，必须应用真实含有误差的联合信道矩阵求取信道容量。通过本文第2节系统模型与QR分解的分析可以知道，等效的真实信道联合矩阵为

所以，信道存在误差条件下系统的和速率为

5 仿真结果及性能分析

利用Matlab进行频谱效率、能量效率和误比特率等性能仿真。考虑基于3个相邻小区系统环境，其中每个小区存在1个边缘用户，每个基站的发送天线数t为2，每个用户的接收天线数r也为2，并且每个用户对应的自由度均为1，即1=2=3=1，所以系统的总自由度为3。假设所有收发天线间的信道均为平坦瑞利衰落信道，信道矩阵元素独立同分布，均满足均值为0和方差为1的复高斯随机分布。在比较具有信道误差时，信道误差的方差取值为0.05。

接下来，将对本文算法与稳健对称MMSE算法(Robust MMSE IA)[6]、稳健最小干扰泄露算法(Robust Min-IL IA)[11]、自适应最小化BER算法(Robust Adaptive IA)[12]、最大干扰比算法(MAX- SINR IA)[15]等进行仿真比较。

5.1理想CSI下的平均频谱效率仿真

在理想CSI时，对比几种算法的信道容量，如图1所示。本文算法一方面减少了干扰，另一方面又考虑了如何提高信号本身的传输质量，所以性能较好。而稳健最小干扰泄露算法(Robust Min-IL IA)[11]主要考虑的是减少干扰泄露，并没有考虑信号本身的传输质量，所以信道容量没有本文算法好。而稳健对称MMSE算法(Robust MMSE IA)[6]和最大信干噪比算法(MAX-SINR IA)[15]，充分考虑直接信道和干扰信道的影响，以最大化信干噪比为目标，而本文算法由于做了QR分解，降低了算法对干扰的灵敏度，所以最大信干噪比算法的信道容量大于最小干扰泄露算法，而小于本文算法。而自适应最小化BER算法(Robust Adaptive IA)[12]改进了最小干扰泄露和最大信干噪比算法的性能，所以性能好于后两者，然而它并不能降低干扰对齐对干扰的灵敏度，所以相对于本文算法而言性能要差一些。

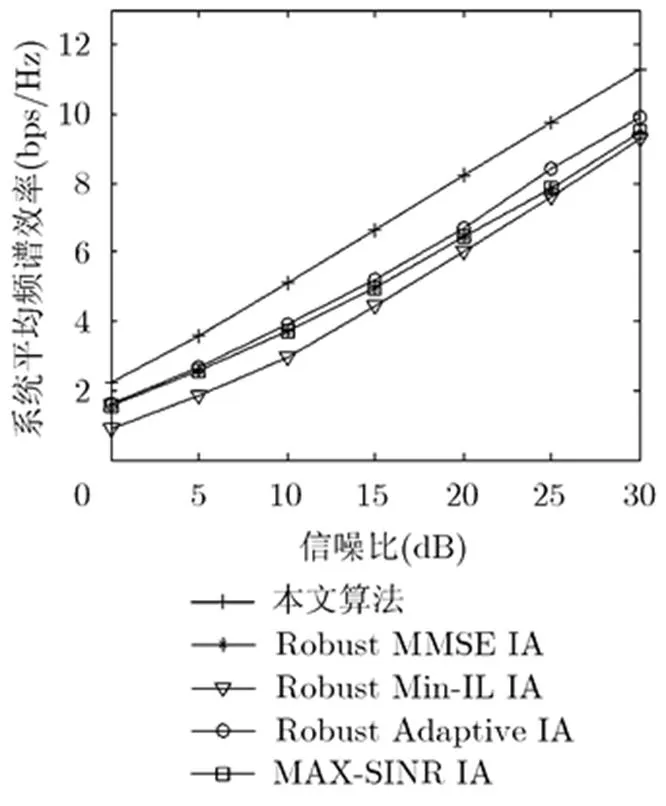
图1 理想CSI下算法平均频谱效率对比

5.2具有信道误差时的平均频谱效率

在误差CSI时，对比几种算法的信道容量，如图2所示。因为本文算法对联合信道矩阵进行了QR分解同时压缩了干扰项和误差项的空间维度，且同时提高信号的信干噪比，增强了系统的稳健性。文献[11]提出的Robust Min-IL IA算法，仅仅最小化具有误差的干扰项和直接信道的误差项所占用的空间维度，并没有考虑如何提高信号本身的传输质量。而文献[6]提出的稳健对称MMSE算法(Robust MMSE IA)，相对于Robust Min-IL IA算法而言，最小化干扰项和误差项所占用的空间维度，同时最大化信号本身的传输质量，所以性能好于Robust Min-IL IA算法；而本文算法进一步消除了一半具有误差的干扰信道，所以本文算法性能较Robust MMSE IA好。自适应最小化BER算法(Robust Adaptive IA)[12]通过自适应算法，最小化所有干扰项和误差项所占用的空间维度，同时最大化信号本身，所以性能好于文献[6]和文献[11]的算法，然而它并不能降低干扰对齐对干扰的灵敏度，所以相对于本文算法而言性能要差一些。从图2中也可以看出，对于所有的IA算法而言，由于信道误差项的存在，使信号泄露到干扰空间成为限制信道容量的主要因素，所以信道容量不能进一步提高，存在容量极限。

图2 具有信道误差时算法平均频谱效率对比

5.3 具有信道误差时的平均能量效率仿真

定义平均能量效率为单位带宽内单位能量能够传输的信息比特数，即，其单位为，其中是用户的发送功率。从图3，可以看出，在误差CSI条件下，采用本文算法，使系统的平均能量效率较Robust Min-IL IA算法[11]、Robust MMSE IA算法[6]和Robust Adaptive IA算法[12]的平均能量效率有一定的提高。

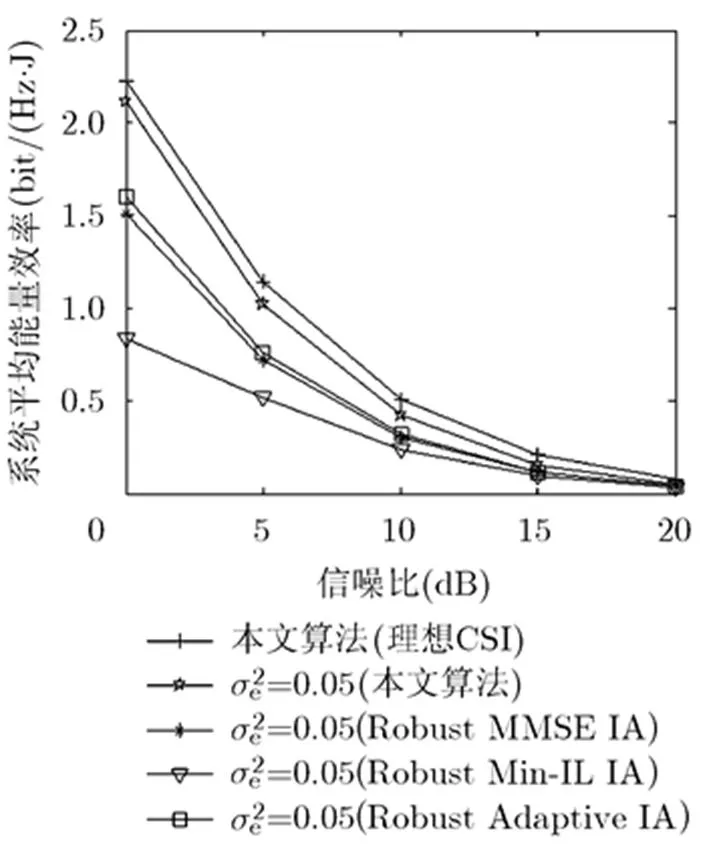
图3 具有信道误差时算法能量效率

5.4具有信道误差时的误比特率(BER)仿真

在误差CSI时，图4仿真了几种算法的BER性能。图中显示的是使用QPSK调制时，系统的误比特率随发送端信噪比的变化。从图中可以看出，采用本文算法之后，相对于Robust Min-IL IA算法和Robust MMSE IA算法而言，系统的BER得到了改善。文献[12]提出的自适应算法，以最小化BER为目标自适应的选择比特加载的MIN-IL, Max-SINR, SVD算法，由于本文算法通过信道联合处理，减少了一半的干扰，在等效后的联合信道中，通过最小化发送端泄漏到非目标接收端的信号功率来设计等效预编码矩阵，且应用MMSE准则来设计干扰抑制矩阵，进一步提高了性能，所以较文献[11]和文献[6]的BER性能好。

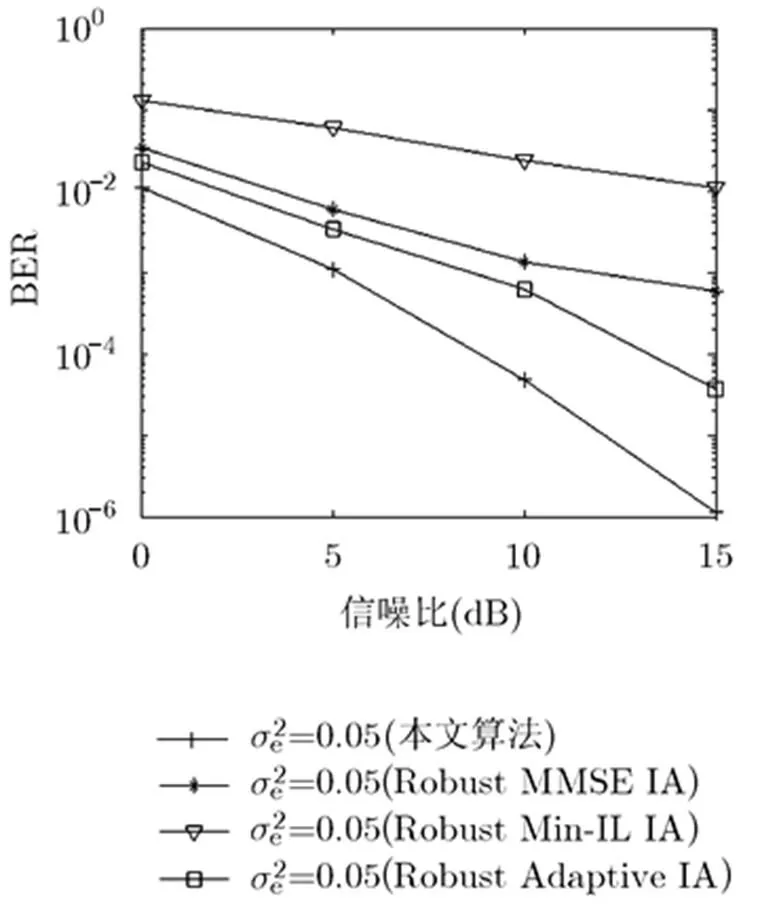
图4 具有信道误差时算法的BER

5.5具有信道误差时的迭代次数与平均频谱效率的仿真

图5(a)和图5(b)分别为几种算法在每个用户发射功率为5 dB, 10 dB时，平均频谱效率与迭代次数关系的仿真图。从图中可以看出，在误差CSI时，本文算法，Robust Adaptive IA[12]和Robust MMSE IA[6]算法的平均频谱效率大概在迭代12次左右趋于饱和，而Robust Min-IL IA[11]的收敛速度要慢一些，大致在20次左右的迭代才能达到饱和。从图中也可以看出，本文算法在迭代次数没有增加的情况下，提高了系统的性能，进一步证实了本文算法的收敛性和可行性。

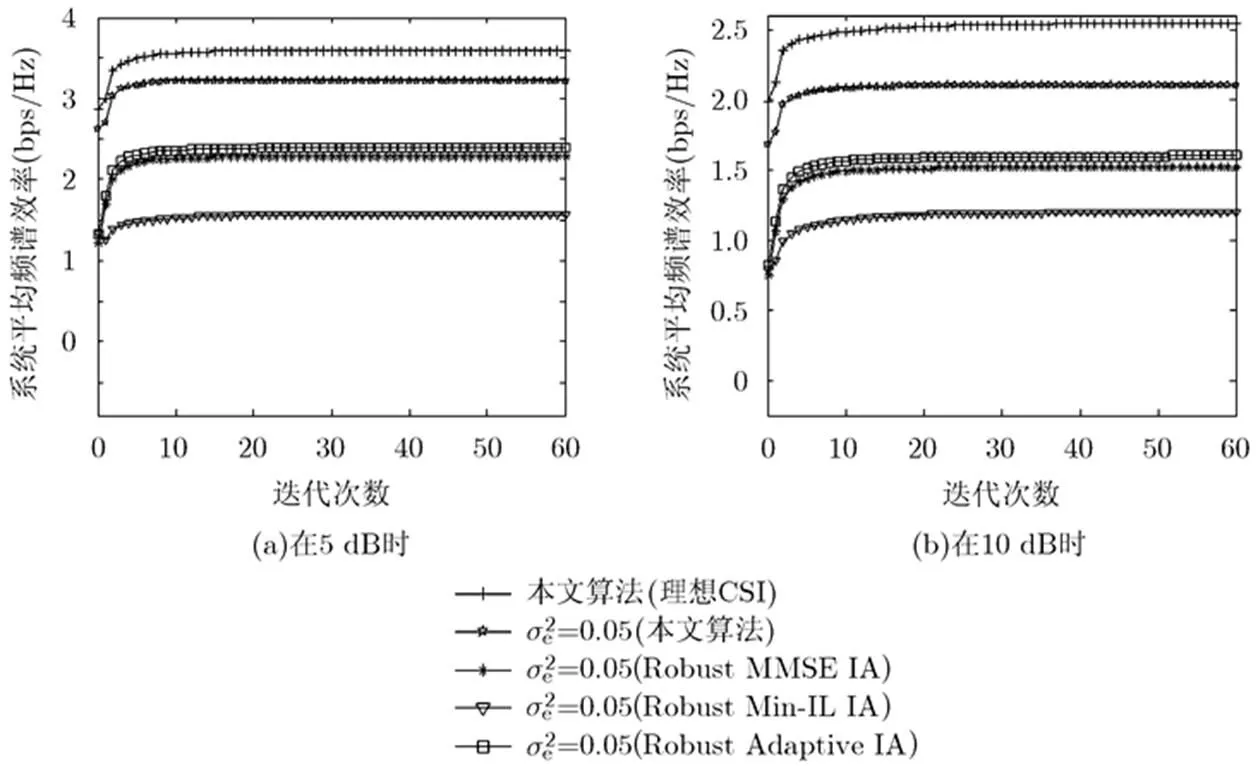
图5 平均频谱效率与迭代次数的关系

6 结束语

本文研究了实际MIMO通信系统中，由于信道在测量或反馈中存在误差使得性能恶化的情况。为此，本文提出一种基于联合信道QR分解的稳健干扰对齐算法，在设计中最小化信道误差项和干扰项的影响。由仿真结果可知，本文算法提高了系统的系统容量和频谱效率，改善了BER性能，有效地降低了信道误差对系统性能的影响，增强了系统的稳健性。

参考文献

[1] Cadambe V R and Jafar S A. Interference alignment and the degree of freedom for the-user interference channel[J]., 2008, 54(8): 3425-3441.

[2] Maddah-Ali M, Motahari A, and Khandani A. Communication over MIMO X channels: interference alignment, decomposition, and performance analysis[J].2008, 54(8): 3457-3470.

[3] Xu Sheng-feng, Zhu Gang, Sun Qian,.. Joint interference alignment and power allocation in MIMO interference network[C]. Proceedings of the 9th International on Wireless Communications and Mobile Computing Conference (IWCMC), Sardinia, Italy, 2013: 1258-1262.

[4] Omar El Ayach, Steven W, and Robert W. The practical challenges of interference alignment[J]., 2013, 20(1): 35-42.

[5] Dong An-ming, Zhang Hai-xia, and Yuan Dong-feng. Achievable rate improvement through channel prediction for interference alignment[C]. Proceedings of the 19th Asia-Pacific Conference on Communications (APCC), Bali,Indonesia, 2013: 293-298.

[6] Schmidt D, Shi C, Berry R,.. Minimum mean squared error interference alignment[C]. Proceedings of the IEEE43th Asilomar Conference on Signals, Systems and Computers, Asilomar, America, 2009: 1106-1110.

[7] Shen H, Li B, Tao M,.. MSE-based transceiver designs for the MIMO interference channel[J]., 2010, 9(11): 3480-3489.

[8] Tresch R and Guillaud M. Cellular interference alignment with imperfect channel knowledge[C]. Proceedings of the IEEE International Conference onCommunications Workshops, Dresden, Germany, 2009: 1-5.

[9] Farhadi H, Zaidi A A, Fischione C,Distributed interference alignment and power control for wireless MIMO interference networks with noisy channel state information [C]. 2013 First International Black Sea Conference on Communications and Networking, Batumi, Georgia, 2013: 23-27.

[10] Huang Huang, Lau V K N, Du Ying-gang,Robust lattice alignment for-user MIMO interference channels with imperfect channel knowledge[J]., 2011, 59(7): 3315-3325.

[11] 谢显中，邵奇，周志栋，等. 非理想信道状态信息下的稳健干扰安排设计[J]. 北京邮电大学学报, 2012, 35(3): 6-10.

Xie Xian-zhong, Shao Qi, Zhou Zhi-dong,A robust interference alignment scheme with imperfect CSI used in multi-cell system[J]., 2012, 35(3): 6-10.

[12] Xie Bai-le, Li Yang, Minn Hlaing,Adaptive interference alignment with CSI uncertainty[J].,2013, 61(2): 792-801.

[13] Mahmoud A, El-Khamy M, and Elsayed K. Interference alignment performance on MIMO X channels with imperfect channel knowledge[C]. Proceedings of the IEEE 13th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC),Istanbul, Turkey, 2012: 239-243.

[14] 谢显中, 徐冰, 雷维嘉, 等. 三小区环境中基于三角分解的低复杂度干扰对齐算法[J]. 电子与信息学报, 2013, 35(5): 1031-1036.

Xie Xian-zhong, Xu Bing, Lei Wei-jia,.. Interference alignment algorithm based on orthogonal-triangular decomposition for edge users in 3-cell MIMO cellular networks[J].&, 2013, 35(5): 1031-1036.

[15] Gomadam K, Cadambe V R, and Jafar S A. Approaching the capacity of wireless networks through distributed interference alignment[C]. Proceedings of the IEEE Global Telecommunications Conference (GLOBLECOM), New Orleans, LA, USA, 2008: 1-6.

Robust Interference Alignment Algorithm Based on QR Decomposition

Xie Xian-zhong Zhang Sen-lin Xiao Zheng-ying

(,,400065,)

Most interference alignment algorithms assume that the senders know perfect Channel State Information (CSI), but in practical communication systems, due to the channel estimation error, the delayed feedback and so on, the CSI often exists the error. Therefore, a robust interference alignment algorithm is presented based on the QR decomposition. Firstly, the QR is used to preprocess the jointly received signal with the of error for eliminating half of the interference terms. Then this paper minimizes the interference power from the sender to the other receivers to design the pre-coding matrix, and utilizes Minimum Mean Square Error (MMSE) criterion to design the interference suppression matrix. Finally, under the conditions of perfect CSI and error CSI, the simulation results verify that the proposed algorithm improves effectively the performance of the system.

Wireless communication; Robust interference alignment; Channel estimation error; QR decomposition; Performance of system

TN929.53

A

1009-5896(2015)08-1957-07

10.11999/JEIT141585

谢显中 xiexzh@cqupt.edu.cn

2014-12-11收到，2015-04-20改回，2015-06-08网络优先出版

国家自然科学基金(61271259, 61301123)，重庆市自然科学基金(CTSC2011jjA40006)，重庆市教委科学技术研究项目(KJ120501, KJ130536)，长江学者和创新团队发展计划(IRT1299)和重庆市科委重点实验室专项经费(CSTC)资助课题

谢显中： 男，1966年生，博士，教授，研究方向为认知无线电、干扰对齐、预编码技术、通信信号处理等.

张森林： 男，1987年生，硕士生，研究方向为干扰对齐技术.

肖正瑛： 男，1988年生，硕士生，研究方向为认知无线电技术.