基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计

梁 浩 崔 琛 代 林 余 剑



基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计

梁 浩*崔 琛 代 林 余 剑

(合肥电子工程学院401室 合肥 230037)

该文针对L型阵列MIMO雷达的2维角度估计问题，基于ESPRIT算法提出两种降维DOA估计方法。首先通过降维矩阵的设计及回波数据的降维变换，将高维回波数据转换至低维信号空间；然后分别基于特征分解和传播算子获得信号子空间的估计，最后利用ESPRIT算法实现2维空间角参量的联合估计及参数的自动配对。算法不牺牲阵列孔径，最大程度地降低了回波数据的维数，具有更低的运算复杂度。仿真结果验证了该文理论分析的正确性和算法的有效性。

MIMO雷达；L型阵列；降维ESPRIT；低复杂度

1 引言

以多输入多输出(MIMO)技术为基础体制的MIMO雷达系统[1,2]，在目标检测、参数估计、杂波抑制等方面具有诸多优势，成为近年来学术界研究的热点。L型阵列结构简单、阵列冗余度较小，能够实现空域目标2维角度定位，具有优于其他交叉阵列结构的DOA(Direction Of Arrival)估计性能[3]；此外，当收、发阵列采用L型结构时，意味着目标参数维度的扩展，对目标的描述也就更准确，因此深入研究L型阵列MIMO雷达的参数估计问题具有重要意义和实用价值。

目前对MIMO雷达参数估计的研究大多集中在单基地MIMO雷达1维角度估计以及双基地的2维角度估计，鉴于线性配置下的单/双基地MIMO雷达与线阵/平面阵的等效相似性，传统阵列信号处理中的超分辨参数估计算法ML (Maximum Likelihood), ESPRIT (Estimation of Signal Parameters by Rotational Invariance Techniques)以及MUSIC (MUltiple SIgnal Classification)等被广泛应用于MIMO雷达的目标参数估计中，并取得了一系列成果；而关于L型阵列配置下的MIMO雷达参数估计问题研究相对较少，仅有的研究：文献[11]基于DOA矩阵思想，通过划分Ｌ型阵列MIMO雷达所虚拟的平面阵，实现了目标2维角度的估计，并进一步提出联合对角化DOA矩阵方法解决了角度兼并问题；但该模型采用收发阵列垂直分置的L型配置，因此算法并不适用于收发均为L型配置的共置MIMO雷达。文献[12]建立了L型阵列配置的单基地MIMO雷达系统，并基于Capon波束形成器的MIMO-Capon算法实现了目标方位角和俯仰角的2维估计；理论分析和仿真结果表明，L型阵列配置的单基地MIMO雷达在实际阵元数相同的条件下，能够产生更多的虚拟阵元，提高目标的分辨能力，但算法需要2维的谱搜索；文献[13]针对文献[12]算法计算复杂度较高的问题，提出一种基于MUSIC算法的L型阵列多输入多输出雷达降维DOA估计算法。算法根据L型阵列导向矢量的结构，通过构造降维矩阵及降维预处理后，利用二次优化方法将2维DOA估计分解为两个1维DOA估计，一定程度上降低了运算复杂度，但存在以下问题：(1)降维矩阵并没有最大程度地降低回波数据的维数，没有去除所有重复的虚拟阵元，回波数据中仍存在冗余；(2)在利用二次优化进行降维求解过程中，对方向向量中各元素的约束较弱[14]，造成估计精度较差，同时协方差矩阵的构建和特征分解以及两次1维谱搜索仍存在较高的运算量。

本文针对文献[13]算法存在的不足，基于ESPRIT算法提出两种L型阵列MIMO雷达降维DOA估计算法。通过降维矩阵的设计及回波数据的降维变换，将高维回波数据转换至低维信号空间，然后分别基于特征分解和传播算子实现对信号子空间的估计，并通过对2维空间角旋转不变因子的提取，利用ESPRIT算法实现了参数的联合估计；算法不牺牲阵列孔径，且最大程度地降低了回波数据的维数，具有更低的运算复杂度；仿真结果验证了本文理论分析的正确性和算法的有效性。

2 问题建模

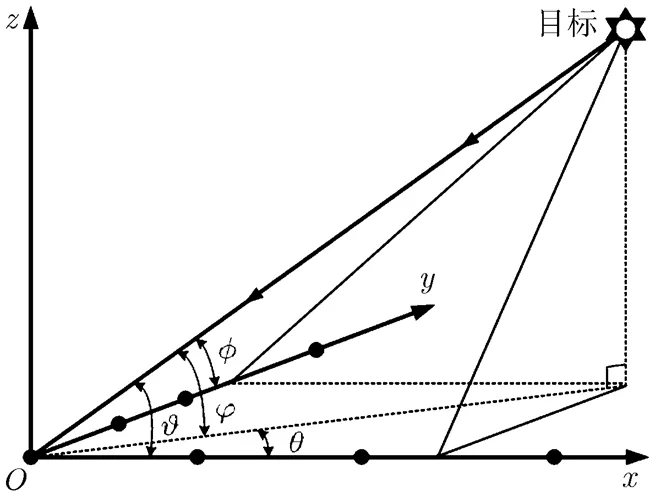
图1 L型阵列MIMO雷达结构及角度配置关系

3 算法分析

3.1降维预处理

由信号模型可得：

则存在线性变换

式(12)证明略。从式(11)和式(12)可得，降维后的回波数据可以等效为长度为的加权平面阵的回波信号，权值为对角阵的对角元素。显然，由可知，本文降维处理最大程度地降低了回波数据的维数，去除了原始回波数据中所有重复量，达到了降维的目的。

3.2信号子空间的获取

3.2.1基于特征分解的信号子空间估计 计算降维后的回波协方差矩阵，并对其进行特征分解：

3.2.2基于传播算子的信号子空间快速估计 上节分析能够很好地实现信号子空间的估计，但需要信号协方差的计算以及相应的特征分解，当快拍数较大时，其运算复杂度较高；为了避免协方差矩阵的估计及其特征分解，本节基于传播算子进行信号子空间的估计。由上节分析可知，降维后回波数据可以等效为长度为的加权平面阵的回波信号，权值为对角阵的对角元素，为了处理方便，首先对降维后的回波数据进行权值归一化操作，即；其中为噪声项。假设雷达阵列无空间模糊，即为列满秩矩阵，则在中有行是线性独立的，将导向矩阵分块为，式中,分别为维和维矩阵，则存在线性变换矩阵(即传播算子)使得；同理在得到后，进行分块处理，令，其中,分别对应的前行和后行元素。则无噪的情况下有，考虑到实际中噪声对回波数据的影响，矩阵可由代价函数估计得到，表示Frobenius范数，则矩阵的最小二乘解为。令,为维单位阵，存在

3.3基于ESPRIT的2维旋转因子提取

3.4 算法性能分析

3.4.1等效虚拟分析及移不变子阵划分 L型阵列MIMO雷达虚拟扩展示意如图2所示。本文通过降维矩阵的设计，将维的回波信号降至维，有效地去除了所有的重复阵元，而文献[13]RD_MUSIC仅仅是将维的雷达回波信号降至维，降维后仍存在个重复阵元；显然与文献[13]RD_MUSIC相比，本文降维预处理将回波数维数降到了最低，最大限度地降低了处理数据的维度和数据量。同时本文2维旋转不变因子提取方法对应的等效平移子阵可用图2来进行直观解释，利用子阵1与子阵2的平移不变性即可获得对的估计；利用子阵3与子阵4的平移不变性即可获得对的估计，从而实现对空间角的估计。同时由图2可以看出，虚拟后的MIMO雷达阵列在整个平面上关于对称，即，这就为基于同一信号子空间，来分别获取2维空间角的旋转不变因子提供了条件；此外，本文2维旋转不变因子提取方法利用到了所有的有效虚拟阵元，在实现参数自动配对的同时，不损失雷达孔径，提高了整个阵列的阵元利用率。

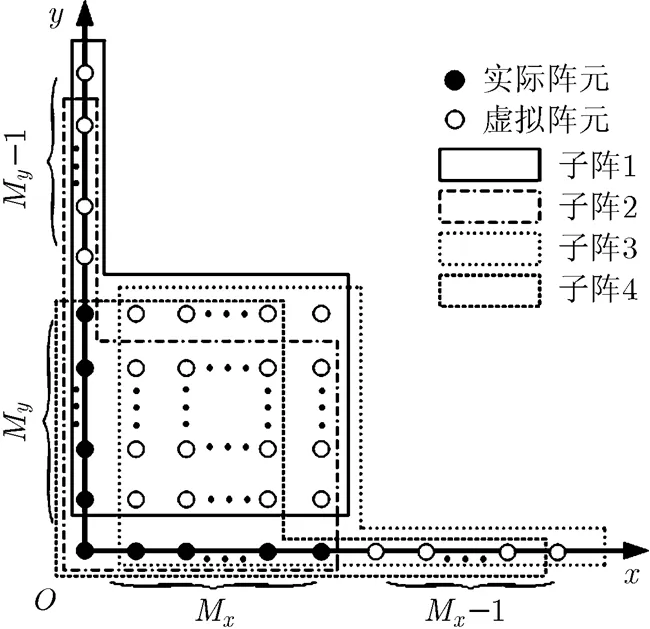
图2 虚拟扩展及移不变子阵划分示意图

3.4.2运算复杂度及最大可分辨目标数 将本文降维预处理后基于特征分解获得2维角度估计的算法称为RD_ESPRIT算法；降维预处理后基于传播算子获得2维角度估计的算法称为RD_PM_ ESPRIT算法。由前文分析可得，本文算法的数据维数为，则运算量为。对应的本文RD_PM_ESPRIT算法的运算量为：。文献[13]2D_MUSIC算法的数据维数为，算法总的计算量。文献[13]RD_MUSIC算法处理的数据维数为，算法总的计算量。为谱搜索的栅格数，显然，同时快拍数以及栅格数要远大于，易得。

此外，本文无论是RD_ESPRIT算法还是RD_ PM_ESPRIT算法，在2维空间角求解过程中，为了使分块矩阵满足列满秩条件，即；因此所提两种算法的最大可分辨目标数均为。

4 仿真实验与分析

实验1 算法的有效性验证

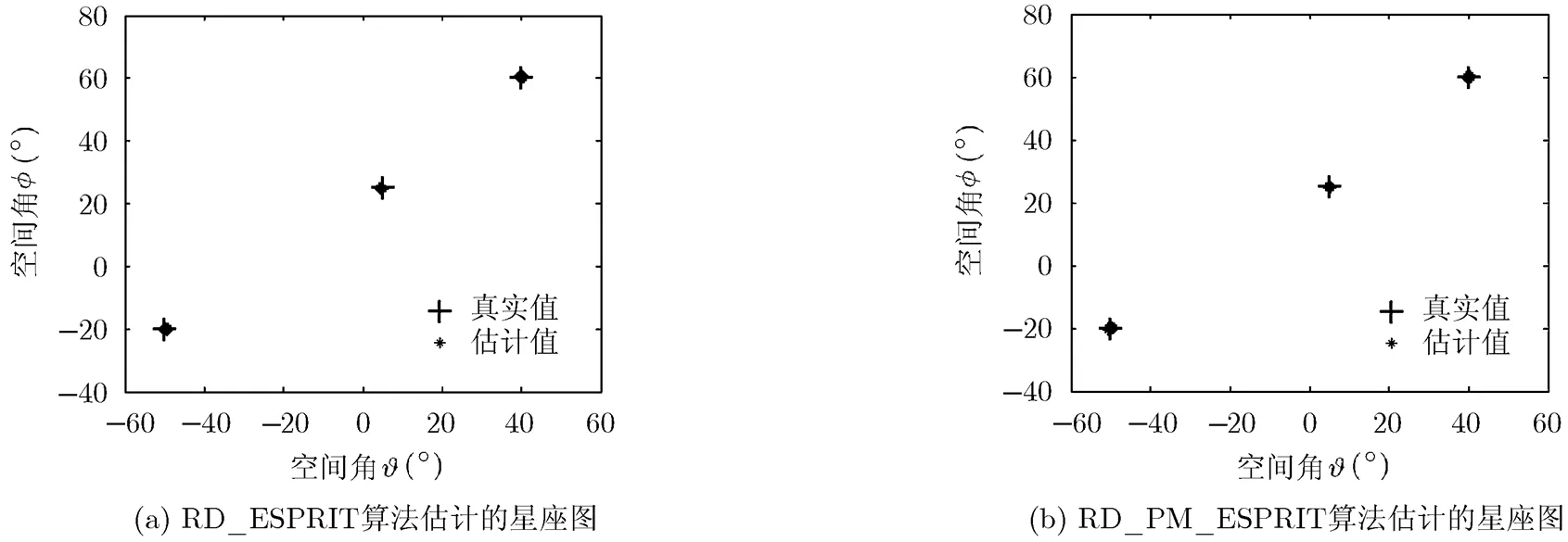
图3 星座图估计结果

实验2 算法的估计性能比较

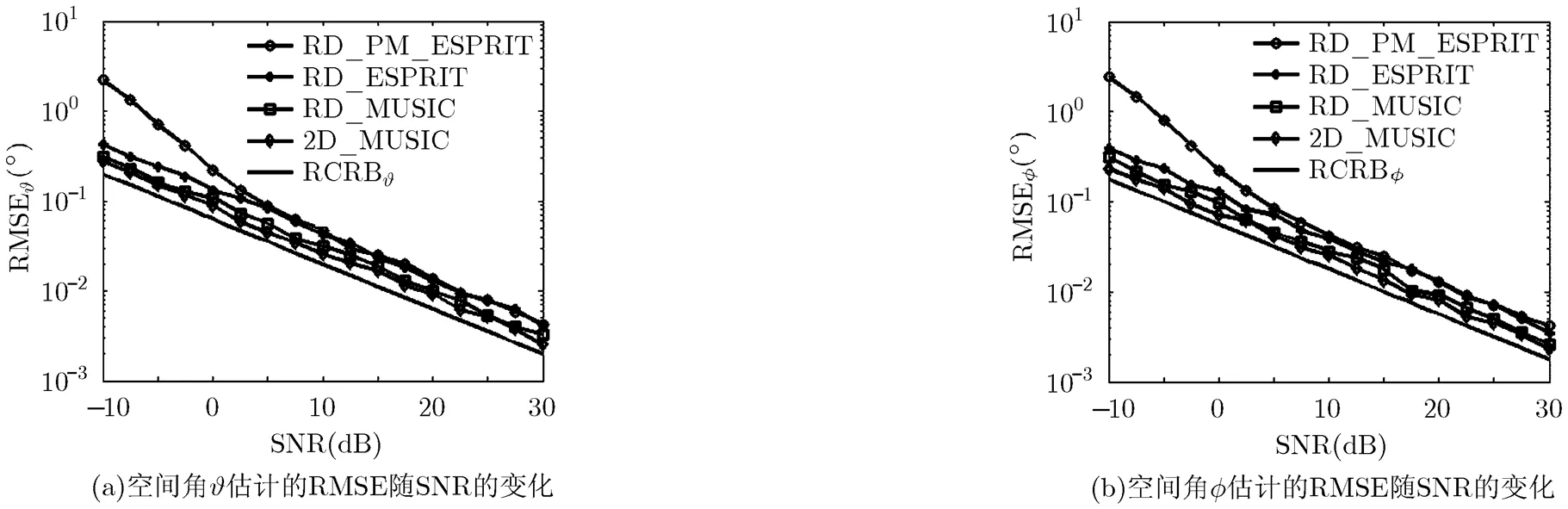
图4 空间角估计结果

实验3 算法的性能与参数之间的关系

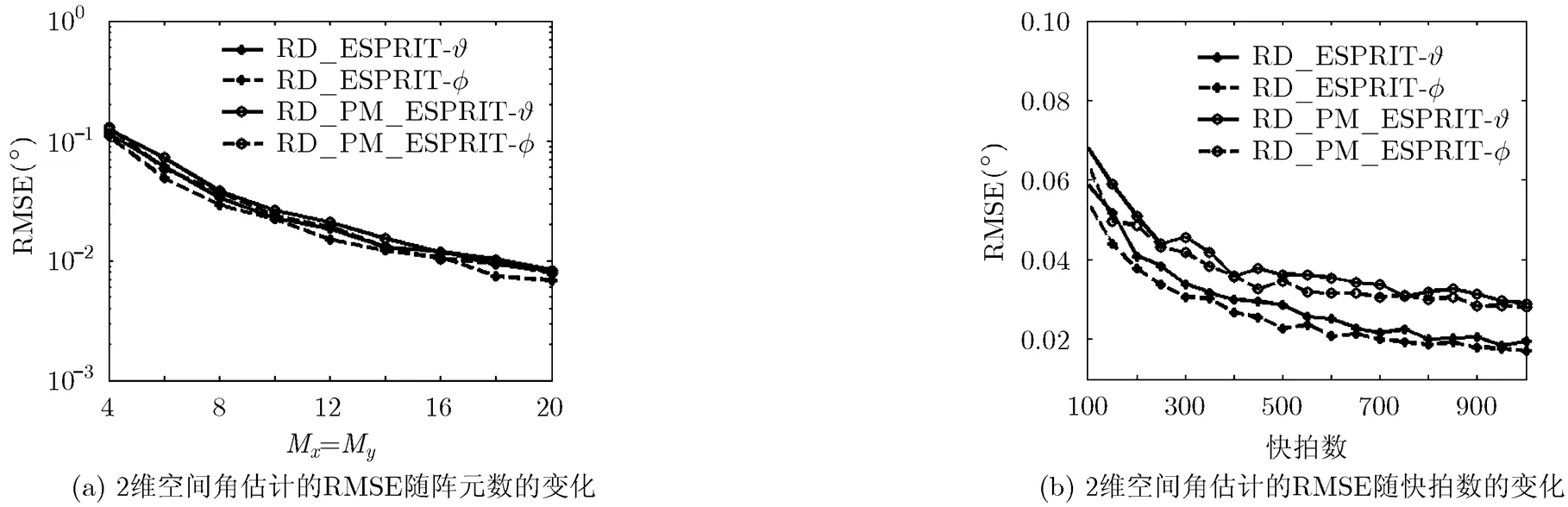
图5 空间角估计结果与阵元数快拍数的关系

5 结论

针对L型阵列MIMO雷达的2维角度估计问题，基于ESPRIT算法提出两种L型阵列MIMO雷达降维DOA估计算法，即基于特征分解的降维DOA估计算法(RD_ESPRIT)和基于传播算子的降维DOA估计算法(RD_PM_ESPRIT)。理论分析和实验仿真表明：(1)所提两种算法均通过降维预处理，将高维回波数据转换至低维信号空间，有效降低了数据处理的维数，降低了所需处理的回波的数据量；(2)所提两种算法分别基于特征分解与传播算子实现信号子空间的估计，实现了2维空间角旋转不变因子的提取，有效地估计出目标2维空间角度的同时，实现了参数的自动配对；(3)与已有文献算法比，两种算法在估计性能接近的条件下，最大程度地降低了回波数据的维数，同时利用ESPRIT算法大大降低了传统算法由于谱峰搜索所带来的巨大运算复杂度，提高了算法应用的实时性；(4)两种算法中，RD_PM_ESPRIT算法进一步避免了协方差矩阵的构造与特征分解，具有更低的运算复杂度，在低信噪比时，RD_ESPRIT算法的参数估计性能要优于RD_PM_ESPRIT算法，在高信噪比时，两者的估计性能趋于一致，因此在实际工程中可以在估计精度与运算复杂度之间灵活选用合适的算法。

参考文献

[1] Chen H W, Li X, Jiang W D,MIMO radar sensitivity analysis of antenna position for direction finding[J]., 2012, 60(10): 5201-5216.

[2] Huleihel W, Tabrikian J, and Shavit R. Optimal adaptive waveform design for cognitive MIMO radar[J]., 2013, 61(20): 5075-5089.

[3] Cheng Q and Hua Y. Further study of the pencil-MUSIC algorithm[J]., 1996, 32(1): 284-299.

[4] Tang B, Tang J, Zhang Y,.. Maximum likelihood estimation of DOD and DOA for bistatic MIMO radar[J]., 2013, 93(5): 1349-1357.

[5] Arash K, Aboulnasr H, Sergiy A V,.. Efficient transmit beamspace design for search-free based DOA estimation in MIMO radar[J]., 2014, 62(6): 1490-1500.

[6] Bencheikh M L and Wang Y. Joint DOD-DOA estimation using combined ESPRIT-MUSIC approach in MIMO radar [J]., 2010, 46(15): 2686-2691.

[7] Li C C, Liao G S, Zhu S,.. An ESPRIT-like algorithm for coherent DOA estimation based on data matrix decomposition in MIMO radar[J]., 2011, 91(8): 1803-1811.

[8] Zheng G M, Chen B X, and Yang M L. Unitary ESPRIT algorithm for bistatic MIMO radar[J]., 2012, 48(3): 179-181.

[9] Li J F and Zhang X F. A method for joint angle and array gain-phase error estimation in bistatic multiple input multiple output nonlinear arrays[J]., 2014, 8(2): 131-137.

[10] Jiang H, Zhang Y, Li J,. A PARAFAC-based algorithm for multi-dimensional parameter estimation in polarimetric bistatic MIMO radar[J]., 2013, 2013(1): 1-14.

[11] 符渭波, 赵永波, 苏涛, 等. 基于L型阵列MIMO雷达的DOA矩阵方法[J]. 系统工程与电子技术, 2011, 33(11): 2398-2403.

Fu W B, Zhao Y B, Su T,..DOA matrix method based on MIMO radar with L-shape arrays[J]., 2011, 33(11): 2398-2403.

[12] 谢荣, 刘铮, 等. 基于L型阵列MIMO雷达的多目标分辨和定位[J]. 系统工程与电子技术, 2010, 32(1): 49-52.

Xie R, Liu Z,.. Multi-target identification and localization in MIMO radar with L-shape arrays[J]., 2010, 32(1): 49-52.

[13] 王伟, 王晓萌, 李欣, 等. 基于MUSIC算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2014, 36(8): 1954-1959.

Wang W, Wang X M, Li X,.. Reduced-dimensional DOA estimation based on MUSIC algorithm in MIMO radar with L-shaped array[J].&, 2014, 36(8): 1954-1959.

[14] 蔡晶晶, 鲍丹, 李鹏, 等. 强约束优化降维MUSIC二维DOA估计[J]. 电子与信息学报, 2014, 36(5): 1113-1118.

Cai J J, Bao D, Li P,.. Two-dimensional DOA estimation using reduced-dimensional MUSIC algorithm with strong- constraint optimization[J].&, 2014, 36(5): 1113-1118.

[15] Zhang X and Xu D. Low-complexity ESPRIT-based DOA estimation for colocated MIMO radar using reduced- dimension transformation[J]., 2011, 17(47): 283-284.

[16] 郑志东, 张剑云, 康凯, 等. 互耦条件下双基地MIMO雷达的收发角度估计[J]. 中国科学: 信息科学, 2013, 43(6): 784-797.

Zheng Z D, Zhang J Y, Kang K,.. Joint DOD and DOA estimation for bistatic MIMO radar in the presence of mutual coupling[J]., 2013, 43(6): 784-797.

[17] 郑志东, 张剑云, 屈金佑, 等. 新的双基地MIMO雷达角度估计方法[J]. 通信学报, 2012, 33(12): 123-132.

Zheng Z D, Zhang J Y, Qu J Y,.. Novel method for angle estimating of bistatic MIMO radar[J]., 2012, 33(12): 123-132.

Reduced-dimensional DOA Estimation Based on ESPRIT Algorithm in MIMO Radar with L-shaped Array

Liang Hao Cui Chen Dai Lin Yu Jian

(401,,230037,)

In order to solve the issue of two dimensional angles estimation for MIMO radar with L-shaped array, two novel reduced-dimensional Direction Of Arrival (DOA) estimation methods using ESPRIT algorithm are proposed. Firstly, through the reduced-dimensional matrix design and reduced-dimensional transformation, the high dimensional received data can be transformed into a lower dimensional signal space. Then, the signal space can be achieved via the eigen-value decomposition and propagator operator method respectively, and two dimensional spatial angle parameters can be joint estimated using ESPRIT algorithm with automatic pairing. The proposed two methods remove data redundancy of high dimensional received data at the greatest degreewithout costing the aperture of array and have lower computation complexity. Simulation results verify the correctness of theoretical analysis and the effectiveness of proposed algorithm.

MIMO radar; L-shaped array; Reduced-dimensional ESPRIT; Low complexity

TN958

A

1009-5896(2015)08-1828-08

10.11999/JEIT141295

梁浩 lhmailhappy@163.com

2014-10-09收到，2015-05-07改回，2015-06-08网络优先出版

国家自然科学基金(60702015)和电子工程学院院控科研基金(KY13A206)资助课题

梁 浩： 男，1987年生，博士生，研究方向为阵列信号处理以及MIMO雷达信号处理.

崔 琛： 男，1962年生，教授，博士生导师，研究方向为雷达信号处理以及雷达对抗技术.

代 林： 男，1986年生，博士生，研究方向为压缩感知理论的研究与应用.

余 剑： 男，1980年生，讲师，硕士，研究方向为雷达信号处理以及雷达对抗技术.