分布式雷达相参发射原理与性能分析

臧会凯 雷 欢 但晓东 周生华 刘宏伟



分布式雷达相参发射原理与性能分析

臧会凯*雷 欢 但晓东 周生华 刘宏伟

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

通过调整空间距离较远的雷达发射天线的发射时间和初始相位可控制电磁波能量在空间的分布来增强感兴趣空间区域的信号能量。该文分析分布式雷达相参发射的原理，给出形成干涉峰点的条件，定义空间干涉能量分布函数来反映发射信号能量较平均能量的增益，其最大值为发射天线个数。在远场和近场条件下分析信号空间能量分布的特点，表明它在远场近天线距离呈条纹状，在近场远天线距离呈类晶体结构或独峰结构。为了让目标在干涉峰点内部，分布式相参发射在低频率、小目标的跟踪状态更有效。

分布式雷达；分布式相参发射；空间干涉能量分布函数；干涉峰点

1 引言

2 分布式雷达相参发射原理

2.1 分布式相参发射工作方式

根据假设，各雷达站发射信号的包络信号是正实信号，为了满足条件(2)，令第个雷达站与标定点构成向量，在该点的波数方向为，根据式(4)，则应存在一组整数，满足

由式(7)可知，若实际中能精确地满足式(5)，则只需要使各个雷达站发射信号的初始相位相同即可，即。但这需要精确控制信号的发射时间，在实际中可能很难做到，有时也没有必要。根据式(6)，若发射信号的包络在工程上只能粗略对齐，即

2.2 空间干涉能量分布函数

雷达发射的信号为有限时宽的脉冲信号，因此，在一个快拍内，发射信号在空间形成干涉的时间和空间都是有限的；为了方便研究空间干涉能量的分布，这里先假设发射信号时宽无限并且在所有照射空间形成干涉，然后再限制干涉时间和空间的区域。根据式(9)，此时雷达干涉信号的时空表示可以写为

根据式(10)，定义空间干涉函数：

根据欧拉定理，式(11)可写为

为了方便，这里给出可能用到的符号定义如图1所示。

图1 矢量符号定义示意图

在实际中，雷达发射信号到达标定点时可能出现相位偏差，这种误差可能由雷达发射时间，初始相位或者雷达到标定点的信号通道的不理想造成，此时标定点的幅度可能达不到最大值。为了评估相位误差对标定点信号幅度的影响，假设第个雷达信号的相位误差为，所有雷达站误差相互统计独立，均在上服从均匀分布，此时信号时空表示可以写为

以上假设干涉区域分布于整个空间，但是在实际中，雷达发射信号通常是有限时宽信号，在空间形成有效干涉的时间和空间都是有限的，这可以结合具体参数算出，这里重点关注干涉场的问题，因此，不深入讨论干涉场的时间和空间边界问题。

3 干涉峰点产生条件与信噪比增益分析

3.1 空间干涉峰点产生的条件

根据式(14)，干涉能量增益分布函数满足

当且仅当

时取等号，此时形成驻波峰点；在驻波峰点，信号能量增益最大为，信号的干涉能量最大为。

在满足条件式(24)的前提下，形成干涉峰点的充分必要条件为

进而可知，满足式(25)的空间点应满足式(26)。

实际中，若到达标定点的信号幅度不同，则不能达到式(22)中的最大信号增益，为了计算信号幅度不同时的最大信号增益，考虑，可得不等式

可得

3.2 远场条件下的信号干涉

当雷达站之间的距离较近，而警戒区域的位置较远时，通常将标定点设置为某个方向无穷远的地方。在这种模式下，令第个天线到空间点构成的向量为，波数方向为，而阵列原点到空间点构成向量，基准原点与第个天线中心组成向量，则根据图1，它们满足关系为

在雷达远场满足条件为

此时，发射信号时空表示为

此时

4 仿真及分析

下面通过一些典型雷达配置条件下的干涉能量分布图从直观上观察发射信号的干涉能量分布问题。为了简便起见，以下总是假设发射信号同时到达标定点，发射信号到达所有空间区域时的能量相同，同时，发射信号没有时间和空间限制。在实际中雷达常发射脉冲信号，此时形成干涉的时间和空间是有限的。

4.1 雷达远场情形

假设雷达载频为10 GHz, 3个雷达站的坐标分别为(–10, 0) m, (0, 0) m和 (10, 0) m，标定点位置(0, 2000) km，此时在雷达站远场得到的干涉能量分布如图2所示。

图2 天线距离较远时远场的干涉能量分布图

由图2可知，此时干涉图样呈条纹形，但与半波间距相比，栅瓣的个数增多。在实际应用中，增加天线的距离会导致栅瓣的增加，在搜索状态下为了覆盖整个警戒空域，会大大增加系统的复杂度。

假设载频为10 GHz，3个雷达站的坐标分别为(–10, 10) m, (0, 0) m和 (10, 10) m，标定点位置(0, 2000) km，此时在雷达站远场得到的干涉能量分布如图3所示。

图3 天线距离较远且不在一条直线上时远场的干涉能量分布图

对比图2和图3可知，两图看不出明显的差异，因此，对于近天线距离远场且天线等间隔分布的情况，改变雷达站的位置对远场干涉能量分布的影响很小。

4.2雷达近场情形

考虑远天线距离近场情形，假设标定点在(0, 10) km，雷达的载频为1 GHz，3个雷达站的位置分别为(–5000, 1000) m, (0, 0) m和(5000, 1000) m，此时得到的干涉能量分布图如图4(a)所示，若3个雷达站坐标分别为(–1000, 100) m, (0, 0) m和(1000, 100) m，则得到的干涉能量分布图如图4(b)所示。

图4 远天线距离的空间干涉能量分布图

由图4可知，在远天线距离近场条件下，干涉能量分布图与雷达天线的间距具有重要的关系，雷达天线之间的距离越大，干涉峰点之间的距离就越小，干涉斑的尺寸也越小。

干涉能量分布图的干涉峰点间距与雷达波长关系较大，若雷达的载频为2.0 GHz, 3个雷达站位置分别为(–500, 500) m, (0, 0) m和(500, 500) m，标定点在(0, 1) km，此时得到的干涉能量分布如图5(a)所示。若雷达的载频改为0.5 GHz, 3个雷达站位置不变，此时得到的干涉能量分布如图5(b)所示。

图5 远场条件下雷达波长不同时的空间干涉能量分布图

由图5可知，雷达工作波长越长，干涉峰点之间的间距越大，干涉斑的尺寸也越大。在图5(a)中，雷达的工作波长为0.15 m，水平方向相邻干涉峰点间的距离约为0.216 m，垂直方向的距离约为0.6 m，斜对角方向的距离约为0.32 m。在图5(b)中，雷达的工作波长为0.6 m，水平方向相邻干涉峰点间的距离约为0.848 m，垂直方向的距离约为2 m，斜对角方向的距离约为1.1 m；干涉峰点区域呈椭圆形，如果以半功率点作为椭圆的边界，则椭圆的长轴和短轴的长度分别约为1.2 m和0.24 m。由图4和图5可知，此时干涉能量分布图的结构与晶体结构相似，任意两个干涉峰点组成的线段延长相同距离后必然是一个干涉峰点。

下面仿真当多个雷达站准确对准感兴趣点时空间信号干涉能量的分布状况。首先假设雷达载频为1 GHz，感兴趣点位于坐标原点，10个雷达站距离原点相同为1 km，从到等角度排列，此时得到的信号干涉能量分布函数如图6(a)所示。将图6(a)中的10个雷达站从到按随机的角度排列，此时得到的信号干涉能量分布函数如图6(b)所示。雷达站点数增加到30个，距原点相同为1 km，仍从到等角度排列，得到的干涉信号能量分布函数如图6(c)所示。仍然考虑图6(a)中雷达位置和信号参数，但每个雷达站发射的信号在到达标定点附近会产生在[−,]区间上均匀分布的误差，此时得到的能量分布函数如图6(d)所示。

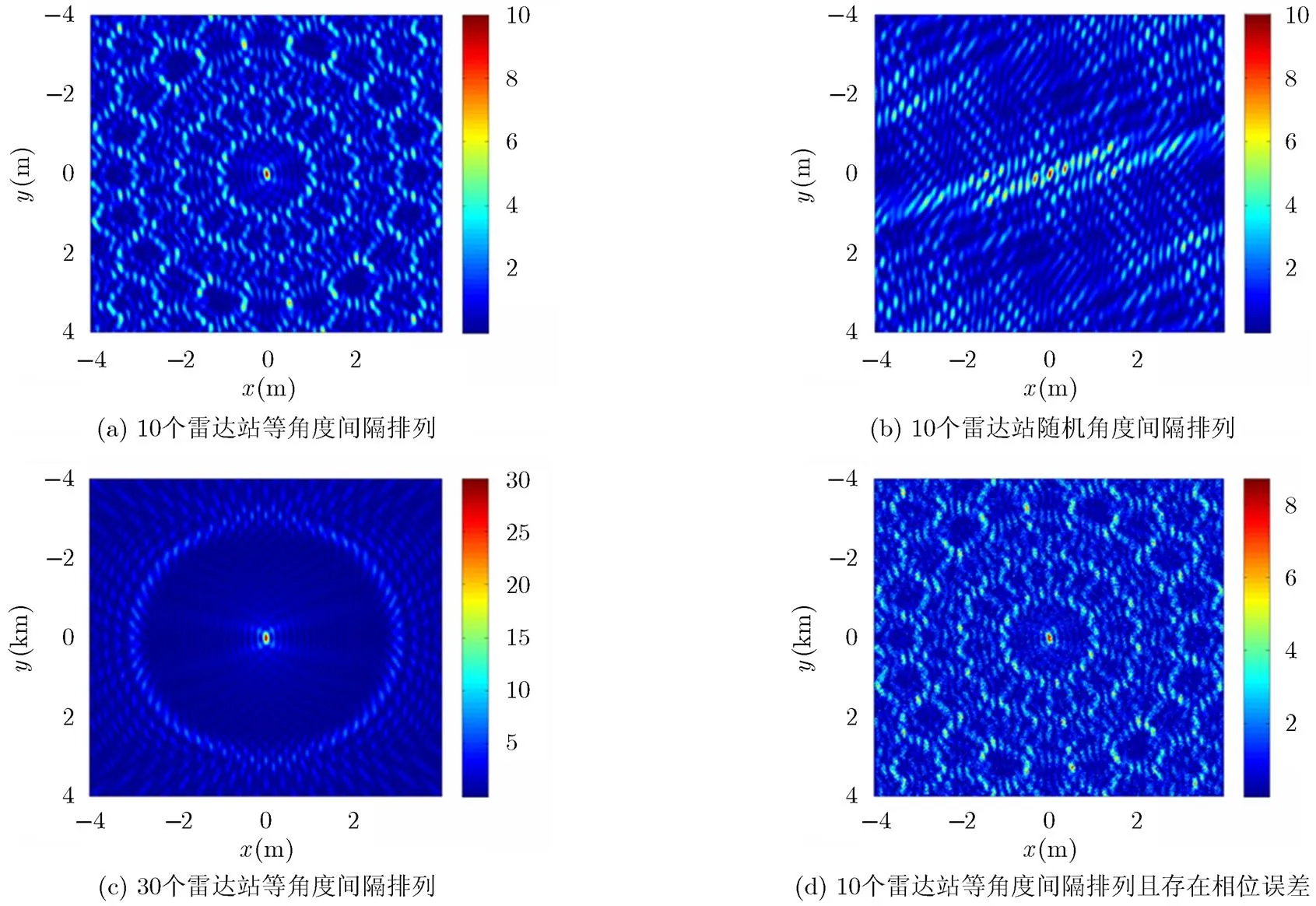
图6 不同参数下空间干涉能量分布图

图6中，当雷达站等角度间隔排列时，在观测场景中只有一个干涉峰点，峰点周围则会出现一些旁瓣，旁瓣水平随发射天线个数增加而减小。当雷达站按随机角度间隔排列时，信号的干涉能量分布会发生显著改变，干涉峰点附近的旁瓣幅度较高，旁瓣的分布无明显的规律，但旁瓣关于干涉峰点对称。由图6(d)可知，干涉斑的大小出现了一定程度的放大，干涉图样变得模糊，毛刺增多，出现误差时，干涉峰点的最大值会降低。

5 结束语

分布式相参发射的原理就是通过雷达发射信号在自由空间的干涉使得在某些空间区域形成干涉峰点，从而提高该处回波信号的信噪比。本文给出了分布式相参发射的原理，定义了干涉信号能量增益分布函数，推导了形成干涉峰点的条件，在近场和远场两种情形下分析了干涉分布函数的特点，表明，对于近天线距离且等间隔布阵的情况，在远场条件下，发射信号在空间能量的分布呈条纹状；对于远天线距离等间距布阵的情况，在近场条件下，若站点数较少，易呈类晶体结构的斑状分布，在远场条件下，若站点个数较多且各发射站已对准标定点，会形成唯一干涉峰点，而旁瓣随天线个数增加而减小。

分布式相参发射在应用时可能存在一些限制。在扫描状态下，为了交替覆盖空间干涉零点，雷达系统的工作方式会变得复杂，尤其是在远天线距离的近场条件下，并且要求雷达接收端具有较高的分辨力能够无模糊地分辨各干涉峰点。在目标跟踪状态下，雷达系统可以预测目标的空间位置，从而只需使发射信号在预测区域形成干涉峰点即可，因此，分布式相参发射更适合工作在跟踪状态下。此时，同样要求雷达接收端能够无模糊地分辨各干涉峰点。跟踪状态下，为了使干涉峰点对准目标，对雷达目标定位精确度要求高；另外，干涉斑的尺寸与雷达工作频率有关，仿真表明干涉斑的大小与雷达波长相当，为了使目标完全位于干涉峰点上，要求干涉斑尺寸不能太小，而目标尺寸不能太大，否则目标可能超出一个干涉峰点的范围从而降低回波能量，所以分布式相参发射的原理更容易在低频率雷达上实现。综上，分布式相参发射对长电磁波、小目标的目标跟踪状态更加有效。

参考文献

[1] 周生华, 刘宏伟. MIMO雷达目标空间和频率散射多样性研究 [J]. 电子与信息学报, 2010, 32(1): 38-42.

Zhou Sheng-hua and Liu Hong-wei. Scattering properties of spatial and frequency diversity of MIMO radar targets[J].&, 2010, 32(1): 38-42.

[2] Fishler E, Haimovich A, Blum R,. MIMO radar: an idea whose time has come[C]. Proceedings of the IEEE Radar Conference, Philadelphia , USA, 2004: 71-78.

[3] Haimovich A M, Blum R S, and Cimini L J. MIMO radar with widely separated antennas[J]., 2008, 25(1): 116-129.

[4] 胡亮兵, 刘宏伟, 刘宝昌, 等. MIMO雷达发射方向图匹配和波形优化方法[J]. 西安电子科技大学学报, 2009, 36(6): 1022-1028.

Hu Liang-bing, Liu Hong-wei, Liu Bao-chang,. Transmit beampattern matching design and waveform optimization for MIMO radar[J]., 2009, 36(6): 1022-1028.

[5] Deng H. Polyphase code design for orthogonal netted radar systems[J]., 2004, 52(11): 3126-3135.

[6] Zhou S H, Liu H W, Zhao Y B,. Target spatial and frequency scattering diversity property for diversity MIMO radar[J]., 2011, 91(2): 269-276.

[7] Fishler E, Haimovich A, and Blum R S. Spatial diversity in radars-models and detection performance[J]., 2006, 54(3): 823-838.

[8] 鲁耀兵, 张履谦, 周荫清, 等. 分布式阵列相参合成雷达技术研究[J]. 系统工程与电子技术, 2013, 35(8): 1657-1662.

Lu Yao-bing, Zhang Lü-qian, Zhou Yin-qing,. Study on distributed aperture coherence-synthetic radar technology[J]., 2013, 35(8): 1657-1662.

[9] 孙培林, 汤俊, 张宁. 分布式相参雷达相参性能的两种监控算法[J]. 清华大学学报(自然科学版), 2014, 54(4): 419-424.

Sun Pei-lin, Tang Jun, and Zhang Ning. Two algorithms for monitoring the coherence performance of distributed coherent radar systems[J]. Journal of(&), 2014, 54(4): 419-424.

[10] 曾涛, 殷丕磊, 杨小鹏, 等. 分布式全相参雷达系统时间与相位同步方案研究[J]. 雷达学报, 2013, 2(1): 105-110.

Zeng Tao, Yin Pi-lei, Yang Xiao-peng,. Time and phase synchronization for distributed aperture coherent radar[J]., 2013, 2(1): 105-110.

[11] Coutts S, Cuomo K, McHarg J,. Distributed coherent aperture measurements for next generation BMD radar[C]. Processings of the Fourth IEEE Workshop in Sensor Array and Multichannel, Waltham, USA, 2006: 390-393.

[12] 陈根华, 陈伯孝, 杨明磊. 分布式相参阵列及其二维高精度方向估计[J]. 电子与信息学报, 2012, 34(11): 2621-2627.

Chen Gen-hua, Chen Bai-xiao, and Yang Ming-lei. High accuracy 2-D angle estimation using distributed coherent arrays[J].&, 2012, 34(11): 2621-2627.

[13] 宋靖, 张剑云, 郑志东, 等. 分布式全相参雷达相干参数估计性能[J]. 电子与信息学报, 2014, 36(8): 1926-1931.

Song Jing, Zhang Jian-yun, Zheng Zhi-dong,. Coherent parameters estimation performance for distributed aperture coherent radar[J].&, 2014, 36(8): 1926-1931.

[14] Yang Yang and Blum R S. Phase synchronization for coherent MIMO radar algorithms and their analysis[J]., 2011, 59(11): 5538-5557.

[15] Huleihel W, Tabrikian J, and Shavit R. Optimal adaptive waveform design for cognitive MIMO radar[J]., 2013, 61(20): 5075-5089.

[16] Kong S, Lee S, Kim C Y,. Wireless cooperative synchronization of coherent UWB MIMO radar[J]., 2014, 62(1): 154-165.

Theory and Performance Analysis of Coherent Transmission for Distributed Radars

Zang Hui-kai Lei Huan Dan Xiao-dong Zhou Sheng-hua Liu Hong-wei

(,,710071,)

By adjusting the transmitting time and the initial phase of distributed radar antennas, the spatial distribution of signal energy transmission can be controlled and then the signal energy can be improved in the spatial region of interest. The fundamentals of distributed coherent transmitting are analyzed, the conditions are presented to form an interference peak, and a spatial interference energy distribution function is defined to represent the gain of the transmitting energy compared to the mean energy, which has a maximum of the number of transmitting antennas. The characteristic of the spatial interference energy distribution function is analyzed in both radar near field and radar far field, indicating that the spatial interference energy distribution function exhibits a stripe shape in radar far field with collocated antennas, and an ellipse shape or a mono-peak shape in radar near field with widely separated antennas. To make a real target contained in a signal interference peak, the distributed coherent transmission works better for lower frequencies and smaller targets in the target tracking mode.

Distributed radar; Distributed coherent transmitting; Spatial interference energy distribution function; Interference peak

TN957

A

1009-5896(2015)08-1801-07

10.11999/JEIT141563

臧会凯 zanghuikai@126.com

2014-12-08收到，2015-03-12改回，2015-06-09网络优先出版

国家自然科学基金(61401329, 61271291, 61372136)资助课题

臧会凯： 男，1990年生，博士生，研究方向为协同探测.

雷 欢： 男，1990年生，硕士生，研究方向为协同探测.

但晓东： 男，1989年生，硕士生，研究方向为协同探测.

周生华： 男，1982年生，博士，副教授，研究方向为MIMO雷达、协同探测.

刘宏伟： 男，1971年生，博士，教授，博士生导师，研究方向为雷达信号处理、雷达系统、雷达自动目标识别等.