光在金属界面传播的实折射角计算

张秋长

(厦门大学嘉庚学院,福建漳州363105)

光在金属界面传播的实折射角计算

张秋长

(厦门大学嘉庚学院,福建漳州363105)

通过对光波矢量分别定义等幅面单位矢量和等相面单位矢量,根据光的传播表达式,分别运用相应的边界条件,并分别求出了光通过介质/金属、金属/介质后的实折射角.通过数值计算可知:对于第1种情况获得的结果与Born和Wolf通过广义的斯涅耳折射定律得到的结果一致;金属/介质的实折射角除了和入射角、介质的折射率、金属的复光学常数有关外,还与金属中等幅面单位矢量和等相面单位矢量的夹角有关,且当2个单位矢量之间的夹角满足一定的关系时,折射角随着入射角的增大出现先增大后减小的现象.

几何光学;光折射;Snell定律;复光学常数;光传输

早在17世纪上半叶,Snell和Descartes就发现当光线穿越由不同介质构成的界面时会发生折射的现象,并总结出了Snell折射定律,成为现代光学原理的重要基础[1].这一定律被广泛应用于理解光在非吸收的透明物质中的传播行为.但当被扩展和应用于强的光吸收材料,如金属边界时,这一问题至今仍未能被很好地认识和理解.

过去的几十年中许多学者对光散射几何光学近似(geometrical optics approximation,GOA)进行了研究[2-13],GOA方法能够克服Mie理论计算大颗粒散射振幅耗时的缺点.而对于吸收性颗粒GOA的研究,存在计算吸收性颗粒中光的传播路径和菲涅尔系数的困难[14],有研究者通过引入有效折射率,提出了在吸收性介质中菲涅耳系数的计算公式,也有研究者将吸收颗粒里的非均匀波近似看作均匀波,给出了弱吸收颗粒近似计算的结果,但对于吸收性稍微强的颗粒,以及强的吸收性颗粒,这种近似不再成立[9,15].因为当光折射入吸收性介质时,对应的折射角是一个复数,必须用等效折射角来描述光的实际传播路径.本文研究了光在金属中的传播以及光在金属界面的折射规律.分别求出了光通过介质/金属、金属/介质边界时的实折射角.2组实折射角的大小均和入射角、介质的折射率、金属的复光学常数有关;此外光入射金属/介质边界时的实折射角还与金属中等幅面单位矢量和等相面单位矢量的夹角有关.

1 光在金属边界的实折射角问题

Born和Wolf根据麦克斯韦方程和边界条件,给出了一组计算公式,用于分析和处理光从介质入射到金属时,已知介质(折射率为na)一侧的入射角θa和金属的光学常数~n=n+iκ,即可计算在金属一侧发生的实折射角[16]:

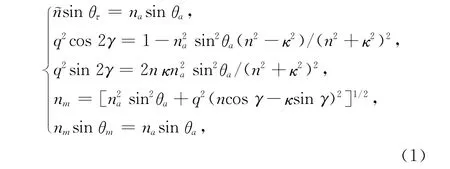
上式中折射角θτ是基于Snell公式的一般意义上在金属一侧的复折射角,nm和θm分别是基于Snell公式的金属等效实数折射率和光在金属一侧的实折射角,q和δ是计算过程中引入的中间参数.假设光从大气(na=1)入射金属银(~n=0.2+i3.44)[2],按公式(1)计算光在金属银一侧的实折射角θm随入射角θa的变化关系,结果如图1所示.当θa较小时,金属银一侧的θm与θa近似成线性变化关系,并且由公式(1)可得sin2θa≈0,nm≈n,与金属折射率的虚部无关.而在大的入射角情况下,θm随θa的变化趋于平坦.

依据同样的原理,Garcia-Pomar等给出了光从金属入射到介质的情况的计算公式,已知金属银一侧的入射角θm,则在介质一侧发生的实折射角θa满足如下关系[17]:

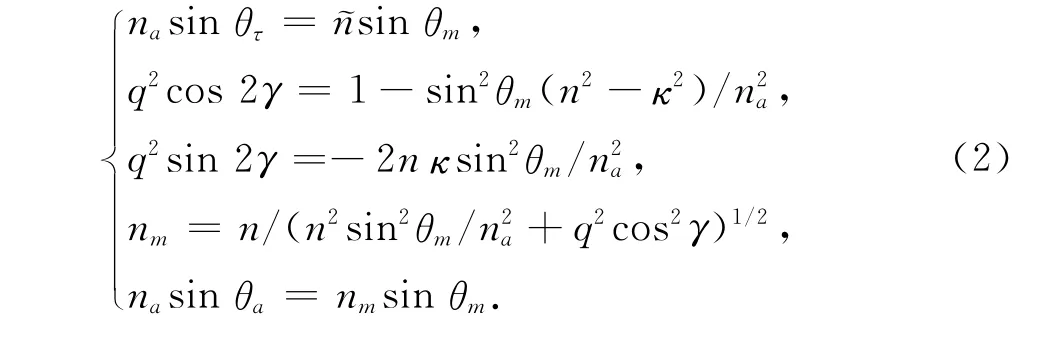
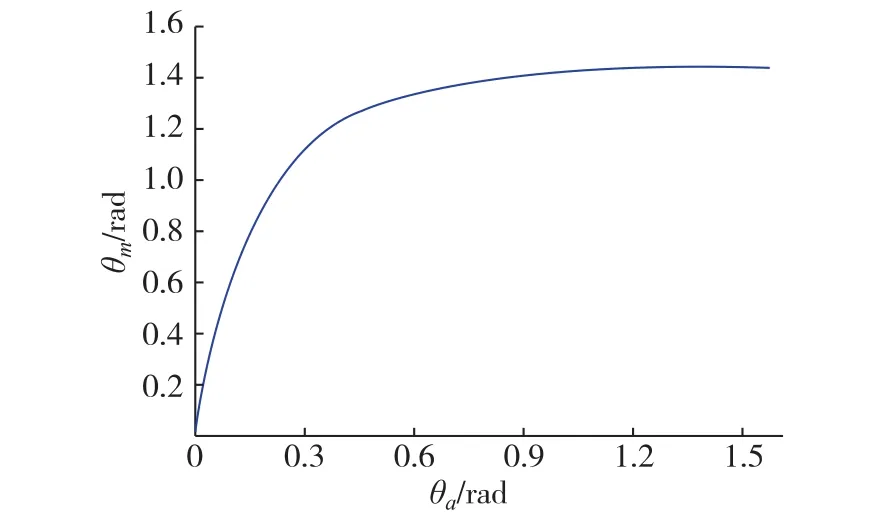
图1 金属银一侧的实折射角θm与大气一侧入射角θa的关系Fig.1 Real refractive angleθm at the silver side shows the relationship with the incidence angleθa at the air side

图2 大气一侧的实折射角θa与银一侧的入射角θm的关系Fig.1 Real refractive angleθa at the air side shows the relationship with the incidence angleθm at the silver side

当光在金属银中以入射角θm穿过银和大气的界面时,按式(2)计算出光在大气一侧的折射角θa随入射角θm的变化关系,结果显示在图2中.由图2可知,大气一侧的出射角θa与银一侧的实入射角θm具有图1中类似的变化关系.若假设光从介质一侧入射,穿过平行的金属银膜,发生实折射角,又以该折射角作为入射角,从介质一侧出射,由于式(1)、(2)中的等效折射率nm具有不同的表达式,可知介质一侧的出射角并不等于初始入射角.从图1中可知,当大气一侧的入射角为0.6 rad时,金属银一侧的实折射角约等于1.3 rad,而在图2中,若以1.3 rad作为金属银一侧的入射角,在大气一侧的折射角约为0.055 rad,约是初始入射角的1/10,这与实验观察的结果不一致,即介质一侧的出射角应等于初始入射角,所以上述模型具有一定的局限性.虽然2组公式都基于相同的原理,但是由于第2组计算公式入射角是复数角,而处理过程代入计算的是实数角度,忽略了复数角对折射角的影响.所以利用2种模型得到的结果和实验结果不一致.为了获得和实验结果一致的理论模型,本文通过对光波矢量定义等幅面单位矢量和等相面单位矢量,根据光的传播表达式,分别运用相应的斯涅耳折射定律,求解得到光在金属界面发生的实折射角,通过分析获得理论和实验的统一.

2 光从介质入射到金属的实折射角

光波在金属中的传播如图3所示,它的等幅面一般不与等相面重合,这样的波称为非均匀波,等幅面和等相面的单位矢量分别为q和s,两单位矢量之间的夹角为ξ=cos-1(q·s).把平面电磁波E(r,t)= E(r)e-iωt,H(r,t)=H(r)e-iωt代人麦克斯韦方程,可以得到光波在金属中满足如下方程[16]:

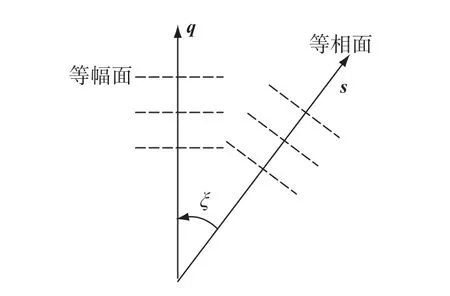
图3 光在金属中的传播Fig.3 Light propagation in metal

从式(4)可知金属的复光学常数并不是真正的物质常数,而是随入射光的频率改变.虽然根据经典电磁理论,只有厚度异常薄的金属样品才能让入射光有所透过,但在金属自由电子气的Drude模型中,当光的频率足够大,可预期金属的光学行为基本上如同介电质,比如有些金属在长波区不透明并且反射高,而在可见和紫外的某一临界波长,它们变得透明[16,18].

同时金属中的光波可表示成:

相位常数、衰减常数与光学常数的实部、虚部之间的关系如下:

由于n,κ均不为0,从上式可知,ξ≠π/2,即两单位矢量不会垂直.经计算可得:

设入射波为均匀平面电磁波,Ei(r)=E0i· e-iksi s i·r,其中ksi=nik0(ni为介质的折射率),为简便起见,考虑入射波在入射面yz平面内,如图4所示.

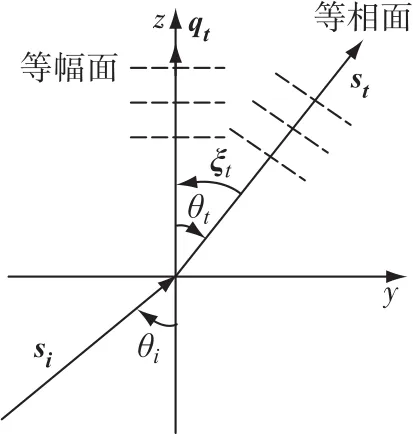
图4 光在金属中界面的折射与传播Fig.4 Light propagation and its refraction at the metal interface

其中入射角为θi,折射角为θt,ξt为z轴和qt的夹角,两单位矢量之间的夹角ξt=cos-1(qt·st),则根据相位的连续性可知,折射波的等幅面单位矢量和等相面单位矢量也均在入射面yz平面内,由于两单位矢量不可能垂直,从图4可知折射角θt肯定小于π/2,并且存在:

根据式(9)可得折射到金属的实折射角θt如下:

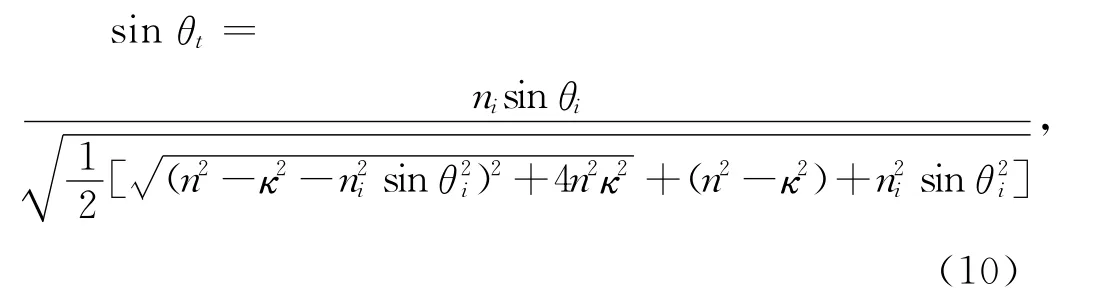
从式(10)可知,折射到金属的实折射角θt和入射角、介质的折射率、金属的复光学常数有关.若用等效折射率nm表示式(10)中的平方根,则式(10)可以表示成斯涅耳定律的形式.nm除了取决于表征金属的物理量,而且还取决于入射角.

图5 金属银一侧的实折射角θt与大气一侧入射角θi的关系Fig.1 Real refractive angleθt at the silver side shows the relationship with the incidence angleθi at the air side

按公式(10)计算光在金属银一侧的实折射角θt随大气一侧入射角θi的变化关系,结果如图5所示.对比图5和图1可知两曲线完全一致,说明新的处理方法与Born和Wolf得到的结果一致.

3 光从金属入射到介质的实折射角

对于光从金属入射到介质,考虑折射后的波为E′(r)=E′0·e-i(k′sts′t+ik′qt q′t)·r,考虑入射波在入射面yz平面内(如图6所示),入射角为θ′i,入射波等幅面单位矢量和法线的夹角为ζ′i,折射角为θ′t,折射波等幅面单位矢量和法线的夹角为ζ′t,折射波两单位矢量之间的夹角ξt′=cos-1(q′t·s′t),由于金属中波的相位波矢和衰减波矢在界面上均有切向分量,所以折射波的相位常数k′st,衰减常数k′qt之间的关系如下:

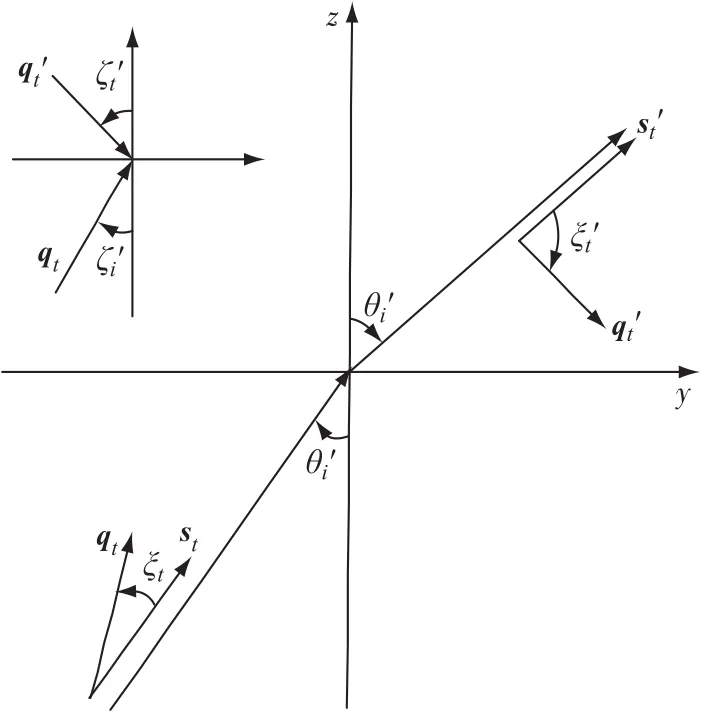
图6 光从金属折射到介质Fig.6 Light refraction from metal into medium

从式(11)可知,折射后的波为非均匀平面波,等幅面单位矢量q′t和等相面单位矢量s′t之间的夹角ξ′t=π/2,即两单位矢量相互垂直.

同理,由边界条件可知:

由式(11)、(12)可得折射到介质中的实折射角θ′t由下式决定:

从式(13)可知,如果只给出与式(2)相同的已知条件,则式(13)计算不出实折射角的大小,因为在介质一侧的实折射角除了和入射角、介质的折射率、金属的复光学常数有关外,还与金属中光波的等幅面单位矢量和等相面单位矢量的夹角有关,这是公式(2)没有考虑的参数.

假设当光从金属银(~n=0.2+i3.44)入射大气(ni=1)界面时,按公式(13)计算,分别考虑ζ′i=θ′i,ζ′i= θ′i/2,ζ′i=0时折射角θ′t随入射角θ′i变化关系,从图7可知对于ζ′i=θ′i,曲线和图2非常吻合,说明公式(2)只是式(13)的特殊情况,即等幅面和等相面相互平行;而当ζ′i=θ′i/2时,由图可知折射角θ′t随入射角θ′i增大出现先增加后减小的现象,若以1 rad作为金属银一侧的入射角,由图可得在大气一侧的折射角约分别为0.05 rad、1 rad,由此可知两单位矢量之间的夹角ξ=cos-1(q·s)的大小对折射角大小的影响很大.所以当光波在金属中的等幅面与等相面重合(均匀光波),可以使用公式(2)进行计算,而对于更一般的情况还需考虑等幅面单位矢量和等相面单位矢量的夹角对实折射角的影响,此时需要使用式(13)进行计算.

图7 大气一侧的实折射角θ′t与银一侧的入射角θ′i的关系Fig.7 Real refractive angleθ′t at the air side shows the relationship with the incidence angleθ′i.

当ζ′i=0时,即等幅面单位矢量qt垂直入射界面,此时由于金属中波的衰减波矢在界面上的切向分量为零,所以折射波的波矢为一实数k′st=nik0,此时折射波为均匀波,相应的边界条件式(12)变为如下:

若光从介质一侧入射,穿过平行的金属膜,发生折射,从大气一侧出射,综合式(9)、(14)可知θi等于θ′t,即大气一侧的出射角等于初始入射角.这与实验观察到大气一侧的出射角等于初始入射角的结果一致.

4 结 论

本文通过对光波矢量分别定义等幅面单位矢量和等相面单位矢量,研究了光在金属中的传播.对两矢量运用相应的边界条件,分别求出光通过介质/金属、金属/介质边界时的实折射角.光通过介质/金属的实折射角与入射角、介质的折射率、金属的复光学常数有关;而光入射金属/介质边界时的实折射角除了和入射角、介质的折射率、金属的复光学常数有关外,还与金属中等幅面单位矢量和等相面单位矢量的夹角有关,当两单位矢量的夹角按一定的规律变化,折射角随着入射角的增大先增大后减小;均匀光波从介质一侧入射,穿过金属膜,发生实折射角,又以该实折射角作为入射角,从介质一侧出射,则介质一侧的出射角并不是一个确定的值,还必须给出等幅面单位矢量和等相面单位矢量的夹角才能确定出射角的大小.

[1] Shirley J W.An early experimental determination of Snell′s law[J].American Journal of Physics,1951,19 (9):507-508.

[2] Davis G E.Scattering of light by an air bubble in water [J].Journal of the Optical Soc Am,1955,45(7):572-581.

[3] van de Hulst H C.Light scattering by small particles [M].New Xork:John Wiley&Sons,1957.

[4] Glantschnig W J,Chen S H.Light scattering from water droplets in the geometrical optics approximation[J].Appl Opt,1981,20,2499-2509.

[5] Ungut A,Grehan G,Gouesbet G.Comparisons between geometrical optics and Lorenz-Mie theory[J].Appl Opt, 1981,20:2911-2918.

[6] Hovenac E A.Calculation of far-field scattering from nonspherical particles using a geometrical optics approach [J].Appl Opt,1991(30):4739-4746.

[7] Xu F,Cai X Sh,Ren K F.Geometrical-optics approximation of forward scattering by coated particles[J].Appl Opt,2004,43:1870-1879.

[8] Aden A L,Kerker M.Scattering of electromagnetic waves by two concentric spheres[J].J Appl Phys,1951,22: 1242-1246.

[9] Li X Zh,Han X E,Li R X,et al.Geometrical-optics approximation of forward scattering by gradient-index spheres[J].Applied Optics,2007,46(22):5241-5247.

[10] Xu H T,Shen J Q,Wei X H.Geometrical optics approximation of light scattering by large air bubbles[J].Particuology,2008(6):340-346.

[11] 徐峰,蔡小舒,沈嘉祺.米氏理论的近似及在粒度测量中的应用[J].光学学报,2003,23(12):1464-1469.

[12] 吕且妮,徐畅,靳文华.基于几何光学近似模型的大气泡粒子散射光场分布计算[J].天津大学学报:自然科学版,2013,45(12):1089-1095.

[13] 李祥震,韩香娥.利用几何光学近似计算GI-POF的前向散射[J].红外与激光工程,2011,40(6):1098-1100.

[14] Xang P,Liou K N.Light scattering by hexagonal ice crystals:comparison of finite-difference time domain and geometric optics models[J].J Opt Soc Am:A,1995,12 (1):162-176.

[15] Xu F,Cai X Sh,Ren K F.Geometrical optics approximation of forward scattering by coated particles[J].Appl Opt 2004,43:1870-1879.

[16] 马科斯·波恩,埃米尔·沃尔夫.光学原理[M].5版.杨葭荪,译.北京:科学出版社,1978.

[17] Garcia-Pomar J L,Nieto-Vesperinas M.Transmission study of prisms and slabs of lossy negative index media [J].Opt Exp,2004,12(10):2081-2095.

[18] Wooten F.Optical properties of solids[M].New Xork: Academic Press,1972.

The Calculation of the Refraction Angle of Light Propagation at Metal Interface

ZHANG Qiu-zhang
(Xiamen University Tan Kah Kee College,Zhangzhou 363105,China)

The light propagation within a metal and the refraction at the interface of metals are studied.On the basis of unit vectors denoting the planes of constant field amplitude and constant phase,respectively,the light propagation and attenuation are described by the complex refractive index of the metal and the angle between the unit vectors,with the expression for the light propagation. Subject to corresponding boundary conditions,refractive angles of the light through the metal/medium and medium/metal interface have been obtained.The numerical analysis shows that resutls for the metal/medium case agree with those the Born and Wolf using snell′s law.The angle of refraction metal/medium depend not only on the incident angle,the refractive index of medium,and the complex refractive index of metal,but also on the angle between the planes of constant amplitude and of constant phase.While the angle between the two unit vectors satisfies a certain relation,the angle of refraction increases first and then decreases with the increase of incident angle.

geometric optics;light refraction;Snell law;complex optical constants;light propagation

10.6043/j.issn.0438-0479.2015.02.016

O 435

A

0438-0479(2015)02-0242-05

2014-02-20 录用日期:2014-05-29

Email:zqzhang@xujc.com

张秋长.光在金属界面传播的实折射角计算[J].厦门大学学报:自然科学版,2015,54(2):242-246.

:Zhang Qiuzhang.The calculation of the refraction angle of light propagation at metal interface[J].Journal of Xiamen U-niversity:Natural Science,2015,54(2):242-246.(in Chinese)