不同饱和度下破碎软岩隧道掌子面破坏范围上限分析

杨子汉，杨小礼，张佳华，李永鑫



不同饱和度下破碎软岩隧道掌子面破坏范围上限分析

杨子汉，杨小礼，张佳华，李永鑫

(中南大学土木工程学院，湖南长沙，410075)

基于构建的隧道掌子面二维多块体滑移破坏模式，将非线性Hoek−Brown准则与软岩强度随饱和度变化关系相结合，借助极限分析原理和数值优化手段，提出一种在不同饱和度下估算隧道掌子面破坏范围的计算方法。以广西瑶寨隧道突水突泥事故作为算例，计算得到不同饱和度下隧道掌子面的破坏范围。研究结果表明：岩体的抗压强度随饱和度的提高逐渐减小，且通过参数转换得到的黏聚力与内摩擦角也随之减小；隧道掌子面破坏范围和支护力随饱和度的增大而增大；当饱和度为0.8时，破坏面已延伸至地表，此时维持掌子面稳定的最小支护压力为651.541 kPa；在破坏面扩大延伸的过程中，若不采取相应的处理措施，则隧道掌子面将产生突水突泥、塌方等地质灾害。该方法最大的优点是凭借少量的试验参数就能确定隧道掌子面的破坏范围，可作为隧道设计施工中的一种估算方法。

破碎软岩；隧道掌子面；饱和度；上限分析；突水突泥

软岩不仅易风化、强度低，而且具有遇水软化的特性。当地表雨水入渗或者地下水迁移至软岩地层，其强度会大大降低，这对穿越软岩地层隧道的稳定性提出了很高的要求。对于软岩遇水软化规律，Hawkins等[1]通过单轴试验，测得了15种砂岩在不同含水率下的抗压强度，并由此建立了砂岩单轴抗压强度与含水率的关系表达式。Vasarhelyi等[2−3]在Hawkins等[1]的基础之上，对表达式进行了改进，提出用饱和度参数代替含水率，从而解决了不同种类岩石在完全饱和时含水量存在较大差异的问题。周翠英等[4−5]通过室内试验测得了红色砂岩、泥岩、黑色炭质泥岩等几种典型软岩在不同饱水时间点的强度参数，并借助曲线拟合手段得到软岩强度随饱水时间服从指数变化规律。隧道掌子面破坏范围的研究属于隧道稳定性研究的一个分支，研究方法主要有极限平衡法、滑移线法、模型试验、数值模拟、极限分析法[6]等。与其他方法相比，极限分析计算过程简单、快捷，计算结果较准确，所以，近几年在分析岩土稳定性问题中运用较广泛，如：Mollon等[7]通过计算得到了隧道掌子面崩落压力的上限解，并运用空间离散化技术改进了用于上限计算的隧道掌子面破坏模式；Yang等[8−10]针对极限分析理论提出了适用于非线性破坏准则的切线法，并对隧道、边坡、地基基础等岩土结构稳定性问题进行了研究。本文基于极限分析上限定理与非线性Hoek−Brown破坏准则，根据构建的掌子面二维多块体滑移破坏模式，提出在不同饱和度情况下计算软岩隧道掌子面破坏范围的一种方法。借助具体算例，探讨饱和度对转换强度参数、隧道掌子面支护力以及破坏范围的影响。最后根据数值优化结果得出隧道掌子面的破坏范围。

1 基本原理与定义

1.1 Hoek−Brown破坏准则

自1980年适用于岩石的Hoek−Brown(H−B)破坏准则被提出以来，该破坏准则受到了国内外学者的广泛认可，并且在诸多工程实践中得到了验证[11−12]。起初，H−B破坏准则仅适用于完整的、没有节理的坚硬岩石。为了拓宽破坏准则的应用范围，Hoek和Brown引入能够反映岩石软硬、节理数量、开挖扰动程度等参数并予以改进[13]，可适用于低应力且质量较差的岩体。改进的H−B破坏准则的表达式为

其中：1和3分别为破坏时的最大、最小主应力；ci为完整岩石的单轴抗压强度；b，和为量纲一的材料常数。

其中：i为反映岩体软硬程度的参数，通过岩芯柱状式样的三轴试验或者查表估算获得，一般为5~40；GS为地质强度指标，反映不同地质条件下的岩体强度，根据岩体岩性、结构、节理数量等因素综合评定，取值范围为0~100；为节理岩体扰动参数，反映爆破和应力松弛对节理岩体产生扰动的程度，取值为0~1，未受到扰动的岩体取值为0；反映岩体的完整程度；为表征节理的岩体参数。

值得注意的是：令3=0，可得到完整岩石单轴抗压强度ci与岩体单轴抗压强度c之间的关系表达式，即c=ci·s。因此，在一些不能直接测得完整岩石单轴抗压强度时，可以通过岩体的单轴抗压强度予以估算。

1.2 Hoek−Brown与Mohr−Coulomb破坏准则间参数转换

由于本文采用的是极限分析原理中经典的块体滑移破坏模式，相邻块体之间存在不连续的速度间断线，无法直接运用积分与变分原理求出破坏模式的内能耗散功率，所以，需要将非线性的Hoek−Brown破坏准则转化为线性的Mohr−Coulomb(M−C)破坏准则进行计算。两者之间的转化方法主要有瞬时切线法[10]和最佳曲线拟合法[13]2种。前者是将H−B破坏准则包络线上指定点的切线方程作为转化后的M−C破坏准则的表达式，该方法方便、简单、快捷，但在有效正应力较小的情况下，切线法的计算精度不高；后者则借助最小二乘法，在抗拉强度t与最大围压上限3max之间，依据等面积思想将曲线形的H−B准则转化为线性的M−C准则(见图1)。其强度参数黏聚力和内摩擦角的转换表达式为

图1 H−B准则与M−C准则转换示意图

Fig. 1 Schematic diagram of transformation between H−B and M−C failure criterion

1.3 岩体强度随饱和度变化关系

岩体的饱和度(r)是影响岩体强度的重要因素之一，特别是对于软岩。当饱和度达到临界值时，饱和度的小幅度增长可能会引起软岩强度明显下降，甚至造成结构物失稳破坏。Vasarhelyi等[2]结合前人研究成果，提出饱和度与岩体强度的最佳拟合公式：

式中：c(r)为不同饱和度下的岩体单轴抗压强度；，和为拟合参数，可由岩体单轴干抗压强度c0与饱和单轴抗压强度csat确定，

由此通过简单的室内实验获得岩体的单轴干抗压强度c0与饱和抗压强度csat，结合H−B破坏准则与M−C破坏准则之间的参数转换公式，可以计算不同饱和度时岩体的强度参数。

2 隧道掌子面破坏范围上限计算

2.1 破坏模式的确定

(a) 整体破坏模式；(b) 局部三角形滑块

图2 隧道掌子面破坏模式

Fig. 2 Failure mode of tunnel face

2.2 支护压力计算

1) 各刚性滑块之间的速度矢量关系如图3所示，由此确定速度矢量之间的数值关系如下：

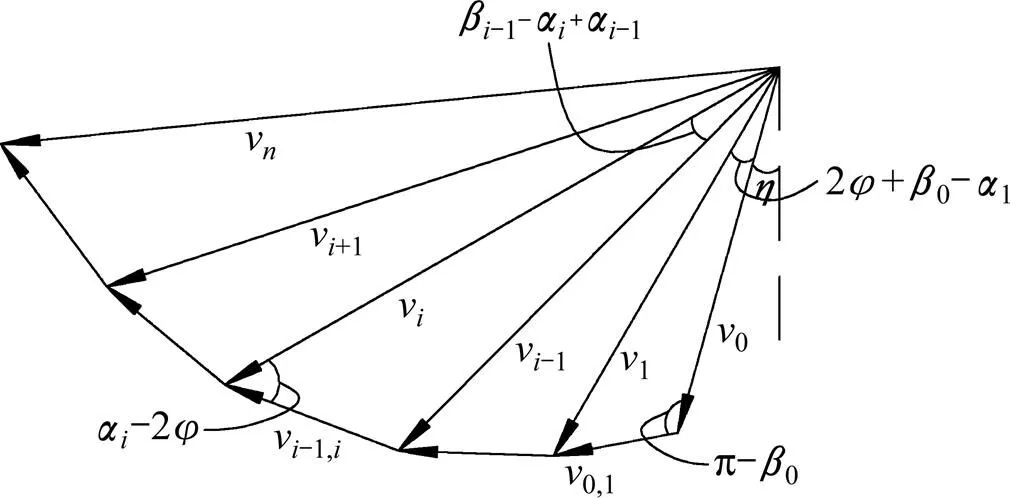
图3 破坏模式速度矢量关系图

依据破坏模式的几何关系确定速度间断线之间的长度关系如下：

各刚性三角形滑块面积为

2) 依据极限分析上限原理，重力做功功率为

(10)

支护力功率为

速度间断线上的内能耗散功率可表示为

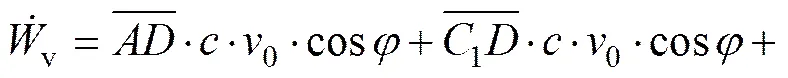
4) 依据虚功原理，即外力做功等于内能耗散，可获得支护力上限解的表达式：

2.3 边界约束条件

为保证破坏模式中的三角形刚性块不发生扭曲畸变且满足几何条件，依据破坏模式几何关系以及速度矢量关系，可施加如下约束边界条件：

2.4 掌子面破坏范围

借助Matlab优化工具，以掌子面支护压力为优化对象，通过编程计算可以得到在某一已知强度参数条件下维持隧道掌子面稳定的最小合理支护压力。而每一个优化出的支护压力对应着一组未知数的解，即α，β，和0。由此，可基于本文提出的二维破坏模式制定隧道掌子面的破坏范围。

3 算例分析

瑶寨隧道位于广西“六宜高速”南丹县段，全长2.7 km。隧道穿越长约14 km的第三系断层。断层区域岩性以图4所示粉砂岩为主，且在风化裂隙及卸荷裂隙影响下，岩体破碎，存在相当规模的碎石夹土。一般地，第三系粉砂岩呈红黄色和灰白色，薄层至块状构造，且具有遇水软化的特性，属于软弱岩体。

图4 瑶寨隧道第三系破碎粉砂岩照片

2011−02−12，瑶寨隧道下行线(左洞)掌子面ZK47+067处发生大规模突泥地质灾害。泥沙突入隧道，淤积长度约200 m，1 h后，隧道掌子面正上方地表发生塌陷，形成塌陷坑。本文以此作为算例，研究其隧道掌子面的塌落范围。

3.1 计算参数的确定

依照本文推导方法，计算瑶寨隧道掌子面破坏范围所需的基本参数有：该区段隧道埋深、第三系破碎粉砂岩容重、干单轴抗压强度c0、饱和单轴抗压强度csat、粉砂岩的硬度指标i、节理岩体扰动参数以及地质强度指标GS。

，，c0以及csat可由设计参数和室内实验获得，取值分别为：=64 m，=22.2 kN/m3，c0=25 MPa，csat=0.22 MPa。i，和GS为Hoek−Brown破坏准则的量纲一的参数，通过查表[14]可知粉砂岩的硬度指标i=7±2，本文取平均值7。由于瑶寨隧道在该区段采用三台阶预留核心土的机械开挖方式，根据Heok的建议[13]，=0.7；结合现场实际观测情况(如图4所示)，地质强度指标GS采用文献[14]中的估算方法，GS的取值范围为15~35，计算中取GS=25。

在获取基本参数后，根据式(3)和式(5)便可以计算出瑶寨隧道第三系破碎粉砂岩在不同饱和度下的抗压强度c(r)与转换后的强度参数(,)，计算值见表1。根据表1中数据绘制强度折减曲线以及和变化曲线分别如图5和图6所示。

1—粉砂岩强度σ(Sr)；2—强度折减百分比累积百分数

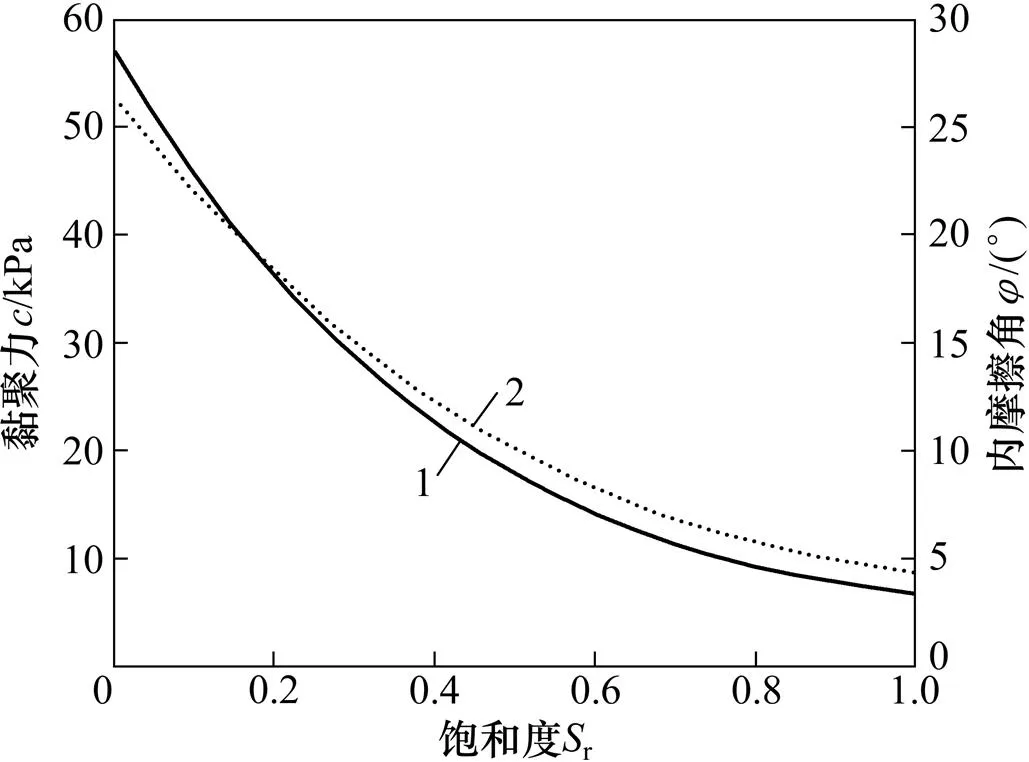
1—c；2—φ

从表1可以看出：岩体的抗压强度随饱和度r的增加逐渐减小；当饱和度较低，r=0.1~0.3时，抗压强度折减趋势明显。从图5可以看到：当岩体的饱和度r=0.4时，岩体的抗压强度减小到无水情况下的1/10左右；当岩体饱和度较高，r=0.6~1.0时，随着饱和度的增加，强度折减趋势趋于平缓。从图6可见：强度参数(,)的变化与抗压强度折减趋势相似。

表1 不同饱和度下破碎粉砂岩强度参数

3.2 优化计算结果

由于本文提出的破坏模式中的滑块数量是未知的，所以，需要先根据具体的算例参数确定最佳的滑块数量，以保证计算结果的精确性。这里采用r=0.20时的强度参数，即=36.37 kPa，=12.22°，c(r)=8.38 MPa。不同滑块数量对应的隧道掌子面支护力计算值如表2所示。从表2可以看出：随着滑块数量的增加，支护力cr逐渐减小并趋于稳定；但当滑块的数量超过7时，支护力却在缓慢递增。因此在本算例中，滑块数量的最佳取值为7。

表2 不同滑块数量对应的隧道掌子面支护力上限解

在确定强度参数和滑块数量后，运用极限分析上限定理和Matlab优化程序，按照文中推导过程，可优化出各饱和度下隧道掌子面最小支护力cr和各个未知角度。优化结果如表3所示。

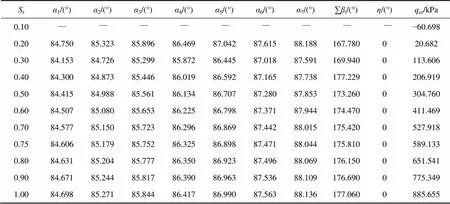
表3隧道掌子面支护力与各角度优化结果

从表3可见：当r=0.10时，隧道掌子面支护力的优化结果为负值，说明支护力的方向与破坏模式中假设方向相反。也就是说，在这种情况下，隧道掌子面即使没有施加支护力也不会产生失稳破坏；随着饱和度r的增加，支护压力数值由负转正，且在不断增大，当完全饱和r=1.0时，维持掌子面稳定的支护压力达到885.655 kPa。需注意的是：在各个参数下的优化值都为0°，说明在该破坏模式下，顶部三角形滑块在失稳时的速度矢量始终沿竖直方向。

利用优化结果的各个角度与当前饱和度下的内摩擦角可以绘制出瑶寨隧道在不同饱和度下的掌子面破坏范围。本文绘制出了饱和度r分别为0.20，0.70，0.75，0.80和1.00的掌子面破坏范围，见图7。

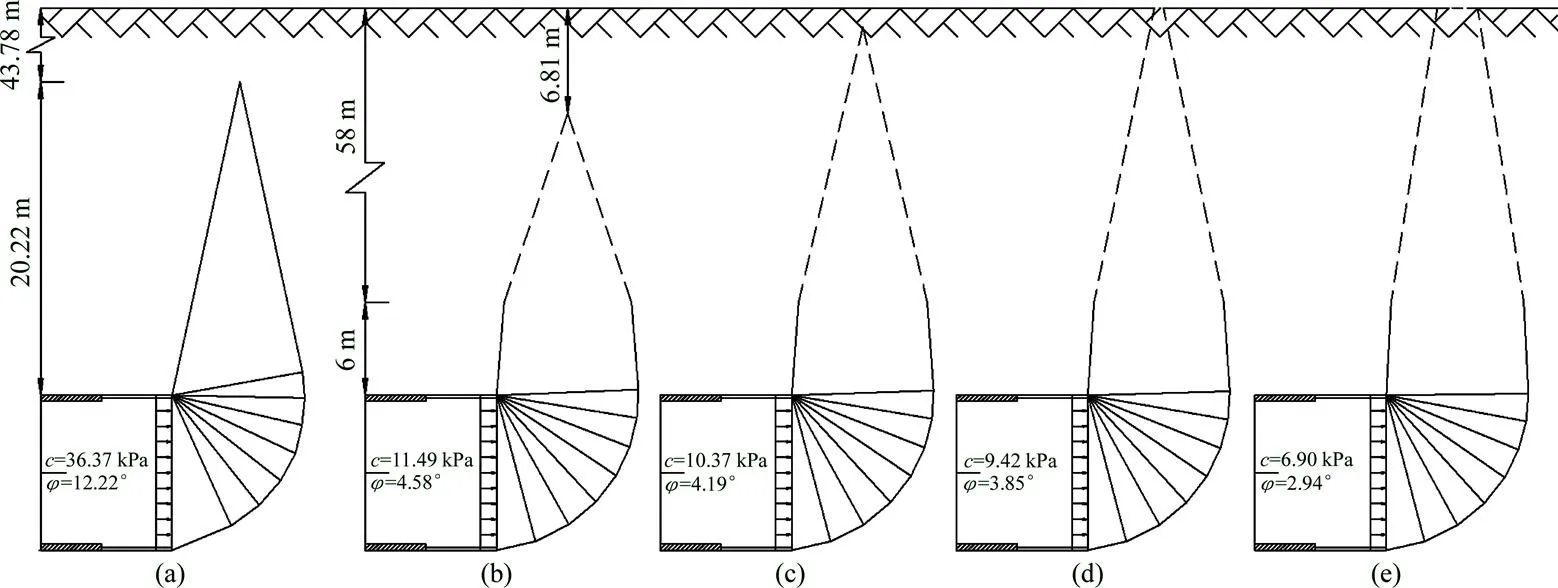
Sr：(a) 0.20；(b) 0.70；(c) 0.75；(d) 0.80；(e) 1.00

从图7可见：随着饱和度的提高，掌子面的破坏范围明显扩大，且沿纵向向地表逐渐延伸。从饱和度r=0.8时的破坏范围(图7(d))可以看出，此时破坏面已经延伸至地表。对于瑶寨隧道，强降雨带来了充足的水源补给，使断层带破碎粉砂岩逐渐达到饱和，强度大大降低。加之隧道停滞施工，支护跟进不及时，最终导致突水突泥地质灾害发生。

4 结论

1) 岩体的强度参数与饱和度密切相关。岩体的抗压强度随饱和度提高逐渐减小，且通过参数转换得到的和也随之减小。大致以饱和度r=0.40为界，当饱和度大于0.40时，强度参数折减趋势趋于平缓。

2) 隧道掌子面破坏范围与支护力都随饱和度的提高而增大。当饱和度r=0.80时，破坏面已延伸至地表，此时所需维持掌子面稳定的最小支护压力为651.541 kPa。在破坏面从产生、逐渐扩大直至延伸到地表的整个过程中，若不采取相应的处理措施，隧道掌子面将很可能产生突水突泥、塌方等地质灾害。

[1] Hawkins A B, Mcconnell B J. Sensitivity of sandstone strength and deformability to changes in moisture content[J]. Quarterly Journal of Engineering Geology and Hydrogeology, 1992, 25(2): 115−130.

[2] Vasarhelyi B, Van P. Influence of water content on the strength of rock[J]. Engineering Geology, 2006, 84(1/2): 70−74.

[3] Vasarhelyi B. Statistical analysis of the influence of water content on the strength of the miocene limestone[J]. Rock Mechanics and Rock Engineering, 2005, 38(1): 69−76.

[4] 周翠英, 朱凤贤, 张磊. 软岩饱水试验与软化临界现象研究[J]. 岩土力学, 2010, 31(6): 1709−1715. ZHOU Cuiying, ZHU Fengxian, ZHANG Lei. Research on saturation test and softening critical phenomena of soft rocks[J]. Rock and Soil Mechanics, 2010, 31(6): 1709−1715.

[5] 周翠英, 邓毅梅, 谭祥韶, 等. 饱水软岩力学性质软化的试验研究与应用[J]. 岩石力学与工程学报, 2005, 24(1): 33−38. ZHOU Cuiying, DENG Yimei, TAN Xiangshao. Experimental research on the softening of mechanical properties of saturated soft rocks and application[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(1): 33−38.

[6] Chen W F. Limit analysis and soil plasticity[M]. Netherland: Elsevier, 2013: 37−39.

[7] Mollon G, Dias D, Soubra A. face stability analysis of circular tunnels driven by a pressurized shield[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(1): 215−229.

[8] Yang X L, Huang F. Collapse mechanism of shallow tunnel based on nonlinear Hoek−Brown failure criterion[J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686−691.

[9] Yang X L, Zhang J H, Jin Q Y, et al. Analytical solution to rock pressure acting on three shallow tunnels subjected to unsymmetrical loads[J]. Journal of Central South University, 2013, 20(2): 528−535.

[10] Yang X L, Yin J H. Slope equivalent Mohr–Coulomb strength parameters for rock masses satisfying the Hoek−Brown criterion[J]. Rock Mechanics and Rock Engineering, 2010, 43(4): 505−511.

[11] 朱合华, 张琦, 章连洋. Hoek−Brown强度准则研究进展与应用综述[J]. 岩石力学与工程学报, 2013, 32(10): 1945−1963. ZHU Hehua, ZHANG Qi, ZHANG Lianyang. Review of research progresses and applications of hoek-brown strength criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 1945−1963.

[12] 杨小礼. 岩石极限分析非线性理论及其应用[J]. 中南大学学报(自然科学版), 2009, 40(1): 225−229. YANG Xiaoli. Limit analysis with nonlinear failure criterion in rock masses and its applications[J]. Journal of Central South University (Science and Technology), 2009, 40(1): 225−229.

[13] Hoek E, Carranza C, Corkum B. Hoek-Brown failure criterion:2002 edition[C]//Hammah R, Bawden W F, Curran J. Proceedings of the North American Rock Mechanics Society NARMS-TAC 2002.Toronto, Canada: University of Toronto Press, 2002: 267−273.

[14] Hoek E, Brown E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165−1186.

(编辑 陈灿华)

Upper bound analysis of collapsing area of tunnel face in broken soft rocks under different saturations

YANG Zihan, YANG Xiaoli, ZHANG Jiahua, LI Yongxin

(School of Civil Engineering,Central South University, Changsha 410075, China)

Based on the multi-blocks failure mechanism, a computing method for estimating the scale of the collapsing area of the tunnel face under different degrees of saturation was proposed by non-linear Hoek−Brown failure criterion and the relationship between the strength of soft rocks and saturation. Taking the accident of water gushing and mud outburst in Yaozhai Tunnel as an example, the scope of the collapsing area in the front of the tunnel face was computed under different degrees of saturation. The results show that the compressive strength of rock decreases gradually with the increase of the degree of saturation, so does the cohesion and internal friction angle which is obtained by the parameter transformation. However, both the scale of collapsing area of the tunnel face and the supporting forces tend to increase with the increase of the saturation. When the saturation is 0.8, the failure surface extends to the earth’s surface and the supporting force approaches 651.541 kPa. Moreover, some geological disasters such as water gushing, mud gushing and the landslides will occur if the failure surface extends without any protective measurement. The greatest advantage of this proposed method is that the range of the collapsing area of the tunnel face can be determined even based on a few experimental parameters, which can be regarded as a kind of estimating approach for tunnel design and construction.

broken soft rocks; tunnel face; degree of saturation; upper bound analysis; water gushing and mud outburst

10.11817/j.issn.1672-7207.2015.06.039

U 451

A

1672−7207(2015)06−2267−07

2014−10−08；

2014−12−22

国家自然科学基金资助项目(51178468; 51378510)；湖南省研究生科研创新资助项目(CX2014B069)(Projects (51178468; 51378510) supported by the National Natural Science Foundation of China; Project (CX2014B069) supported by Graduated Student Research and Innovation Project of Hunan Province)

杨子汉，博士研究生，从事隧道工程研究；E-mail：134801042@csu.edu.cn