岩体可爆性分级的未确知均值分级方法及应用

戴兵，赵国彦，董陇军



岩体可爆性分级的未确知均值分级方法及应用

戴兵，赵国彦，董陇军

(中南大学资源与安全工程学院，湖南长沙，410083)

将未确知测度理论应用到岩石可爆性分级问题中，提出未确知均值分级方法，建立岩石可爆性分级的未确知均值分级模型；选用岩石容重、岩石抗拉强度、岩石完整性系数作为分级模型的判定指标；以14种岩石的实测判定指标建立分类判别指标的未确知测度函数，并求得各分级样本指标的平均值和单指标测度矩阵；根据信息熵理论确定各指标的权重，利用置信度识别准则对岩石进行判定分级。利用该模型对矿区岩石进行分类预测，并与实测结果进行比较。研究结果表明：利用岩石可爆性分级的未确知均值分级模型所得预测结果与实测结果相吻合，准确率达100%为岩石可爆性分级提供了一条新的途径。

岩石可爆性；分级；未确知均值分级方法

岩体可爆性是指在炸药爆炸的作用下岩石或岩体发生破坏的难易程度，是岩体的工程地质条件和岩体物理力学性质的综合体现。岩体可爆性分级可为合理爆破参数设计提供指导，大大提高铲运、运输和破碎效率，减少二次破碎工作量。由于岩体的复杂性和多样性、爆破过程的瞬时性和复杂性，目前国内外就岩体可爆性评价方法未达成共识，评价指标也存在较大分歧，有的用炸药消耗量[1]，有的用爆破效果[2]，但大部分学者倾向于用多种指标来建立分级评判方法，如加权聚类分析方法[3−4]、模糊综合评判法[5]、熵权属性识别法[6]、蚁群算法[7]、神经网络模型[8]等。评判方法有多种，但如何合理地确定指标的权重，目前主要有列表法、打分法、层次分析法等，虽然这些方法简单易操作，但容易受主观因素等不确定影响，会影响分析的准确性。如何将不确定信息考虑在内并进行分级有待研究。刘开第等[9−11]建立了未确知理论，并给出了未确知测度评价模型，在城市环境质量评价、膨胀土分类评价、尾矿库溃坝风险评价中取得了较好的效果。在此，本文作者借鉴未确知理论的思想来确定指标权重并建立模型，以便为岩体可爆性分级提供一条新途径。

1 未确知均值分级方法计算理论

1.1 确定待测事物的分类模式系统

设1，2，…，R为待分类的个对象，则分类对象空间={1，2，…，R}。对R∈(≤)，有个评价指标1，2，…，x，则评价指标空间为={1，2，…，x}，于是，可表示为维向量(其中，为研究对象关于测量指标的测量值)。对每个有个分类等级1，2，C，分类空间记为，={1，2，C}。设C表示分类等级，则级高于1级，记为1＞2＞…＞C，若{1，2，…，C}满足1＞2＞…＞C或1＜2＜…＜C，则称C属于是分类对象空间={1，2，…，R}的1个有序分割类。假设某个分类样本集有个样本C类，则第个分类等级中各样本的评价指标可表示为，求其平均值，可知分类样本集的分类中心[12−15]。

1.2 单指标测度

其中：=1，2，…，；=1，2，…，；=1，2，…，。则称为未确知测度，简称测度[14, 16]。称矩阵

为单指标测度分类矩阵(其中：=1，2，…，)。

1.3 指标权重的确定

用w表示测量指标x与其他指标相比具有的相对重要程度，要求w满足0≤w≤1，且，称w为x的权重，{1，2，…，w}称为指标权重向 量[13−14]。

令

则w体现x的重要程度，且0≤w≤1，，故w可作为x的权重。

1.4 多指标综合测度评价向量

由于0≤≤1，并且

所以，为未确知测度[14−16]。称(μ1，μ2，…，μ)为样本R的多指标加权综合测度分类向量。

1.5 置信度识别准则

若1＜2＜…＜C，引入置信度识别准则如下：设为置信度(常取0.6或0.7)，1＜2＜…＜C，令

则认为分类对象R属于第0个评价类[12]。

2 岩体可爆性分级的未确知均值分级分析模型

2.1 评判指标的选择

影响岩体可爆性的因素多达十几个，其中包括岩石物理力学性质、岩体完整性系数、炸药性能、岩体动力学性质等。这其中许多因素存在较高的相关性。若选取相关性较高的2个参数来衡量可爆性，则岩石的可爆性将降低。文献[17]研究了采用岩石有关指标使可爆性更加合理和有效的方法，表明单轴抗压强度与单轴抗拉强度存在相关性，因此，本文选取抗拉强度作为评价指标；岩石容重反映岩石爆破过程中块度位移消耗的能量，有必要作为指标；岩体完整性系数反映岩体中裂隙的发育程度，裂隙越发育，爆破消耗的能量越少，因此，是必不可少的评价指标；而岩石动力特性与岩石的抗压或抗拉强度有较高的相关性，前面已经选取了岩石抗拉强度，则岩石动力特性可以忽略不计。综上所述，以岩石容重(1)、岩石抗拉强度(2)、岩石完整性系数(3)作为岩石可爆性分级的评判指标。

2.2 分类判别指标的未确知测度函数

以文献[17]所提供的14种岩石为例进行样本数据训练，见表1。并以岩石容重、抗拉强度、岩石完整性系数作为未确知均值分级分析模型的评判指标，评判集为(1，2，3，4，5) (其中：1为易爆岩石评判指标(Ⅱ)，2为较易爆岩石评判指标(Ⅲ)，3为中等爆岩石评判指标(Ⅳ)，4为较难爆岩石评判指标(Ⅴ)，5为难爆岩石评判指标(Ⅵ))。用表1中的数据建立未确知测度函数，求得各分级样本指标的平均值，分别用，和表示，其结果见表2。根据表2所示结果建立各指标的测度函数，见图1~3。为了考察岩石可爆性分级分析模型的准确性和有效性，用分析模型对14种岩石实测评判指标进行检验，检验结果与实测结果相吻合，表明所建立的模型是可靠的。

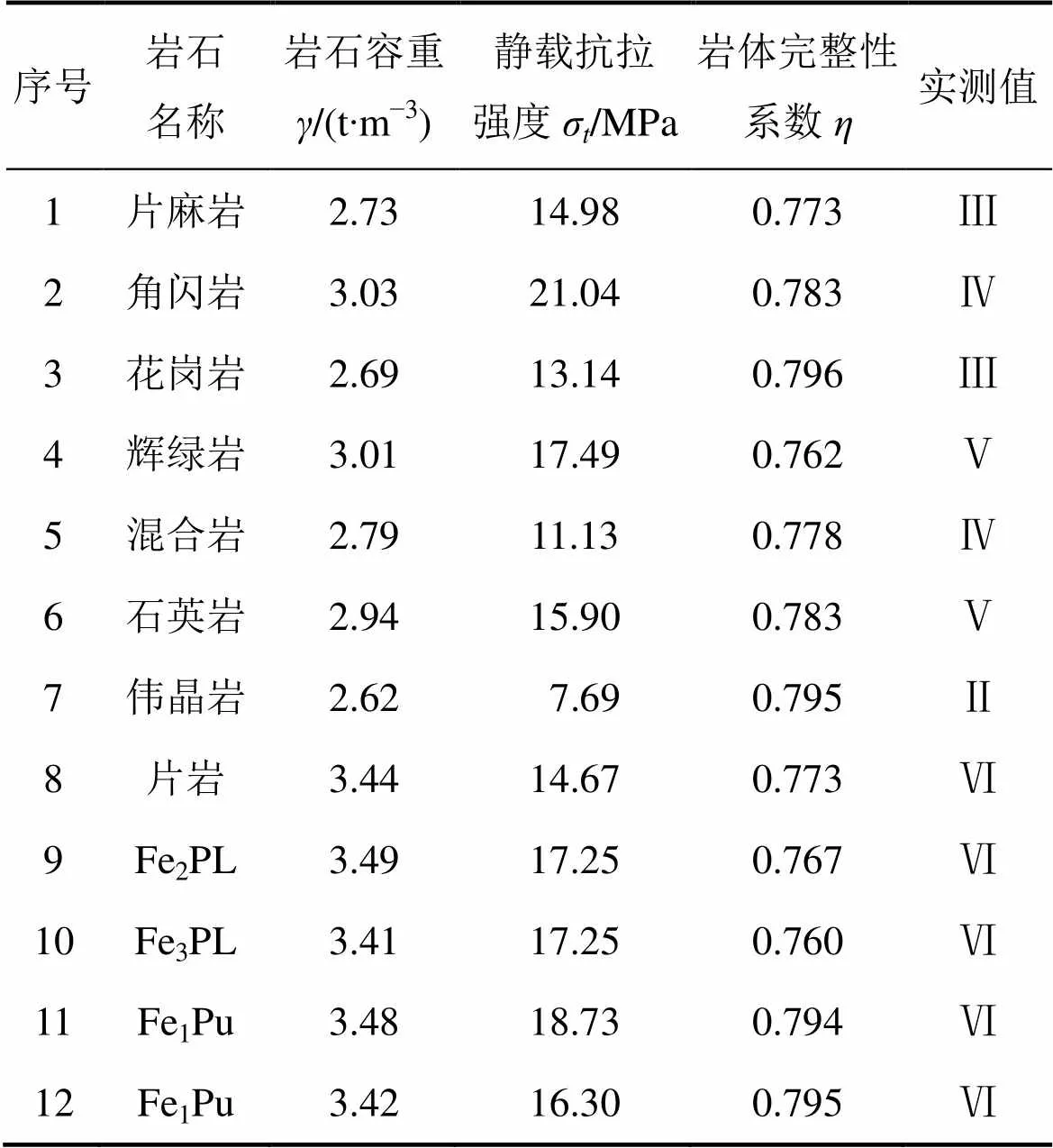
表1 岩石样本实测参数

表2 样本分类数据

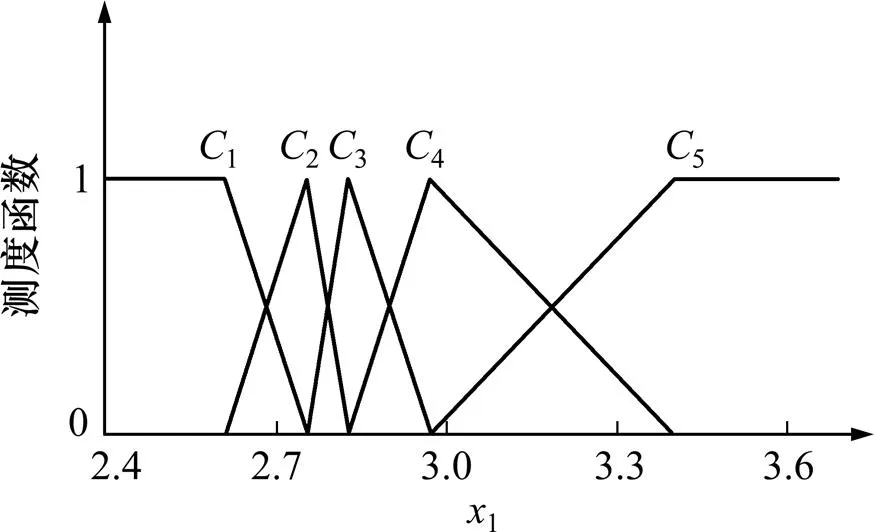
图1 岩石容重的未确知测度函数

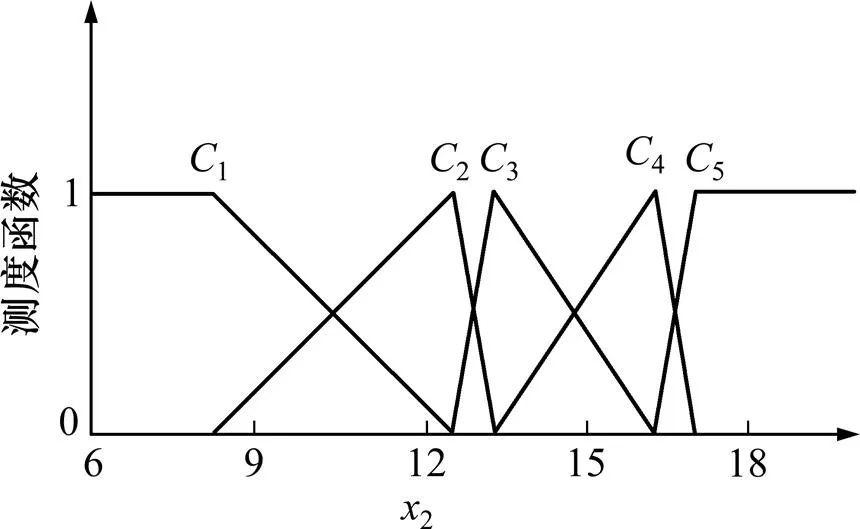
图2 岩石抗拉强度的未确知测度函数

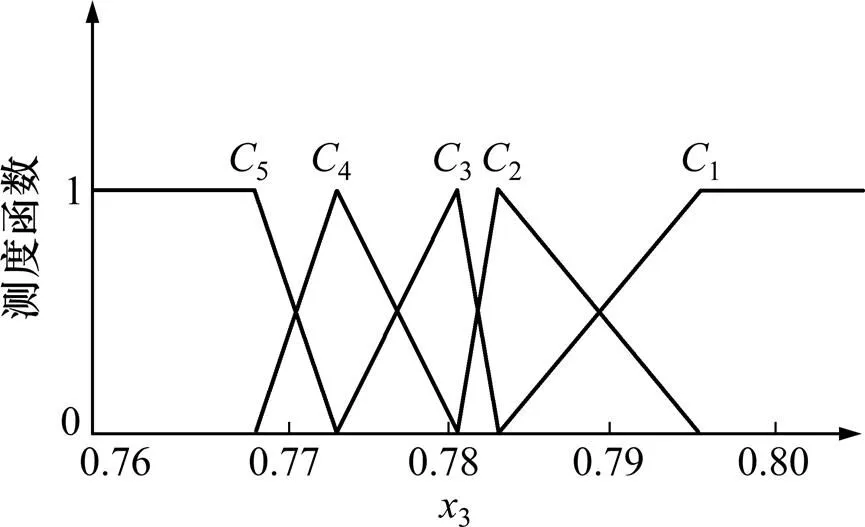
图3 岩石完整性系数的未确知测度函数

3 工程实例应用

沙坝矿区采用中深孔爆破。由于爆破块度不合适，需要对爆破参数进行优化，因此，有必要对岩石可爆性分级进行研究，以便为爆破参数优化提供依据。将本文所建立的模型应用到矿区4种岩石中，依次为白云岩、磷块岩、砂岩及页岩。4种岩石的容重、抗拉强度、完整性系数的实测值见表3。

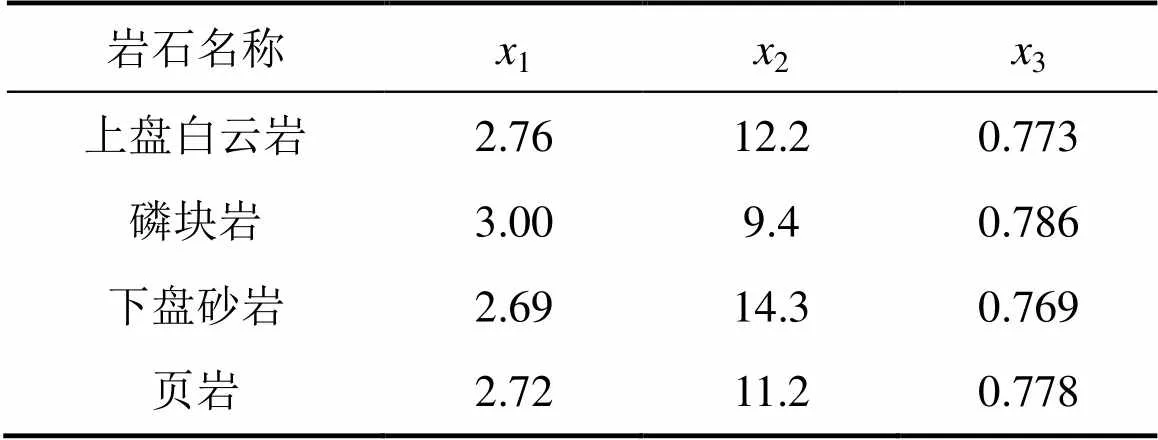
表3 矿区4种岩石可爆性评判指标实测值

以上盘白云岩为例，根据表3和图1~3所示未确知测度函数，可求得单指标测度评价矩阵：

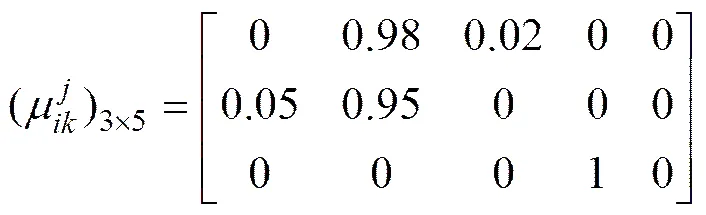
取置信度=0.6，由多指标综合测度评价向量和置信度识别准则式(9)可以判定上盘白云岩可爆性分级为4，与实测结果相吻合。同理可得到其他3种岩石的分级情况，评价结果见表4。表4同时列出了神经网络法[8]和熵权属性识别法[6]评价结果。评价结果与实测结果相吻合，准确率达100%，而由其他2方法所得结果与实际测量结果有些不同。由此可见：将未确知均值分级方法应用到岩体可爆性分级中是可靠的。

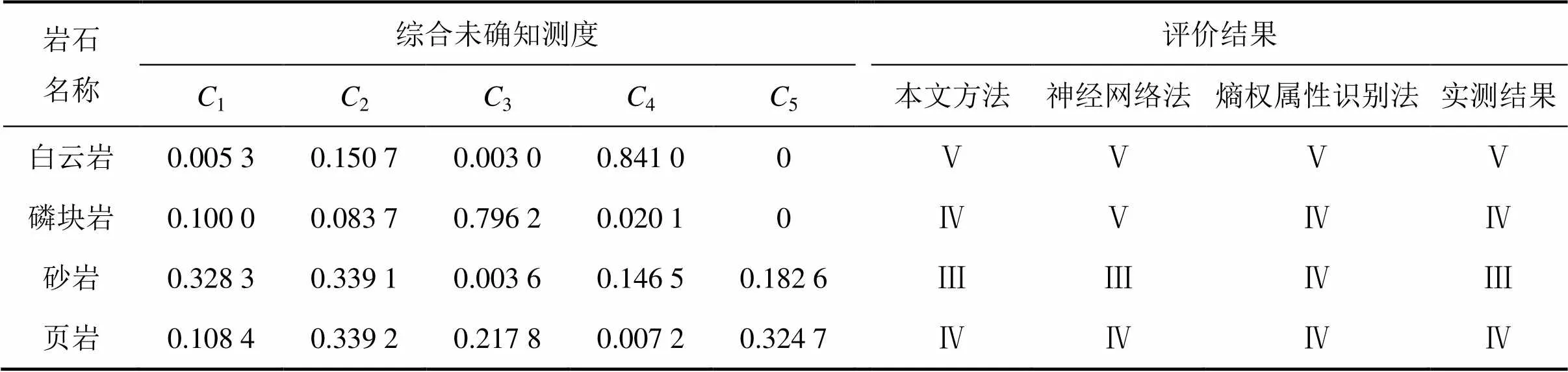
表4 岩石可爆性未确知均值分级法评价结果

4 结论

1) 综合考虑岩石的物理力学性质和岩体的结构特性，引入未确知均值分级理论，建立了岩石可爆性分级分析模型。

2) 将该模型选用岩石的容重、抗拉强度及岩石的完整性系数作为评判指标，并利用实测数据建立测度函数。且在分类过程中，由信息熵理论确定各指标的权重，避免了主观因素的影响，而且对模型进行了验证，比较真实地反映了岩体可爆性分级的情况。岩石可爆性分类的未确知均值分级分析模型的准确率为100%，为岩石可爆性分级提供了一条途径。

[1] 葛树高. 矿岩可爆性评价与合理炸药单耗的确定[J]. 有色金属, 1995, 2(3): 21−24. GE Shugao. Estimation of rock blastibility and determination of adaptive explosive consumption[J]. Nonferrous Metals, 1995, 2(3): 21−24.

[2] 钮强. 我国岩石爆破性分级的试验研究[J]. 金属矿山, 1984, 12(1): 2−8. NIU Qiang. The study of classification of rock blastability in our country[J]. Metal Mine, 1984, 12(1): 2−8.

[3] 璩世杰, 毛市龙, 吕文生, 等. 一种基于加权聚类分析的岩体可爆性分级方法[J]. 北京科技大学学报, 2006, 28(4): 324−329. QU Shijie, MAO Shilong, LÜ Wensheng, et al. A method for rock-mass blastability classification based on weighted clustering analysis[J]. Journal of University of Science and Technology Beijing, 2006, 28(4): 324−329.

[4] 李永强, 张杰, 许利生, 等. 岩体可爆性分级数学模型及其应用[J]. 金属矿山, 2008, 15(11): 36−38. LI Yongqiang, ZHANG Je, XU Lisheng, et al. Mathematical model for rock blastability classification and its application[J]. Metal Mine, 2008, 15(11): 36−38.

[5] 张德明, 王新明, 郑晶晶, 等. 基于模糊综合评判的矿岩体可爆性分级[J]. 爆破, 2010, 27(4): 43−48. ZHANG Deming, WANG Xinmin, ZHENG Jingjing, et al. Blastability classification of rock and mine based on fuzzy comprehensive evaluation[J]. Blasting, 2010, 27(4): 43−48.

[6] 李蓉, 宋娟, 何永延. 基于属性识别理论的岩体可爆性分级方法[J]. 金属矿山, 2008, 5(9): 32−34. LI Rong, SONG Juan, HE Yongyan. Classification for rockmass blastability based on attribute recognition theory[J]. Metal Mine, 2008, 5(9): 32−34.

[7] 方崇, 成艳荣, 代志宏. 基于蚁群算法岩体可爆性分级的投影寻踪回归方法[J]. 工程爆破, 2010, 16(1): 12−16. FANG Chong, CHENG Yanrong, DAI Zhihong. Blastability classification method of projection pursuit evaluation based on an ant colony algorithm in underground rock[J]. Engineering Blasting, 2010, 16(1): 12−16.

[8] 冯夏庭. 岩石可爆性神经网络研究[J]. 爆炸与冲击, 1994, 4(2): 5−13. FNEG Xiating. A study on neural network on rock blastability[J]. Explosion and Shock Waves, 1994, 4(2): 5−13.

[9] 刘开第, 庞彦军, 孙光勇, 等. 城市环境质量的未确知测度评价[J]. 系统工程理论与实践, 1999, 19(12): 52−58. LIU Kaidi, PANG Yanjun, SUN Guangyong, et al. The unascertained measurement evaluation on a city’s environmental quality[J]. Systems Engineering Theory & Practice, 1999, 19(12): 52−54.

[10] 董陇军, 李夕兵, 宫凤强. 膨胀土胀缩等级分类的未确知均值聚类方法及应用[J]. 中南大学学报(自然科学版), 2008, 39(5): 1075−1081. DONG Longjun, LI Xibing, GONG Fengqiang. Unascertained average clustering method for classification of grade of shrink and expansion for expansive soils and its application[J]. Journal of Central South University (Science and Technology), 2008, 39(5): 1075−1081.

[11] 彭康, 李夕兵, 王世鸣, 等. 基于未确知测度模型的尾矿库溃坝风险评价[J]. 中南大学学报(自然科学版), 2012, 43(4): 1447−1453. PENG Kang, LI Xibing, WANG Shiming, et al. Optimization model of Unascertained measurement for dam-break risk evalution in tailings dams[J]. Journal of Central South University (Science and Technology), 2012, 43(4): 1447−1453.

[12] 万玉成. 未确知在预测与决策问题中的应用[D]. 南京: 东南大学经济管理学院, 2004: 22−27. WAN Yucheng. Sduty on the application of unascertained in forecasting and decision making[D]. Shool of Economics and Management. Southeast University, 2004: 22−27.

[13] 曹庆奎, 刘开展, 张博文. 用熵计算客观型指标权重的方法[J]. 河北建筑科技学院学报, 2000, 17(3): 40−42. CAO Qingkui, LIU Kaizhan, ZHANG Bowen. Calculation method of objective index weight by entropy[J]. Journal of Hebei Institute of Architectural Science and Technology, 2000, 17(3): 40−42.

[14] 董陇军, 李夕兵, 宫风强. 开采地面沉陷预测的未确知聚类预测模型[J]. 中国地质灾害与防治学报, 2008, 19(2): 95−99. DONG Longjun, LI Xibing, GONG Fengqiang. Predicting surface subsidence induced by mining based on unascertained clustering method[J]. The Chinese Journal of Geological Hazard and Control, 2008, 19(2): 95−99.

[15] 董陇军, 王飞跃. 基于未确知测度的边坡地震稳定性综合评价[J]. 中国地质灾害与防治学报, 2007, 18(4): 74−78. DONG Longjun, WANG Feiyue. Comprehensive evaluation on seismic stability of slopes based on unascertained measurement[J]. The Chinese Journal of Geological Hazard and Control, 2007, 18(4): 74−78.

[16] 宫风强, 李夕兵, 董陇军. 基于未确知测度理论的采空区危险评价研究[J]. 岩石力学与工程学报, 2008, 27(2): 323−330. GONG Fengqiang, LI Xibing, DONG Longjun. Underground goaf risk evaluation based on uncertainty measurement theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 323−330.

[17] 璩世杰, 辛明印, 毛市龙, 等. 岩体可爆性指标的相关性分析[J]. 岩石力学与工程学报, 2005, 24(3): 468−474. QU Shijie, XIN Mingyin, MAO Shilong, et al. Correlation analyses of blastbility indexes for rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(3): 468−474.

(编辑 陈灿华)

Unascertained average clustering for classification of rock mass blastability and its application

DAI Bing, ZHAO Guoyan, DONG Longjun

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

The unascertained measurement theory was used to classify the rock mass blastability, and the unascertained average clustering model for classifying blastability of rock mass was established, including three indexes reflecting the blastability of rock mass, i.e., density, tensile strength and intactness coefficient of rock mass. The indexes function of unascertained measure of 14 sets of rock mass samples was established,the indexes were calculated by entropy weight theory, and the prediction for the classification of rock mass blastability was carried out using the rules of credible recognition. Classification of the four rock masses in mining area was predicted using unascertained average clustering model and compared with the actually measured values, and the accurate rate was 100%. The results show that the predicted classification is consistent with the actual measured result, which provides a new way to classify the rock mass blastability.

rock mass blastability; classification; unascertained average clustering model

10.11817/j.issn.1672-7207.2015.06.025

TD315

A

1672−7207(2015)06−2157−05

2014−07−12；

2014−09−27

国家重点基础研究发展计划(973计划)项目(2007CB209402)；国家自然科学基金资助项目(面上项目)(51324744)(Project (2007CB209402) supported by the National Basic Research Development Program (973 Program) of China; Project (51324744) supported by the National Natural Science Foundation of China (General Program))

赵国彦，博士，教授，从事采矿工程、矿山安全和岩石力学与工程方面的教学与研究工作；E-mail：522480124@qq.com