球面渐开线齿面的形成理论及其NURBS精确拟合方法

丁撼，阿达依·谢尔亚孜旦



球面渐开线齿面的形成理论及其NURBS精确拟合方法

丁撼，阿达依·谢尔亚孜旦

(新疆大学机械工程学院，新疆乌鲁木齐，830046)

区别于螺旋锥齿轮研究领域一直占据主导地位的局部共轭原理及其所设计和加工出来的近似球面渐开线齿形，基于近些年相关球面渐开线的研究成果的探讨，改进球面渐开线齿面形成理论，并对关键的产形线方程做推导。另外，利用球面渐开线齿面形成理论快速精确地求解边界曲线和齿廓曲线族，并结合三次NURBS曲线曲面造型技术的在CAD/CAM中的优势完成球面渐开线齿面的精确拟合。最后，在利用蒙皮法构造的NURBS齿面基础上提出相关优化方案，完成齿面数据的参数化和曲面的精确拟合，以进一步提高齿面精度，并为齿面接触分析提供齿面数据和基础模型。

螺旋锥齿轮；球面渐开线；产形线；齿廓曲线族；三次NURBS; 蒙皮法

螺旋锥齿轮是现代机械工业中不可替代的相交轴间的动力传动部件[1]。一直以来，以Gleason公司为代表的配备有先进制造专家系统(GEMS)的Free-From型全功能数控铣齿机床代表着加工技术的最新最高水平[2]。其近似球面渐开线齿形的设计与加工研究也一直在螺旋锥齿轮研究领域占据着主导地位。而球面渐开线理论在螺旋锥齿轮设计与加工中的研究却起步较晚，其中以我国的吉林大学的科研团队最为突出，研究并创建了以球面渐开线理论为基础的“产形线切齿法”这一新的加工方法，并获得了发明专利[3]和研究成果[4]。另外，国外的Suh[5]和Dacak[6]也进行了球面渐开线在锥齿轮建模方面的研究。但是，对于球面渐开线理论在螺旋锥齿轮方面的基础理论研究尤其是球面渐开线齿面形成理论的相关细节和重要结论还存在一些不足与缺陷，有待进一步完善和求证。另外，非均匀有理B样条(NURBS)广泛应用于汽车、宇航、船舶、机械、模具等行业的CAD/CAM系统中，成为几何造型强有力的工具。而且国际标准组织颁布的STEP标准中，NURBS方法是定义产品形状的主导数学方 法[7]。本文作者立足于前人已取得的成果，改进了球面渐开线齿面形成理论，并对其关键环节作了推导和论述。同时借助三次NURBS造型技术在CAD/CAM中的强大功能和优势[8]，对球面渐开线齿面形成理论在螺旋锥齿轮快速精准自由造型设计方面作了相关的研究，提出了相关的方法和思路，以此为更加多元化的螺旋锥齿轮设计与加工创造条件。

1 球面渐开线原理应用的探讨

1.1 球面渐开线原理

当平面在基圆锥上滚动时，平面上的任一点的运动轨迹就称为球面渐开线，该圆锥为基圆锥。如图1所示，圆平面与基圆锥01相切并在锥面上作纯滚动，圆平面上的一动点在空间的运动轨迹就是一条渐开线。由于动点在渐开线上任意位置到基圆锥顶点的距离始终相等，故该渐开线是在以点为球心的球面上。当圆平面由初始0位置滚动到位置时，动点的运动轨迹为球面渐开线00。根据球面三角学和边角关系以上推导，则球面渐开线方程可由其线上的任意一点的球面偏角为[9]：

根据如图球面坐标系，可以简化为：

式中：，和分别为球面坐标系中对应的坐标轴；δ为球面渐开线上某点所对应的锥角，b为基圆锥角。

图1 球面渐开线原理

1.2 有关应用的探讨

吉林大学开创性地提出的“形线切齿法”可以简单转化描述为；依照球面渐开线原理，当一圆面与一基锥面相切并在其上纯滚动时，圆面上的点可构成球面渐开线，而由这些连续的点所组成的线则可构成球面渐开线齿面。如图2所示，曲线段0K在空间的运动轨迹就形成了轮齿的齿面。圆面称为发生面，曲线0称为发生线，而曲线0K则称为产形线。其中，产形线为发生圆面上的一条非切线的曲线，如果以该产形线为刀刃，通过一定装置控制处于基圆锥位置的工件齿坯和刀刃的相对运动，完成其空间轨迹的加工运动，就可切出螺旋锥齿轮球面渐开线齿形。

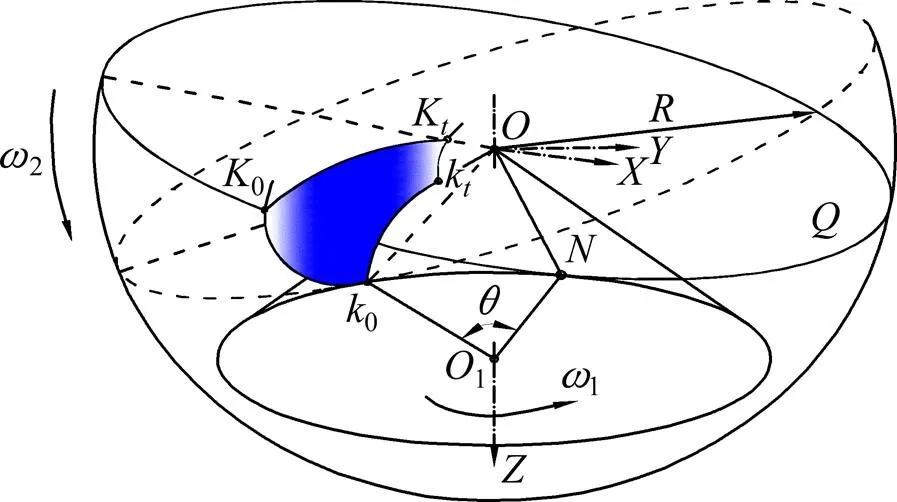
图2 产形线切齿法

但是，该研究团队没有对球面渐开线齿面形成理论做详细的推导和求证，而在加工方法的实验应用和机床研制方面进行大量研究。其实，该加工方法所依据的如上描述的球面渐开线齿面形成理论也存在一定的误差和缺陷：

1) 球面渐开线原理的重要前提就是平面与锥面作纯滚动，则二者的唯一相交线有且只有锥面的母线。

但“产形线切齿法”中，虽然能够控制平面与锥面的相对运动，但不能使产线既在基锥面上又在圆平面上。这样就是得该切齿方法在切出的齿形存在误差或者误差无法有效修正。

2) 刀刃的具体形状即产形线的方程表达式没有做详细且严格的推导。只是作了大小轮产形线的代用求导，且大轮所用的产形线却是直线。而当产形线是直线时，按照正确的齿面形成原理就应该是圆面与基锥面上的唯一相交线即切线上的一小段线段，所形成的却是螺旋直齿轮，其运动轨迹仿真如图3所示。

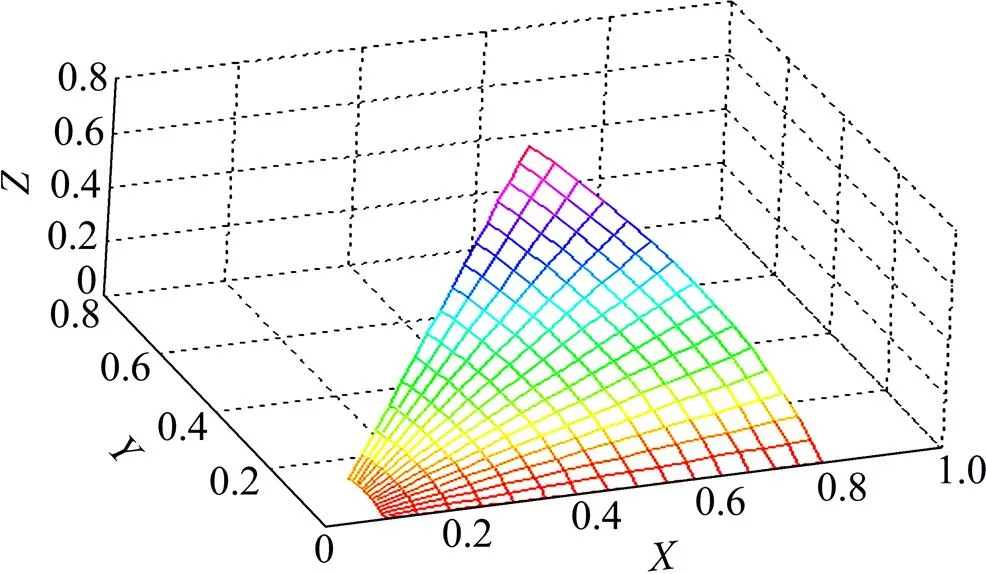
图3 产形线为直线的螺旋直齿面

3) 该球面渐开线齿形能够实现正确的啮合状态即完全共轭状态，但它有一个最大的缺点就是没有可调性，对安装误差很敏感易造成载荷集中于齿面边缘而造成破损现象[10]，相反却没有了“局部共轭理论”[11]的近似球面渐开线齿形的可调性的优势与特点。

4) 该加工方法所依托的实验平台机床的加工性能和加工精度较低，在实际加工过程中的机床和刀具精度，机床噪声和振动、装配及热处理变形所带来的误差却无法进行有效控制。另外，支撑其高精度高质量齿面加工的CAM软件技术却有待完善和提高。

但是，基于球面渐开线理论的球面渐开线齿形还是有其独特的优势和特点，主要为以下2大方面：

1) 在齿面的设计中，能够实现齿面方程的显示表达，快速精准的完成齿面的参数化，并能实现齿轮设计的标准化、模块化、柔性化，能有效提高了齿面主动设计和多元化设计的水平。

2) 避免了以往加工中近似齿形带来的原理性误差，即能到达正确的齿轮啮合状态，且瞬时传动比恒定，减少了齿面接触分析(TCA)所带来的工作量和生产成本。

2 球面渐开线齿面形成理论及推论

2.1 球面渐开线齿面的组成

图4所示为齿面的基本组成。如图4所示，一个完整的齿面应该包括1个顶面、2个侧面、2个端面。顶面为齿顶面，是2条齿顶线与大小端面齿顶圆围成；2个侧面是指轮齿的成对称形状的凹面和凸面，包括工作齿面、齿根面、以及二者之间的过渡圆角曲面3个部分；大小端面是齿廓曲线围成的，一个完整的齿廓曲线有至少包括齿顶圆弧、工作齿廓曲线、过渡圆角、齿根圆弧4个部分。球面渐开线齿面是指由大小端的工作齿廓曲线和齿顶线及过渡圆角线围成的工作齿面。

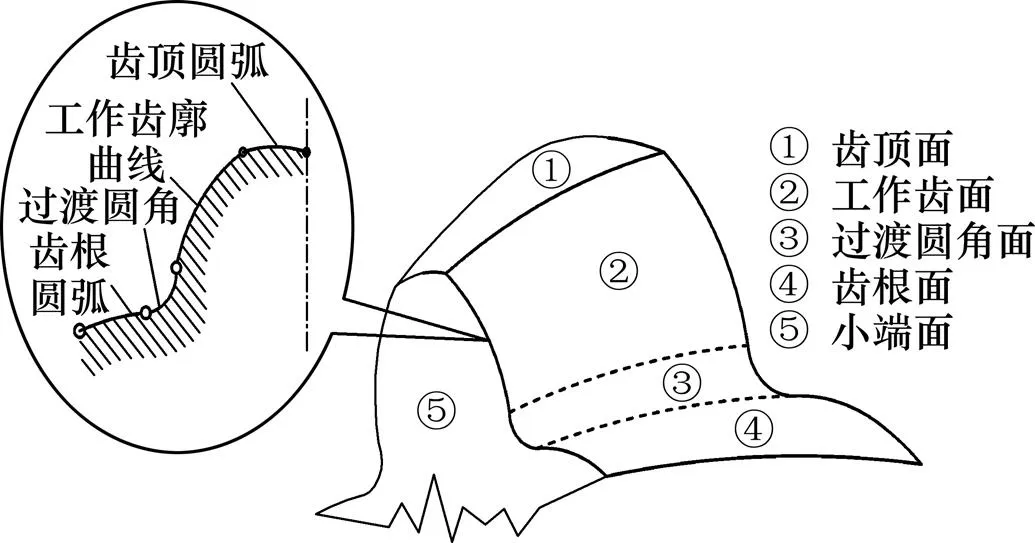
图4 齿面的基本组成

2.2 球面渐开线齿面的形成理论的提出

在螺旋锥齿轮副传动过程中，轮齿上各点到节锥顶点距离始终是不变的，故理论上齿廓为球面曲 线[12]。因此，螺旋锥齿轮球面渐开线原理可以这样论述：球面渐开线齿面由齿廓曲线从一端面向另一端面包络而成。如图5所示，在基锥面上的产形线上取等分点k(=0，1，…，)，当大端面点k=0每旋转则完成一次齿廓曲线的轨迹运动后，直线段0为作纯滚动时的切线就自动转过一定的角度，以下一点k=1再次作空间球面渐开线运动形成一条齿廓曲线，诸如此类，直至产形线起点0向末点k取点时分别完成一次空间运动，则所有轨迹曲线构成了整侧齿面。同时也可以描述为：每改变一次圆面半径即切线转到一定角度θ，切线端点就完成一次空间运动，直至其切线由一端面转向另一端面即切线端点k(=0，1，…，)形成的所有轨迹曲线就可构成球面渐开线齿面。

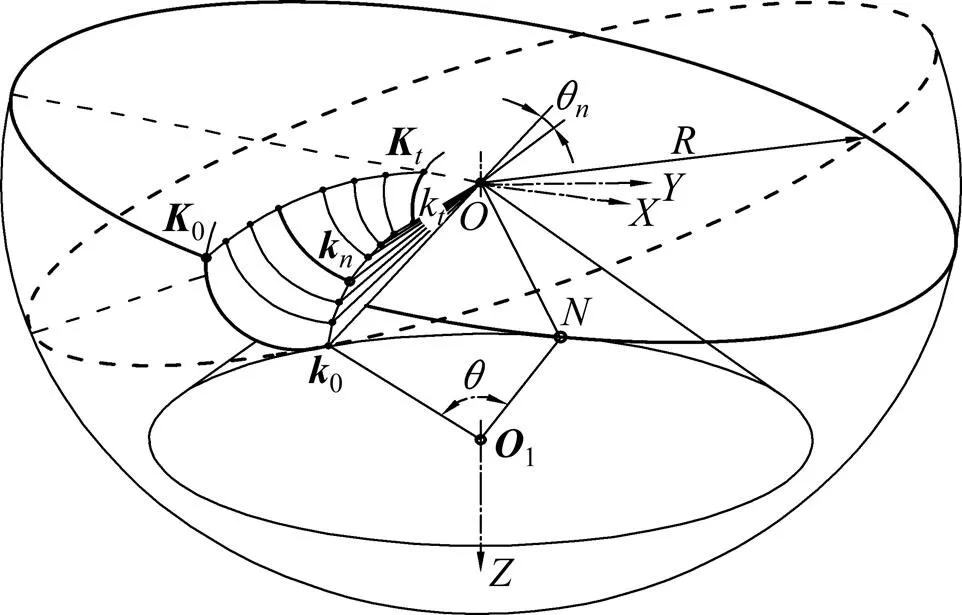
图5 球面渐开线齿面的形成

2.3 产形线方程的求解

由球面渐开线齿面形成理论可知，产形线0k是形成齿面的关键。根据螺旋锥齿轮齿面特征,基锥面上的产形线可以用基圆锥螺旋曲线表示。该螺旋曲线是一条阿基米德螺旋曲线即等螺距螺旋线。如图6所示，根据螺旋线的定义,假设动点k到点的锥距为R，则螺旋线可以用方程表示为：

另有

式中：0和R分别表示基圆锥面上齿轮小端和大端到顶点的距离。

螺旋转角θ的取值可由以下公式求取：

式中：r为切齿刀盘半径，R为名义螺旋角处所对应的锥距。

3 齿面的三次NURBS拟合

3.1 三次NURBS曲面的表达式

三次NURBS曲面为：

式中：，Î[0，1]，为控制顶点，为权因子，向的节点矢量分别表示为：

=[0，0，0，0，4，…，u，1，1，1，1]Î[0，1](8)

同理，向的节点矢量表示一致。,3()和,3()分别为沿向和向的三次B样条基函数，可由以下递推公式求解：

3.2 齿面的三次NURBS拟合

基于三次NURBS曲面造型技术采用蒙面法，通过提取齿面边界和内部截面线族构造齿面。主要的步骤有：

Step 1：构造内部截面线族。如图7所示，首先结合求导的产形线方程通过软件绘制其图形。然后在产形线上等分取点，取等份数可按以下公式求取

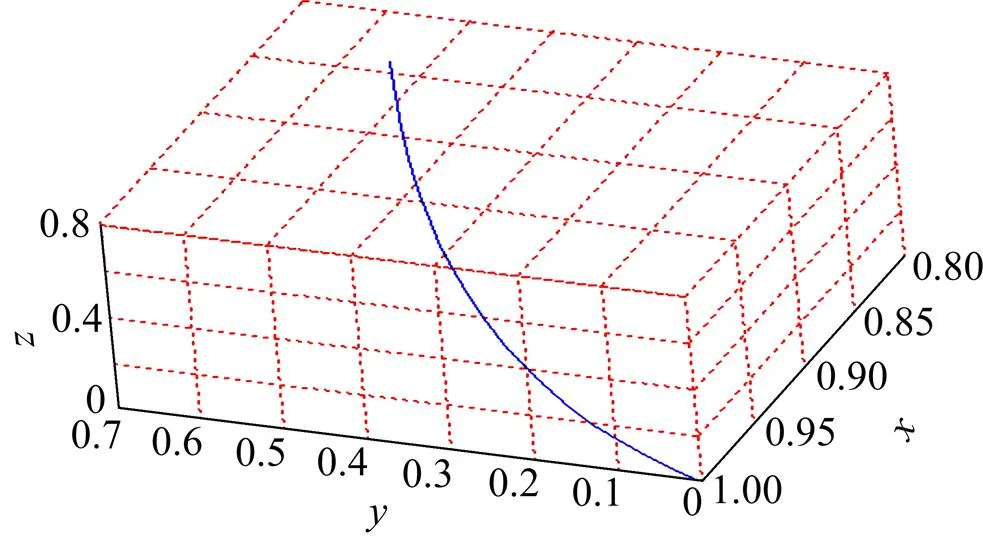
图7 绘制出的产形线

Step 2：确定主要边界曲线。如图8所示，构成球面渐开线齿面的主要边界应是大小端面的工作齿廓(=0)和(=1)、齿顶线(=1)和产形线即过渡圆角线(=0)。其中，向曲线族的起始曲线为(=0)为所求得的产形线，而(=1)可以通过三次NURBS曲线进行拟合，其拟合方法：通过计算机程序模拟出产形线等分点空间运动轨迹所形成的齿廓曲线并输出其另一端点数据信息，记为一组型值点P，由于数据点等分故其权因子h(=0，1，…，)可依次等值选取。一条三次NURBS曲线可以表示为：

式中：节点矢量=[0，1，…，u+3+1]Î[0，1]，(=0，1，…，)为控制点，(=0，1，…，)为权因子，而,3()为三次B样条基函数。

则可利用NURBS曲线插值法反算出符合该条件的NURBS曲线的控制顶点(=0，1，…，)和权因子(=0，1，…，)，完成边界线的拟合。对于反算过程的具体步骤参考文献[9]。

Step 3：求取节点矢量。本文采用一种修正弦长向心积累参数法[13]，求取式(8)所示的节点矢量。

式中：表示向的节点矢量，=1，2，…，。

Step 4：统一各节点矢量。对各个截面曲线的矢量(设为向)做并运算。为了保证形状可采用插入节点的算法，再次求取各截面曲线的控制顶点。

Step 5：求解向控制顶点。根据所求的齿根过渡曲线u线控制点，取统一节点矢量的平均值作为其节点矢量。然后以所求控制点为型值点，逐个反算出向的控制顶点。

Step 6：进行蒙面操作[8]。根据所得的边界曲线和NURBS拟合后的内部截线族，反求得所有的控制顶点后，即可完成NURBS齿面的构造。

4 基于NURBS拟合齿面数据点优化

为了进一步完成整个螺旋锥齿轮齿面的精确拟合，同时为螺旋锥齿轮加工制造中十分关键的齿面接触分析(TCA)和齿面误差修正等技术提供基础模型与数据，本文基于已经完成的球面渐开线NURBS拟合齿面提出了其齿面数据点的优化方案。

4.1 齿面数据点的参数化

在对拟合的基面进行参数化时，通常选取控制点的数据投影点对应的距曲面的最小距离点的参数值作为数据点的参数值。该映射过程中，数据点满足以下公式[14]：

式中：为曲面的雅克比矩阵，为齿面点阵。

上式可采用牛顿迭代法求解：首先将网格划分成等参数曲线网格，得出每一个网格点的坐标值和参数值。然后以距离该数据点最近的网格节点的参数值作为初始值，进行迭代搜索运算，就可完成数据的精确参数化。

4.2 齿面数据点的精确拟合

由于在齿面NURBS拟合中，曲面的控制点数、节点矢量、三次基样条函数都进行了求解。建立NURBS重构基面对原始齿面数据点的集合逼近误差为目标函数的优化模型，以基面的控制顶点为自由度，求解最优解，就可完成最佳曲面逼近。因此，以原始数据点到基面上最近距离作误差逼近优化模型为：

式中：为基面上拟合曲线的数目，为数据点的数目。

该优化模型实质上是一个无约束的二次规划问题，能转化超线性方程组，根据拟合中的精度要求赋予权因子相应的权值后，就可用豪斯荷尔德变换法[14]快速求解。

4.3 算例

本文给出了基于球面渐开线齿面形成理论和NURBS方法的齿面优化后的算例。牛顿迭代的NURBS曲线拟合误差如图9所示，在NURBS精确拟合后的螺旋锥齿轮齿面取点进行牛顿迭代的参数点数值与理论值作比较，通过程序计算得出的牛顿迭代后，齿面误差良好，且非常符合齿面精度要求。图9所示为第5次和第30次迭代后的结果。前者牛顿迭代后的平均齿面拟合误差为0.004 83 mm，后者的误差为0.004 83 mm。齿面NURBS拟合及高斯云图如图10所示，基于球面渐开线齿面形成理论得到齿面进行NURBS重构优化后，并采用齿面插值逼近的方法得出的是12´14的非均匀网格，而且由齿面分析所得出的高斯云图可知：该齿面拟合效果好，光顺性强，能为后续研究提供精确的齿轮模型。

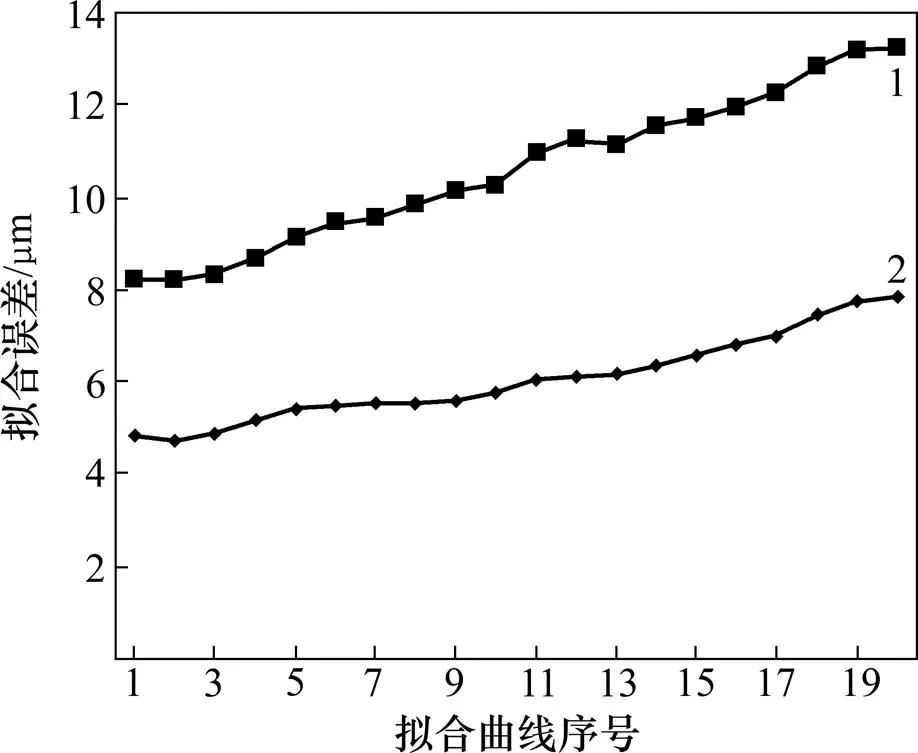
迭代数/次：1—5；2—30

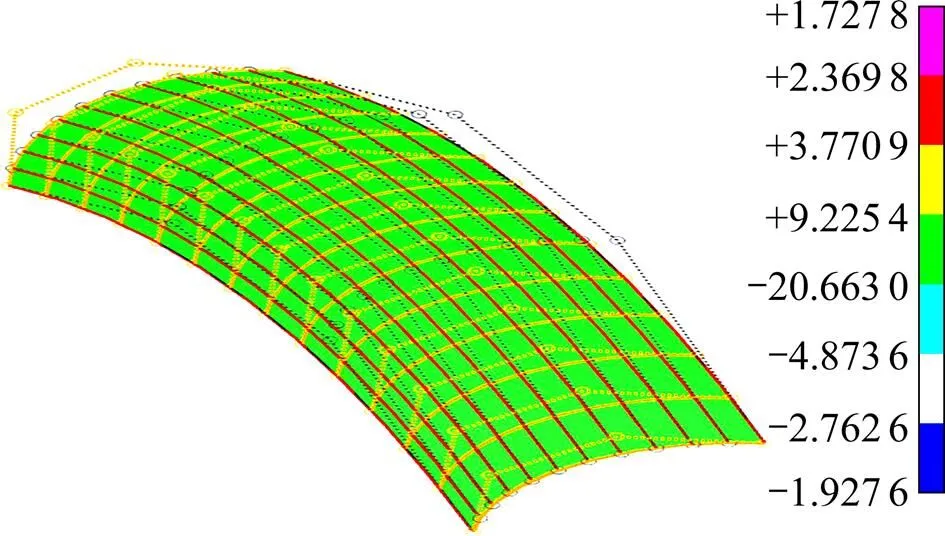
图10 齿面NURBS拟合及高斯云图

5 结论

1) 对球面渐开线理论在螺旋锥齿轮领域的应用作了较为详细的论述，完善并提出了球面渐开线齿面形成理论，能够进行螺旋锥齿轮齿面的快速参数化显示表达。

2) 以NURBS曲线曲面造型技术为基础，对球面渐开线齿面进行了一系列的曲线曲线拟合，为齿面的几何表示提供了统一的标准，并便于为相关绘图和分析软件尤其是齿面接触分析(TCA)提供数据信息和分析模型。

3) 该基于螺旋锥齿轮齿面设计的NURBS方法，可为螺旋锥齿轮的齿面NUEBS加工提供一定的思路和途径，例如对刀具轨迹的计算和规划、对NURBS插补的处理和优化等，可以基于齿面的NURBS设计方法进行拓展和完善。

[1] 李敬财. 螺旋锥齿轮数字化制造基础应用技术的研究[D]. 天津: 天津大学机械工程学院, 2008: 1−10. LI Jingcai. Study on basic applied technology in the process of digitized manufacturing for spiral bevel gear[J]. Tianjin: Tianjin University. School of Mechanical Engineering, 2008: 1−10.

[2] 樊奇, 让·福德. 格里森专家制造系统(GEMS)开创弧齿锥齿轮及准双曲面齿轮数字化制造新纪元[J]. 世界制造技术与装备市场, 2005(4): 87−93. QI Fan, Ron Dafoe. Gleason expert manufacturing system (GEMS) opens a new era for digitized manufacturing of spiral bevel and hypoid gears[J]. World Manufacturing Engineering & Market, 2005(4): 87−93.

[3] 彭福华. 球面渐开线齿形收缩齿制弧齿锥齿轮的切齿方法: 中国, 200610017213.0[P]. 2008−04−02. PENG Fuhua. Cutting method of the spherical involute tooth for the spiral bevel gears on contraction tooth system: China, 200610017213.0[P]. 2008−04−02.

[4] YANG Zhaojun, LI Linan, WANG Yankun, et al. Basic principle and mathematical model of cutting hypoid gears by generating line method[J]. Advanced Materials Research, 2011, 154/155: 113−118.

[5] Suh S H, Jung D H, Lee E S, et al. Modeling, Implementation and manufacturing of spiral bevel gears with crown[J]. Advanced Manufacturing Technology, 2003(21): 775−786.

[6] Dacak M J, Aangeles J. The modeling of bevel gears using the exact spherical involute[J]. J Mech Dcs,1994, 116(2): 364−368.

[7] 宋建民, 席平, 胡毕富, 等. 自由曲面上曲线物理空间和参数空间互相转换算法[J]. 工程图学学报, 2009(1): 97−101. SONG Jianmin, XI Ping, HU Bifu, et al. Quick approach for finding parametric values of 3D points on NURBS surface curves[J]. Journal of Engineering Graphics, 2009(1): 97−101.

[8] 朱心雄. 自由曲线曲面造型技术[M]. 北京: 科学出版社, 2000: 148−165. ZHU Xinxiong. Free modeling techniques of curve and surface[M]. Beijing: The Science Press, 2000: 148−165.

[9] 张鸿源. 圆锥齿轮测量[M]. 北京: 中国计量出版社, 1988: 46−58. ZHANG Hongyuan. Measurement of the bevel gear[M]. Beijing: China Metrology press, 1988: 46−58.

[10] 曾韬. 螺旋锥齿轮设计与加工[M]. 哈尔滨: 哈尔滨工业大学出版社, 1989: 89−162. ZENG Tao. Design and manufacture of spiral bevel gears[M]. Harbin: Harbin Institute of Technology Press, 1989: 89−162.

[11] Litvin F L, Fuentes A, Hayasaka K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears[J]. Mechanism and Machine Theory, 2006, 41(1): 83−118.

[12] 北京齿轮厂. 螺旋锥齿轮[M]. 北京: 科学出版社, 1974: 17−56. Beijing Gear Factory. The spiral bevel gears[M]. Beijing: The Science Press, 1974: 17−56.

[13] 刘相春, 刘文玺, 任慧龙. NURBS改进技术重构复杂船体曲面[J]. 哈尔滨工程大学学报, 2007, 28(11): 1196−1201. LIU Xiangchun, LIU Wenxi, REN Huilong. Defining complex hull surfaces with NURBS[J]. Journal of Harbin Engineering University, 2007, 28(11): 1196−1201.

[14] 孙玉文, 刘宏军, 刘健. 基于NURBS的自由曲面精确拟合方法研究[J]. 机械工程学报, 2005, 40(3): 10−14. SUN Yuwen, LIU Hongjun, LIU Jian. Research on the method of accurate NURBS surface fitting to scattered points[J]. Chinese Journal of Mechanical Engineering, 2004, 40(3): 10−14.

(编辑 陈爱华)

Theory of forming spherical involute tooth surface and its accurate cubic NURBS fitting method

DING Han, ADAYI·Xieeryazidan

(School of Mechanical Engineering, Xinjiang University, Urumqi 830046, China)

Distinguished from the approximate spherical involute tooth profile has been in a dominant position in the research field of spiral bevel gear, and whose design and processing were based on the local conjugate theory, discussing some research outcomes on recent relevant spherical involute, a theory of forming the spherical involute tooth surface was improved, and key part namely the generating line and its equation were detailed by derived. In addition, fast and accurate solutions of the boundary curves and the tooth profile curve families were done by taking advantage of forming principle of spherical involute tooth surface, and based on advantages of modeling techniques of the cubic NURBS curve and surface in CAD/CAM, spherical involute tooth surface precision fitting was completed. At last, related optimization program associated with constructed NURBS tooth surface in the use of the Skinning method was proposed, and the parameterization of tooth surface data and precise fitting surfaces were accomplished, so as to further improve the accuracy of the tooth surface and provide tooth contact analysis for the data of the tooth surfaces and the basic model.

spiral bevel gear; spherical involute; generating line; tooth profile curve families; cubic NURBS; Skinning method

10.11817/j.issn.1672-7207.2015.06.011

TH122

A

1672−7207(2015)06−2052−07

2014−05−13；

2014−07−20

国家自然科学基金资助项目(50965017)( Project (50965017) supported by the National Natural Science Foundation of China)

阿达依·谢尔亚孜旦，博士，教授，从事机械现代设计理论研究；E-mail：adayxj@126.com