基于改进人工蜂群算法的高维多目标优化

王艳娇，肖婧



基于改进人工蜂群算法的高维多目标优化

王艳娇1, 2，肖婧2, 3

(1. 东北电力大学信息工程学院，吉林吉林，132002 2. 哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨，150001 3. 辽宁省交通高等专科学校信息工程系，辽宁沈阳，110122)

为了提高高维多目标优化算法的收敛性和分布性，提出基于改进人工蜂群算法的高维多目标优化算法。首先，利用一种改进的适应值评价方式定量比较高维多目标中个体的优劣；其次，改进人工蜂群算法，使种群迅速收敛于最优的非支配前沿；最后，建立新的分布性维护机制使所获得的非支配解分布均匀、覆盖整个最优前沿。研究结果表明：对于3~8个目标的DTLZ系列测试函数，与PISA算法等几种较流行的高维多目标算法相比，本文方法收敛性好，解集覆盖范围广且分布均匀.

高维多目标优化；人工蜂群算法；适应值评价方式；分布性维护方法

高维多目标优化问题通过协调权衡和折中处理的方法，使不少于3个目标的问题尽可能同时达到最优，是目前世界公认的优化难题和研究热点，其主要研究方向大致可分为以下几个方面：引入新型优化算法或其他机制、提出合适的适应值评价方式及精英选择策略、建立合理的分布性保持机制以及可视化技术。PISA算法(preference rank immune memory clone selection algorithm)[1]，LbsNSGA-II(light beam search based non-dominated sorting genetic algorithm II)[2]和NSGA-II(non-dominated sorting genetic algorithm II)[3]是目前较流行并有代表性的高维多目标算法，但随着目标数的增加，这些算法的优化效果都有所下降，存在计算复杂、所得近似Pareto前沿点不够多、分布不均匀以及覆盖不完整等问题。Karaboga等[4]于2005年提出的人工蜂群算法(artificial bee colony algorithm，ABC)是一种新型群集智能优化算法，该算法操作简单，无需设置很多参数，具有强大的搜索能力，在函数优化问题、人工神经网络训练、滤波器设计、网络优化、机器人路径规划等众多领域应用广泛[5]。文献[6]以NSGA-II算法为基本框架，将人工蜂群算法用于二目标优化问题，收效较好，证实该算法可以解决多目标优化问题，但未涉及高维多目标优化问题。本文作者将这种新型优化算法应用到高维多目标优化中，为此更改人工蜂群算法中跟随蜂的选择方式、侦查蜂的行为，同时根据高维多目标优化问题的特点，提出新的适应值评价方式和新的分布性维护机制，以便实现基于改进人工蜂群算法的高维多目标优化算法，并对3~8个目标的DTLZ2和DTLZ3基准函数进行测试。

1 人工蜂群算法

人工蜂群算法是受蜜蜂采蜜机制启发而提出的一种群智能进化算法，在ABC算法中将蜂群分为引领蜂、跟随蜂和侦察蜂3类，它们在优化过程中所起的作用各不相同。

1) 引领蜂。它的数量为蜜源数量的一半，并总是处于较好一半蜜源的位置上，它们在自身所在蜜源左、右按下式开采新蜜源：

其中：V为新蜜源的位置；x和x分别为蜜源和蜜源(随机选择但不等于)的第维位置；R为[−1，1]间的随机数。

2) 跟随蜂。选择较优蜜源并在其附近按下式搜索新蜜源：

其中：为按轮盘赌方式选择的较优蜜源；为随机选取的不等于的数。通常将引领蜂、跟随蜂所在的位置称为本代蜜源。

3) 侦察蜂。若某一蜜源连续代不变，则启动侦查蜂，随机产生新蜜源代替原蜜源。

ABC算法通过这3种蜜蜂的反复搜索、转换求取最优解，具体过程如下：随机产生一定数量的初始蜜源，将引领蜂置于适应度较优的一半蜜源的位置上，按式(1)搜索产生新蜜源，与对应的初始蜜源比较，若优于初始蜜源，则将新蜜源作为标记蜜源，否则，以初始蜜源作为标记蜜源。跟随蜂按轮盘赌方式挑选较优的标记蜜源并在其附近按式(2)探索新蜜源。将标记蜜源和跟随蜂产生的蜜源作为本代的蜜源，最后判断是否出现侦察蜂，若出现，则随机产生新蜜源代替相应蜜源。

2 高维多目标优化

高维多目标优化算法的最终目标是：使最优解集接近于真实的非支配前沿、覆盖整个前沿区域且分布均匀。传统的二目标优化算法一般都不适合解决高维多目标问题，这是由于迫使二目标优化算法收敛至最优非支配前沿的进化压力为Pareto支配等级的差异，而随着目标维数增大，基于Pareto支配的非支配解急剧增加，种群中大部分解都处于最优排序等级，由于几乎所有解都是平等的，因此，无法选择出较好解，使得原有算法只能收敛至局部最优非支配前沿。

为增大高维多目标优化算法的选择压力，目前主要采取的措施如下。

1) 增加种群数目。这虽然在一定程度上增大了算法的选择压力，但未从本质上改变压力的产生方式，结果有所改善但很难收敛至最优非支配前沿，也大大减低了算法的运行效率。

2) 改进原有的Pareto排序机制，如引入偏好信息的支配，这些方法随着维数的增加，改进效果越来越不明显，不适合处理维数较高的多目标优化问题[7]。

3) 建立新的排序机制，如MSOPS(multiple single objective Pareto sampling)[8]和MSOPS-II(multiple single objective Pareto sampling II)[9]算法，但当目标维数较高时，由于难于设置合适权重或者预先不知道最优结果使得上述的方法受到限制。

4) 将高维多目标优化问题转化为低维问题处理，如主成分分析法[10]和MDMOEA算法(MOEA based on new selection schemes for dealing with many-objective problems)[11]，这是加大选择压力的最有效方式，但极易聚集于某一区域。

MDMOEA算法是解决高维多目标优化问题的新算法，它不同于传统的多目标算法，是以排序等级为第一标准，以多样性测度如拥挤距离为第二标准建立的一种平衡算法的收敛性和分布性的新适应值评价方法，定量比较个体的优劣程度，使其可以较快收敛至最优的非支配前沿，但该算法的解集覆盖性和分布性都较差。本文借鉴并改进该算法的适应值评价方法，实现基于改进人工蜂群算法的高维多目标优化。下面简要介绍MDMOEA算法的适应值评价方法和高维多目标优化的CAO操作(convergence acceleration operator)[12]。

2.1 MDMOEA算法

MDMOEA算法为高维多目标优化问题的求解提供了一种思路，其核心思想是建立了一种以占优(L-optimality)为基础的适应值评价方法(其中，为个体表现好的目标数与表现差的目标数之差)。占优的定义如下。

设解1和2满足：

其中：N+和分别为自然数集合和目标数目，满足 0＜t＜，0＜q＜，0＜s＜，正则化目标值为

f()为在目标上的归一化适应度，为人为设定参数。若

则称1占优于2。

从上述定义可以看出：在个体进行比较时，与要求个体在所有目标上的表现不低于其他个体的Pareto占优相比，条件更宽松，加大了算法的选择压力。

MDMOEA算法给出的适应值评价公式为

其中：R()为个体的L排序值，相当于L占优于解的数目；d()为NSGA-II[3]中个体间的拥挤距离；

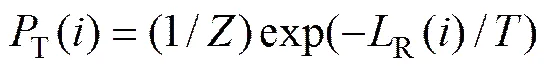
为模拟退火温度。在式(3)中，R()综合考虑了个体在各目标上的优劣，与Pareto排序一样迫使种群靠近最优前沿，而d()依据拥挤距离进行计算，S()依据的是排序值并以模拟退火方式计算所得，增加了种群多样性，平衡了算法的分布性。式(3)综合考虑了收敛性和分布性，决定了算法的进化方向，这与NSGA-II算法中精英种群的作用其实是相同的。但精英种群首先考虑收敛度，其次才考虑分布性，而MDMOEA算法通过退火温度协调收敛性和分布性的重要程度。实验结果证实对于高维多目标问题，这种权衡考虑收敛性和分布性的思想是合理、有效的。

2.2 CAO操作

大多数高维多目标优化算法都只能收敛于局部最优非支配前沿，文献[12]提出一种适用于高维多目标的CAO操作，可以加速算法收敛并在一定程度上避免陷入局部最优。操作步骤如下。

1) 局部搜索改善旧解。设维目标优化问题的一个前沿点为(1，2，…，f)。

①对所有个体在各目标上进行排序，判断个体在各目标上属于边界个体(没有比个体本身更好的位置)还是中间个体，对于边界个体保持不变，对中间个体按下式进行改进：

其中：f,1表示个体1在目标上的函数值；f,2为比个体1更优且与之距离最近的个体2的函数值；为窜改的步长因子。

②自适应调整步长因子。步长因子决定了局部改善解与原解的距离，在一定程度上决定了算法的效率。

设CAO操作的成功率为：s=e/×100%。其中：e为由CAO操作成功引入到下一代进化中的解；为种群数目。当成功率下降到阈值时，通过冷却因子增大为。

2) 从目标空间映射到决策空间。由第1步操作得到可能的改善目标值，由于种群是在决策空间进化，故需将其从目标空间映射到决策空间，这里采用人工神经网络映射方式，具体操作过程如下。

人工神经网络选用径向基网络，将真实未经改善的目标值和相应的决策变量作为神经网络的输入和输出，训练该网络，然后以式(4)的结果作为该网络的输入，利用已训练好的网络求出相应的输出，即为对应的决策变量；若超出范围，则在定义域内随机产生新值，形成新解；若这一新解与相应旧解相比在各目标上都没有退后，则用新解取代旧解。

3 基于人工蜂群算法的高维多目标优化

为更好解决高维多目标优化问题，改进MDMOEA算法的适应值评价方式及人工蜂群算法，使其能够迅速收敛至最优的非劣前沿，并建立新的分布性保持机制。

3.1 适应度评价方式的改进

MDMOEA算法的适应度评价公式中d()和S()是依据NSGA-II算法中的拥挤距离进行计算的，它的作用是避免种群收敛于某一点，使获得的非支配解尽量分布均匀，但该拥挤距离在高维多目标问题中不能很好地评估个体间的密度。与NSGA-II算法中的拥挤距离相比，Harmonic平均距离能够更准确地评价个体间的拥挤程度，会取得更好的优化效果[13]，为此，本文采用Harmonic平均距离，即

其中：通常取2(−1)，为目标数；d为距离个体最近的第个个体的欧式距离。可见，本文提出的改进适应值评价方式仍为式(3)的形式，只是其中d()的计算采用如式(5)所示的Harmonic平均距离。

3.2 人工蜂群算法的改进

将人工蜂群算法与改进适应度评价方式相结合直接用于解决高维多目标问题时容易收敛于局部最优非支配前沿，并且收敛速度不够快，为此进行如下改进。

3.2.1 跟随蜂选择方式的调整

通过多次仿真实验发现，跟随蜂使用轮盘赌方式选择较优蜜源，较贪婪，虽然加快了算法的收敛速度，但降低了种群的多样性也容易早熟收敛。在自由搜索算法[14]中，提出了一个重要模型——灵敏度与信息素配合模型，个体选择某一区域(其灵敏度与信息素能够匹配)进行搜索，步骤如下。

1) 按下式计算个体的信息素()：

其中：()为个体适应度；max和min分别为所有个体的最大和最小适应度。

2) 灵敏度与信息素配合模型。以最小化问题为例，灵敏度与信息素满足下式称为相互配合：

其中：第个个体的灵敏度()为0~1的随机数。与轮盘赌方式类似，本文方法也是从多个符合式(7)的个体中随机选择1个作为。

从这种模型可以看出：每个个体都可以搜索任何区域，这就避免了陷入局部最优；所搜索区域的信息素必须适应其灵敏度，这就使算法有导向作用，决定了算法在搜索空间中的收敛和发散。所以，跟随蜂选择蜜源的方式可以被上述“信息素−灵敏度”配合选择的方式代替，方式如下：按式(6)计算各蜜源的信息素，跟随蜂产生1个灵敏度(0~1的随机数)，选择满足式(7)的蜜源为较优蜜源。

3.2.2 侦察蜂行为的替代

在ABC算法中，侦察蜂的作用是为避免算法陷入局部最优，但由于本文在解决高维多目标优化问题时，1个个体的位置变化会导致所有个体的拥挤距离变化，这样蜜源几乎每代都在变化，很难启动侦察蜂，导致算法易于陷入局部最优。为此，本文设计在跟随蜂产生1个新解后加入强变异操作，代替侦察蜂的行为，起到避免算法陷入局部最优的作用。强变异操作具体公式为

其中：′为随机产生的变异位。若该变异位超出变量定义域范围，则随机产生1点代替该值；若变异后个体在各目标上的表现都不逊于旧个体，则用新个体代替旧个体。这样的个体接收准则只与个体的适应度有关，计算量很少，又可以保证算法的进化方向。

3.3 分布性维护策略

实验结果表明，综合考虑收敛性和多样性建立新的适应值评价公式可以收敛至最优的非支配前沿，但获得的解较集中地聚集于某一区域，分布性较差。而高维多目标优化算法希望解集覆盖广泛、分布均匀，上述方法无法满足这一要求，为此，本文提出后期分布性维护措施。

在二目标优化问题中，精英种群是确保种群进化的原因。进化后期在确保所有个体都处于最优非支配排序的前提下，依拥挤距离可使个体均匀分布。同样地，在高维多目标优化中，可利用拥挤距离使聚集于某一区域的个体分散，但需确保个体处于最优的非支配排序。为此，本文在算法后期建立基于拥挤距离的新型适应值评价标准，具体计算式为

其中：()为个体的适应度；()和X()分别为个体的Harmonic距离及其Pareto支配排序值。依Harmonic距离计算得到的拥挤距离为0~1之间的数，而个体的最优排序等级为1，拥挤距离的作用被充分重视。

在式(9)中，由于Pareto排序越低、Harmonic距离越大的个体越好，可以保证在一直处于最优非支配前沿的前提下，促使种群进化，增大种群多样性，令集中于最优非支配前沿某一区域的种群依Harmonic距离均匀分布于整个的非支配前沿。

3.4 高维多目标人工蜂群算法实现流程

归纳本文提出的高维多目标优化算法，首先采用适应值评价方式将高维多目标优化问题转化为单目标优化问题，改进有强大搜索能力的人工蜂群算法，使种群迅速收敛至最优的非支配前沿；然后，利用分布性维护措施使得聚集于某一区域的解集分散至整个前沿并均匀分布。为了避免混淆，这里称利用前面的适应值评价方式解决高维多目标的过程为第1阶段，分布性维护过程为第2阶段。本文提出的基于人工蜂群算法的高维多目标优化算法的具体操作流程如下。

步骤1 初始化。给出算法相关参数，其中包括种群数目；2个阶段的迭代次数分别为max1和max2；2个阶段计算适应值所需参数和；并随机产生数目为的初始种群。

步骤2 按3.1节方式评价个体。

步骤3 选取适应值较优的/2个个体作为引领蜂的位置，按式(1)搜索产生新个体，若有超出边界的个体，则将其置于边界上。

步骤4 选择引领蜂搜索前后的一半蜜源为本代的初始标记蜜源。

步骤5 跟随蜂按3.2.1节中的方式选择较优个体，按式(2)进行搜索，产生/2个个体。

步骤6 对跟随蜂产生的/2个个体进行强变异操作。

步骤7 将步骤4和步骤6中的个体结合为1个种群。

步骤8 实施CAO操作，得到下一次迭代种群。

步骤9 判断是否达到预设的迭代次数max1，若是则转至下一步；否则，转至步骤2。

步骤10 按式(9)评价种群。

步骤11 执行步骤3~7。

步骤12 判断是否达到预设的迭代次数max2，若是则输出结果，否则，转至步骤10。

3.5 高维多目标人工蜂群算法复杂度分析

为分析本文算法的复杂度，这里给出种群数目和目标数。

算法迭代过程依据适应度评价方式的不同分为2个阶段。以3.1节中的适应度评价方式计算更加复杂，时间复杂度更大，所以，以第1阶段的时间复杂度为算法每代的最坏时间复杂度。算法在步骤3、步骤5和步骤6搜索新蜜源的过程中，其时间复杂度都为(/2)；步骤2和步骤4都需根据提出的改进适应度评价方式评价个体优劣，需计算L排序值和Harmonic距离，其中L排序的时间复杂度与Pareto排序的时间复杂度相当，都为(2)，Harmonic距离的时间复杂度为((2)lg(2)。步骤8中的CAO操作的时间复杂度为()。因此，在每一代的最坏时间复杂度为

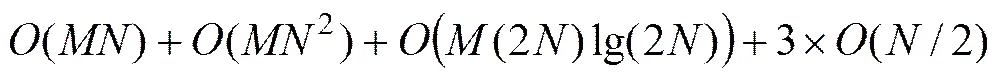
根据复杂度“”的比较关系，上式可以简化为(2)，这表明个体评价的时间复杂度在整个算法的时间复杂度中占主导地位，且本文算法的时间复杂度与现在主流的多目标算法NSGA-II算法的时间复杂度相当。

4 性能仿真和分析

为验证本文算法的有效性和先进性，进行一系列仿真实验，并与目前较优秀的3种算法[1-3]进行比较。实验仿真是在Intel Centrino Duo(CPUT 7250，1G内存、2.0 GHz主频)的计算机上实现，程序采用Matlab7.5语言实现。

4.1 测试函数及性能评价标准

测试函数选用目前常用的可扩展为任意目标维数和自变量维数的DTLZ1，DTLZ2和DTLZ3问题[15]，其中DTLZ1的|x|=7，其最优前沿面为线性超平面，包括11|x|−1个局部最优前沿，一般算法很难收敛于最优非支配前沿，故很难用于判断算法跳出局部最优的能力；DTLZ2的|x|=10，最优前沿为，常用以检测算法的分布效果；DTLZ3的|x|=7，含有3|xk|−1个非支配前沿，函数十分复杂，是DTLZ系列问题中最难的问题，一般算法很难收敛至最优的非支配前沿，故常用此函数评价算法的收敛性。

为评价和对比各算法性能，选取目前国内外常用的收敛性和分布性准则——世代距离GD和间距度量标准S作为性能评价标准[1]。

4.2 实验仿真结果及分析

为充分验证本文方法的有效性，这里进行2部分实验：1) 验证各种改进措施的有效性；2) 验证综合改进后本文方法的有效性.

4.2.1 各种改进措施的有效性

为验证本文提出的基于人工蜂群算法的多目标优化方法各项改进措施的有效性，将本文最终确定的多目标算法与单独改进项的算法进行比较，分别称加入3.1，3.2，3.3节中部分操作的算法为MABC1(improved artificial bee colony algorithm1)，MABC2(improved artificial bee colony algorithm2)和MABC3(improved artificial bee colony algorithm3)算法。此外，为验证本文算法外加的CAO操作的有效性，将本文最终确定的多目标算法与未加入CAO操作的算法MABC4(improved artificial bee colony algorithm4)也进行比较。

各算法参数设置如下：种群数目为200，即引领蜂、跟随蜂数目都为100，第1阶段迭代次数为180次，第2阶段多样性维护的迭代次数为20次，=1，=1 0000。为直观对比改进效果，对3个目标的DTLZ1问题进行测试，随机运行1次，结果如图1所示。

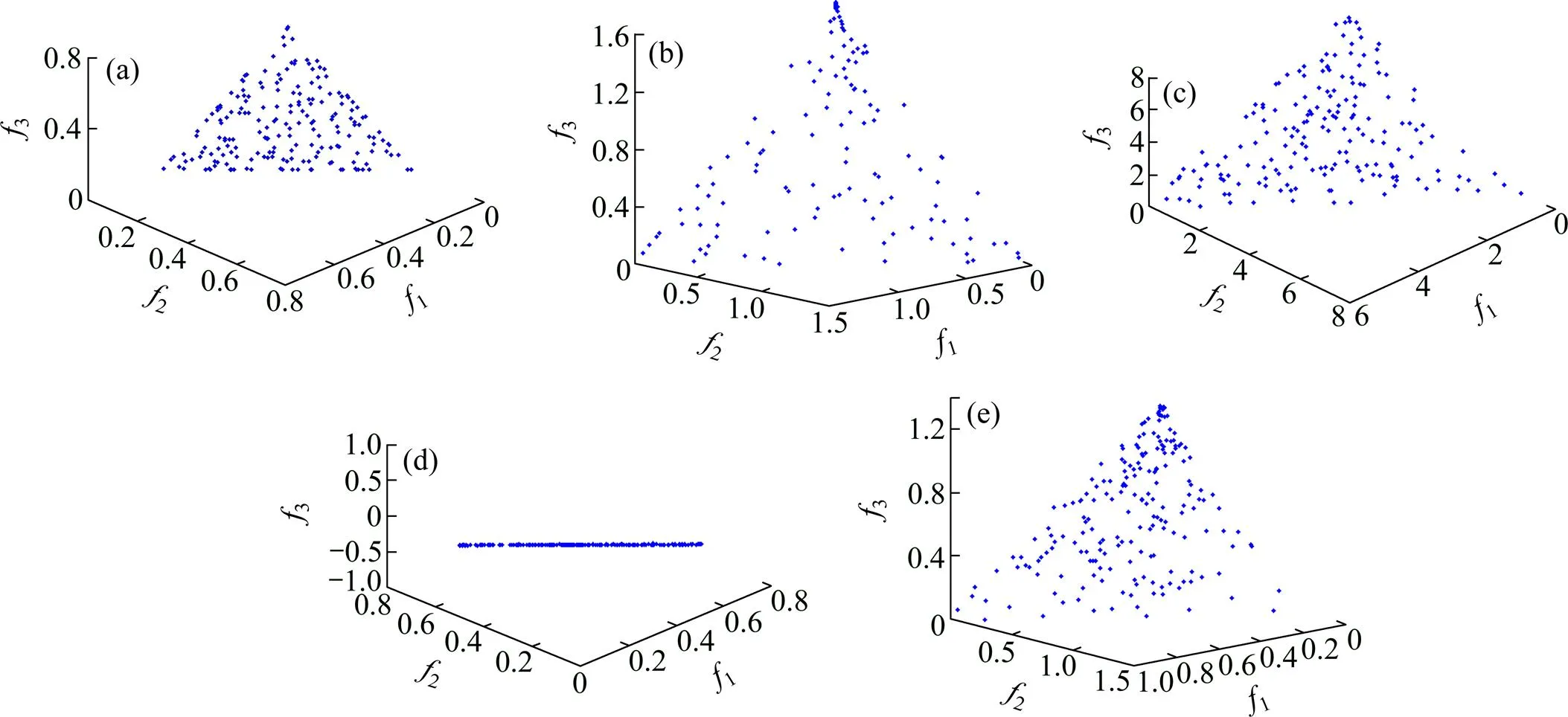
(a) 本文算法；(b) MABC1算法；(c) MABC2算法；(d) MABC3算法；(e) MABC4算法

从图1可以看出：MABC1算法与本文算法相比仅改变了拥挤距离的计算方式，但在规定代数内无法收敛到最优前沿且分布较离散，证明基于改进拥挤距离的适应值评价方式的有效性；MABC2算法在求解具有多个非支配前沿的DTLZ1问题时收敛到局部最优非支配前沿，1+2+3=8，即跟随蜂的新的选择方式和侦察蜂的行为，有利于算法跳出局部最优；MABC3算法可以收敛到最优的非支配前沿，但是聚集于某一区域，即解集覆盖性很差，这证明本文提出的第二阶段的分布性维护措施在种群多样性维护、提高解集覆盖性上优势明显；MABC4算法在固定迭代次数内并未收敛至最优前沿但较接近，说明CAO操作可有效提高收敛速度。

综上证实本文提出的各种改进措施的有效性。

4.2.2 本文方法的有效性

高维多目标优化算法的效果与所选取的优化算法、适应值评价方式及多样性维护措施息息相关，为充分验证本文算法的优势，这里进行如下实验。

实验一：与MDMOEA算法的比较。

本文算法主要借鉴MDMOEA算法处理高维多目标问题的思想，所以，首先将本文算法与文献[11]中的MDMOEA算法进行比较，对5个目标的DTLZ1和DTLZ3问题进行测试。种群数目等参数设置与文献[11]中相同，本文方法保证第二阶段的迭代次数为20次。表1所示为本文算法和MDMOEA算法在各目标上的覆盖范围。

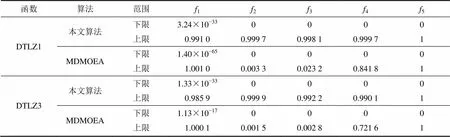
表1 2种算法在各目标上的覆盖范围

实验结果证实：对于上述2个测试问题，这2种方法都可以收敛至最优的非支配前沿；MDMOEA算法的函数评价次数为30 000次，而本文算法的函数评价次数仅为20 000次，即本文算法在收敛速度方面有较大提高，这也就证明对于高维多目标优化问题与遗传算法相比，人工蜂群算法与L支配适应值相结合的方式可使收敛速度显著提高；另外，从表1可以看出：对于上述2个测试函数，MDMOEA算法在第2和第3个目标上的覆盖范围都很小，即其最优非支配解集较集中，而本文算法分布在整个平面空间中，在解集覆盖性上优势明显。

综上所述，经过上述综合改进，与MDMOEA算法相比，在保证收敛效果相当的前提下，本文算法在收敛速度、解集分布性和解集覆盖性上都得到大幅度提高。

实验二：与其他高维多目标算法的比较。

从MDMOEA算法的实验结果可以看出：综合考虑收敛效果和分布效果并不是解决高维多目标问题的最好算法。为表明本文算法的先进性，将本文算法与目前最有代表性的高维多目标算法即PISA算法[1]、LbsNSGA-II[2]和NSGA-II[3]进行对比。为使这4种算法的对比更具科学性，相同参数皆采用文献设置的参数值。本文算法设置的参数来自于多次实验获得的较理想参数值：种群数目为200，即引领蜂、跟随蜂数目都为100；第1阶段迭代次数为480次，第2阶段多样性维护的迭代次数为20次；=1，=10 000。

为了消除随机性对算法评价的不良影响，独立运行10次取平均值，改变目标数目，得到各算法的收敛性和分布性的统计结果，见表2。将本文算法简记为DMABC算法(deal with many objectives based on an improved artificial bee colony algorithm)。

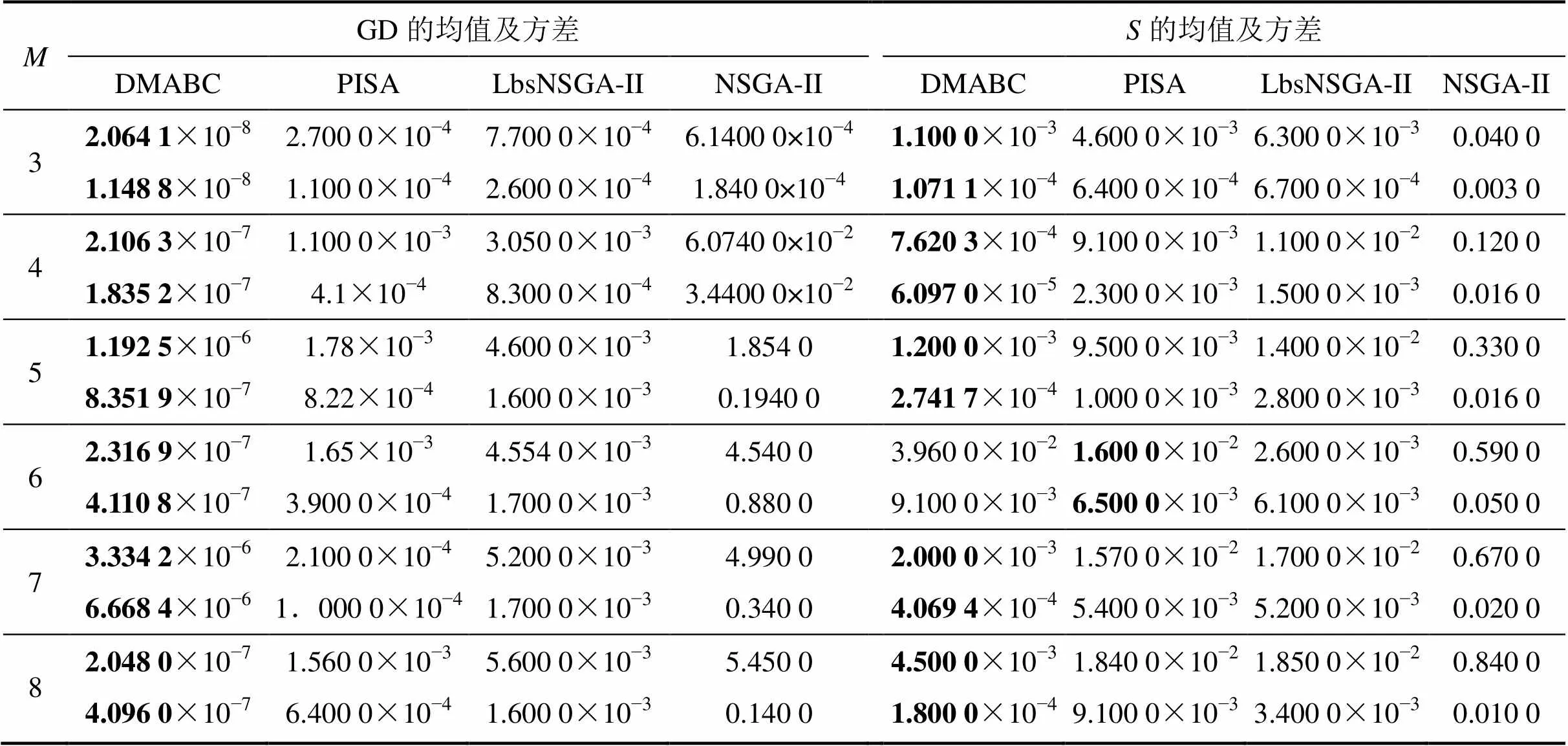
表2 各种算法对3~8个目标的DTLZ2问题的测试结果

注：为目标数目；各目标第1行数值表示均值，第2行数值表示方差，黑体数为每个测试函数所得最优结果。

从表2可以看出：对于3~8个目标的DTLZ2和DTLZ3问题，本文算法的世代距离均值远远比其他3种算法的小，说明本文算法更可以收敛至最优的非支配前沿，其收敛性对各测试函数都优于其他3种对比算法，且GD的方差很小，表明本文算法具有很高的稳定性，能在各次测试中均收敛至理想非支配前沿；在5个目标以上的DTLZ2问题上，NSGA-II的均值较大，表明它极易陷入局部Pareto前沿，收敛性较差，而对3个目标以上的DTLZ3问题，所获方差较大，证明该算法并不稳定；PISA和LbsNSGA-II算法所获GD均值、方差均比NSGA-II的小，表明PISA和LbsNSGA-II的收敛性优于NSGA-II，但比本文算法的收敛性差很多。对于3~8个目标的DTLZ3问题可得出类似结论。

从表2可以看出：除在6个目标的DTLZ2问题和8个目标的DTLZ3问题上，PISA算法的分布性均值最小外，本文算法的均值都最小。这表明本文算法在大多测试问题上都可以获得最佳的分布效果，对高维多目标优化具有良好的分布性能，且所获方差较小，表明本文算法的稳定性较好。对于3~8个目标的DTLZ3问题可得出类似结论。分布性指标只能反映解集的分布是否均匀，但不能直观反映解集是否覆盖整个Pareto前沿，为此这里又给出5个目标和8个目标DTLZ2问题的优化结果分布图，可以直观显示解集覆盖能力，如图2所示。

(a) 5个目标；(b) 8个目标

图2中纵坐标表示在各目标上可以取得的数据范围，数据范围越宽，表明解集覆盖范围越大。由于PISA算法的收敛效果和分布效果都优于LbsNSGA-II和NSGA-II算法，这里仅给出与PISA算法的对比结果。对于5个目标的DTLZ2问题，PISA算法在前4个目标上的覆盖范围均为0.3~0.5，在第5个目标上的覆盖范围为0.2~0.5，而本文算法在各目标上的覆盖范围都可达到理论范围0~1；对于8个目标的DTLZ2问题，PISA算法在各目标上的分布范围都为0~0.5，而本文算法在各目标上的覆盖范围接近理论范围0~1，这说明与PISA算法相比，本文算法所获得的解集覆盖范围更宽。

上述实验从收敛效果、分布效果、解集覆盖能力方面证明本文提出方法可以较好地解决高维多目标优化问题。这是由于本文采用一种新的适应值评价方式、改进人工蜂群算法并综合使用CAO操作增大种群向最优前沿进化的压力、加快算法收敛速度并在一定程度上避免收敛于局部最优非支配前沿，使种群迅速收敛到最优的Pareto前沿，而后期使用分布性维护策略使聚集于某一区域的种群依靠Harmnic距离分散，获得很好的覆盖和分布效果。

5 结论

1) 借鉴并改进了MDMOEA算法中的适应值评价方式，并对人工蜂群算法进行改进，迫使种群迅速收敛于最优的非支配前沿。

2) 为避免算法获得的最优解聚集于某一区域，提出分布性维护措施.通过对3~8个目标的DTLZ2和DTLZ3问题进行测试，并与其他几种多目标优化算法对比，本文方法获得的非支配解更接近于真实的Pareto前沿，分布更加均匀、宽广。这表明本文方法是一种有效的高维多目标优化方法，不仅在实际应用中具有广泛的推广价值，而且扩展了人工蜂群算法的应用领域。

[1] 杨咚咚, 焦李成, 公茂果, 等.求解偏好多目标优化的克隆选择算法[J]. 软件学报, 2010, 21(1): 14−33. YANG Dongdong, JIAO Licheng, GONG Maoguo, et al. Clone selection algorithm to solve preference multi-objective optimization[J]. Journal of Software, 2010, 21(1): 14−33.

[2] Deb K, Kumar A. Light beam search based multi-objective optimization using evolutionary algorithms[C]//2007 IEEE Congress on Evolutionary Computation(CEC' 2007). Singapore, 2007: 2125−2132.

[3] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182−197.

[4] Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(1): 687−697.

[5] 暴励, 曾建潮. 一种双种群差分蜂群算法[J]. 控制理论与应用, 2011, 28(2): 266−272. BAO Li, ZENG Jianchao. A bi-group differential artificial bee colony algorithm[J]. Control Theory & Application, 2011, 28(2): 266−272.

[6] Ramin H, Bahareh H, Reza A, et al. A multi-objective artificial bee colony for optimizing multi-objective problems[C]//2010 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE). Chengdu, China: IEEE Press, 2010: 5277−5281.

[7] Sulflow A, Drechsler N, Drechsler R. Robust multi-objective optimization in high dimensional spaces[C]//Evolutionary Multi-Criterion Optimization: 4th International Conference EMO2007. New Yok: Springer−Verlag, 2007: 715−726.

[8] Hughes E J. Multiple single objective Pareto sampling[C]//2003 Congress on Evolutionary Computation. Canberra, Australia, 2003: 2678−2684.

[9] Hughes E J, MSOPS-II: A general-purpose many-objective optimizer[C]//2007 IEEE Congress on Evolutionary Computation (CEC’2007). Singapore, 2007: 3944−3951.

[10] Saxena D K, Deb K. Certain large-dimensional multi-objective optimization problems: Employing correntropy and a novel maximum variance unfolding[C]//Evolutionary Multi-Criterion Optimization: 4th International Conference, EMO2007. New York: Springer−Verlag, 2007: 772−787.

[11] ZOU Xiufen, CHEN Yu, LIU Minzhong, et al. A new evolutionary algorithm for solving many-objective optimization problems[J]. IEEE Transactions on Systems, MAN, and Cybernetics. Part B: Cybernetics, 2008, 38(5): 1402−1412.

[12] Salem F A, Tony J D, Griffin I A, et al. Convergence acceleration operator for multiobjective optimization[J]. IEEE transactions on Evolutionary Computation, 2009, 13(4): 825−847.

[13] HuangV L, SuganthanP N, Qin A K, et al. Multi-objective differential evolution with external archive and harmonic distance-based diversity measure[R]. Singapore: Technical Report of Nanyang Technological University, 2005: 1−24.

[14] Penev K, Littlefair G. Free search: A comparative analysis[J]. Information Sciences, 2005, 172(1): 173−193.

[15] ZHANG Bin, REN Weihua, ZHAO Lihua, et al. Immune system multiobjective optimization algorithm for DTLZ problems[C]//2009 Fifth International Conference on Natural Computation. Tianjin, China: IEEE, Press, 2009: 603−607.

(编辑 陈灿华)

Optimization of multi-objective problems based on artificial bee colony algorithm

WANG Yanjiao1, 2, XIAO Jing2, 3

(1. College of Information Engineering, Northeast Dianli University, Jilin 132002, China; 2. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China; 3. College of Information Engineering, Liaoning Provincial College of Communications, Shenyang 110122, China)

In order to improve the convergence and diversity of large-dimensional multi-objective optimization algorithms, a novel large-dimensional multi-objective optimization algorithm based on an improved artificial bee colony algorithm was proposed. Firstly, an improved fitness evaluation method was employed to measure the superiority of every individual quantitatively. Secondly, artificial bee colony algorithm was improved to make the population converge reach the true Pareto front quickly. Finally, a novel diversity-maintaining scheme was established to make the solution set distribute uniformly and cover the whole Pareto front. The results show that the diversities and convergence of the proposed algorithm are better than other state-of-the-artlarge-dimensional multi-objective optimization algorithms such as PISA.

large-dimensional multi-objective optimization; artificial bee colony algorithm; fitness evaluation method; diversity-maintaining scheme

10.11817/j.issn.1672-7207.2015.06.019

TP393

A

1672−7207(2015)06−2109−09

2014−06−20；

2014−08−20

国家自然科学基金资助项目(61175126)；教育部博士点基金资助项目(20112304110009)；东北电力大学博士科研启动基金资助项目(BSJXM-201320)；辽宁省博士科研启动基金资助项目(201205118)；辽宁省教育厅科学技术研究一般项目(L2012458)；黑龙江省博士后基金资助项目(LBH-Z12073)(Project (61175126) supported by the National Natural Science Foundation of China; Project (20112304110009) supported by the Ministry of Education Doctoral Fund; Project (BSJXM-201320) supported by the PhD Research Funds of Northeast Dianli University; Project (201205118) supported by Scientific Research Foundation of Liaoning Province; Project (L2012458) supported by the General Project of Science and Technology of Education Department of Liaoning Province; Project (LBH-Z12073) supported by the Heilongjiang Postdoctoral Fund)

王艳娇，博士，副教授，从事智能计算、智能信息处理研究；E-mail：wangyanjiao1028@126.com