鲁棒的加权孪生支持向量机

花小朋，丁世飞



鲁棒的加权孪生支持向量机

花小朋1, 2，丁世飞2, 3

(1. 盐城工学院信息工程学院，江苏盐城，224051；2. 中国矿业大学计算机科学与技术学院，江苏徐州，221116；3. 中国科学院计算技术研究所智能信息处理重点实验室，北京，100190)

基于局部信息的加权孪生支持向量机(WLTSVM)借用类内及类间近邻图分别表示类内样本的紧凑性和类间样本的分散性，克服孪生支持向量机(TWSVM)欠考虑训练样本间相似性的缺陷，并且在一定程度上降低二次规划求解的计算复杂度。然而，WLTSVM仍不能充分刻画类内样本潜在的局部几何结构，并且存在对噪声点敏感的风险。基于以上不足，提出一种鲁棒的加权孪生支持向量机(RWTSVM)。与WLTSVM相比，RWTSVM的优势在于：选用热核函数定义类内近邻图权值矩阵，可以更好地刻画类内样本潜在的局部几何结构及蕴含的鉴别信息；用类间近邻图选取边界点，同时结合类内近邻图使得超平面远离边界点中权重较大的样本，降低算法对噪声点敏感的风险。人造数据集和真实数据集上的测试结果验证算法RWTSVM的有效性。

孪生支持向量机；局部几何结构；噪声点；鲁棒性；分类

对于二分类问题，传统支持向量机(SVM)依据大间隔原则生成分类超平面，存在的缺陷是计算复杂度高且没有充分考虑样本的分布[1,2]。近年来，作为SVM的拓展方向之一，以孪生支持向量机(TWSVM)[3]为主要代表的非平行超平面分类器(NHCs)[4]正逐渐成为模式识别领域新的研究热点。TWSVM思想源于广义特征值近似支持向量机(GEPSVM)[5]，将GEPSVM问题转换为两个规模较小的形如SVM的二次规划问题，计算复杂度缩减为SVM的1/4。除了速度上的优势，TWSVM继承了GEPSVM的优势，即线性模式下能够较好地处理异或(XOR)问题。基于TWSVM，近年发展了许多改进方法[6−10]。特别是文献[6]提出的基于局部信息的加权孪生支持向量机(WLTSVM)，借用类内及类间近邻图分别表示类内样本的紧凑性和类间样本的分散性，克服了孪生支持向量机(TWSVM)欠考虑训练样本间相似性的缺陷。相比于TWSVM和WLTSVM不仅具有更好的泛化性能，而且选取少量边界点作为支持向量，进一步降低了二次规划求解的计算开销。然而，WLTSVM仍然存在如下不足：1) 简单的类内近邻图权值矩阵的定义不能充分的刻画类内样本潜在的局部几何结构，容易影响算法的泛化性能；2) 用类间近邻图选取相反类中少量边界样本点进行算法求解，很大程度上降低了计算复杂度，但这同时也提高了算法对噪声点敏感的风险。基于上述不足，本文提出一种鲁棒的加权孪生支持向量机(RWTSVM)。相比于WLTSVM，RWTSVM的优势在于：1) 选用热核函数定义类内权值矩阵，RWTSVM能更好地刻画类内样本潜在的局部几何结构及蕴含的鉴别信息；2) 用类间近邻图选取相反类中少量边界样本点进行二次规划求解，并且结合类内近邻图使得超平面远离边界点中权重较大的样本，这使得RWTSVM不敏感于噪声点；3) RWTSVM在保证计算复杂度相当的情况下具有更好的分类能力。

1 鲁棒的加权孪生支持向量机(RWTSVM)

1.1 线性RWTSVM

给定两类维实数空间中个训练样本点，分别用1×的矩阵和2×的矩阵表示第1类(+1类)和第2类(−1类)。这里，1和2分别是两类样本的数目，，，表示第(=1，2)类的第个样本。线性RWTSVM的目标是在维空间中寻找2个超平面：

要求每个类超平面离本类具有高密度相关的样本点尽可能近，离相反类中具有较大权重的边界样本点尽可能远。

为此，受谱图理论启发[7, 11]，针对每一类超平面，构造一对近邻图G和G分别刻画类内样本的紧凑性及类间样本的分散性。

其中：为热核参数.

定义2[6]考虑第1类样本，给定第2类中任意样本(=1，2，…，2)，则图G的权值矩阵可定义为：

依据定义2，第2类中每一个样本定义权重

定义3 线性RWTSVM的第1类超平面的优化准则(RWTSVM1)为

第2类超平面的优化准则(RWTSVM2)为

其中：1和2为惩罚参数，和为损失变量。

定义3中式(5)优化目标函数第1项要求第1类的超平面离本类中权重较大的样本尽可能近，相反，那些权重较小的样本点对超平面的影响不大。约束条件要求第2类中相对于第1类的边界点离超平面的距离至少为。事实上，越大(即越属于第2类)，样本离超平面越远。式(6)具有相似的几何解释。式(5)和(6)用矩阵形式分别表示为

(RWTSVM1)

和

(RWTSVM2)

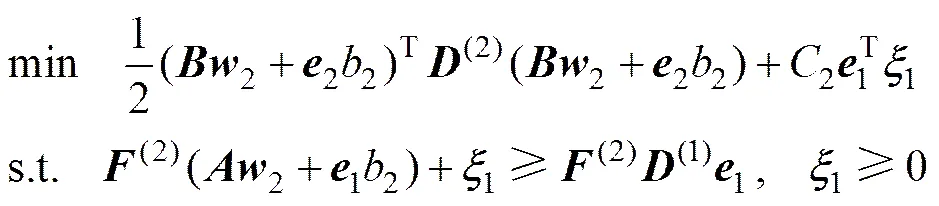
其中：1=(，…，)T，2=(，…，)T，1和2是2个实体为1的列向量，，。

定理1 线性RWTSVM优化准则式(7)对应的对偶问题(DRWTSVM1)为

优化准则式(8)对应的对偶问题(DRWTSVM2)为

其中：=[1]，=[2]。

证明。考虑线性RWTSVM的优化准则式(7)，对应的拉格朗日函数为

根据Karush-Kuhn-Tucker(KKT)条件可得：

令=[1]，=[2]，由式(12)和(13)可推得

将式(14)和(15)代入式(11)得定理1中对偶问题式(9)成立。

同理可证得定理1中对偶问题式(10)成立，且

证毕。

通过求解定理1中2个对偶问题，可以分别求得拉格朗日系数和，并在此基础上求出两类样本的决策超平面式(1)。线性RWTSVM的决策函数为

从式(15)和(16)可知：RWTSVM在求解过程中需要计算(T(1))−1和(T(2))−1，而(T(1))和(T(2))是正半定矩阵，因此，该方法不是严格的凸规划问题(强凸问题)，特别是在小样本情况下确实存在矩阵的奇异性。实际应用中，可以采用文献[3, 5−6]方法通过引入规则项(＞0)解决RWTSVM存在的奇异性问题，即(T(1))-1和(T(2))−1分别用(T(1)+)−1和(T(2)+)−1替代，尽可能的小。

1.2 非线性RWTSVM

当样本内在的几何结构呈现出高维非线性流行时，线性RWTSVM方法不能得到非线性流行结构的，因此本文进一步提出基于核空间(KFS)的非线性RWTSVM(NRWTSVM)方法。NRWTSVM优化目标是在高维核空间中寻找2个超平面：

其中：=[TT]T。

定义4 NRWTSVM的第1类超平面的优化准则(NRWTSVM1)为

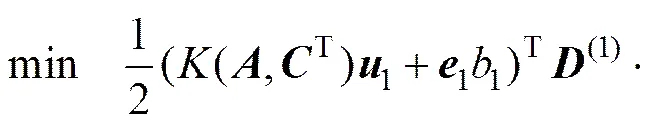
(19)

第2类超平面的优化准则(NRWTSVM2)为

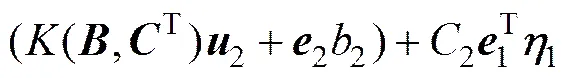
定理2 NRWTSVM优化准则式(19)对应的对偶问题(DNRWTSVM1)为

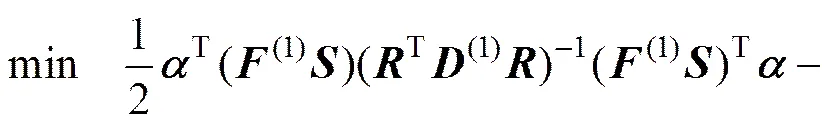
(21)

NRWTSVM优化准则式(20)对应的对偶问题(DNRWTSVM2)为

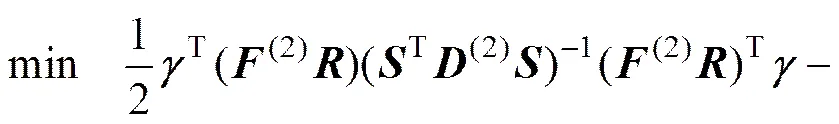
其中：=[(，T)1]，=[(，T)2]。

证明：考虑NRWTSVM的优化准则式(19)，对应的拉格朗日函数为

根据Karush-Kuhn-Tucker(KKT)条件可得：

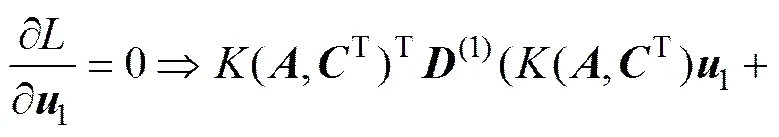
(25)

令=[(，T)1]，=[(，T)2]，由式(24)和(25)可推得

将式(26)和(27)代入式(23)得定理2中对偶问题式(21)成立。

同理可证得定理2中对偶问题式(22)成立，且

证毕。

NRWTSVM的决策函数为

2 RWTSVM与WLTSVM比较

2.1 泛化性能比较

WLTSVM第1类超平面的优化准则(WLTSVM1)为

显然，与本文定义1中式(2)不同。图1所示为RWTSVM和WLTSVM在人造数据集上的决策超平面。RWTSVM明显区别于WLTSVM。RWTSVM的2个超平面反映了2类样本的内在局部几何结构，而WLTSVM没有能够充分反映2类样本内在的局部几何结构。尽管2种算法对图1中人造数据集都可以得到100%学习精度，但从泛化性能层面上讲，RWTSVM明显优于WLTSVM。这充分说明WLTSVM中类内近邻图G的权值矩阵定义没有本文RWTSVM中的合理。事实上，当式(2)中热核参数时，等价于式(31)，这说明WLTSVM是本文RWTSVM的特例。

图1 RWTSVM与WLTSVM在人造数据集上的决策超平面

进一步考虑WLTSVM1优化准则式(30)中约束条件，可以看出：WLTSVM1是利用相反类中部分边界样本点()来构造限制约束。这在很大程度上降低了二次规划求解的计算复杂度，但是，若边界点中存在噪声点，则可能会影响到算法的泛化性能。与WLTSVM1相比，本文提出的RWTSVM1优化准则式(5)中约束条件中不仅考虑的是的样本点，而且还考虑到这些边界样本点的类内权重(即权重越大，离超平面的距离越远)。这样，不仅能够保证算法具有较低的计算复杂度，而且可以很好地克服噪声点问题。

2.2 计算复杂度比较

本文RWTSVM在训练阶段需要求解2个规模较小的二次规划问题，计算复杂度为，其中和分别为第1类样本及第2类样本中相应边界样本点数。除此之外，还要求出每个样本的类内权重及类间权重，计算复杂度分别为和。分析WLTSVM可知，本文RWTSVM在训练过程中需要花费计算开销的部分与WLTSVM完全类似，因此本文RWTSVM与WLTSVM计算复杂度相当。

3 实验分析

在人工数据集和真实数据集上分别对TWSVM，WLTSVM与RWTSVM进行实验。实验环境：Windows 7 操作系统，CPU为i3-2350M 2.3GHz，内存为2GB，运行软件为MATLAB 7.1。

3.1 测试人造数据集

相对于传统支持向量机，线性模式下对XOR问题的求解能力是NDCs算法优势之一[3−5]。图2所示为TWSVM，WLTSVM与RWTSVM 3个分类器在交叉数据集上“Crossplanes”(XOR的推广)[3,5]上的分类性能。显然3个算法产生的分类面重合，而且可以较好的求解XOR问题，并得到100%的学习精度。这也进一步证明了本文RWTSVM继承了NDCs算法的特色，即线性模式下对XOR问题的求解能力优于传统支持向量机算法。

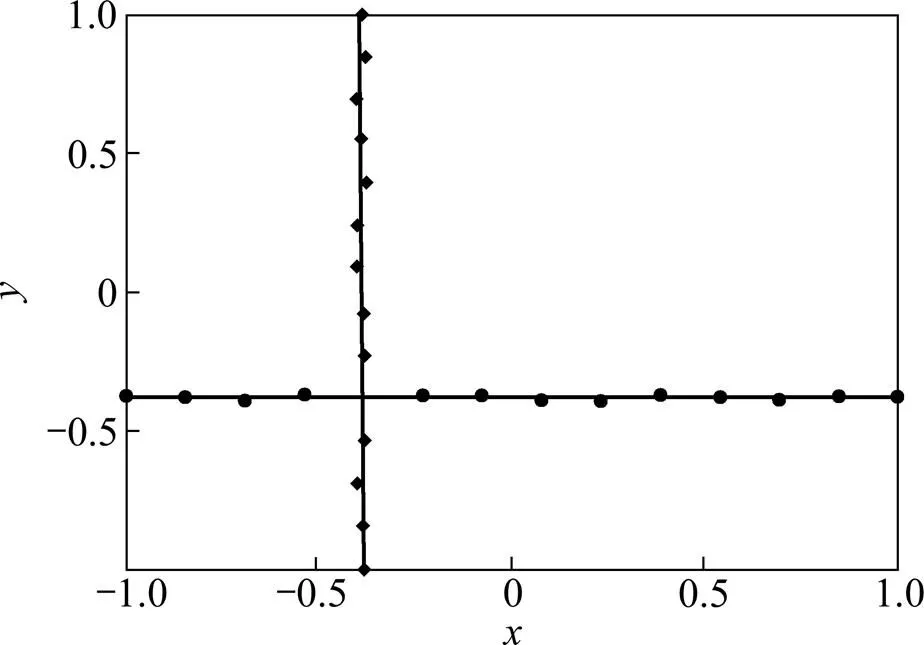
图2 TWSVM，WLTSVM和RWTSVM在交叉数据集上产生的分类面

3.2 测试真实数据集

为了更全面地说明本文RWTSVM分类方法具有的分类性能，在本节测试UCI数据集，同时与TWSVM，WLTSVM进行对比，以增加本文算法分类性能的说服力。

UCI数据集经常被用来测试算法的分类精 度[3−6,12−15]。在该测试阶段，抽取该数据集多个分类数据子集来分别测试TWSVM，WLTSVM和本文RWTSVM。对于每个数据子集，选用10-折交叉验证方法[3−6]。实验结果给出了平均识别精度和训练时间。参数1与2的搜索范围均为{2|=−8，−6，…，8}(简单起见，实验中令1=2)，=1×10−6，热核参数的搜索范围为{2|=−3，−2，…，6}，类内近邻参数的搜索范围为{1，2，…，9}，类间近邻参数设为5。非线性算法采用高斯核函数,核宽参数的搜索范围为{2|=−1，0，…，7}。表1和表2所示分别为线性模式及非线性模式下3种分类方法的测试结果。

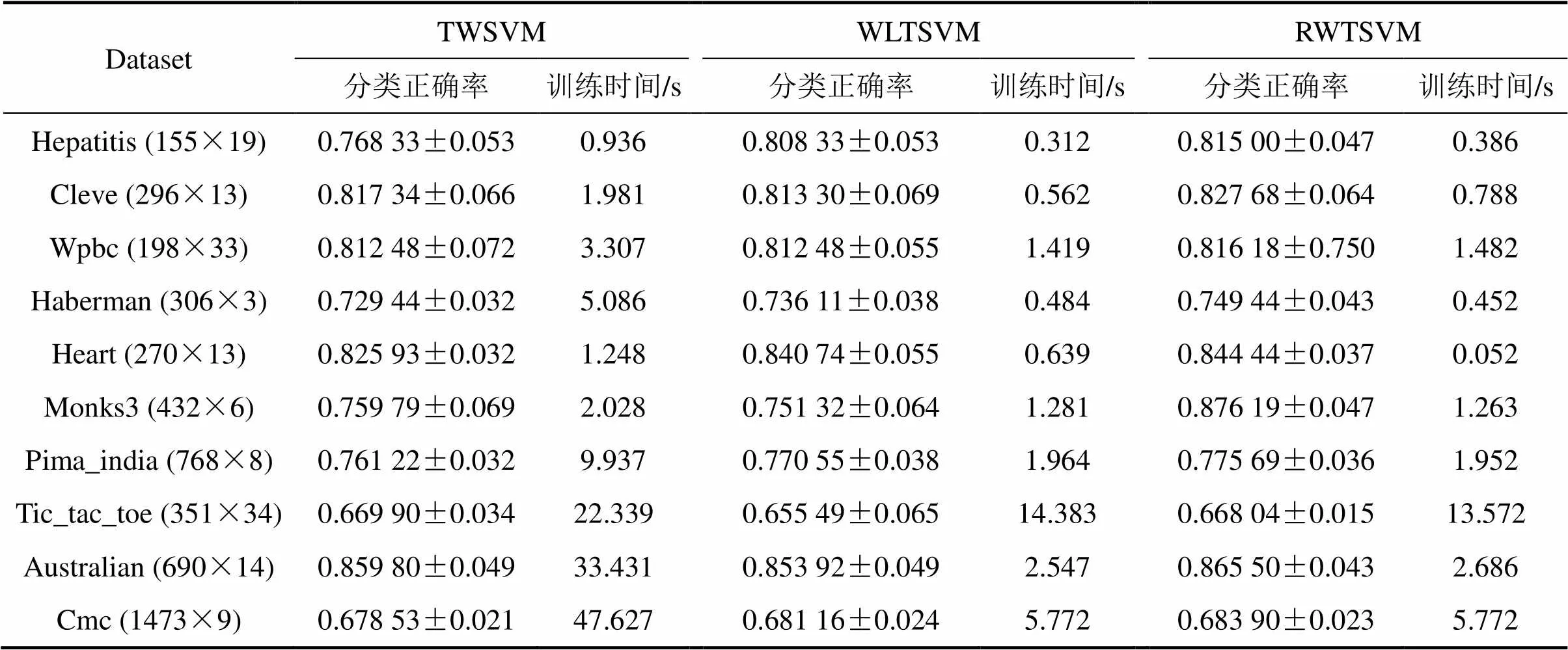
表1 线性TWSVM，WLTSVM与RWTSVM的测试结果

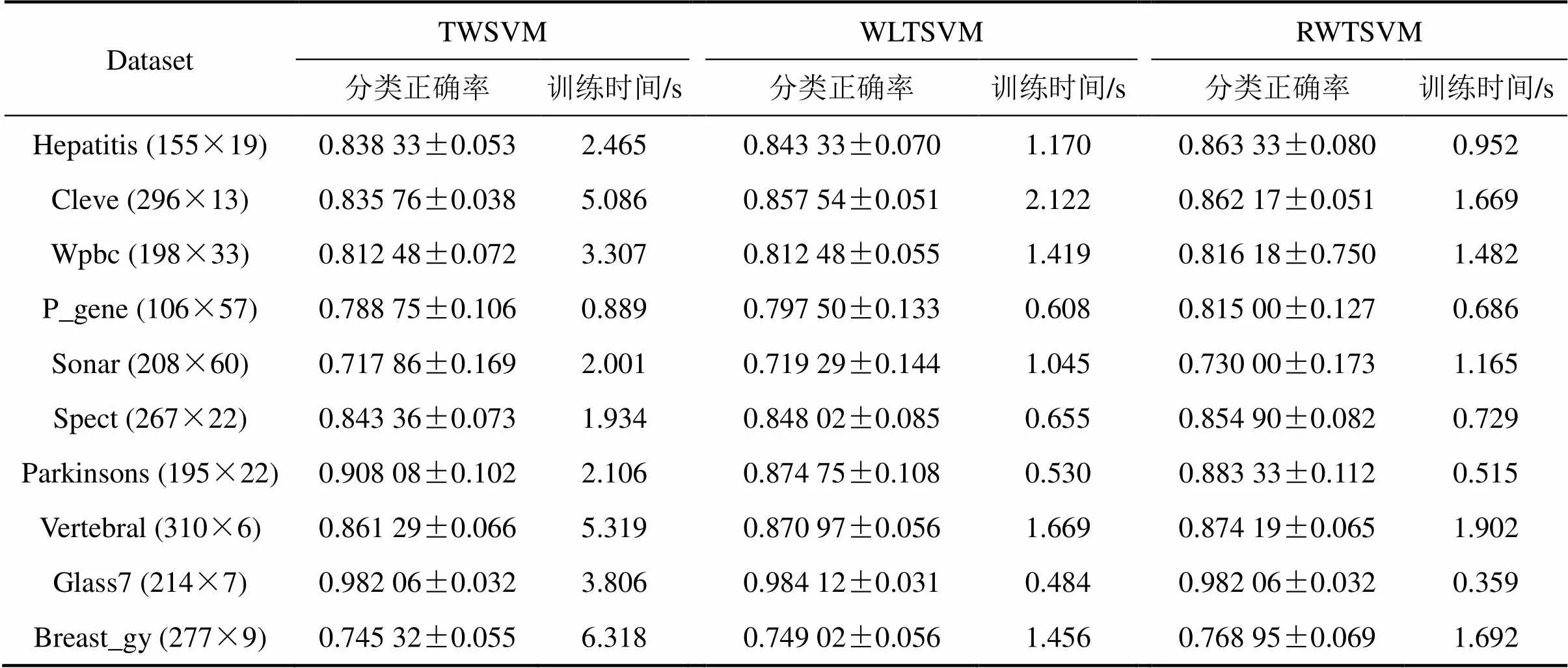
表2 非线性TWSVM，WLTSVM与RWTSVM的测试结果

从训练时间上看：本文RWTSVM与WLTSVM相当，这与2.2节计算复杂度分析一致；但训练速度明显比TWSVM快，这主要是因为TWSVM用相反类全部样本进行二次规划求解，而RWTSVM与WLTSVM用少量边界样本点求解。

从泛化性能上看：WLTSVM分类性能优于TWSVM，这点在文献[6]中已经得到验证；相比于WLTSVM，本文提出的RWTSVM 算法具有更好的分类能力，这也进一步验证了本文的改进措施确实可取。

4 结论

针对WLTSVM方法存在的不足，提出一种改进的NHCs方法：鲁棒的加权孪生支持向量机(RWTSVM)。该方法不仅继承了NHCs方法较好的异或(XOR)问题的求解能力，而且在一定程度上克服了WLTSVM方法不能充分刻画训练样本间局部几何结构信息以及对噪声点敏感的缺陷。理论分析及实验结果均证明了本文提出的改进措施切实可行。当训练样本数目趋向于大样本时，RWTSVM与WLTSVM类似，会因计算复杂度过高而难于处理，因此，进一步研究计划将着力于解决大样本学习问题。

[1] 皋军, 王士同, 邓赵红. 基于全局和局部保持的半监督支持向量机[J]. 电子学报, 2010, 38(7): 1626−1633. GAO Jun, WANG Shitong, DENG Zhaohong. Global and local preserving based semi-supervised support vector machine[J]. Acta Electronica Sinica, 2010, 38(7): 1626−1633.

[2] 花小朋, 丁世飞. 局部保持对支持向量机[J]. 计算机研究与发展, 2014, 51(3): 590−597. HUA Xiaopeng, DING Shifei. Locality preserving twin support vector machines[J]. Journal of Computer Research and Development, 2014, 51(3): 590−597.

[3] Jayadeva, Khemchandai R, Chandra S. Twin support vector machines for pattern classification[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2007, 29(5): 905−910.

[4] DING Shifei, HUA Xiaopeng, YU Junzhao. An overview on nonparallel hyperplane support vector machines[J]. Neural Computing and Applications, 2014, 25(5): 975−982.

[5] Mangasarian O L, Wild E. MultisurFace proximal support vector machine classification via generalized eigenvalues[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(1): 69−74.

[6] YE Qiaolin, ZHAO Chunxia, GAO Shangbing, et al. Weighted twin support vector machines with local information and its application[J]. Neural Networks, 2012, 35(11): 31−39.

[7] YE Qiaolin, ZHAO Chunxia, YE Ning, et al. Localized twin svm via convex minimization[J]. Neurocomputing, 2011, 74(4): 580−587.

[8] PENG Xinjun, XU Dong. Norm-mixed twin support vector machine classifier and its geometric algorithm[J]. Neurocomputing, 2013, 99(1): 486−495.

[9] QI Zhiquan, TIAN Yingjie, SHI Yong. Structural twin support vector machine for classification[J]. Knowledge-Based Systems, 2013, 43(5): 74−81.

[10] SHAO Yuanhai, DENG Naiyang, YANG Zhimin, et al. Probabilistic outputs for twin support vector machines[J]. Knowledge-Based Systems, 2012, 33(9): 145−151.

[11] YANG Xubing, CHEN Songcan, CHEN Bin, et al. Proximal support vector machine using local information[J]. Neurocomputing, 2009, 73(1): 357−365.

[12] WANG Xiaoming, CHUANG Fulai, WANG Shitong. On minimum class locality preserving variance support vector machine[J]. Patter Recognition, 2010, 43(8): 2753−2762.

[13] CHEN Xiaobo, YANG Jian, YE Qiaolin, et al. Recursive projection twin support vector machine via within-class variance minimization[J]. Pattern Recognition, 2011, 44(10): 2643−2655.

[14] 丁立中, 廖士中. KMA-a: 一个支持向量机核矩阵的近似计算算法[J]. 计算机研究与发展, 2012, 49(4): 746−753. DING Lizhong, LIAO Shizhong. KMA-a: A kernel matrix approximation algorithm for support vector machines[J]. Journal of Computer Research and Development, 2012, 49(4): 746−753.

[15] XUE Hui, CHEN Songcan. Glocalization pursuit support vector machine[J]. Neural Computing and Applications, 2011, 20(7): 1043−1053.

(编辑 陈爱华)

Robust weighted twin support vector machine

HUA Xiaopeng1, 2, DING Shifei2, 3

(1. School of Information Engineering, Yancheng Institute of Technology, Yancheng 224051, China;2. School of Computer Science and Technology, China University of Mining and Technology, Xuzhou 221116, China;3. Key Laboratory of Intelligent Information Processing, Institute of Computing Technology,Chinese Academy of Science, Beijing 100190, China)

Weighted twin support vector machine with local information (WLTSVM), as a variant of twin support vector machine (TWSVM), uses within-class graph and between-class graph to characterize the intra-class compactness and the inter-class separability, respectively. This makes WLTSVM improve the generalization capability of TWSVM by mining as much underlying similarity information within samples as possible and reduces the time complexity of TWSVM by reducing the support vectors for each class. Despite these advantages, WLTSVM can not fully reflect the local geometry manifold within samples because of using the within-class graph whose weight matrix is defined simply. Moreover, WLTSVM ignores the possible outliers because it chooses boundary points in the contrary class to construct the constraints. Thus a novel method, robust weighted twin support vector machine (RWTSVM) was proposed, which can better characterize the underlying local geometric structure and the descriminant information by using a hot kernel function to define the weight matrix of within-class graph, and reduce the influence of outliers by considering within-class weight of the boundary points used to construct constraints in WLTSVM. The experimental results on the artificial and real datasets indicate the effectiveness of RWTSVM method.

twin support vector machine; local geometric structure; outliers; robust; classification

10.11817/j.issn.1672-7207.2015.06.014

TP391.4

A

1672−7207(2015)06−2074−07

2014−06−13；

2014−08−20

国家重点基础研究发展计划(973 计划)项目(2013CB329502)；国家自然科学基金资助项目(61379101) (Project (2013CB329502) supported by Major State Basic Research Development Program of China; Project (61379101) supported by the National Natural Science Foundation of China)

花小朋，副教授，博士研究生，从事机器学习与数据挖掘研究；E-mail：xp_hua@163.com