基于粗糙集和粒子群优化支持向量机的滑坡变形预测

赵艳南，牛瑞卿，彭令，程温鸣



基于粗糙集和粒子群优化支持向量机的滑坡变形预测

赵艳南1，牛瑞卿1，彭令2，程温鸣3, 4

(1. 中国地质大学(武汉) 地球物理与空间信息学院，湖北武汉，430074；2. 中国地质环境监测院，北京，100081；3. 中国地质大学(武汉) 工程学院，湖北武汉，430074；4. 三峡库区地质灾害防治工作指挥部，湖北宜昌，443000)

以三峡库区白水河滑坡为例，首先分析降雨量与库水位等影响因素与滑坡变形特征的响应关系，然后利用粗糙集理论对10个初始影响因子进行属性约减，筛选出影响滑坡变形的核因子集，最后基于该因子集建立粒子群优化支持向量回归模型，对滑坡位移速率进行预测。研究结果表明：测试样本的预测结果与实测值变化趋势基本一致，其平均绝对误差为0.234 mm/d，均方差和判定系数分别为0.163和0.520。粗糙集理论在分析滑坡变形特征、筛选关键因子方面的适用性与科学性，构建的粗糙集−粒子群优化支持向量机模型具有较高的泛化能力，是一种有效的滑坡变形预测方法。

滑坡变形预测；粗糙集；粒子群优化；支持向量机

滑坡是一种严重的地质灾害，受坡体自身地质条件及降雨、库水、地下水和人类工程活动等多种因素影响，表现出非常复杂的非线性演化特征，其位移预测是当今滑坡研究领域的一个热点。近年来，时间序列模型、神经网络模型、灰色系统模型和支持向量机等模型被广泛应用到滑坡位移预测研究中，取得了较好的预测效果。李强等[1]利用时间序列分析方法建立了滑坡位移动态预报的差分自回归滑动平均(ARIMA)模型和多变量时间序列(CAR)模型。吴益平等[2]将滑坡位移分解为趋势项和具有不确定性的随机项，提出了灰色−神经网络预测模型。汤罗圣等[3]针对变形特征为阶跃型的滑坡，将滑坡位移分解为蠕变位移和波动位移，采用多项式拟合和灰色GM(1,1)模型分别对蠕变位移和波动位移进行预测。马文涛[4]在分析了灰色预测模型和最小二乘支持向量机各自的优缺点的基础上，提出了灰色最小二乘支持向量机预测模型。此类研究取得了较好的效果，但是均未分析外界影响因素与位移之间的响应关系，仅为时间因素单变量分析。杜鹃等[5]利用时间序列模型将位移分解为趋势项和周期项，并利用BP神经网络模型基于降雨量和库水位等外界影响因素对周期项位移进行了预测，取得了较好的预测效果。神经网络技术为非线性时间序列预测提供了有力的工具，但在实践中存在过学习以及隐层网络节点数选取缺乏理论指导等缺陷，削弱了它的预测能力。支持向量机是基于统计学习理论建立的，它以结构风险最小化原则取代传统机器学习方法中的经验风险最小化原则，既能有效地处理非线性数据，又能限制过学习；因此，构建基于外因响应的支持向量回归模型是科学可行的[6]。但由于滑坡变形的复杂性，外界影响因素众多，如果因子间存在耦合性和冗余性，势必会影响模型的效率和最后的结果，如何科学筛选核心因子，剔除冗余信息制约着模型的预测精度。粗糙集理论( RS)能够分析不精确数据，可对数据进行信息约简，剔除冗余信息，进而获得数据的核心知识，目前已经应用在滑坡区划研究中[7−8]。基于以上分析，本文作者以三峡库区白水河滑坡为例，分析滑坡变形与降雨和库水等影响因素的响应关系，将粗糙集理论和支持向量回归(SVR)模型有机结合，实现滑坡变形特征的综合分析及位移预测。

1 模型原理

1.1 粗糙集

粗糙集理论是Pawlak[9]于1982年提出的一种能够定量分析处理不精确、不一致和不完整信息与知识的数学工具。在粗糙集理论中1个知识表达系统可定义为

定义条件属性对决策属性的支持度为

式中：POS称为的正域，指那些根据知识能完全确定中归入集合的元素集合；表示在属性下能够确切划入决策类的对象比率，描述了条件属性对决策属性的支持程度。对于1个知识表达系统而言，各个条件属性对决策属性的贡献是不同的，将条件属性对决策属性的贡献称为该属性的重要性。一般可用去掉该属性后的决策表中分类能力的变化来区分该属性的重要性。在衡量由属性集导出的分类属性子集的重要性时，可用两者依赖程度的差来度量，即

式中：Δ表示当从集合中踢出某些属性子集′后进行分类时，分类的正域受其影响的程度。该值越大，说明相应的条件属性越重要。在1个决策表中，有些属性是不可缺少的，则称其为核属性。粗糙集理论给出了这种对知识约简和求核的方法，从而提供了从决策表中分析冗余属性的能力。

1.2 支持向量机

支持向量回归通过非线性变换将输入向量映射到高维特征空间，并构造最优决策函数，利用原空间的核函数取代高维特征空间中的点积运算，应用有限样本的学习训练，获得全局最优解[10]。SVR估计函数为

利用不敏感损失函数将估计函数转化为优化问题：

约束条件为

式(6)采用对偶理论转化成二次规划求解，则约束表达式的对偶式为

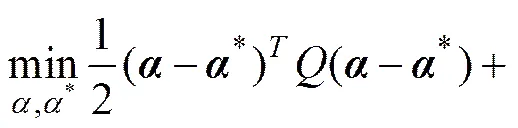
约束条件为

通过二次规划算法可得SVR回归预测模型为

1.3 粒子群优化支持向量机参数

粒子群算法(particle swarm optimization，PSO)在寻优过程中，每个优化问题的解均被认为是搜索空间中的1个粒子。每1个粒子都根据适应度函数计算出其适应值，且每个粒子还有1个速度，它们决定粒子飞翔的方向和距离。在每1次迭代过程中，粒子根据个体最优值(Best)和全局最优值(Best)来更新其速度和位置[11]。粒子群优化支持向量机参数的基本流程如下。

1) 随机产生初始粒子群，每1个粒子的当前位置分量对应于支持向量机参数，组成1个支持向量机。

2) 利用滑坡位移影响因子样本集，对构成的支持向量机进行训练。

4) 根据适应度最小化原则，评价粒子群中的所有个体，并从中找到最佳粒子，再将当前最佳粒子的适应度与已有的所有适应度比较，确定当前的Best和Best；并计算每个粒子的飞行速度，从而产生新的 粒子。

5) 若粒子的适应度值达到要求，或者已经达到最大迭代次数，则算法结束；否则转至步骤3)继续进行迭代。

2 滑坡变形特征分析

白水河滑坡为一特大型老滑坡，位于长江南岸，发育于秭归向斜西翼，出露地层为侏罗系下统香溪组中厚层状砂岩夹薄层状泥岩，为单斜顺层坡。滑坡南北向长度600 m，东西向宽度700 m，滑体平均厚度约30 m，体积为1 260×104m3。自实施专业监测以来，白水河滑坡已经发生数次变形，2004−07，根据白水河滑坡变形特征划定滑坡预警区[12]。对该滑坡监测方法主要为地表位移GPS监测、深部位移钻孔测斜监测，地下水位监测、地表裂缝相对位移监测和宏观地质巡查监测(见图1)。图1所示为白水河滑坡专业监测布置示意图。

图1 白水河滑坡专业监测布置示意图

图2所示为滑坡累积位移−时间曲线图。通过分析预警区内4个GPS监测点(ZG118，XD-01，XD-02和XD-03)的累积位移数据(见图2)，发现白水河滑坡的累积位移−时间曲线表现出明显的台阶状特征，分别在每年的5至9月份出现急剧上扬，10月份至次年的4月份趋于平稳。

监测点：1—ZG118；2—XD-01；3—XD-02；4—XD-03

例如2005−08—2005−09，2006−05—2006−07，2007−05—2007−08，2008−08—2008−09，2009−05—2009−06以及2010−06—2010−07，累积位移曲线出现明显的阶跃性，表明滑坡均发生加剧变形。

图3所示为降雨量、库水位、地下水位及滑坡累积位移曲线。从图3可知：该区降雨及库水位的季节性变化基本与各监测点的位移变化相互对应。汛期时白水河滑坡处于显著变形阶段，非雨季时处于缓慢变形阶段，而当库水位下降时，滑坡变形明显。

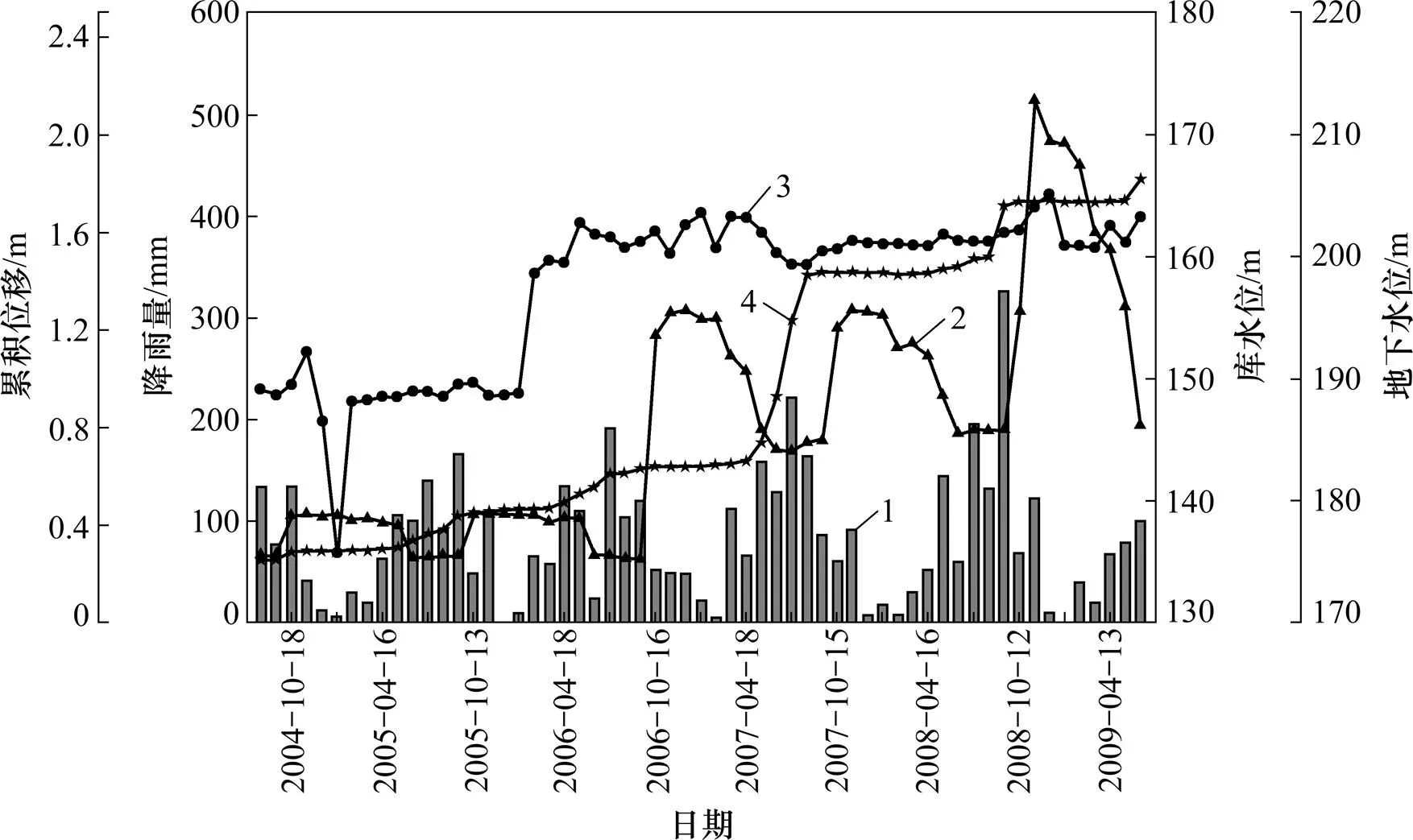
1—降雨量；2—库水位；3—地下水位；4—ZG118监测点累积位移

2007年是白水河滑坡专业监测以来变形最强烈的1年，滑坡出现显著的宏观拉张裂缝、剪切裂缝，滑坡东侧和后缘边界基本贯通，西侧裂缝呈羽状断续展布。分析原因发现：该区在2007−04—2007−07这4个月发生连续强降雨，降雨量分别为146.1，207.8，144.4和224.0 mm，仅2007−07−17—2007−07−24的连续降雨量就达到116.8 mm，特别是2007−07−24的强降雨，其降雨量达58.6 mm，高强度的降雨造成滑坡发生强烈变形。同时，三峡库水位由2007−02−06的155 m下降到2007−07−10的144.1 m，下降幅度达10.9 m，这是三峡库水位首次蓄水到156 m后下降到145 m，对滑坡变形造成极大影响。可见库水位下降及强降雨是2007年度白水河滑坡强烈变形的主要因素。

2008−07—2008−08降雨量分别为285.2 mm和298.6 mm，共583.8 mm，占全年降雨量的49.6%，特别是2008−08−29—2008−08−30这2 d累积降雨量就达89.6 mm。而2008−07—2008−09的库水位十分稳定，库水位一直在145 m附近微弱波动，对滑坡变形的影响极小。可见连续强降雨是本次白水河滑坡强烈变形的主要影响因素，但因没有库水位下降的叠加影响，其变形程度远比2007年的小。

2009−05−16—2009−07−24，三峡库水位为155.9~145.3 m，库水位下降10.6 m，2009−05和2009−06降雨量分别为124.2 mm和101.4 mm，特别是2009−06−28—2009−06−30降雨量达61.8 mm，在库水位降落及强降雨的作用下，导致白水河滑坡于2009−06—2009−07产生强烈变形。

综上所述，降雨及库水位下降是白水河滑坡变形的2个主要影响因素。在库水位下降及强降雨的共同作用下，滑坡发生的变形最剧烈；在库水位相对稳定或下降速率慢的情况下，滑坡变形取决于降雨量，但变形剧烈程度远比前者的小。

3 滑坡变形预测

3.1 变形预测流程

三峡大坝每年10月开始蓄水至高水位运行，至次年汛期开始泄洪至低水位运行，库水水位自2003年开始经历了2003−06蓄水到达135 m，2006−09蓄水到达156 m及2008−11蓄水到达175 m 3个阶段，自2009年开始保持145~175 m。为保证规律的一致性，本文作者选取2009−01—2012−12的滑坡累积位移速率及降雨量和库水位进行分析。

以GPS监测点ZG118累积位移速率(mm/d)为预测对象，降雨量及库水位为主要影响因素。首先根据前文分析，选取影响滑坡变形的相关降雨和库水初始影响因子，然后利用粗糙集原理进行与滑坡变形相关的属性约减，去掉冗余或者干扰因子，得到最小条件因子集和核；然后，以核因子作为支持向量机的输入因子集，构建滑坡位移速率与影响因子的支持向量机模型，最终实现对滑坡位移速率的预测。

3.1.1 影响因子选取

1) 降雨因子。通过前面分析可知，白水河滑坡变形主要与长时间连续降雨和突发性的强降雨有关，因此，选取当月平均降雨量(1)、当月累积降雨量(2)、两月累积降雨量(3)、当月日最大降雨量(4)、当月连续最大降雨量(5)、当月连续降雨天数(6)共6个因子作为初始因子。

2) 库水因子。当库水快速下降时滑坡变形强烈，而库水位上升时滑坡变形不明显，故选取当月库水位平均值(1)、当月库水位平均下降速率(2)、2月份库水位平均下降速率(3)及当月库水位波动速率(4)共4个因子进行研究。

3) 初始影响因子相关性计算。采用Pearson相关系数来分析10个影响因子的相关性，表1所示为影响因子相关系数。由表1可知：各影响因子间存在较强的耦合性和冗余性，直接以该因子集作为输入集进行预测会对预测结果造成一定的影响。

表1 影响因子相关系数

3.1.2 滑坡变形阶段划分

使用粗糙集理论进行滑坡变形特征分析与属性约减，首先需要确定决策属性和条件属性。本文作者将滑坡变形情况作为决策属性，目前一般通过对滑坡变形阶段的划分来显示滑坡变形特征。刘广润等[13]将滑坡的变形阶段分为蠕滑阶段、匀滑阶段、加速阶段、破坏阶段。图4所示为斜坡变形的3阶段演化图示。从图4可知：−为蠕滑阶段，这一阶段坡体表现出缓慢滑动；−为匀滑阶段，坡体表现为基本稳定，位移缓慢增加；−为加速阶段，坡体表现为快速变形。

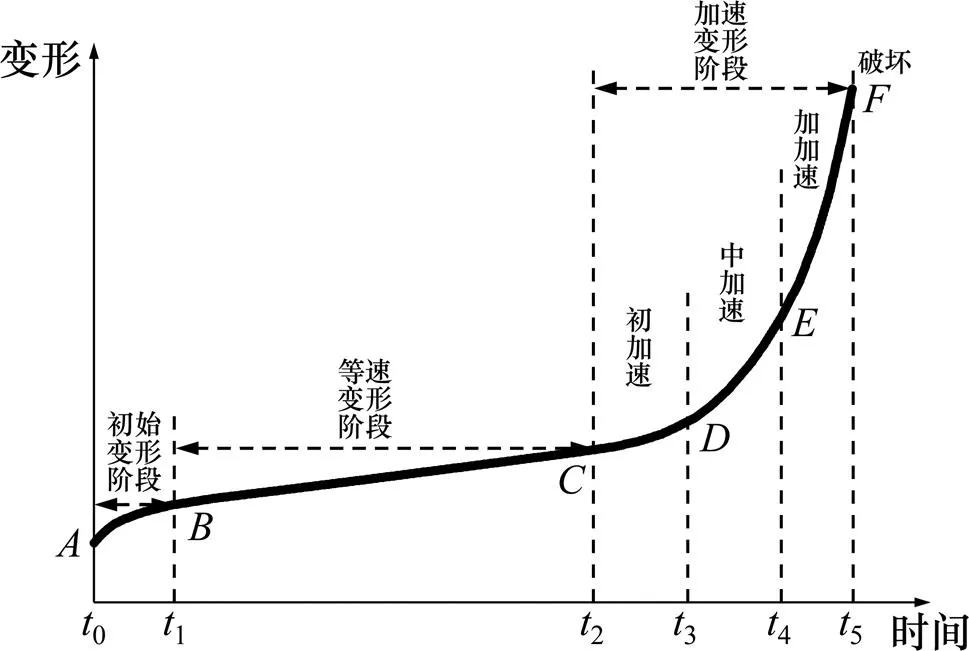
图4 斜坡变形的3阶段演化过程

在滑坡变形监测过程中，滑坡何时因为何种因素影响处于加速变形阶段是关注的重点，因此，本文作者利用K-means算法[14]针对累积位移速率进行聚类，结合滑坡变形监测资料分析将滑坡变形分为匀速变形阶段和加速变形阶段。图5所示为白水河滑坡变形阶段划分。由图5可知：划分阶段与前文分析的汛期滑坡加速变形和非雨季滑坡缓慢变形一致。

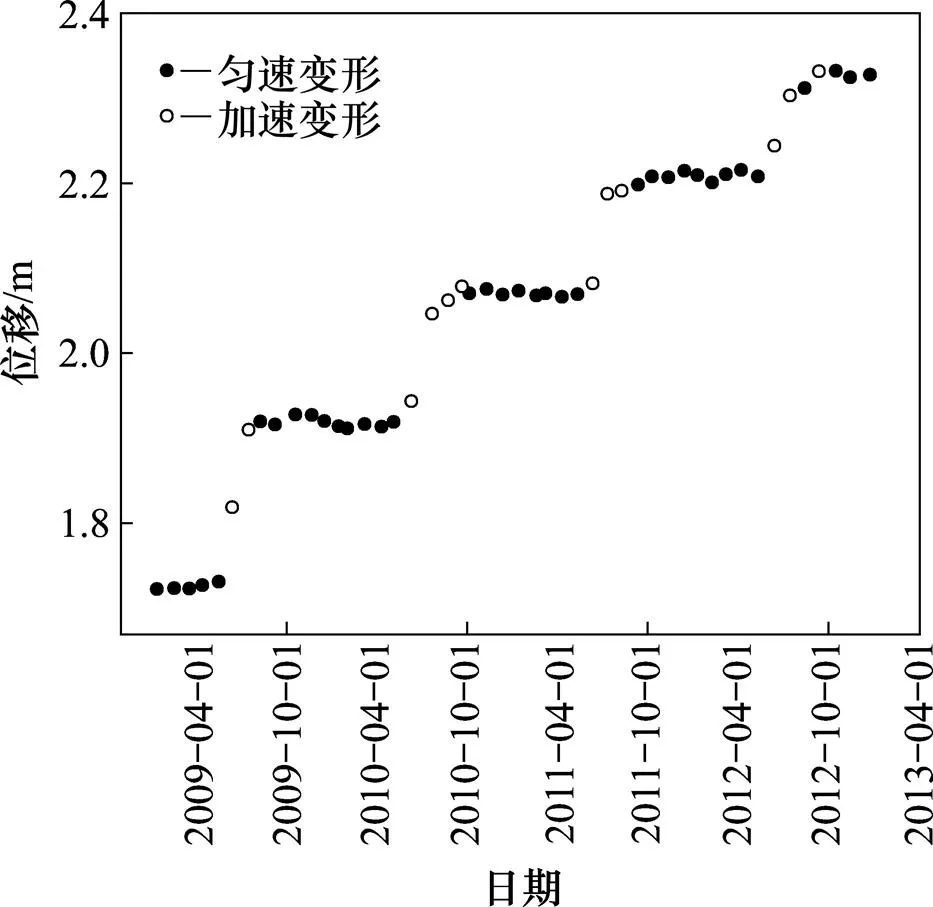
图5 白水河滑坡变形阶段划分

3.1.3 构建初始决策表

利用2009−01—2012−12的滑波累积位移速率及降雨量和库水位，将前面选取的10个影响因子作为条件属性，滑坡变形阶段作为决策属性，构成滑坡变形分析决策表。决策表中行对应滑坡所处的变形阶段，列对应该阶段的各影响因子。

3.1.4 属性约简

属性约简就是在保持知识库分类能力不变的条件下删除其中冗余或者干扰属性，筛选出能反映数据之间本质关系的关键属性。由于粗糙集要求输入的属性数据为离散型变量，文中选取的10个影响因子均为连续型变量，因此，需要先进行影响因子离散化处理，然后进行属性约简，去掉冗余属性，得到与滑坡变形相关的最小条件属性集和核，进而可以利用约简集提取滑坡变形的知识规则。本文作者利用RSES2 软件系统[15]进行相关处理，采用穷举算法(exhaustive algorithm)对决策表进行属性约减，最终得到1个与滑坡变形相关的核因子集：{当月平均降雨量，当月连续最大降雨量，当月库水位平均下降速率，当月库水位平均值}。对比表1中各影响因子的相关系数发现：粗糙集属性约减既能选出对滑坡变形影响最大的因子，同时又剔除了耦合性大的因子，降低了影响因子的冗余性。由4个核因子和滑坡变形决策属性重新构成新决策表，进而对决策表规则提取，得到与滑坡变形相关的知识规则，如表2所示。

表2 白水河滑坡变形决策规则

注：1为当月平均降雨量，mm；5为当月连续最大降雨量，mm；2为当月库水位平均下降速率，m；1为当月库水位平均值，m；±Inf 为对应影响因子极值；为滑坡变形阶段。

表2中：“强度”是指决策表中满足某条规则的对象个数；1和5为降雨影响因子，2和1为库水影响因子。匀速变形阶段的强度很大，表明白水河滑坡大部分时间处于匀速变形阶段，仅在降雨和库水位影响较大时处于加速变形阶段。通过分析可知：规则1说明{当月平均降雨量＜10.58 mm且当月连续降雨量＜36.90 mm且当月库水位平均下降速率＜0.24 m且当月库水位平均值＜146.59 m}即降雨量小、库水变化缓慢时白水河滑坡处于匀速变形阶段；规则4说明{当月平均降雨量＞10.58 mm且当月连续降雨量＞36.90 mm且0.24 m＜当月库水位平均下降速率＜0.55 m且当月库水位平均值＞146.59 m}即降雨量大、库水下降快时白水河滑坡处于加速变形阶段；规则2与规则4的库水情况一致，但降雨情况相反，即库水变化一致时，降雨量大也会影响滑坡加剧变形。规则5，6和7表明即使降雨量较小，但当库水位下降快时也会促使滑坡变形，这与前面分析的滑坡变形规律一致。

3.1.5 支持向量机模型的建立

1) 首先对约减后的核因子集{当月平均降雨量，当月连续最大降雨量，当月库水位平均下降速率，当月库水位平均值}和滑坡累积位移速率进行异常点剔除等预处理，然后将其归一化到0到1之间，消除不同量纲的影响。

2) 将滑坡累积位移速率及对应的核因子集数据按照时间段分成2部分，其中2009−01—2011−12的数据作为模型训练样本，2012−01—2012−12的数据为模型检验样本。

3) 设置PSO算法的初始参数，学习因子1为1.7，2均为2.0，惯性权重=0.6，种群规模25，最大迭代步数为300。然后搜索得到支持向量机的参数惩罚因子=6.025和径向基函数(RBF)参数=2。利用获得的最佳模型参数对样本数据进行学习，建立滑坡累积位移速率与影响因子之间的响应模型。

4) 利用所建立的模型对检验样本进行预测，检验模型的有效性和预测能力。

3.2 预测结果与分析

利用上述方法所建立的模型对白水河滑坡2009—2011年的训练样本进行拟合，构建基于核因子响应的滑坡位移速率预测模型(RS-PSO-SVR模型)，并利用该模型对2012年的测试样本进行预测，同时以影响滑坡变形的10个初始影响因子直接作为支持向量机模型的输入集，即不经过粗糙集属性约减分析，利用相同优化算法搜索模型参数，构建预测模型(PSO-SVR模型)，2种模型的拟合与预测结果如图6所示。

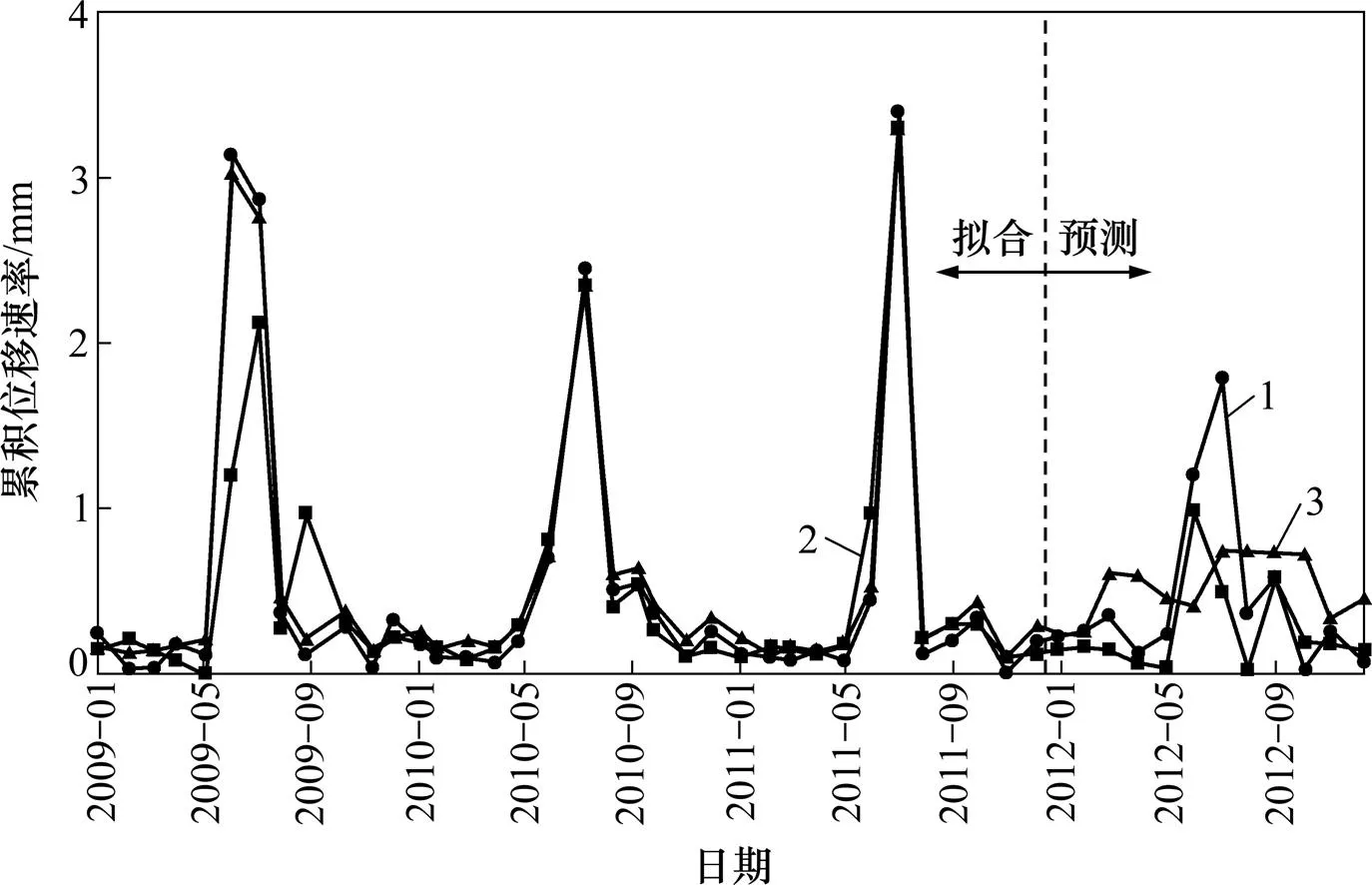
1—ZG118实测值；2—RS-PSO-SVR模型预测值；3—PSO-SVR模型预测值

对比分析2种模型的拟合结果与预测结果发现：2种模型对训练样本的拟合效果均较好，且未经过粗糙集属性约减的PSO-SVR模型的拟合效果优于约减后的RS-PSO-SVR模型的拟合结果，但对测试样本的预测结果明显比RS-PSO-SVR模型的预测结果差。该模型是基于10个影响因子构建的响应模型，从表1可以发现：10个影响因子间存在极强的耦合性和冗余性，当以该因子集作为SVR模型的输入特征向量对2009−2011年的训练样本进行拟合时，多因子的冗余叠加信息增强了SVR模型的拟合作用，引起了过拟合，当利用此训练好的模型对2012年的累积位移速率进行预测时造成精度极大降低，预测效果很差。而利用粗糙集约减后的核因子集作为输入特征向量训练的RS-PSO-SVR模型，既保证了影响滑坡变形的关键因素得以利用，又剔除了其他冗余及干扰信息的影响，因此，当利用该模型对测试样本进行预测时保证了较高的预测精度。表3所示为测试样本模型预测值及误差。利用均方差(SE)和判定系数(2)评价各模型的性能。通过计算得知，RS-PSO-SVR模型对测试数据预测的SE和2分别为0.163和0.520，而未经过粗糙集属性约减的PSO-SVR模型预测的SE和2分别为0.238和0.070，进一步说明RS-PSO-SVR模型具有较强的泛化预测能力。

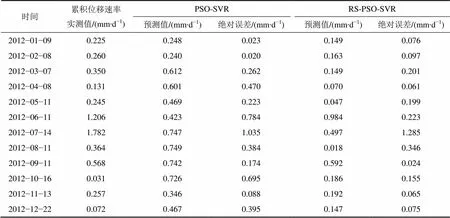
表3 测试样本模型预测值及误差

进一步分析RS-PSO-SVR模型的拟合预测曲线与实测曲线，发现二者变化趋势基本一致，2012年前样本拟合精度较高，尤其是2010年及2011年滑坡变形强烈、位移曲线出现陡增的5—8月份均拟合得较好。

2012−01—2012−12模型测试预测精度相对于样本训练累积位移速率有所降低，于2012−07—2012−08出现了较大误差，但预测趋势保证了与实测值的一致性。其原因主要是滑坡体各部分组成物质差异大，其岩土组成结构的复杂差异性导致滑坡复杂的非线性演化特征，3年的训练数据很难完全建立降雨及库水位与滑坡变形的响应关系，尤其在滑坡变形的突变处。在下一步研究中可以考虑建立动态更新预测模型，不断更新建模数据，增加建模的信息量，提高预测精度。

4 结论

1) 连续强降雨及库水位下降是导致滑坡强烈变形的主要影响因素。

2) 利用粗糙集理论进行属性约减，筛选出影响滑坡变形的核因子集，建立基于核因子集的粒子群优化支持向量回归预测模型，对滑坡累积位移速率进行预测，其预测结果与实测值变化趋势基本一致，测试样本的预测均方差和判定系数分别为0.163和0.520，证明该模型具有较强的泛化预测能力。

致谢：衷心感谢三峡库区地质灾害防治工作指挥部提供的数据支持！感谢曹雪莲老师在论文修改过程中提供的帮助！

[1] 李强, 李端有. 滑坡位移监测动态预报时间序列分析技术研究[J]. 长江科学院院报, 2005, 22(6): 16−19. LI Qiang, LI Duanyou. Research of dynamic prediction technique for landslide displacement monitoring[J]. Journal of Yangtze River Scientific Research Institute, 2005, 22(6): 16−19.

[2] 吴益平, 滕伟福, 李亚伟. 灰色−神经网络模型在滑坡变形预测中的应用[J]. 岩石力学与工程学报, 2007, 26(3): 632−636. WU Yiping, TENG Weifu, LI Yawei. Application of grey network model to landslide deformation prediction[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 632−636.

[3] 汤罗圣, 殷坤龙, 杜鹃. 跃型位移特征滑坡时间预测预报研究[J]. 地质科技情报, 2012, 31(4): 106−110. TANG Luosheng, YIN Kunlong, DU Juan. Time prediction for landslides with step-style displacement characteristics[J]. Geological Science and Technology Information, 2012, 31(4): 106−110.

[4] 马文涛. 基于灰色最小二乘支持向量机的边坡位移预测[J]. 岩土力学, 2010, 31(5): 1670−1674. Forecasting slope displacements based on grey least square support vector machines[J]. Rock and Soil Mechanics, 2010, 31(5): 1670−1674.

[5] 杜娟, 殷坤龙, 柴波. 基于诱发因素响应分析的滑坡位移预测模型研究[J]. 岩石力学与工程学报, 2009, 28(9): 1−7. DU Juan, YIN Kunlong, CHAI Bo. Study of displacement prediction model of landslide based on response analysis of inducing factors[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(9): 1−7.

[6] 彭令, 牛瑞卿, 叶润青, 等. 基于进化支持向量机的滑坡地下水位动态预测[J]. 中南大学学报(自然科学版), 2012, 43(12): 4788−4795. PENG Ling, NIU Ruiqing, YE Runqing, et al. Prediction of ground water level in landslides based on genetic-support vector machine[J]. Journal of Central South University (Science and Technology), 2012, 43(12): 4788−4795.

[7] Gorsevski P V, Jankowski P. Discerning landslide susceptibility using rough sets[J]. Computers, Environment and Urban Systems, 2008, 32(1): 53−65.

[8] 程温鸣, 彭令, 牛瑞卿. 基于粗糙集理论的滑坡易发性评价: 以三峡库区秭归县境内为例[J]. 中南大学学报(自然科学版), 2013, 44(3): 1083−1090. CHENG Wenming, PENG Ling, NIU Ruiqing. Landslide susceptibility assessment based on rough set theory: Taking Zigui County territory in Three Gorges Reservoir for example[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1083−1090.

[9] Pawlak Z. Rough sets[J].International Journal of Computer and Information Sciences, 1982, 11(5): 341−356.

[10] Vapnik W N. 统计学习理论的本质[M]. 张学工, 译. 北京: 清华大学出版社, 2000: 96−101. Vapnik W N. The nature of statistical learning theory[M]. ZHANG Xue-gong, trans. Beijing: Tsinghua University Press, 2000: 96−101.

[11] Kennedy J, Eberhart R C. Particle swarm optimization[C]//IEEE International Conference on Neural Networks. Piscataway:IEEE Service Center, 1995: 1942−1948.

[12] 王尚庆, 徐进军, 罗勉. 三峡库区白水河滑坡险情预警方法研究[J]. 武汉大学学报·信息科学版, 2009, 34(10): 1218−1221. WANG Shangqing, XU Jinjun, LUO Mian. Study on warning of dangerous state of Baishuihe landslide in Three Gorges Reservoir area[J]. Geomatics and Information Science of Wuhan University, 2009, 34(10): 1218−1221.

[13] 刘广润, 晏鄂川, 练操. 论滑坡分类[J]. 工程地质学报, 2002(4): 339−342. LIU Guangrun, YAN Echuang, LIAN Cao. Discussion on classification of landslide[J]. Journal of Engineering Geology, 2002(4): 339−342.

[14] Selim S Z, Ismail M A. K-means-type algorithms−a generalized convergence theorem and characterization of local optimality[J]. Ieee Transactions on Pattern Analysis And Machine Intelligence, 1984, 6(1): 81−87.

[15] Group of Logic, Institute of Mathematics, Warsaw University, Poland. Rough Set Exploration System[EB/OL]. [2015−01−19]. http://logic. mimuw.edu.pl/~rses.

(编辑 罗金花)

Prediction of landslide deformation based on rough sets and particle swarm optimization-support vector machine

ZHAO Yannan1, NIU Ruiqing1, PENG Ling2, CHENG Wenming3, 4

(1. Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China;2. China Geological Environment Monitoring Institute, Beijing 100081, China;3. Engineering Faculty, China University of Geosciences, Wuhan 430074, China;4. Command of Geological Hazard Control in Area of Three Gorges Reservoir, Yichang 443000, China)

The Baishuihe landslide in the Three Gorges Reservoir region was selected as an example. By analysing the response relationships between landslide deformation and influencing factors such as the rainfall and the reservoir water level, 10 initial influencing factors were reduced by using the rough set theory(RS). Then, the nuclear factor set influencing the landslide deformation was screened out. Finally, the particle swarm optimization (PSO) − support vector regression (SVR) model was established based on the nuclear factor set to predict landslide displacement rate. The results show that the test sample predictive mean absolute error, mean squared error and determination coefficient are 0.234 mm/d, 0.163 and 0.520, respectively. And the change trends are consistent between predicted results and the measured ones. The rough set theory is scientific and applicable in analysing landslide deformation characteristics and selecting key factors. The RS-PSO-SVR model is an effective method in landslide deformation predicting with high generalization ability.

landslide deformation prediction; rough sets; particle swarm optimization; support vector machine

10.11817/j.issn.1672-7207.2015.06.045

P 642.22

A

1672−7207(2015)06−2324−09

2014−10−17；

2014−12−20

国家重点基础研究发展规划(973计划)项目(2011CB710601)；国家高技术研究发展计划(863计划)项目(2012AA121303)；国土资源部三峡库区三期地质灾害防治重大科学研究项目(SXKY3-6-2)(Project (2011CB710601) supported by the National Program on Key Basic Research Project (973 Program); Project (2012AA121303) supported by the National High Technology Research and Development Program (863 Program); Project (SXKY3-6-2) supported by the Third Major Geological Disaster Prevention Research Project of Ministry of Land and Resources in the Three Gorges Reservoir Area)

牛瑞卿，博士，教授，从事3S与地质灾害研究；E-mail：rqniu@163.com