全纯曲线正规族分担超平面

郑晓杰， 刘晓俊

（上海理工大学 理学院，上海 200093）

1 问题的提出

在亚纯函数的值分布和正规族理论中，有一个著名的现象（Block原理），即一个在区域D⊂C 有性质 P 的亚纯函数族是正规的，如果这个性质 P 使得亚纯函数在整个复平面 C 上是常数。Zalcman发表了一个更精确的叙述(Zalcman引理和 Zalcman-Pang 引理[1-2]) 去判断亚纯函数族的正规性。在全纯曲线的例子中也存在一些类似的现象。

Chen等[3]证明了全纯曲线在强分担条件下的唯一性定理（定理1）。

定理1f和g是从 C 到 PN(C)的2个非常数全纯曲线，1 ≤j≤q，Hj是q个 在 PN(C)上处于一般位置的超平面，使得f(C)⊈Hj,g(C)⊈Hj，f(z)和g(z)分担Hj，1 ≤j≤q。如果q≥2N+3，则f=g。

这里的“分担”意味着不仅f(z)∈Hjg(z)∈Hj，而且要求在

Yang等[4]考虑了全纯曲线正规族理论的相应结果，得到定理2。

定理2F 是从D⊂C 到 PN(C)的全纯曲线族，Hj是q≥2N+1个在 PN(C)上处于一般位置的超平面，1 ≤j≤q。假定对于任意的f,g∈F,f(z)∈Hj⇔g(z)∈Hj，z∈D， 1 ≤j≤q，则 F在D上正规。

刘晓俊等[5]使用了一个导曲线的特殊曲线去替代g，证明了定理3。

定理3F 是从D⊂C 到 PN(C)的一族全纯映射。Hl={x∈ PN(C):x,αl=0}是 PN(C)上处于一般位置的超平面，其中， αl=(al0,···,alN)T和al0≠0,l=1,2,···,2N+1。假定对于任意的f∈F，满足下列条件：

a.若f(z)∈Hl，则 ∇f∈Hl,l=1,2,···,2N+1；

则 F 在D上正规。

Liu等[6]去除了上述定理在 P2(C)中超平面第一个系数的限制，证明了定理4。

定理4F 是从D⊂C 到 P2(C)的一族全纯映射 ，H0={w0=0}，Hl={x∈ P2(C):x,αl=0}≠H0是P2(C)上处于一般位置的超平面，其中，αl=(al0,al1,al2)T,l=1,2,3,4,5。假定对于任意的f∈F满足下列条件：

a.f(z)∈Hl当且仅当 ∇f∈Hl,l=1,2,3,4,5；

则 F 在D上正规。

由定理4可知，定理4的证明不能被推广到P3(C)的情况，因此，引出定理5。

定理5F 是从D⊂C到P3(C)的一族全纯映射，H0={w0=0}和Hl={x∈P3(C):x,αl=0}≠H0是P3(C)上处于一般位置的超平面，其中，αl=(αl,αl,αl,αl)T,0123l=1,2,3,4,5,6,7,8。假定对于任意的f∈F满足下列条件：

a.f(z)∈Hl当且仅当 ∇f∈Hl,l=1,2,3,4,5,6,7,8；

则 F在D上正规。

在证明定理5之前，先说明一些概念。

一般地，D是 C 上一个区域，H0={w0=0}总是表示第一坐标超平面。fn(z)⇒f(z)，z∈D表示{fn}在D的紧致集上关于 PN(C)上的Fubini-Study度量 一 致 收 敛 于f。 对 于 在D上 的 全 纯 曲 线f(z)，f(z)在点z处的球面导数定义为

2 重要概念

首先介绍 PN(C)的一些定义和概念。

PN(C)=CN+1{0}/∼为N维复射影空间，对于x=(x0,x1,···,xN)，y=(y0,y1,···,yN)∈ PN(C)=CN+1{0}，x∼y当 且仅当存在 λ ∈C ，使得(x0,x1,···,xN)=λ(y0,y1,···,yN)。(x0,x1,···,xN)的等价类 定义为[x0:x1:···:xN]，PN(C)={x=[x0:x1:···:xN]:x=(x0,x1,···,xN)∈ CN+1{0}}。H1,H2,···,Hq为 PN(C)上的超平面 ， 它 们 定 义 为Hℓ={x∈ PN(C):〈x,αℓ〉=aℓ0x0+aℓ1x1+···+aℓNxN=0}， 其 中 ， 非 零 向 量 αℓ=(aℓ0,aℓ1,···,aℓN)T,ℓ=1,2,···，q。

定义1超平面H1,H2,···,Hq处于一般位置，如果对于任意的单射 φ :{0,1,2,···,N}→ {1,2,···,q}，向量组 αφ(0),···,αφ(N)是线性无关的。

其次，令f:D→PN(C)为全纯映射，U为D上一个开集。对于任何全纯映射f:U→CN+1，使得P(f(z))≡f(z)，z∈U，称f为在U上的一个代表，其中， P :CN+1{0}→PN(C)为标准商映射。

定义2对于D的任意开子集U，若f0,f1,···,fN是U上没有公共零点的全纯函数，则称f=(f0,f1,···,fN)为f在U上的简约表示。

Hℓ={x∈PN(C):x,α=0}为一个超平面，定义一般地，只考虑标准超平面，使得 ∥H∥=1。

对于全纯映射f的任意简约表示f，定义全纯函数

根据文献[7]中定义的导曲线，可得定义3。

定义3设f是从D到 PN(C)的全纯映射，f=(f0,f1,···,fN)是f在D上的任意简约代表，fµ(z)≢ 0，µ ∈ {0,1,···,N}，则有

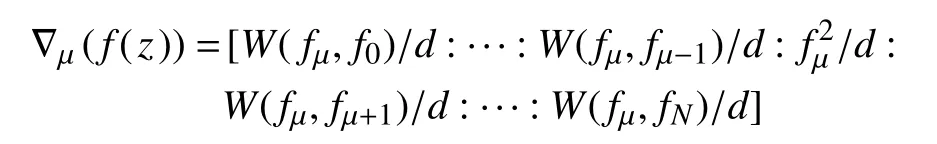
被称为f的第 µ个导全纯映射，其中，d(z)为全纯函数，使得/d和W(fµ,fi)/d没有公共零点，i=0,1,···,N，i≠ µ。

为了简单起见， ∇µf写为 ∇f，显然， ∇µf的定义不依赖于f的简约表示的选择。

3 预备定理

在给出定理5的证明之前，需要由Aladro等[8]证明的从区域 Ω ⊆C 到 PN(C)的全纯映射的Zalcman引理。

引 理1[8]F 是 从 双 曲 区 域 Ω ⊂C 到 PN(C)的一族全纯映射，若 F 在 Ω 上不正规当且仅当存在数列 {fn}⊂F,{zn}⊂Ω，zn→z0∈Ω，和 {ρn},ρn>0，ρn→0，使得

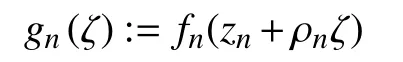
在 C 的紧致集上一致收敛到一个非常数全纯映射g，g从 C 映到 PN(C)。

由Nevanlina理论中退化的第二基本定理得到引理2。

引理2[9]设f:C→PN(C)是一个全纯映射，H1,···,Hq(q≥ 2N+1)是 PN(C)上处于一般位置的超平面。若对于j=1,···,q，f(C)不是含于Hj中，就是不含于Hj，则f是常数。

引理3[9]设f0,f1,···,fn+1是处处不为0的整函数，且

考虑划分

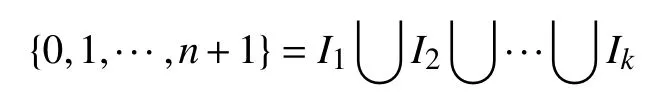
使得i和j在同一个类Iℓ当且仅当fi=cijfj，cij为某个非零常数，则对于任意的Iℓ，可得

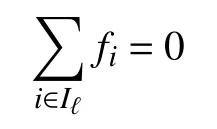
引理4[10]若f(z)和 ϕν(z)(ν=1,2,3)是有限平面上的亚纯函数，使得

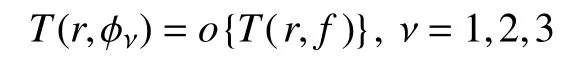
则有

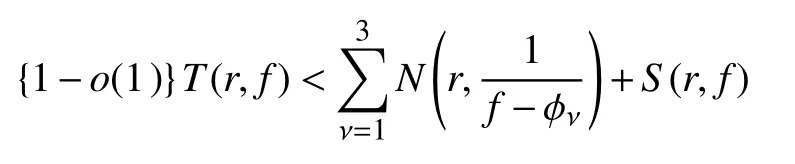
其中，S(r,f)=o{T(r,f)}，r→ ∞。

引理5[6]设g=[g0:···:gN]:C → PN(C)是有穷级的全纯曲线，g0(ζ)≢ 0，其中，N≥2，N是整数。Hℓ={x∈PN(C):x,αℓ=0}是 PN(C)上处于一般位置的超平面，它们的首项系数aℓ0非零，l=1,2,···,2N+1。设 g (ζ)=(g0,g1,···,gN)(ζ)是g的任意简约代表，定义

假 定Gℓ(ζ)≠0，ζ∈C 和G′ℓ(ζ)≠ 0，ζ∈ C ， 则g线性退化。

4 定理5的证明

假定 F 在D上不正规，则由引理1可知，存在zn→z0∈D，正点列 ρn→0和全纯映射列fn∈F，使得

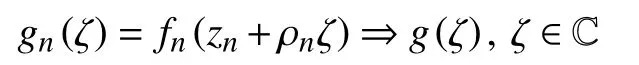
其中，g是 C上的有穷级的非常数全纯映射。

设g(ζ)=(g0,g1,g2,g3)(ζ)是g的简约代表。因为，Hℓ处于一般位置，1 ≤ℓ≤8，不失一般性，可以假设H1,H2,H3,H4和H5的首项系数不为0。

情形1g是非线性退化。

情形2g是线性退化。

假设g0,g1,g2是线性非退化。因为，Gℓ≡0或者Gℓ≠0,ℓ=1,2,3,4,5，而由引理5可知，有g0≠0和g是一个全纯映射，则Gℓ在 C上全纯。

因为， ρGℓ≤1,1≤ℓ≤5，则

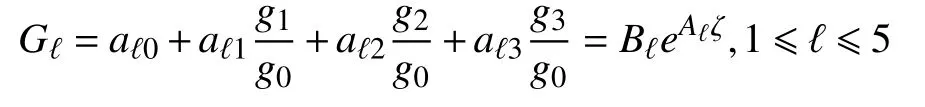
特别地，当Gℓ≡0，Bℓ=0，∀j1,j2,j3,j4∈{1,2,3,4,5}，不失一般性，设j1=1,j2=2,j3=3,j4=4，令k1B1eA1ζ +k2B2eA2ζ+k3B3eA3ζ+k4B4eA4ζ=0， 其中，k1,k2,k3和k4为常数。

令

因 为 ， d etA≠0， 则 令(k1,k2,k3,k4)T=A−1(b1,b2,b3,b4)T，它是一个非零向量，则B1eA1ζ,B2eA2ζ,B3eA3ζ,B4eA4ζ是线性退化。

断言存在单射 σ :{1,2,3}→{1,2,3,4}，使得Bσ(1)eAσ(1)ζ,Bσ(2)eAσ(2)ζ,Bσ(3)eAσ(3)ζ线性非退化。

证明不失一般性，可以假设存在 ℓ1,ℓ2,ℓ3，使得B4eA4ζ = ℓ1B1eA1ζ+ℓ2B2eA2ζ+ℓ3B3eA3ζ。因为，

则

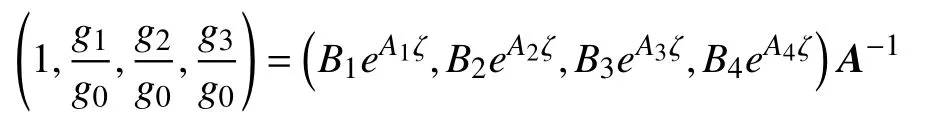
所以，可令

若r(C)≤2，那意味着方程组

有非零解，则存在不全为0的数q0,q1,q2，使得

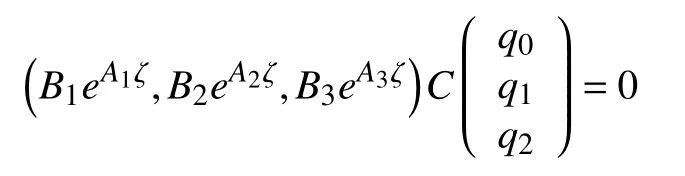
即

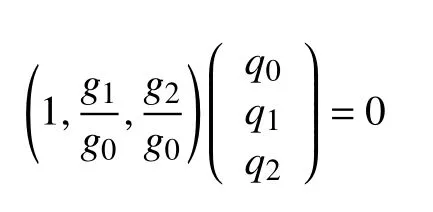
如果B1eA1ζ,B2eA2ζ,B3eA3ζ是线性退化，则存在不全为0的c0,c1,c2，使得

由式(1)可得

所以，B1eA1ζ,B2eA2ζ,B3eA3ζ是线性非退化，意味 着A1,A2,A3互 不 相 同 。 因 为 ，Hℓ,1≤ℓ≤5是P3(C)上处于一般位置的超平面，则A1,A2,A3,A4,A5中任意4个存在3个不同。

若存在l∈{1,2,3,4,5}，使得Bl=0，不失一般性，令B5=0，则Bi≠0,i=1,2,3,4。

若A1,A2,A3互不相同，则A4等于A1,A2,A3中一个，不妨设A4=A1。类似地，A5等于A1,A2,A3中一个，不妨设A5=A2。

所以，在A1,A2,A4,A5中不可能存在3个相同，矛盾，则g0,g1,g2线性退化。

因此，存在不全为0的p0,p1,p2，使得p0g0+p1g1+p2g2=0。

a.p2≠ 0，则可被g0,g1线性表示。

所以，存在常数k1,k2,l1,l2，使得g2=k1g0+k2g1,g3= ℓ1g0+ℓ2g1，则

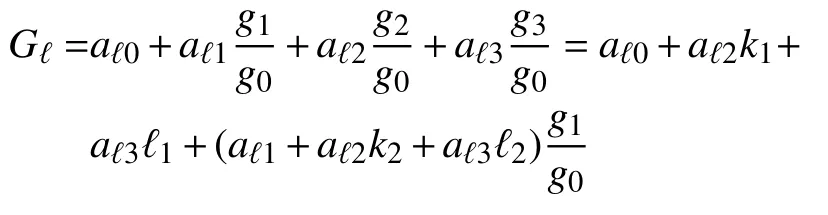
因为， α1,α2,α3,α4线性无关，则存在 ℓ ∈{1,2,3,4}，使得aℓ1+aℓ2k2+aℓ3ℓ2≠ 0。

不失一般性，由引理2可假设H6的首项系数不为0，即a60≠0。如果H7的第一个系数仍不为0，即a70≠0，有g不 取H7或者g(C)含于H7。

因为，α6=(0,a61,a62,a63)T，所以，〈g,α6〉的所有零点是重级的。因此，

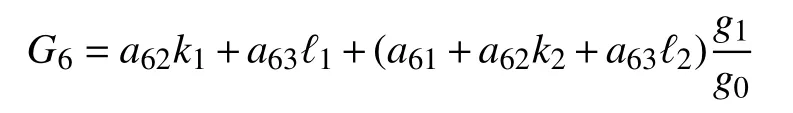
的所有零点是重级的。

如果对于任意 ζ ∈C， 〈g,α6〉≠ 0或 ≡ 0。由引理2可得g是常数曲线，矛盾。

则存在ζ0∈ C，使得〈g,α6(ζ0)〉=0和〈g,α6(ζ)〉≢ 0，这意味着

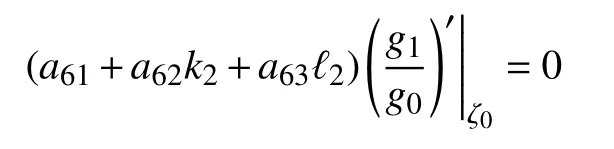
矛盾。

因此，H7的第一个系数为零，即a70=0。类似地，有 〈g,αℓ〉的所有零点为重级零点，即

的所有零点是重级零点。

若 对于 任 意的 ζ ∈ C,〈g,αℓ〉≠ 0或 ≡ 0， ℓ =6,7。由引理2，g是 常数曲线，矛盾。所以，存在 ζ0∈ C，ℓ=6或7，使得〈g,αℓ(ζ0)〉=0和〈g,αℓ(ζ)〉≢ 0。这意味着

矛盾。

b.p2= 0，则p0,p1不全为0。

(a)p0≠ 0，矛盾；

(b)p0= 0，则p1≠0，这意味着g1≡ 0，则0，矛盾。

因此， F 在D上 正规，所以，定理5得证。