初中数学教学中的数形结合刍议

陈强

【内容摘要】初中数学教学中涉及到许多与图形相关的学习内容，许多几何图形与数据相互关系都难以直接用叙述性语言来表达。因此“数形结合”的方法能够有效的将无法用叙述性语言表达清楚的意思表达出来，更加易于学生对题目的理解与求解。

【关键词】初中数学 教学 数形结合 应用 刍议

数学学习在许多时候都是一些相对非常抽象的数字、图形、公式等，虽然有着非常重要的实用价值然而理解这些偏抽象性的知识时，仍然会面临许多难点和疑惑。当前社会对各种知识需求水平的增加使学生们面临了更高水平的学习任务，只有利用有效的教学方法加强每一项数学知识的掌握水平才能满足社会的需求。

一、数形结合思想的概念及在初中数学教学中的意义

数形结合顾名思义就是将无法用语言理顺的数学知识利用数字与图形结合的方式表现出来，使学生能够更直观的理解每一个数学因子之间的关联，实现数和形的有机结合，提高教学效果。由于初中数学教学中许多抽象数学理论及规律、定理等的出现，为学生理解数学知识带来了较大的难度，因此许多数学教师都选择以数形结合的方式来弱化数学知识的抽象性，通过数字与图形的转化或者以图形将数字用一定规律联系起来的方式来提高教学效果，使学生能够在更加直观的说明中实现对知识的理解。

二、数形结合在初中数学教学中的应用策略

1.思想导入

传统的数学教学方法上，数形结合无疑是一种非常有效的教学手段，然而理解数形结合的思想需要有一个逐渐接受的过程，对于学生而言如果一下子将原本的教学模式撇开而直接加入数形结合教学手段，学生不仅无法适应甚至更无法理解，对教学效果提高反而会起到相反的作用。教师只有关注数形结合思想的导入方法才能获得预期的教学提升效果。

例如，对正数负数概念的解释，需要首先对0和正数进行思想认识的强化，然后画一条数轴标示出0和若干个正数，当学生适应了由数字到数轴的转变之后，再加入负数的概念，这样即能使学生更加自然的理解负数的概念，还能够有效导入数形结合的思想，简化了数学概念的理解过程，提高了教学效果。

2.思路展开

初中数学中许多问题需要拓展思路才能得到解答，而每一种不同的问题思路拓展的方式又千差万别，所以让学生掌握数学问题思路拓展的方法才能有效提高学生解答问题的能力。

以方程学习为例，每种类型的方程式最有着基本相同的特点，因此只需要将思路拓展的方向教授给学生，他们就能够掌握有效解决问题的方法。数轴仍然是方程相关的问题寻求答案的最佳方式之一，一般比较适用于多元方程组，每一个方程中两个未知数的关系都可以用一条以x为横坐标、以y为纵坐标的斜线表示，而两个方程组的解就是两条斜线交叉点x、y值，这样就将抽象的方程组转变为图形化解决了问题，并且对于任何一个二元方程组都能够以些思路做来寻求解决方法。

3.思想升华

数形结合的思想不仅能够对简单的数学问题进行有效解决，还能够对复杂的数学函数关系进行图形化处理，从而使学生学习难度下降，有效提高教学效果。函数关系的理解无法通过抽象的思维想象来完成，因此利用数形结合是非常重要的教学手段。在数学知识中函数本身就通过函数图像来说明的某两个或几个数据之间的关系，单纯运用函数图像对函数关系的说明虽然比较易于实现，然而在许多比较复杂的函数问题解答时，就要对数形结合的思想进行创造性处理才能满足教学要求。

三、数形结合思想应用实例分析

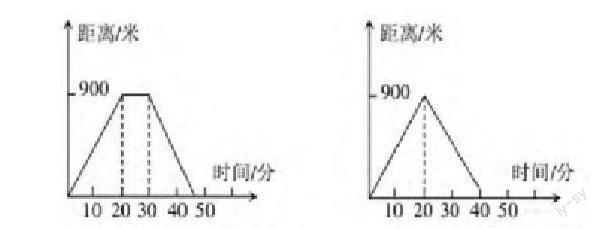
例一：A与B两人他们即是同学也是朋友，某一天二人决定去距离他们家均为900米远的公园门口玩，由于两人忘记约好出发和集合的时间，因此二人在第二天去往小公园门口的路上没有相遇，其中A走了20分钟后到公园门口，然后坐下等了十分钟不见B来故返回家中，而B同样是走了20分钟到达公园门口，由于未见A的身影所以用15分钟快速返回家中。请问：你能将A和B离家时间与离家距离的关系分别表示出来吗？

这是一个运用数形结合思想就变得极为简单的问题，如果学生一直基于思索离家时间和离家距离之间的数据关系，是无论如何也难以得出直观的答案的。教师应当引导学生对于这种距离与时间变化不规律的数学关系要选择图形来解决问题。以时间为横轴、距离为纵轴，不难得出二人随时间变化和各自离家距离之间的关系，如下图：

例二：已知平行四边形的两条临边分别长10、15，两条边的夹角为60°，求平行四边形的面积。

这也是一个比较简单的几何数学题，但如果不运用数形结合的思想仅仅靠学生的思索难以求得以某条边为底的平行四边形的高，所以也难以计算出它的面积，对于几何图形的问题教师要为学生树立起用图形来寻找解决方法的思路，将平行四边形画到纸上，然后将所有的已知条件标明，就可以很直观的看到通过两边和夹角就可以计算出平行四边形的高，从而求出它的面积。

四、结语

数学教学中无论是否是几何图形问题，都需要将许多特殊问题进行数形结合的转化，才能将复杂的问题简单化，尽快求解出正确答案，而数形结合思想的应用不仅能够提高教学效果，更能够实现学生学习能力的提高，所以在数学教学中有着极大的实践意义。

（作者单位：江西省赣州市第二中学）