基于密度的孤立点检测算法改进研究

吕奔，高茂庭

（上海海事大学信息工程学院，上海 201306）

基于密度的孤立点检测算法改进研究

吕奔，高茂庭

（上海海事大学信息工程学院，上海 201306）

0　引言

孤立点检测是数据挖掘领域的一个重要分支，在数据集中，孤立点数据通常被定义为与其他数据对象有着明显差异的数据。Hawkins在20世纪80年代给出了一个比较接近孤立点本质的定义［1］：“孤立点与其他点如此不同，以至于让人们怀疑它是由另一个不同的机制产生的。”孤立点检测在实际生活中有很多重要的应用，如网络入侵检测、金融欺诈检测、运动员比赛分析、医学领域中发现病人对新的治疗方案的异常反应等［2］。

为了有效地刻划孤立点的孤立程度，Breunig等人提出了局部异常因子（LOF，Local Outlier Factor）的概念与算法［3］，LOF是一种基于密度的孤立点检测算法，它的优点在于考察的是数据对象与其周围邻居相比的孤立程度，而不是从全局的角度来考虑数据的孤立特性。LOF算法不是去界定哪些数据对象是孤立点或者哪些数据对象不是孤立点，而是去量化地描述数据对象的孤立程度，通过赋予每个数据对象一个表示它孤立程度的指标，并以此作为对孤立点进行检测的依据。数据对象的LOF值越大，则它是孤立点的可能性就越大。LOF算法只需要确定最近邻的个数k，不需要对数据获取过多的先验知识［4］。

然而，在计算LOF的时候需要对全部数据依次计算，没有针对性，计算复杂度很大。为了解决LOF时间复杂度较大的问题，本文利用DBSCAN聚类算法具有处理速度快、有效处理噪声点的特点［5］，将DBSCAN引入进行数据的预处理，从而提出一种改进的基于密度的LOF孤立点检测算法DBLOF（Density Based Local Outlier Factor）。DBLOF算法首先运用DBSCAN进行数据异常点的筛选，减少在孤立点检测阶段的处理数据，使得检测数据更有针对性，然后，在计算LOF时，尽可能使用已知信息对邻近数据对象进行优化操作，从而提高算法的执行效率。

1　DBLOF算法

传统LOF算法的核心思想是给每一个数据对象赋予一个衡量该数据对象孤立程度的因子，这个孤立因子值并不是明确判定哪些数据对象是孤立点哪些不是孤立点，它只是用来反映数据对象是否分布在较为集中的区域中。

为使表达更清楚，在介绍LOF算法之前，先介绍几个相关的概念，设D为数据对象集，p为D中的数据对象。

p的k距离：定义为对象p与离它第k近的对象q之间的距离，记为k-dist（p）。这样的对象可能只有一个也可能有多个，若p与q之间的距离用d（p，q）表示，则对象q需要满足的条件为：

①至少存在k个对象q'∈D-｛p｝，满足d（p，q'）≤d （p，q）。

②至多存在k-1个对象q'∈D-｛p｝，满足d（p，q'）≤d（p，q）。

p的k距离邻域：是指所有与对象p的距离不大于k-dist（p）的数据对象的集合，即：

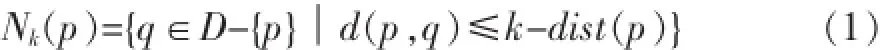
p与q的可达距离：指对象 p到对象 q的距离和q 的k距离两者中的最大值，其中对象q∈Nk（p），即：

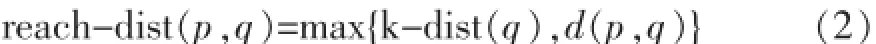
p的局部可达密度：定义为对象p与它的Nk（p）内各对象的平均可达距离的倒数，按式（3）计算：

局部异常因子（LOF）：表征数据对象p在k距离邻域内的孤立（异常）程度，按式（4）计算：

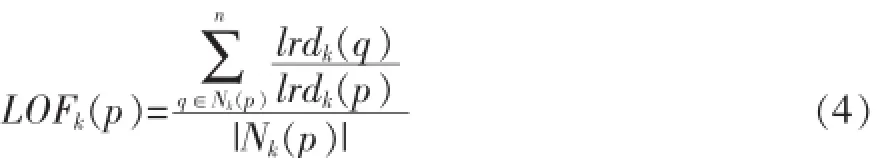
LOF算法的实现步骤如下［6］：

①计算数据对象p的k距离k-dist（p）。

②计算p的k距离邻域Nk（p）和可达距离。

③计算数据元素p的局部可达密度lrdk（p）。

④计算p的局部异常因子LOF。

LOF值越大，该对象越有可能就是孤立点，LOF值越小，该对象p越不可能是孤立点［7］。

LOF算法的缺点是计算复杂度大，根据以上LOF的计算过程，主要是由于第二步计算过程复杂。在p的k距离邻域Nk（p）内，要计算该邻域内每个对象的可达距离，包括在p的k距离邻域Nk（p）计算所有对象的k-dist和p与每个邻居对象之间的距离，每种情况下选出最大值。由于每个对象都至少有k个最近邻数据对象，因此要得到所有对象的局部可达距离至少要做kn次比较，n越大的话，计算和比较的次数越大，时间就越长。为此，需要在邻域查询操作中进行优化［8］。

然而，孤立点只是整个数据集的一小部分，可以用DBSCAN算法进行预处理，去除不包含孤立点的类，以减少计算复杂度。

局部异常因子LOF［9］用于表征数据集中每个数据对象的异常程度，并且这种异常是局部的，与所求数据对象的邻域分布有关。但是LOF算法并没有将这一思想应用到计算局部异常因子的实际操作中。在LOF算法的邻域查询过程中，一个对象p的邻域查询信息仅仅用于处理对象自己，在该邻域查询结束后这些信息就被丢弃。实际操作中，这些信息对于Nk（p）中所有对象的邻域查询都是非常有用的，为了说明这点，以二维平面的数据点为例，假设参数k的取值为4，圆1和圆3以p为圆心，半径分别为k-dist（p）和3×k-dist（p），圆2是以对象d为圆心，半径为2×k-dist（p），如图1所示。

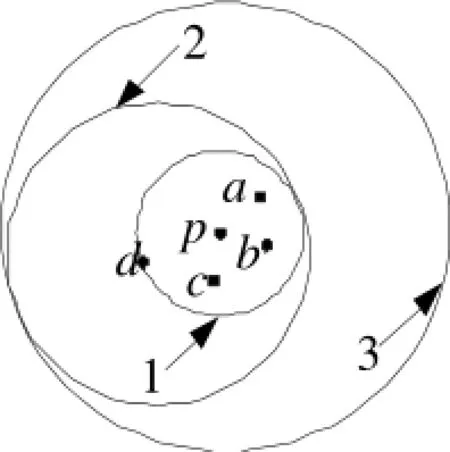
图1　邻域优化查询示意图

图1中，Nk（p）中至少包含4个对象，Nk（p）=｛a，b，c，d｝。按照LOF算法，获得Nk（p）与相关的距离之后，对象p的邻域查询过程结束，应该选取另外一个点比如a再次进行邻域查询。实际上，对象a，b，c，d的邻域查询范围只需要在圆3的区域内进行［10］，不必在整个数据集中查询。不难想到，要对a进行邻域查询，目的是找到在a邻域附近k个对象就可以，因为a在圆1中，而圆1中至少包含了k+1的对象（含p对象）。如果以a为圆心，2×k-dist（p）为半径的范围内已经包含圆1的区域了，这就可以确保该范围内至少包含k+1个对象。考虑边界对象的情况，可以确定以p为圆心，3×k-dist（p）为半径构造出的圆3就是适合Nk（p）中所有对象的邻域查询范围，而不必在整个数据集中进行查询，显著地减少了计算量。

优化后邻域查询步骤如下：

①从数据集中选择一个尚未处理的对象p，在数据集D内进行查询，获得k-dist（p）、Nk（p）和所有其他对象与p之间的距离。

②在Nk（p）内选取与p的距离最小且没有处理过的对象q，再以3×k-dist（p）为半径的范围内进行查询。然后从与p的距离次小且没有处理过的对象循环上述邻域查询过程，直到满足查询区域内对象数量超过指定阈值。

③若数据集中还有未处理的对象，则转到①，继续下一轮循环，否则，结束循环，优化查询完成。

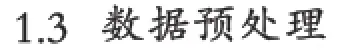
孤立点的数目比一般数据的数目要少很多，所以计算数据集中绝大多数非孤立点的LOF是低效的，为了提高效率，通过减少用于计算的数据集的大小来减少不必要的计算。DBSCAN算法具有聚类速度快、发现任意形状类簇和有效处理噪声的优点［11］，本文选取DBSCAN算法进行数据预处理。但是DBSCAN算法的聚类结果受参数ε和MinPts影响较大［12］，为了减少孤立点被聚到簇中的可能性，利用不同组参数ε和MinPts的设置得到聚类模型来过滤数据对象，然后集成得到结果：只有数据对象在每组参数ε和MinPts都被聚集到某个簇时，才认为该数据对象是被聚集的簇对象，否则被认为是初步异常数据集，将其加入到异常数据集中。预处理过程如图2所示。

图2　数据预处理过程

预处理的策略是：首先确定DBSCAN参数，例如MinPts的大小设置为数据集对象总数的5%左右，ε可以根据排序的k-dist图确定。然后保持参数ε不变，以经验参数MinPts为中心选取MinPts-i，类似地，保持MinPts不变，以ε为中心选取ε-j。预处理的过程如下

①DBSCAN算法通过检查数据集中每个对象的ε邻域来寻找聚类，邻域查询采用1.2节中的邻域优化查询算法，使用不同组参数（ε-i，MinPts-j）分别对数据进行聚类，其中i和j不同时为0。每组的聚类按照②和③进行。

②如果一个对象p的ε邻域包含多余MinPts个对象，则创建以p为核心对象的新簇。反复寻找这些核心对象直接密度可达的对象，这一个过程可能会涉及到一些密度可达簇的合并。

③当没有新的对象可以添加到任何簇时，则聚类算法结束。

④多组聚类结束后会得到多组簇，只有数据对象在每组参数下都被聚集到某个簇时，才认为该对象是被聚集的簇对象，否则就被认为是初步异常数据，将其加入到初步异常数据集中。

通过以上分析，本文对基于密度的孤立点检测算法做了一些改进，基本思想是：首先通过DBSCAN算法对数据集进行预处理，处理过程中使用不同组参数来避免位于簇边缘的孤立点错剪（计算ε-邻域的时候使用邻域查询优化算法），得到初步异常数据集。然后利用LOF算法中计算局部异常因子的方法计算初步异常数据集中数据的孤立程度。最后根据要求选出孤立程度最大的前n个数据点作为孤立点。

DBLOF算法的描述如下：

输入：数据集D，参数k，ε，MinPts，n

输出：数据集D的孤立点集合

①数据初始化。分类数据数值化，连续型数据离散化。

②数据预处理。在DBSCAN算法中，利用不同组ε和MinPts参数对数据集进行聚类，用邻域查询优化思想来查询数据集中每个对象的ε-邻域。当且仅当数据对象在每组参数下都被聚集时，才认为该对象是被聚集的簇对象，将其去除。否则认为是非簇对象，将其加入到初步异常数据集。

③在初步异常数据集中选择一个没有被处理过的对象。若MinPts＞k，则在ε-邻域寻找该对象的k距离邻域，否则在整个数据集中寻找k距离邻域。

④计算各个数据点的局部可达密度和局部异常因子。

⑤输出局部异常因子的最大的n个点，将其加入到孤立点集中。

2　实验与分析

为了验证本文提出的DBLOF算法在孤立点检测中的有效性，将其与传统的LOF孤立点检测算法进行对比。

实验环境为：Intel Pentium CPU主频2.2GHz，内存2GB，操作系统为 Windows XP，工具为 MATLAB 7.12.0。

实验所用的数据集为随机生成的二维点集，该数据集包含148个数据点，其中有两个簇集和6个明显偏离簇的异常点。数据集的可视化显示见图3。

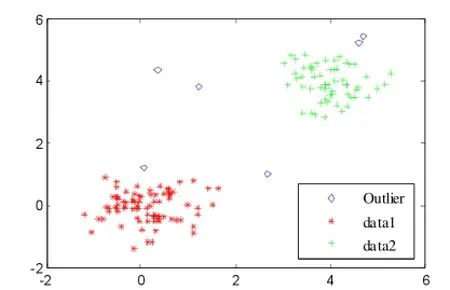
图3　数据集和孤立点分布图

为了更直观的展示DBLOF算法和LOF算法的检测结果，本文从两个方面进行评价：

首先，为了衡量算法的检测性能，使用精确度进行衡量。

其次，从实验运行的时间上进行对比，以此证明DBLOF算法的计算复杂度更低。

实验参数的设定：参数ε取值在0.4～0.6之间；因为k和MinPts都是表示数据点个数，且含义相近，所以参数k和MinPts的取值设为相同；又因为数据集中有6条真实的孤立点（孤立点的编号依次为51、101、102、 136、146、148），所以参数n从6开始选取，且每次加1，直到选取的前n个最大的孤立点中全部包含6条真实的孤立点。

实验参数ε=0.6，k和MinPts均为4，实验结果如图4和图5所示，从图中看出要检测出全部6个孤立点，LOF算法的n为11，DBLOF算法的n为7。具体的实验结果见表1和表2。

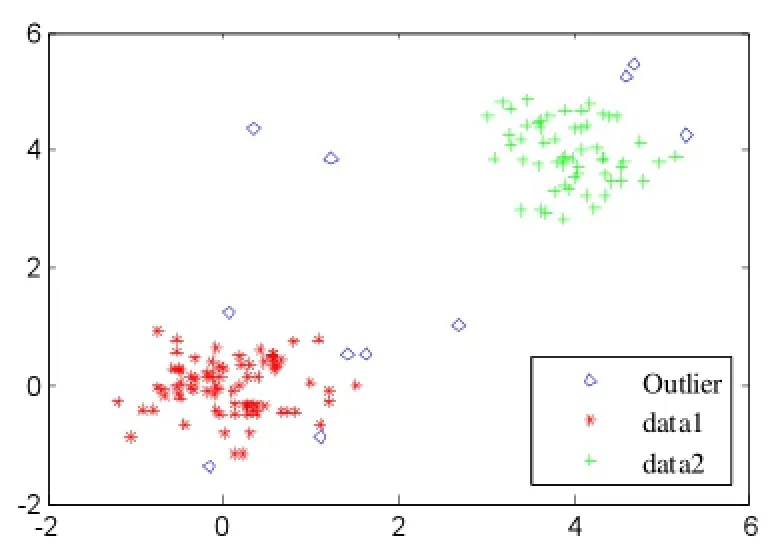
图4　LOF算法检测结果

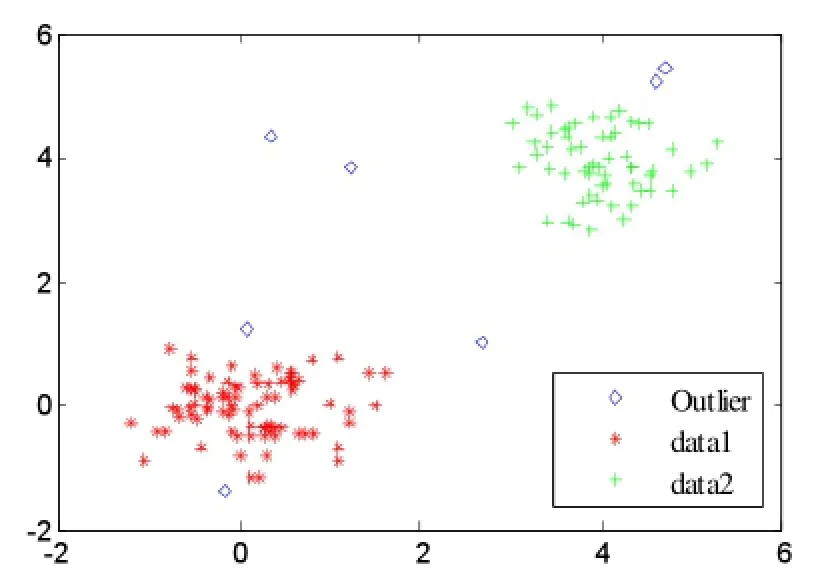
图5　DBLOF算法检测结果

根据图4、图5的检测结果，DBLOF算法检测的7个孤立点中包含了全部6个真实的孤立点，LOF算法检测的11个孤立点中也包含了全部的6个孤立点。但是，对比两张表可以看到，在检测出最后一个编号为136的孤立点时，LOF算法是在第11个才检测出来，DBLOF算法在第7个就可以检测到。因此，DBLOF算法相比LOF算法只需要更短的计算过程，也就是说DBLOF算法比LOF算法降低了孤立点检测的计算复杂度。从图6的时间对比图中，可以看出DBLOF算法的运行效率明显优于LOF算法。

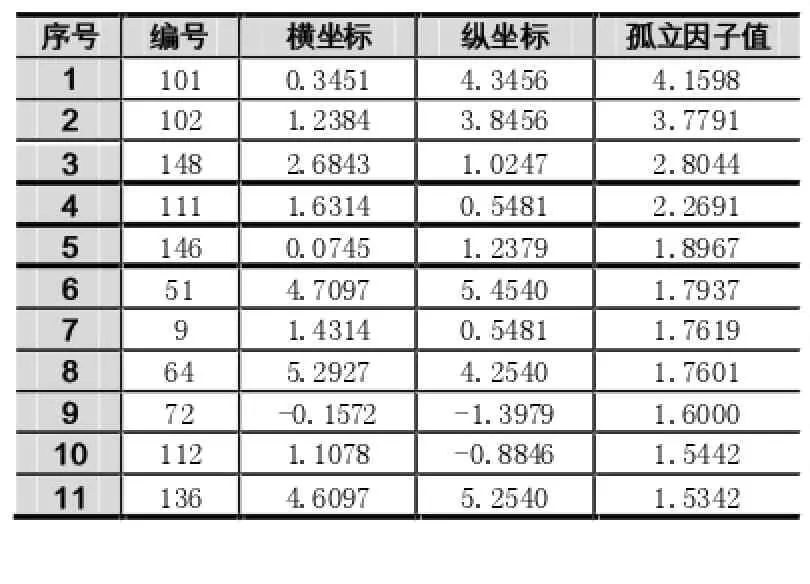
表1　LOF算法的检测顺序

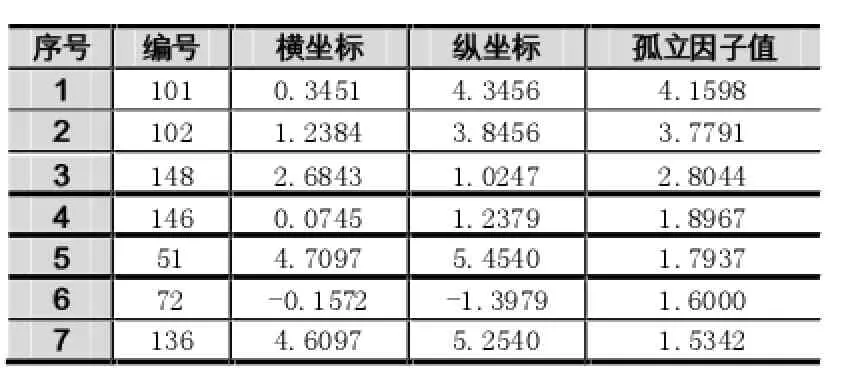
表2　DBLOF算法的检测顺序

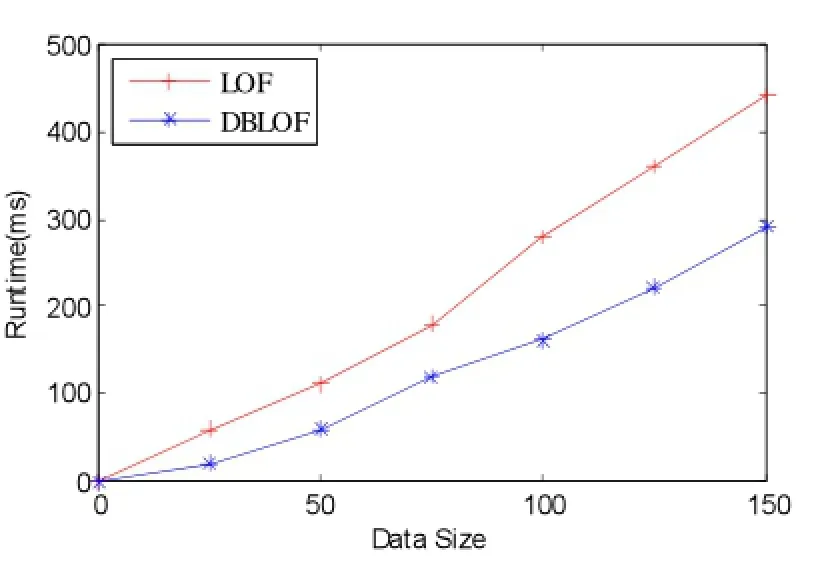
图6　DBLOF和LOF运行时间对比图

在精确度方面，如果n选择为7的话，DBLOF算法的准确率为100%，LOF算法的准确率仅为67%（4/6），DBLOF算法的准确率比LOF算法的准确率要高。

3　结语

本文在基于密度的孤立点检测LOF算法的基础上提出了DBLOF算法。改进算法利用邻域优化查询方法降低邻域查询时计算复杂度，并且通过聚类DBSCAN算法对数据集进行预处理，得到初步异常数据集，使得孤立点的检测对象更具有针对性。在采用二维点集的实验中，改进算法取得了较好的检测效果。但是在改进的算法中，参数k和MinPts的关系以及取值，直接影响到临近点的查询范围。因此，下一步将研究参数之间的关系对运行时间和精确度的影响，期望找出自动提供合理参数的方法。

［1］Dantong Yu，Gholamhosein Sheikholeslami，Aidong Zhang.FindOut：Finding Outliers in Very Large Datasets［J］.Knowledge and Information Systems，2002（4）

［2］范洁.数据挖掘中孤立点检测算法的研究［D］.中南大学，2009.

［3］Dutta H，Giannella C，Borne K，et al.Distributed top-k Outlier Detection in Astronomy Catalogs Using the Demac System［C］.Proc of 7th SIAM International Conference on Data Mining，2007.

［4］胡彩平，秦小麟.一种基于密度的局部离群点检测算法DLOF［J］.计算机研究与发展，2010，12：2110-2116.

［5］姜晗，贾泂.基于聚类的孤立点检测算法［J］.计算机与现代化，2007，11：37-39.

［6］张卫旭，尉宇.基于密度的局部离群点检测算法［J］.计算机与数字程，2010，10：11-14.

［7］鄢团军，刘勇.孤立点检测算法与应用［J］.三峡大学学报（自然科学版），2009，01：98-103.

［8］刘大任，孙焕良，牛志成等.一种新的基于密度的聚类与孤立点检测算法［J］.沈阳建筑大学学报（自然科学版），2006，01：149-153.

［9］李健，阎保平，李俊.基于记忆效应的局部异常检测算法［J］.计算机工程，2008，34（12）：4-6.

［10］李健，阎保平，李俊.MELOF算法的理论分析与拓展［J］.计算机工程，2009，19：94-96

［11］冯少荣，肖文俊.基于密度的DBSCAN聚类算法的研究及应用［J］.计算机工程与应用，2007，43（20）：216-221.

［12］冯少荣，肖文俊.DBSCAN聚类算法的研究与改进［J］.中国矿业大学学报，2008，01：105-111.

Outlier Detection；LOF；DBSCAN；Clustering；Data Mining

Improvement of Detection Algorithm Density-Based Local Outlier

LV Ben，GAO Mao-ting
（College of Information Engineering，Shanghai Maritime University，Shanghai 201306）

国家自然科学基金项目（No.61202022）、上海海事大学科研项目

1007-1423（2015）17-0062-06

10.3969/j.issn.1007-1423.2015.17.014

吕奔（1989-），男，江苏徐州人，硕士研究生，研究方向为为数据挖掘

2015-04-27

2015-06-25

针对基于密度的孤立点检测算法LOF时间复杂度高的问题，通过优化数据对象邻域查询过程，提出一种两阶段的改进算法DBLOF，先采用DBSCAN聚类算法对数据集进行预处理，去除大部分的非孤立点，得到可能异常数据集，然后再利用LOF算法计算可能异常数据集中对象的局部异常因子并以此找出真正的孤立点。实验结果表明，改进算法能实现有效的局部孤立点检测，并能够降低算法时间复杂度。

孤立点检测；LOF；DBSCAN；聚类；数据挖掘

高茂庭（1963-），男，江西九江人，博士，教授，系统分析员，CCF高级会员，研究方向为智能信息处理、数据库与信息系统

For the high time complexity of the density-based outlier detecting algorithm（LOF algorithms），proposes an improved algorithm DBLOF with two-stage by optimizing the neighborhood query operation of adjacent objects for each data object.Firstly，clustering algorithm DBSCAN is taken to preprocess the dataset and remove the most of the non-outliers data objects to get the dataset of all possible outliers. Then，the local outlier factors are calculated on the possible outliers dataset for each data object to find out the real outliers.The experiments demonstrate that the proposed algorithm can realize the effective local outlier detection and reduce the time complexity of the algorithm.