关于Sierpinski垫片的Hausdorff测度的上方估算法实现研究
2015-09-26郭美美
郭美美
(韩山师范学院陶瓷职业技术学校,潮州 521031)
关于Sierpinski垫片的Hausdorff测度的上方估算法实现研究
郭美美
(韩山师范学院陶瓷职业技术学校,潮州521031)
0 引言
分形集的Hausdorff测度是非线性科学的一个理论课题。其中,对于具有严格自相似性的经典分形集,如关于Sierpinski垫片等,至今的结果还不多,研究发展较慢。近年来,一部分学者对于Sierpinski垫片的Hausdorff测度的研究使该课题得到了更一步的有意义的结果[1-3]。2000年在文献[3]中,提出定理1:
即通项xn满足:
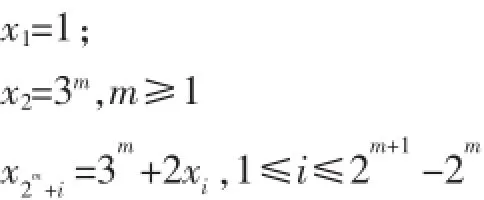
则Sierpinski垫片的Hausdorff测度有以下估值:,其中k,j为正整数且k≥2,1≤ j≤2k-2
并有一编程代码实现。
本文主要对文献[3]中的程序代码进行测试验证,并作修正,最后作进一步的延展,打破文献[3]的计算局限,得到较好的上方估算。
1 问题的提出
在文献[3]中定理1的的算法实现分为五个函数模块,各模块的作用及调用关系如图1(具体代码见文献[3]):
之所以对该算法的实现研究,是因为算法实现的运行过程中,限制了对于k值,要求不超过22。根据定理1算法的研究表明:k值越大,上方估算值越是精确。文献[3]限制k不超过22是由当时的实现算法的运行平台所局限,那么,计算机飞速发展的今天,这个局限能否得到突破,怎么突破成为关键的问题。本文把文献[3]算法的实现作延展,对于得到更精确的上估算值具有重要的意义。
2 运行环境和语法错误纠正
2.1运行环境
本文程序运行环境为处理器:Intel Core i5 CPU;内存:4GB;操作系统:64位Windows 7,C++Builder 2010。
2.2纠正几处语法错误
文献[3]运行结果如图2:
(1)关系表达式
文献[3]中:
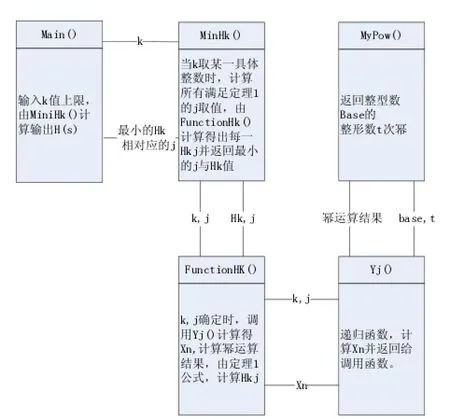
图1
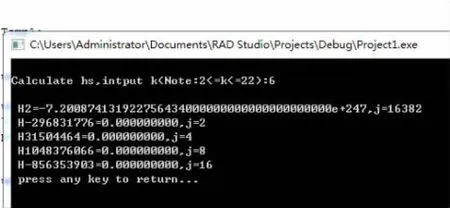
图2

其中下划线部分是用关系表达式来表达判断,必须改成j==1。

主函数main中下划线部分除了不应该用相等符号外,逻辑关系错误。从算法的理论和实现的设计来看,每次循环时,比较k=i时,Hi与TempHK1比较大小,并把两者中较小的记录于变量TempHK1。所以应该改成“>”。
(2)输出格式控制

下划线部分是long double类型的数据输出L必须为大写才能正常显示正确的数据。
(3)其他
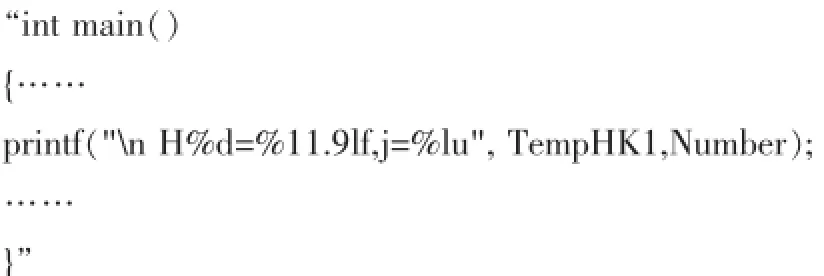
下划线部分有三个输出格式控制,输出表列却只有两个变量名。其实这里的错误,会导致在运行中途直接闪退,无法得到图1内容。只有在TempHK1前加上“i,”才可以有图2显示。
经过以上的修正后,程序的运行结果为图3:
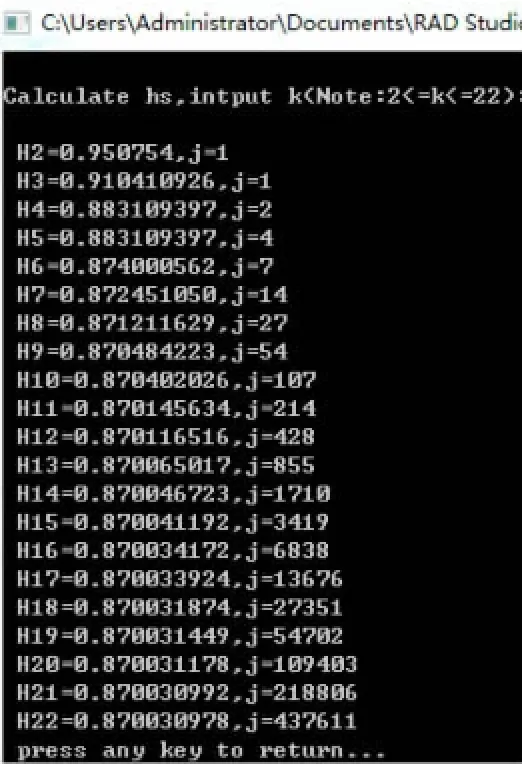
图3
3 提高计算上限
文献[3]中Hk中的k值是约束在2≤k≤22的整数。最终结果是Hk,k=22时,H(s)是最小值。然而,从算法所得规律来看,k值越大,得到的上估值就越精确。那么,如果提高k值上限或不限制是什么结果?
(1)这里先测试上限提高到30,尝试k=26结果如图4。
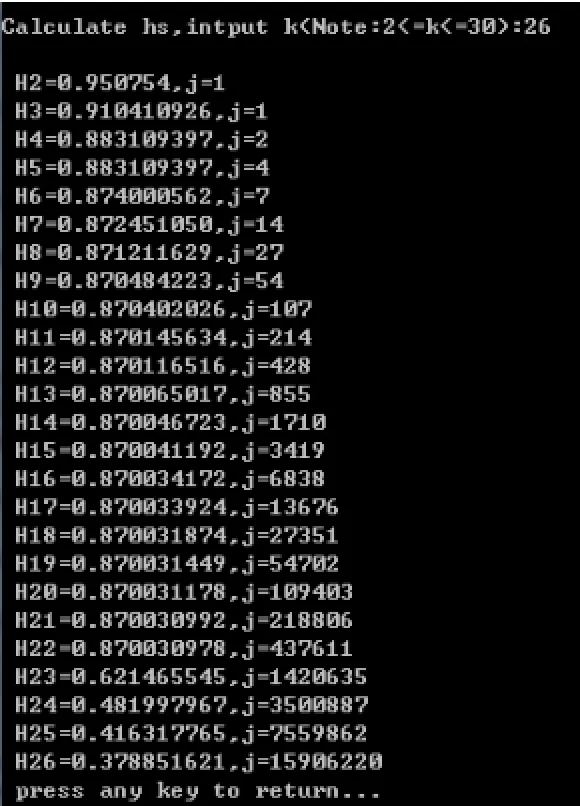
图4
由计算结果观察得知:当k=23以及其后的H值都下降得较前面快。
(2)测试k=23时,j为何值时,Hk开始急速下降。在MinHK()中增加以下代码作测试:
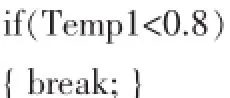
并且适当修改了主函数,只计算K=23时的所有Hk。于是测试结果如下图5:

图5
可知,当j=1048577时,是个Hk,k=23的急降点。
(3)测试Hk,k=23,j分别为1048576和1048577时各个计算过程的值。

程序运行如图6:
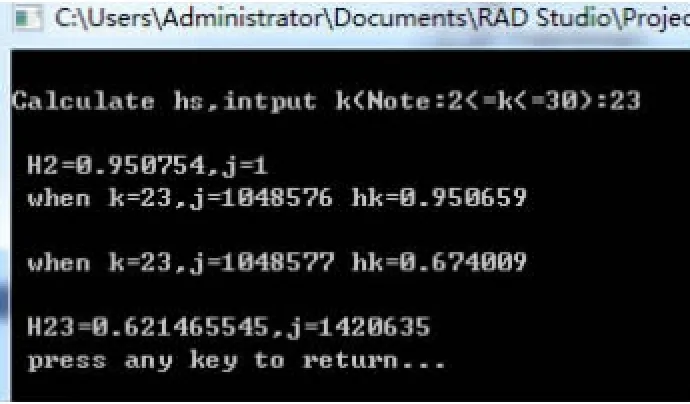
图6
这里的Hk肯定了上一步的推断,明显异常地急降。
根据文献[3]中的定理1,计算各参数在计算过程中的变化,首先验证Xn的值是否计算有误。
(4)检验Xn
当k=23,j分别为1048576和1048577时调用的计算Xn的值的函数是Yj()函数,其中,Yj调用了MyPow()函数。现在函数FunctionHK()中添加了以下下划线部分的代码,以作测试Xn:

结果如图7:
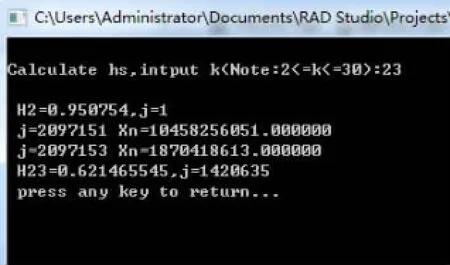
图7
根据定理1,Xn是一个不断增大的函数值,j越高,Xn越大,从图6观察说明Xn=1870418613是错误的值。对于k=23,当j=1048576×2-1时Xn是与运行程序结果一致的;当j=1048577×2-1时10460353205这个值与图7中的Xn的值是不一致的。
(5)计算321
按定理1计算Xn,涉及到一个求幂的运算。文献[3]中计算时,是调用MyPow函数的。MyPow函数的返回值是unsigned long int,这个数据类型的长度为4个字节。而321=10460353203(10)=10 0110 1111 0111 1100 0101 0010 1011 0011(2)这个数的长度超过了32bit,因此,对于函数MyPow()的调用返回值其他是丢失了最高位的数据,变成0 0110 1111 0111 1100 0101 0010 1011 0011(2)=1870418611(10),而由于丢失了最高位数据后,成为 1870418611+2= 1870418613刚好与图6的计算显示结果一致。由此得出,是计算过程中调用MyPow()函数,由于溢出导致计算结果错误。
综上所述,修改MyPow()的数据类型,就可以提高计算的上限。
4 提高上估值计算上限代码与结果
(1)修改后的代码如下:



(2)运算结果
对于输出的结果Hn表示当k=n时,j取值为m时Hs(s)的最好上估值。运算结果如图8:
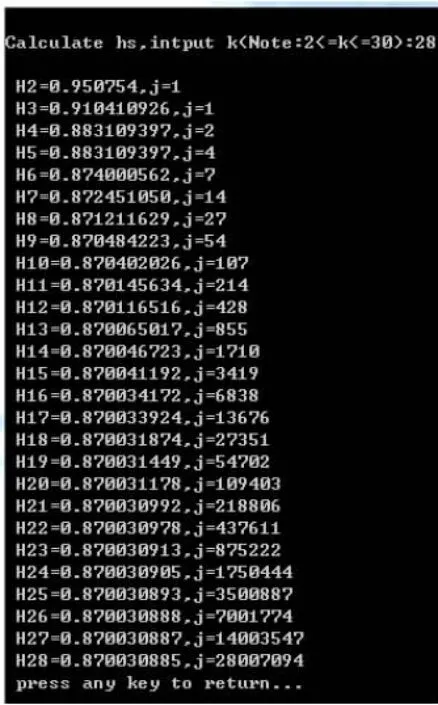
图8
5 结语
算法的实现符合定理1,保持了原算法实现的结构,并修改了文献[3]中的计算上限值,理论上可以达到66,但本文测试已花了接近一小时的计算才得图8结果,而且,对于Hn的计算结果之间的变化已不是很明显,故没再进一步作运算。但本文的算法实现已对文献[3]的算法实现作了延展,计算结果改进了文献[3]中的有关结论。
[1]Marion J.Mesures de Hausdorff D'Ensembles Fractals[J].Ann Sc Math Quebec,1981,11(1):111~137
[2]周作领.自相似集的Hausdorff测度——Kock曲线[J].中国科学(A),1998,28(2):103~107
[3]曾山,许绍元.关于Sierpinski垫片的Hausdorff测度的上估的算法.韩山师范学院学报,2000,6(2):27~31
Sierpinski Gasket;Hausdorff Measure;Algorithm Implementation
Research on the Implementation of an Algorithm for the Upper Extimation of the Hausdorff Measure of Sierpinski Gasket
GUO Mei-mei
(Ceramic Vocation Technical School,Hanshan Normal University,Chaozhou 521031)
1007-1423(2015)17-0075-06
10.3969/j.issn.1007-1423.2015.17.017
郭美美(1982-),女,广东潮州人,硕士,讲师,研究方向为软件工程
2015-04-28
2015-05-20
Sierpinski垫片的Hausdorff测度的估计和计算在分形理论上具有重要的意义。利用Sierpinski垫片的Hausdorff测度上方估算的算法,对少数的已有的计算机编程实现进行研究分析,修正文献[3]算法实现中的代码错误,并对其作进一步的延展。
Sierpinski垫片;Hausdorff测度;算法实现
国家大学生创新创业训练项目
Extimation and Calculation of Hausdorff Measure of Sierpinski Gasket has important significance.With an Algorithm for the upper extimation of the Hausdorff Measure of Sierpinski Gasket,researches and analyzes the existing implementation of an algorithm of computer,corrects paper[3]and extends to higher upper limit.
