理发师问题的Petri网模型
2015-09-26刘萍
刘萍
(甘肃民族师范学院计算机科学系,合作 747000)
理发师问题的Petri网模型
刘萍
(甘肃民族师范学院计算机科学系,合作747000)
0 引言
1962年,C.A.Petri在他的博士论文“用自动机通讯”中,首次提出Petri网的基本概念和Petri网的基本理论。Petri网是一个6元组(S,T;F,K,W,M0),其中(S,T;F)称为Petri网的基础网;基础网是有限的有向图,结点分为条件的集合S和事件的集合T。条件在图上用圆圈表示;事件在图上用矩形表示。有向图的弧只有条件指向事件的弧和事件指向条件的弧两类,弧在图上用箭头表示,F是弧的集合。K是定义在S上的容量函数,取值是非负整数。W是定义在F上的权值函数,取值是非负整数。Petri网的标识M是定义在S上的非负整数函数,M0称为Petri网的初始标识。
Petri网是研究分布式系统的建模和分析的有力的工具,这是因为Petri网特别便于描述系统中进程或部件之间的顺序、并发、冲突以及同步等关系。经过50多年的研究,Petri网已经成为具有广泛的实际应用的重要学科。
在实际应用中,Petri网对于一个问题的研究,首先需要对问题设计出一个常规的系统,然后设计这个系统的Petri网模型。进一步利用Petri网的理论对这个系统的Petri网模型进行分析。在分析中发现的任何问题都指明设计中存在的缺陷。分析这些缺陷,就可以为设计的改进提供依据。再对改进后的设计修改Petri网的模型,如此循环反复,直到分析不出有什么问题为止。
1 进程间通信(IPC)问题
进程间通信(IPC)问题是在操作系统中的重要问题。 IPC问题是作为解决在运行中的几个进程的互斥问题提出的,问题的核心是找到某种途径来防止几个进程同时读写共享的数据或文件。睡眠的理发师问题和哲学家进餐问题 (Dijkstra,1965),读者-写者问题(Courtois,1971),生产者-消费者问题,是在操作系统中关于进程间通信(IPC)问题的几个较为著名问题[2]。对于上述问题中的哲学家进餐问题,读者-写者问题,生产者-消费者问题等都有了Petri网的模型。从这些问题的Petri网的模型中,可以看到,Petri网不仅能够刻画系统的结构,而且能够描述系统的动态行为。这是利用Petri网解决实际问题的优点。在已有的文献中,我们没有看到关于睡眠的理发师问题的Petri网的模型。本文试图建立该问题的Petri模型,并且对于这种模型作出一些分析。
从Petri网的观点来看待一个系统,首先分析系统中所表现的两个基本概念:事件和条件。事件是系统中所发生的动作;系统的每一个动作都是由系统的状态所控制,而系统的状态则由一组条件来描述。因此,每一个事件的发生,总是以一些条件作为前提,这些条件称为事件的前提条件。当事件发生以后,一些前提条件消失,另外的一些条件成立,称为事件的后继条件。设t是一个事件,·t表示t的所有前提条件的集合,即·t={s| s∈S∧(s,t)∈F},称为t的前集;以t·表示t的所有后继条件的集合,即t·={s|s∈S∧(s,t)∈F}。对于一个系统,重要的工作是确定每一个事件t的前集和后集。
在Petri网中标识是很重要的概念。标识M在一定的条件下可以由事件t发动,产生新的标识,记作M[t>。从M0经过发动能够产生的所有标识的集合记为R(M0)。R(M0)可以按照发动的次序列成树称为Petri网的可达标识树。
2 理发师问题
理发店中有三名理发师A,B,C,每人一張理发椅子,等待室有5张供顾客等待的休息椅子。如果有空闲的休息椅子,顾客进入理发店就可以坐下等待。理发过程分为两个工序:工序1是A为顾客服务,工序1完成以后,顾客分男,女由B或C提供第2道工序的服务。B或C服务完成以后,由收银员收取理发费,顾客离开理发店。

顾客的行为:顾客进入理发店看到有空闲的休息椅子,就坐下等待。如果没有空闲的休息椅子,顾客就离开理发店。等待休息的顾客看到A的理发椅子空出,先到的顾客就坐上,并且唤醒理发师A为自己理发(工序1)。工序1完成后,如果B或C仍然为上一个顾客服务,则这个顾客仍然坐在A的椅子上等待,否则顾客坐上B或C的理发椅子,并且唤醒B或C为自己理发(工序2)。工序2完成后,顾客唤醒收银员,交付理发费,离开理发店。
理发师,收银员行为:理发师为顾客完成了一道理发工序以后休息(睡觉);等待被下一个顾客唤醒,为下一个顾客服务。收银员收取顾客的理发费以后休息(睡觉),等待被下一个顾客唤醒,收取理发费。理发师的行为和收银员行为是循环的(从理发店开门到关门)。
理发店的状态由顾客和理发员、收银员的行为决定。

在理发师问题中,顾客的行为和理发师(收银员)的行为是Petri网的所有的事件。下面讨论顾客的行为的事件和理发师的行为的事件。
a1-有一名顾客进入理发店;
a2-顾客在休息椅子上坐下;
a3-顾客叫醒理发师A开始理发的第1道工序;
a4-A完成为顾客理发的第1道工序;
a5-顾客叫醒理发师B开始理发的第2道工序;
a6-B完成为顾客理发的第2道工序;
a7-顾客理发完毕唤醒收银员,付钱离开理发店;
a8-顾客叫醒理发师C开始理发的第2道工序;
a9-C完成为顾客理发的第2道工序;
a10-顾客理发完毕唤醒收银员,付钱离开理发店。

下面分析理发店的各种状态,即Petri网的所有的条件。
S1-理发师A休息(睡觉);
S2-理发师B休息(睡觉);
S3-理发师C休息(睡觉);
S4-收银员休息(睡觉);
S5-休息室有顾客(最多容纳5人,设置S5的容量K=5来控制);
S6-顾客坐在A的理发椅子上;
S7-顾客接受理发师A第1道工序的服务;
S8-理发师A第1道工序的服务完成,顾客等待第2道理发工序;
S9-顾客接受理发师B第2道工序的服务;
S10-理发师B完成理发的第2道工序;
S11-顾客接受理发师C第2道工序的服务;
S12-理发师C完成理发的第2道工序。

下面计算在2.1中出现的事件的前提条件和后继条件。

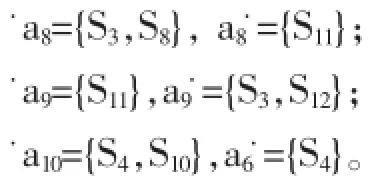
3 理发师问题的Petri网
下面根据2.5的计算给出理发师问题的Petri网。规定每一条弧的权值为1;S5的容量为5,其余各条件的容量都是1,如图1所示。
4 理发师问题的Petri网的可达标识树
为了使得理发师问题的Petri网能够运行,需要给出初始标识。由于S5的前提事件所以S5可以通过a1的发动获得标识,不需要预先设置标识。S1,S2,S3和S4在运行中是循环出现的条件,因此必须预先设置标识。因此M0={S1,S2,S3,S4}。R(M0)包括以下9个标识:
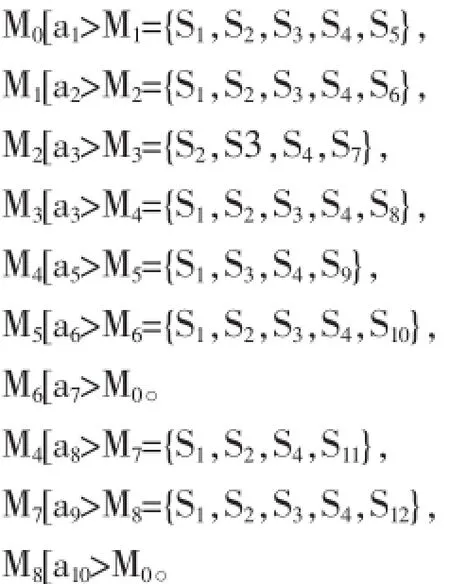
可达标识树如下:

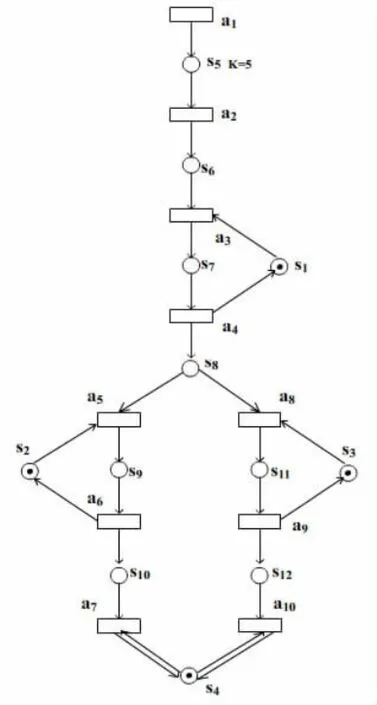
图1
[1]Petri C.A..Kommunikation Mit Automaten,Bonn,1962
[2]Peterson J.L..Petri网理论与系统模拟.吴哲辉译.中国矿业大学出版社,1989
[3]吴哲辉.Petri网导论.北京:机械工业出版社,2006
[4]袁崇义.Petri网原理.北京:电子工业出版社,1998
[5]袁崇义.Petri网原理与应用.北京:电子工业出版社,2005
[6]刘萍.关于Petri网的代数结构.甘肃高师学报,2014(2)
[7]刘萍.出现网的抽象描述.甘肃高师学报,2014(5)
[8]刘萍.出现网的S切.现代计算机,2014(7)
Petri Net;Problem of Barbers;Reachability Tree of Markings
Petri Net Model on the Problem of Barbers
LIU Ping
(Department of Computer Science,Gansu Normal University for Nationalities,Gansu 747000)
1007-1423(2015)17-0059-04
10.3969/j.issn.1007-1423.2015.17.013
2015-04-29
2015-06-10
讨论在操作系统中研究的关于进程间通信(IPC)的一个著名的问题:睡眠的理发师问题。给出这个问题的Petri网模型和这个Petri网的可达标识图性质。
Petri网;理发师问题;可达标识图
甘肃民族师范学院院长基金(No.2013-16)
刘萍(1978-),青海西宁人,硕士,讲师,研究方向为Petri网、数据库理论
Discusses the Petri net model on the problem of barbers.The problem of Barbers is an important problem in operating systems.Carries out the Petri net model of the problem,and the property of the reachability tree of markings.
