基于齿距偏差曲面的面齿轮齿距偏差测量
2015-09-24唐进元李武俊张燕王艺欣雨
唐进元,李武俊,张燕,王艺欣雨
基于齿距偏差曲面的面齿轮齿距偏差测量
唐进元,李武俊,张燕,王艺欣雨
(中南大学 机电工程学院,高性能复杂制造国家重点实验室,湖南 长沙,410083)
基于面齿轮传动的特点,为获得准确可靠的面齿轮的齿距偏差,参考其他类型齿轮齿距偏差定义,提出相邻齿面的面齿轮齿距偏差曲面及齿距法向偏差曲面概念,构建基于三坐标测量机获得面齿轮齿距偏差曲面及齿距法向偏差曲面方法:通过三坐标测量机得到实际面齿轮齿面数据,构建其真实数值齿面,选定基准齿面,将相邻真实齿面旋转理论夹角得到齿距偏差曲面。给出对面齿轮齿距偏差曲面进行分析获取齿距偏差数据的方法与步骤。研究结果表明:面齿轮齿距偏差曲面、齿距法向偏差曲面概念及测量方法、齿距偏差数据获取方法的提出为面齿轮制造误差评价提供一种新方法。
三坐标测量仪;面齿轮;齿距偏差曲面;齿距法向偏差曲面;齿距偏差
面齿轮传动是一种新型齿轮传动,国外已经设计制造出采用面齿轮传动的军用直升机主减速器,其在体积小、质量轻、高承载能力、低噪声、高可靠性、长寿命及良好的功率分流效果等方面显示了极大的优势[1−3]。国内也越来越重视面齿轮设计及加工技术的研究,中南大学、北京工业大学、南京航空航天大学、北京航空航天大学等单位已成功试制出面齿轮。但是,评定加工后的齿轮精度,验证齿轮型面是否符合设计要求,目前还有很多问题需要解决。齿面精度测量方法有齿轮啮合测量仪(GMI)方法和三坐标测量仪(CMM)方法2类[4]。CMM方法在现代齿轮制造行业的应用越来越广泛。相对于其他齿轮专用测量仪器,三坐标测量机不仅可以通过开发不同的软件模块测量各种齿轮齿面各点的坐标误差,而且还可以通过分析得到各种误差信息。齿面误差包括趋势误差、周期误差和面噪声[5]。通常由加工过程中诸如机床、刀具、操作等不同的工艺因素所致。齿形方面的趋势误差主要是由刀具(或砂轮)误差所致, 齿向误差主要是由齿轮加工时齿轮轴线或刀架导轨倾斜所引起的。对于弧齿锥齿轮,很多学者[6−8]对CMM数据提取处理、误差分析及评定进行了深入的研究。Goch[4]综述了圆柱齿轮(直齿轮、斜齿轮)、螺旋锥齿轮的精度测量研究中的测量方法及各种方法的优缺点,并指出三坐标测量方法的优越性。Pfeifer等[9]利用三坐标测量机测量螺旋锥齿轮的齿面三维坐标数据,利用他们开发的算法补偿测头导致的误差,并分析了含齿形修形、鼓形修形和制造误差的0阶、1阶、2阶偏差。张军辉等[10]利用三坐标测量机测得弧齿锥齿轮齿面上离散点坐标,利用双三次NURBS曲面拟合,得到数字化齿面。李天兴等[11]通过测量齿面误差来修正机床运动参数。由于面齿轮设计、加工及在工业中的应用相对其他齿轮传动而言,仍处于小规模应用阶段,此类零件的误差测量及误差等级评定尚未形成标准,还没有相应的用于齿轮测量机(中心)及三坐标测量机的测量软件。王志等[12]分析了由于测量坐标系和面齿轮设计坐标系不重合及测头球心和接触点不重合引起的误差,并给出了误差补偿公式。王延忠等[3, 5]利用齿轮测量中心得到实际测量数据,并与理论数据进行比较, 获得齿形偏差曲面。圆齿轮齿距偏差在是指节圆圆周上实际测量齿面点与理论齿面点的误差,圆柱齿轮是线接触,用节圆圆周上点的齿距偏差来评价齿轮精度是合理的。但是面齿轮为点接触传动,接触区域集中在齿面的一个局部区域,在齿轮的不同径向位置理论齿距是不相等的,所以需要用一个齿距偏差曲面来表征齿轮的齿距偏差。针对面齿轮齿面结构的特征,定义面齿轮齿距、获得面齿轮齿距偏差数值是面齿轮测量研究急待解决的问题。本文作者基于三坐标测量机测量数据得到面齿轮齿面三维数据,重构实际数值齿面,研究齿面齿距偏差面测量和数据处理方法、齿距偏差信息提取方法,以期对面齿轮齿距测量研究提供新的方法。
1 面齿轮坐标测量关键技术
1.1 测量仪器及测量齿轮
采用海克斯康GLOBAL STATUS-5.7.5型三坐标测量机,行程范围(××)为500 mm×700 mm×500 mm,长×宽×高为1 025 mm×1 480 mm×2 431 mm,如图1所示,待测量的齿轮如图2所示。

图2 面齿轮实物图
三维坐标测量仪的最小测量值为1 μm,累积测量精度为1 μm,测量球头的半径为2 mm。测量软件中,含有测量球头半径的补偿功能,为了避免由测头半径导致的偏差[12],本文的测量结果均为补偿后的真实齿面的三维坐标数据。
对于触发测头而言,每个点的检测都要经过“启 动—触发—回退—停止”的过程,测头的路径由3段组成:测头接触被测表面存取坐标值后回退的距离;从回退位置到下一个定位点的距离;测头接触工件表面的检测距离。
由于测量点为面齿轮各齿的同侧齿面点,测量时测头的运动轨迹为两点间的最短距离即沿着直线在各测点间运动,因此需要在各理论点之间加入安全点,以防测头与零件发生碰撞。选取理论测点正上方的某一点作为测量的安全点,这样测头的运动路径就是先移动至安全点,由安全点快速移动到逼近点,由逼近点沿着测点法矢方向逼近直至接触到零件,与零件接触的点即为实测点,然后再由实测点沿着法矢方向回退一个回退距离,再运动到下一个安全点。
1.2 测量区域与测量坐标系选取
对于直齿轮,单个齿距偏差的计算可以在极坐标下对齿轮的分度圆依次采点测量,所采的点为同侧齿面与分度圆的交点,高度定为齿宽的一半[13]。对于面齿轮目前没有统一的标准,而且齿面点的法向矢量从外端到内端逐渐增大[14],外端附近近似为一平面。但是面齿轮与配对的直齿轮接触时,接触轨迹靠近内端,如图3所示,图3是通过自主开发的面齿轮TCA软件分析得到,接触分析的面齿轮传动参数见表1,其中的面齿轮如图2所示。

图3 面齿轮接触轨迹

表1 面齿轮传动参数
接触轨迹确定之后,测量区域的位置应由接触轨迹确定,即测量区域应该最大限度包含接触轨迹。测量坐标系与三维模型坐标系相同,以面齿轮的上端面作为基准平面,以面齿轮外圆圆心作为坐标系和方向的中心,以齿槽中线作为旋转轴的负向,将轴中心平移到基准平面上,如图4所示。图4中-为测量坐标系,P为待测点,为测点到旋转轴的距离,即,,Z为测点的高度。
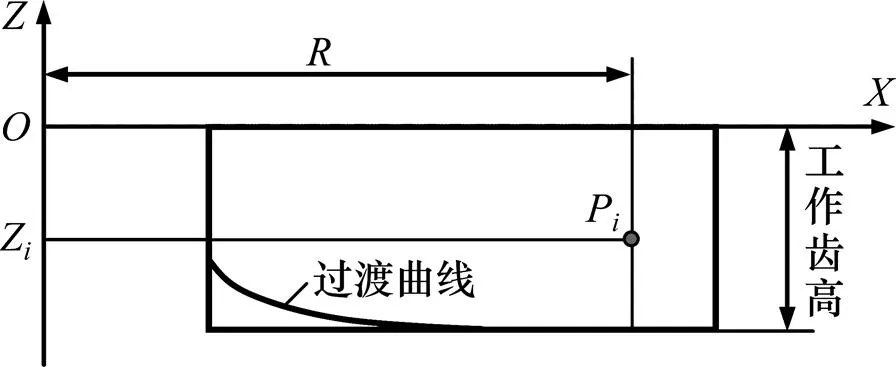
图4 测量区域与坐标系示意图
2 面齿轮齿距偏差曲面及齿距法向偏差曲面
2.1 面齿轮齿距偏差曲面及齿距法向偏差曲面定义
根据GB/T 10095.1—2008,圆柱齿轮单个齿距偏差定义为:在端平面上,在接近齿高中部一个与齿轮轴线同心的圆上,实际齿距与理论齿距的代数差。该定义假设圆柱齿轮在齿宽方向偏差分布一致,主要是针对齿轮精度评价标准提出,啮合过程为理想的线接触过程。但是对于面齿轮这类空间曲面齿轮,采用单点齿距偏差衡量齿轮的精度将带来偏差。因为:1) 面齿轮的啮合过程为点接触,从端面的外端到内端,理论齿距不是常值,用单点得到的齿距偏差不能精确作为齿轮综合精度的评价标准。2) 以实际相邻齿面为基准的齿距偏差曲面能全面反映整个齿面范围的齿距偏差。3) 从齿轮动力学传递误差激励的角度,真实相邻齿面的齿距偏差可以直接转化为齿轮的静态传递偏差激励。4) 相邻齿面齿距法向偏差曲面即为轮齿接触的静态间隙。静态传递偏差和间隙是齿轮动态性能分析的重要参数,通过测量分析可以为面齿轮动力学研究提供基础数据。
综上,在面齿轮测量中,面齿轮齿距偏差不能完全借用圆柱齿轮单个齿距偏差定义,而应该从整体的角度考量,因此提出面齿轮齿距偏差曲面及齿距法向偏差曲面的概念。
则通过得到旋转后的齿面坐标值′及对应的法向量为

由于对面齿轮的齿距偏差还没有相关标准规定,参考螺旋锥齿轮及直齿轮的相关规定,定义面齿轮的齿距偏差为:相同的高度(Z)时,平行于平面的圆曲线与齿面的同向齿槽交点的弧长为齿距,实际齿距与理论齿距的差值即为面齿轮单个齿距偏差。根据面齿轮的啮合特征,采用三坐标测量时,将给出选择测量区域内的齿距偏差曲面。
将测量齿面转换为极坐标形式
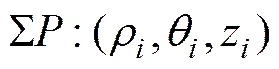
旋转后的齿面为
齿距偏差为
另外,定义面齿轮齿距法向偏差为
式中:P为第个齿面上一点;P+1为相邻第+1个齿面上与P位置相同的点;为P+1旋转角度后的点;n为P的法向量。齿距法向偏差曲面为一系列测量点的齿距法向偏差形成的曲面。
2.2 基于面齿轮齿距偏差曲面的齿距偏差获取方法
2.2.1 齿距法向偏差曲面及等高线图
将CMM测量得到的数据保存为TXT文档,并将其读入Matlab中,得到4个实际测量曲面,如图5所示。图5(a)所示为2个相邻齿面(齿对1),图5(b)所示为位置相差90°的两相邻齿面(齿对2),2组相邻齿面均以黑色齿面为基准。经过坐标旋转后,与另一相邻测量齿面测量点之间的距离形成的曲面即为偏差曲面。齿距法向偏差曲面及等高线图如图6所示。从图6可以看出:在测量区域内,最大的齿距法向偏差为33.4 μm,最小的齿距法向偏差为−45.1 μm,但是在接触区域内,在产生轮齿接触的区域内齿距法向偏差为±20 μm。

(a) 齿对1;(b) 齿对2

(a) 偏差曲面;(b) 等高线图
2.2.2 基于齿距偏差曲面及等高线图的齿距偏差获取
图7和图8所示分别为齿对1和齿对2的齿距偏差曲面及等高线图。从图7和图8可以看出:最大的齿距偏差出现在内齿端及外齿端的齿顶附近,其偏差值远大于齿面内部的齿距偏差值。相应地在等高线图中在接触区域内,齿对1的齿距偏差为±10 μm (图中数值为0.01),齿对2的齿距偏差为±20 μm (图中数值为0.02)。

(a) 偏差曲面;(b) 等高线图

(a) 偏差曲面;(b) 等高线图
3 结论
1) 提出了面齿轮齿距偏差曲面及齿距法向偏差曲面概念。
2) 以某一真实齿面为基准,将相邻齿面旋转理论夹角,计算得到了相邻的真实齿面的齿距法向偏差曲面及面齿轮齿距偏差曲面。
3) 测量数据分析表明在接触区域附近,齿面的齿距偏差较小。
4) 得到的面齿轮齿距偏差曲面及齿距法向偏差曲面概念及测量方法、齿距偏差数据获取方法与步骤解决了面齿轮齿距偏差测量中存在的问题,为面齿轮制造误差评价提供一种新方法。
[1] 朱如鹏. 面齿轮传动的啮合特性研究[D]. 南京: 南京航空航天大学机电学院, 2000.
ZHU Rupeng. An investigation on the meshing characteristics of face gear drives[D]. Nanjing: Nanjing University of Aeronautics & Astronautics. College of Mechanical and Electrical Engineering, 2000.
[2] WANG Zhi, SHI Zhaoyao. Theory analysis of error in orthogonal face gear measurement by CMM[J]. Journal of Beijing University of Technology, 2012, 5(4): 663−667.
[3] 王延忠, 王庆颖, 吴灿辉, 等. 正交面齿轮齿面偏差的坐标测量[J]. 机械传动, 2010, 34(7): 1−4.
WANG Yanzhong, WANG Qingying, WU Canhui, et al. Deviation of face gear real tooth surface determined by coordinate measurements[J]. Journal of Mechanical Transmission, 2010, 34(7): 1−4.
[4] Goch G. Gear metrology[J]. CIRP Annals: Manufacturing Technology, 2003, 52(2): 659−695.
[5] 张俐, 丁志耀, 王延忠. 面齿轮齿面的自适应采样方法[J]. 北京航空航天大学学报, 2012, 38(2): 247−251.
ZHANG Li, DING Zhiyao, WANG Yanzhong. Adaptive sampling method of face gear tooth surface[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 247−251.
[6] 方宗德, 曹雪梅, 张金良. 航空弧齿锥齿轮齿面坐标测量的数据处理[J]. 航空学报, 2007, 28(2): 456−459.
FANG Zongde, CAO Xuemei, ZHANG Jinliang. Measuring date processing of aviation spiral bevel gears by using coordinate measurement[J]. Acta Aeronautica Et Astronautica Sinica, 2007, 28(2): 456−459.
[7] 曹雪梅, 王军, 张海英. 弧齿锥齿轮齿面误差检测与实验验证[J]. 中国机械工程, 2009, 20(15): 1799−1801.
CAO Xuemei, WANG Jun, ZHANG Haiying. Geometric error measurement of spiral bevel gears and experimental test[J]. China Mechanical Engineering, 2009, 20(15): 1799−1801.
[8] 赵华. 基于三坐标的弧齿锥齿轮齿面误差测量与评定 [J]. 机械传动, 2011, 35(5): 20−26.
ZHAO Hua. The tooth surface error measurement and evaluation of spiral bevel gear based on three-coordinate measurement[J]. Journal of Mechanical Transmission, 2011, 35(5): 20−26.
[9] Pfeifer T, Kurokawa S, Meyer S. Derivation of parameters of global form deviations for 3-dimensional surfaces in actual manufacturing processes[J]. Measurement, 2001, 29(3): 179−200.
[10] 张军辉, 方宗德, 王成. 基于 NURBS 的弧齿锥齿轮真实齿面的数字化仿真[J]. 航空动力学报, 2009, 24(7): 1−5.
ZHANG Junhui, FANG Zongde, WANG Cheng. Digital simulation of spiral bevel gears, real tooth surfaces based on non-uniform rational B-spline[J]. Journal of Aerospace Power, 2009, 24(7): 1−5.
[11] 李天兴, 邓效忠, 李聚波. 螺旋锥齿轮齿面误差分析与自动反馈修正[J]. 航空动力学报, 2011, 26(5): 1194−1200.
LI Tianxing, DENG Xiaozhong, LI Jubo. Automatic feedback correction and deviation analysis for tooth surface of spiral bevel and hypoid gear[J]. Journal of Aerospace Power, 2011, 26(5): 1194−1200.
[12] 王志, 石照耀. CMM 测量正交面齿轮的误差理论分析[J]. 北京工业大学学报, 2012, 5(4): 663−667.
WANG Zhi, SHI Zhaoyao. Theory analysis of error in orthogonal face gear measurement by CMM[J]. Journal Of Beijing University Of Technology, 2012, 5(4): 663−667.
[13] 曹爱文, 陈定溪, 张海. 三坐标测量机在齿轮齿距偏差测量中的应用[J]. 工具技术, 2009, 42(12): 99−101.
CAO Aiwen, CHEN Dingxi, ZHANG Hai. Application of CMM in measurement of gear’s teeth space deviations[J]. Tool Engineering, 2009, 42(12): 99−101.
[14] 鲁文龙, 朱如鹏. 正交面齿轮传动中齿面曲率研究[J]. 南京航空航天大学学报, 2000, 32(4): 400−404.
LU Wenlong, ZHU Rupeng. Curvature research on the tooth surface of Orthogonal face gear transmission[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2000, 32(4): 400−404.
Measuring and calculating method of face gear pitch deviation based on tooth deviation surface
TANG Jinyuan, LI Wujun, ZHANG Yan, WANG Yixinyu
(State Key Laboratory of High Performance and Complex Manufacturing,School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
To evaluate the accuracy grade of face gear and perform dynamic analysis, the pitch deviation surface and normal deviation surface relative to the real tooth surface were proposed. Firstly, the concepts and calculation method of pitch deviation surface and normal deviation surface of face gear based on the coordinate measuring machine (CMM), were discussed. According to the measured real gear face data, the real numerical gear tooth surface was reconstructed. The adjacent contacting gear surface was rotated at the theoretical anglebased on one real gear surface, and the pitch deviation gear surface was derived. Finally, an experiment was performed to illustrate and validate the proposed method, which provides the basic data for the subsequent dynamic characteristic analysis. The results show that the proposed concepts and calculation method of pitch deviation surface provide a new strategy to evaluate the manufacturing error of face gear.
CMM; face gear; pitch deviation surface; normal deviation surface; pitch deviation
TH132.41
A
1672−7207(2015)02−0459−06
2014−03−30;
2014−06−29
国家重点基础研究发展计划(973计划)项目(2011CB706800);国家自然科学基金资助项目(51275530)(Project (2011CB706800) supported by the National Basic Research Development Program (973 Program); Project (51275530) supported by the National Natural Science Foundation of China)
唐进元,教授,从事复杂曲面零件设计与制造研究;E-mail:jytangcsu@163.com
10.11817/j.issn.1672-7207.2015.02.012
(编辑 赵俊)
