高重合度与低重合度齿轮系统动力学分岔特性对比分析
2015-09-24李发家朱如鹏鲍和云叶福民靳广虎
李发家,朱如鹏,鲍和云,叶福民,靳广虎
高重合度与低重合度齿轮系统动力学分岔特性对比分析
李发家,朱如鹏,鲍和云,叶福民,靳广虎
(南京航空航天大学 机电学院,江苏省精密与微细制造技术重点实验室,江苏 南京,210016)
针对高重合度齿轮和低重合度齿轮,采用有限元方法计算其啮合刚度;建立含齿侧间隙和时变刚度的齿轮系统的扭转振动模型,对模型啮合线位移解的分岔特性和跳跃性进行研究。研究结果表明:当忽略误差,仅考虑齿侧间隙的影响时,高重合度齿轮系统啮合线位移的解,连续平稳,不存在跳跃现象,低重合度齿轮系统啮合线的位移解,多处发生了跳跃现象;齿频误差激励在高速区域(无量纲转速为1.1~2.1区域)其对低重合度齿轮的动力学影响要大于对高重合度齿轮的影响;随着偏心误差的增加,啮合线位移增加,系统的周期稳定性逐渐降低,偏心误差对普通齿轮的影响比高重合度齿轮的影响要大;在误差作用下,高重合度齿轮的周期稳定性要高于普通齿轮的周期稳定性,运行更加平稳,采用高重合度齿轮可以降低齿轮的振动和噪声。
高重合度;齿轮系统;动力学;分岔;稳定性
高重合度(HCR)齿轮传动是重合度大于等于2的齿轮传动,同时啮合的轮齿对数较多,单对轮齿承受的载荷小,具有承载能力大、传动平稳等优点,因此,高重合度的齿轮传动备受关注。许多学者对齿轮传动的动力学特性进行了大量研究。Theodossiades等[1]对考虑时变刚度和传动误差的单自由度齿轮扭转模型的跳跃性和典型庞加莱截面进行了研究;Parker等[2]建立了两自由度齿轮动力学模型,分析了齿轮在不同转动频率下的传动误差的跳跃性;Saghafi[3]建立了两自由度齿轮模型,对系统全局分岔和混沌特性进行了研究;Tamminana等[4−6]分析了考虑轴承径向支承和齿侧间隙对三自由度直齿轮系统的非线性动力学特性影响;Wang等[7−8]学者采用有限元法对高重合度齿轮的齿间载荷分布、齿根弯曲应力和接触应力进行了计算,但未对高重合度齿轮的动力学特性进行研究;刘梦 军[9]建立含间隙的单对齿轮副非线性动力学模型,对模型的动态特性进行了研究;刘晓宁等[10]研究三自由度齿轮的稳定性、分岔类型;赵宁等[11]以重合度最大、体积最小、弯曲强度相等为目标对高重合度齿轮进行了优化,其研究未涉及动力学内容;渠珍珍等[12−13]对高重合度齿轮的实现和动态特性进行了分析研究,给出了高重合度行星齿轮的动态特性,但未对高重合度齿轮的分岔跳跃等特性进行研究;张祖芳等[14]对不同重合度的齿轮副运动进行了研究,求解了不同载荷和转速下的时域图、相图和频率图,未对高重合度齿轮的分岔特性进行研究;方宗德等[15]对高重合度齿轮的载荷分配,刚度计算和动态特性进行了计算和研究,给出大重合度直齿轮副的优化设计方法,同样未对高重合度齿轮系统周期稳定性和跳跃性进行研究。在此,本文作者采用有限元的方法计算高重合度齿轮和低重合度齿轮的啮合刚度,利用傅里叶级数拟合高重合度齿轮和低重合度齿轮的啮合刚度,对高重合度齿轮和低重合度齿轮的动力学分岔特性及跳跃性进行研究。
1 系统模型简化
仅考虑扭转振动的齿轮副扭转动力学模型如图1所示。图1中:p和g分别为主动齿轮p和从动齿轮g所受的扭矩;p和g分别为两齿轮的旋转自由度;p和g分别为主动齿轮和从动齿轮的基圆半径;为齿侧间隙的一半;()为齿轮啮合的综合误差;m为齿轮副的啮合阻尼;m为齿轮副之间的啮合刚度。
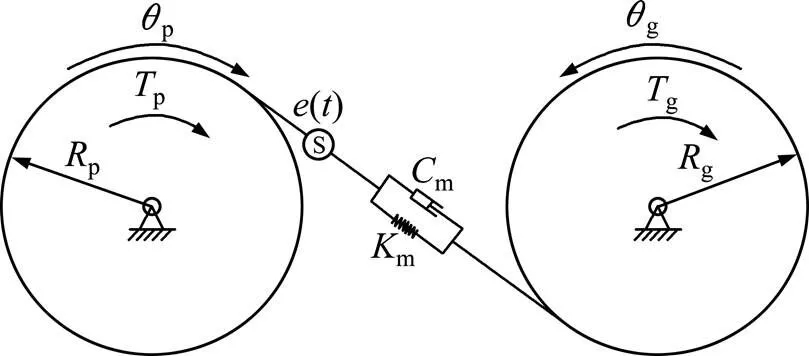
图1 齿轮副扭转模型
图1所示的齿轮副的扭转振动方程为
式中:p和g分别为主动齿轮和从动齿轮的转动惯量;(,)为齿轮副啮合线间位移函数。
1.1 齿轮啮合时变刚度计算和拟合
齿轮重合度是表示同时啮合的轮齿对数的参数,可通过改变齿轮的基本参数,改变齿轮的重合度。本文采用改变齿顶高系数方式增加齿轮的重合度,所采用的齿轮参数和重合度系数如表1所示。
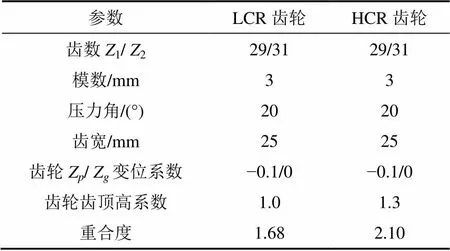
表1 齿轮传动系统传动齿轮基本参数
建立表1参数的齿轮有限元模型,对其刚度进行计算,得到齿轮啮合刚度如图2所示,HCR齿轮和LCR齿轮的平均刚度分别为3.85×108N/m和3.75×108N/m。采用六阶Fourier级数拟合齿轮啮合刚度得到齿轮啮合刚度拟合曲线如图2所示,拟合方程的各次谐波参数如表2所示。
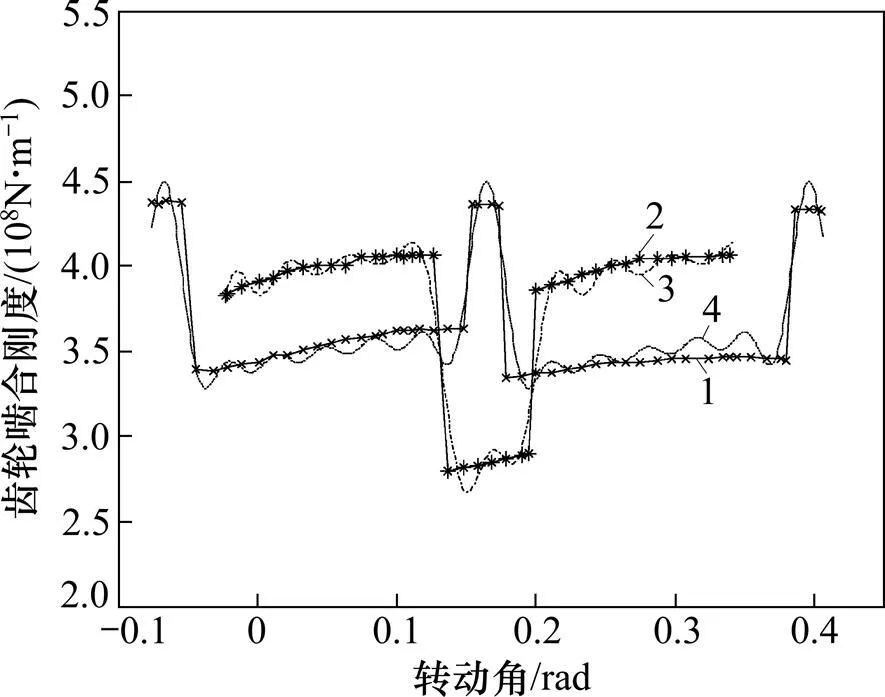
1—HCR齿轮计算计算刚度;2—LCR齿轮计算刚度;3—HCR傅里叶拟合刚度;4—LCR齿轮傅里叶拟合刚度
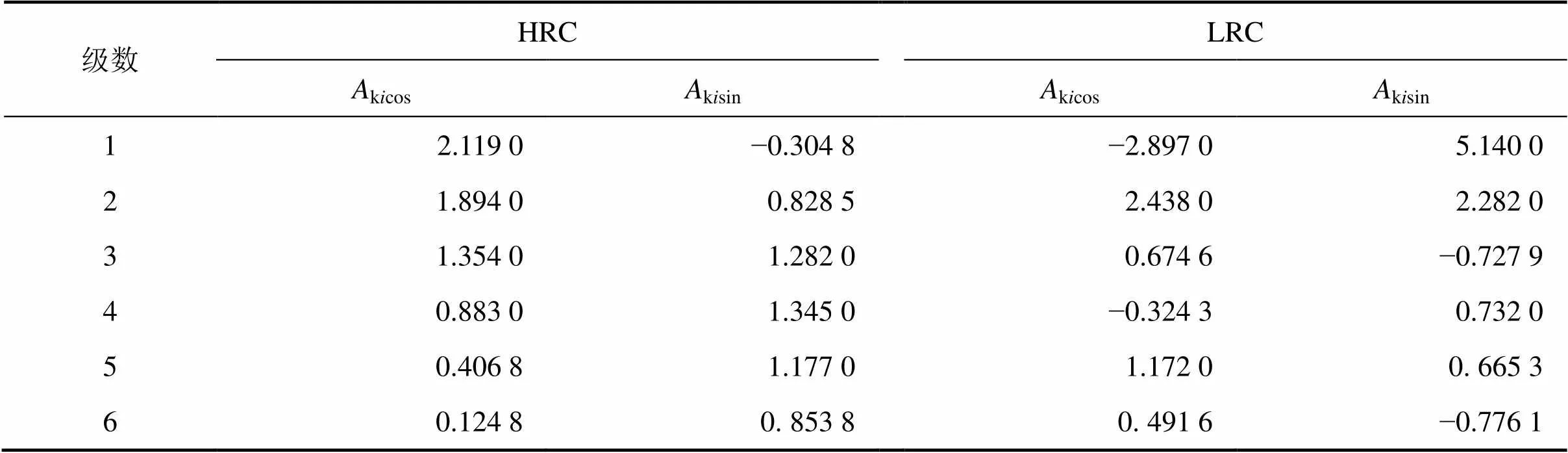
表2 刚度的各次谐波参数
注:kisin为傅里叶拟合方程中各阶正弦项的系数;kicos为傅里叶拟合方程中各阶余弦项的系数。
齿轮副间的啮合力由构件在啮合线上的等效位移和啮合刚度确定,模型的啮合线上等效位移由2部分位移沿啮合线投影组成,即齿轮各种误差在啮合线上的投影和齿轮转动位移在啮合线上的投影。
由误差引起的在啮合线上的位移投影为
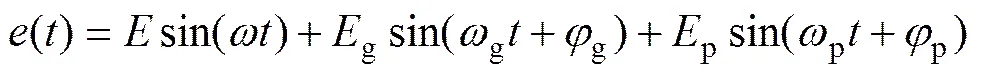
式中:为齿频误差;g和P分别为齿轮g和齿轮p的安装误差;g和p分别为齿轮g和齿轮p初相位;g和p分别为齿轮g和齿轮p的转动角速度。
定义啮合线的等效位移为
齿轮系统中不可避免地存在齿侧间隙,间隙为非线性齿轮系统的强非线性因素,齿轮系统啮合线等效位移的间隙函数为
1.2 方程的无量纲化
引入式(3)将式(1)简化为
2 齿轮转速对无误差齿轮系统分岔和稳定解跳跃特性的影响
采用4阶Runge-Kutta求解无量纲式(6),齿轮参数如表2所示。对系统的动力学特性进行研究,输入功率200 kW,齿侧间隙初始值取为50 μm,位移标称尺度为10 μm。
由于重合度对刚度的影响较为显著,现忽略其他因素及式(2)中()对系统的影响,即:=0,E=0,p=0,仅考虑由于重合度的刚度变化造成的内部激励对齿轮系统的分岔和跳跃特性的影响。
2.1 转速对分岔特性的影响
齿轮系统的啮合阻尼比取0.035时,系统的啮合线位移,HCR齿轮随无量纲转速变化的分岔特性如图3所示,LCR齿轮的分岔特性如图4所示。
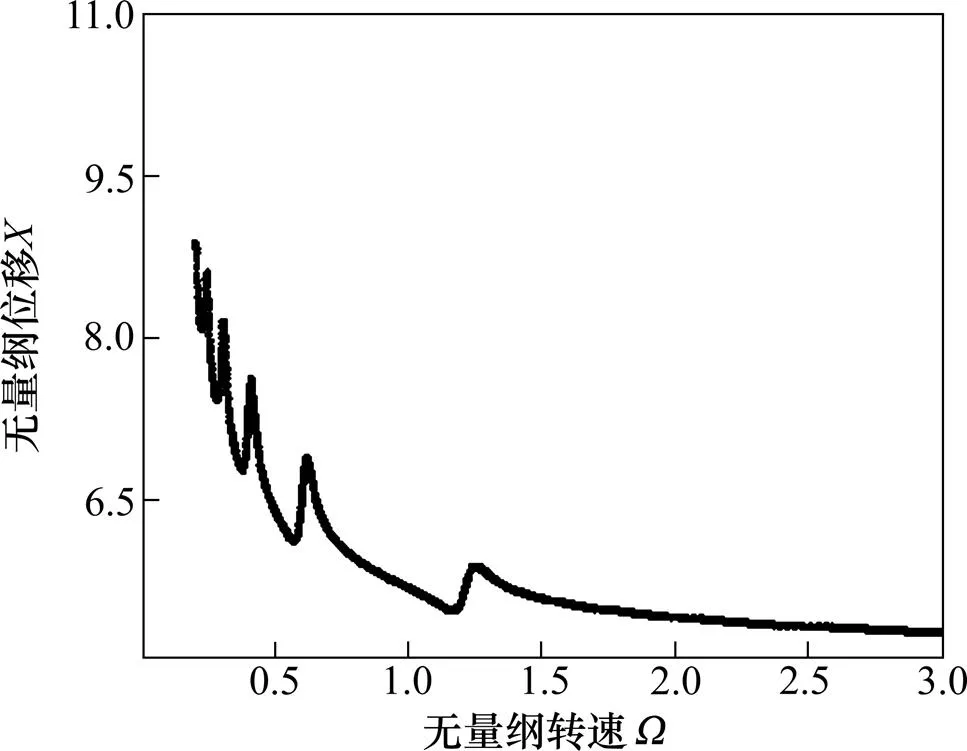
图3 HCR齿轮啮合线位移随转速全局分岔
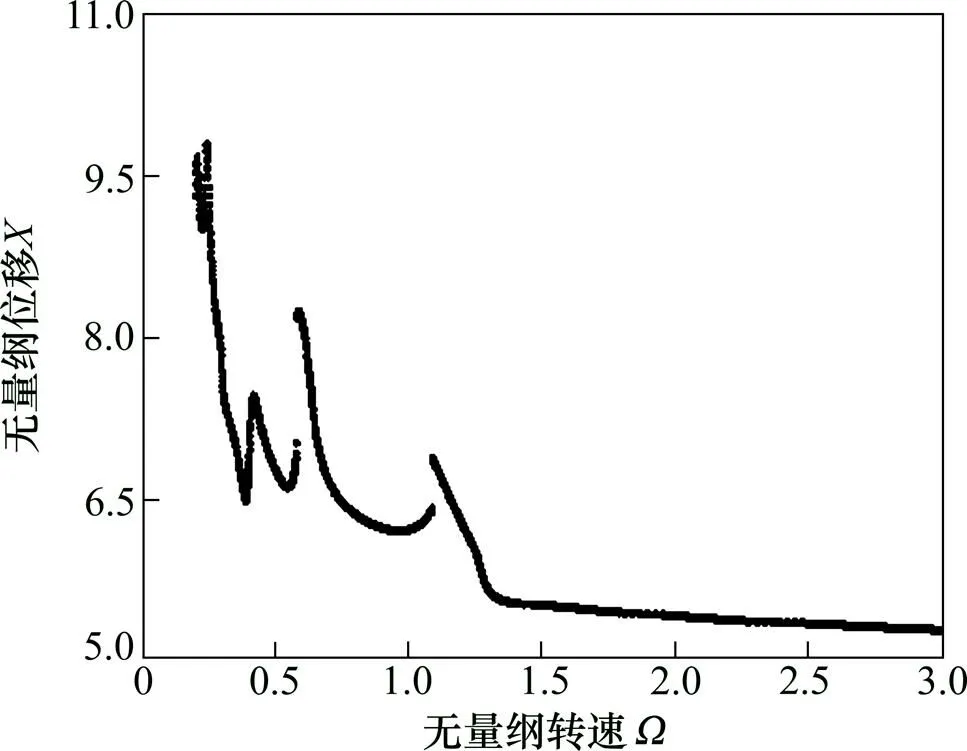
图4 LCR齿轮啮合线位移随转速全局分岔
由图3和图4可知:在仅考虑扭转的齿轮系统中刚度对系统的分岔特性影响较小,系统未发生明显的分岔现象;但LCR齿轮的啮合线的位移发生跳跃现象,同时存在2处明显的跳跃点,HCR齿轮啮合线的位移未发生跳跃现象,系统的运行连续。由于跳跃和系统运行的周期稳定相关,因此,需要对该情况下的运行多值性和跳跃现象进行研究。
2.2 转速对稳定解跳跃特性的影响
系统在不同的初值条件下可以得到多值解的性质称为解的多值性,随着系统参数或激励频率的连续变化,系统振动的位移、速度等参数发生突然的变化称为跳跃现象。HCR和LCR齿轮系统啮合线的位移跳跃现象如图5和图6所示。
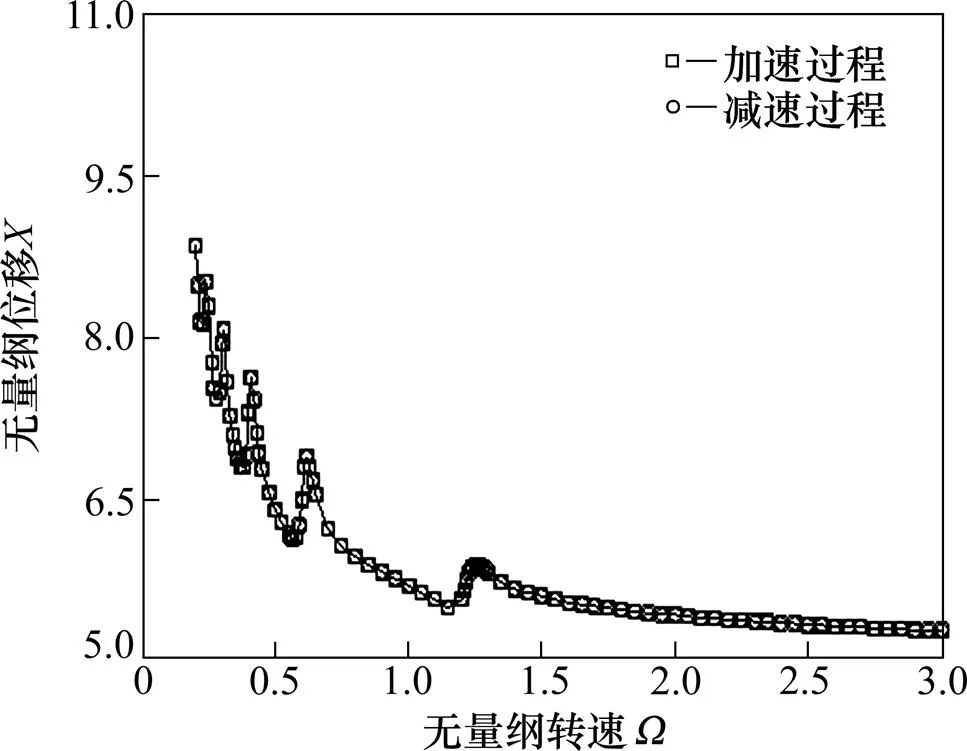
图5 转速对HCR齿轮啮合线位移跳跃的影响
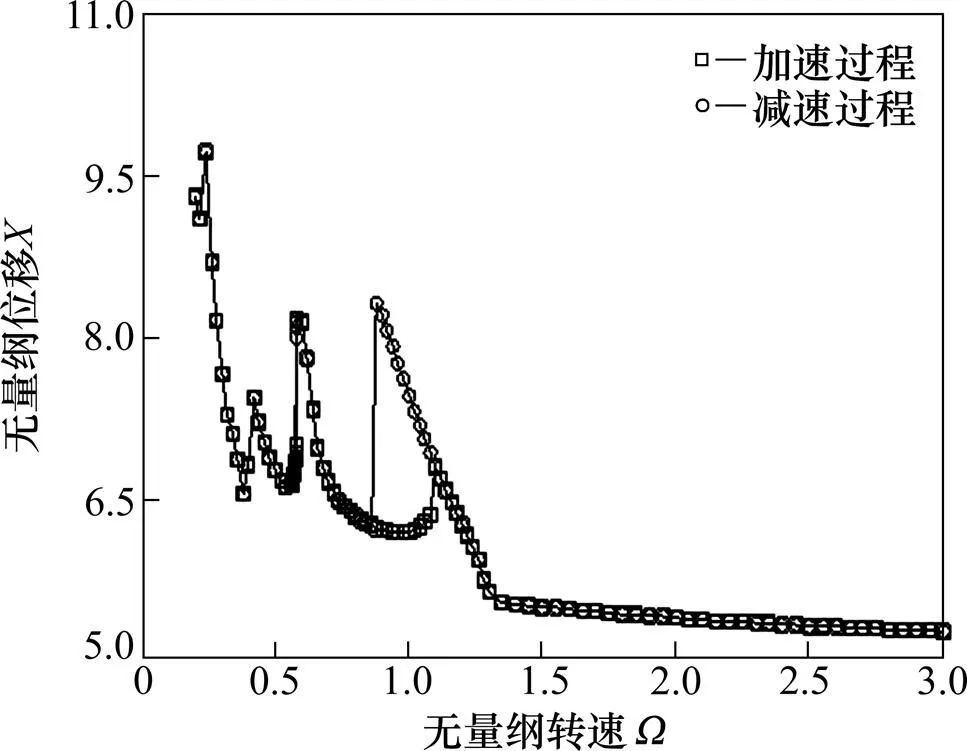
图6 转速对LCR齿轮啮合线位移跳跃的影响
由图5和图6可知,HCR齿轮啮合线位移连续,未发生明显的跳跃,齿轮的运动状态未发生明显改变,与图3表现的规律相同;而LCR齿轮的啮合线位移在转速为0.57~0.58和0.86~1.15处发生了明显的振动位移跳跃,在=2.42时系统发生不明显的跳跃现象。
由于啮合线位移振动的跳跃造成了系统的运动的不稳定性,在跳跃点时,系统会因为运行参数的轻微变化,振动的强度会发生较大改变,使系统运动状态发生改变,对齿轮系统的运行将造成不利影响。
3 误差对齿轮转速分岔特性的影响
误差对系统的动力学特性有较大的影响,齿轮的误差激励主要由齿频误差激励、偏心误差激励组成;齿频误差激励由基节误差、齿形误差、齿厚误差等与齿频相关的误差在啮合线上的投影组成;偏心误差激励为转动周期误差激励,其主要为各个齿轮的偏心误差在啮合线上的投影;为各齿频误差在啮合线上的投影矢量和;g和P分别为齿轮g和齿轮p的安装误差在啮合线上的投影。
3.1 齿频误差对齿轮分岔特性的影响
取无量纲齿频误差激励=1,即齿频误差激励为10 μm,其他误差g=0,p=0;对含齿频误差激励的HCR齿轮和LCR齿轮系统随着转速的分岔特性进行研究,齿轮系统的啮合阻尼比取0.035,无量纲齿侧间隙为5,即齿侧间隙为50 μm时,HCR和LCR齿轮系统的啮合线位移,随无量纲转速变化的分岔特性如图7和图8所示。
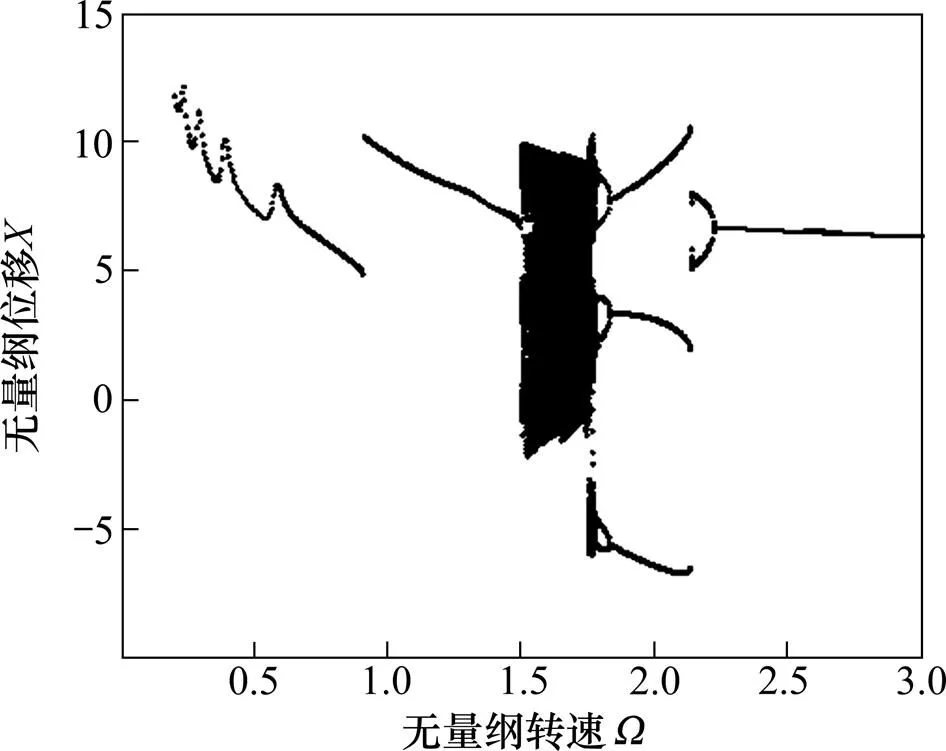
图7 齿频误差对HCR分岔影响
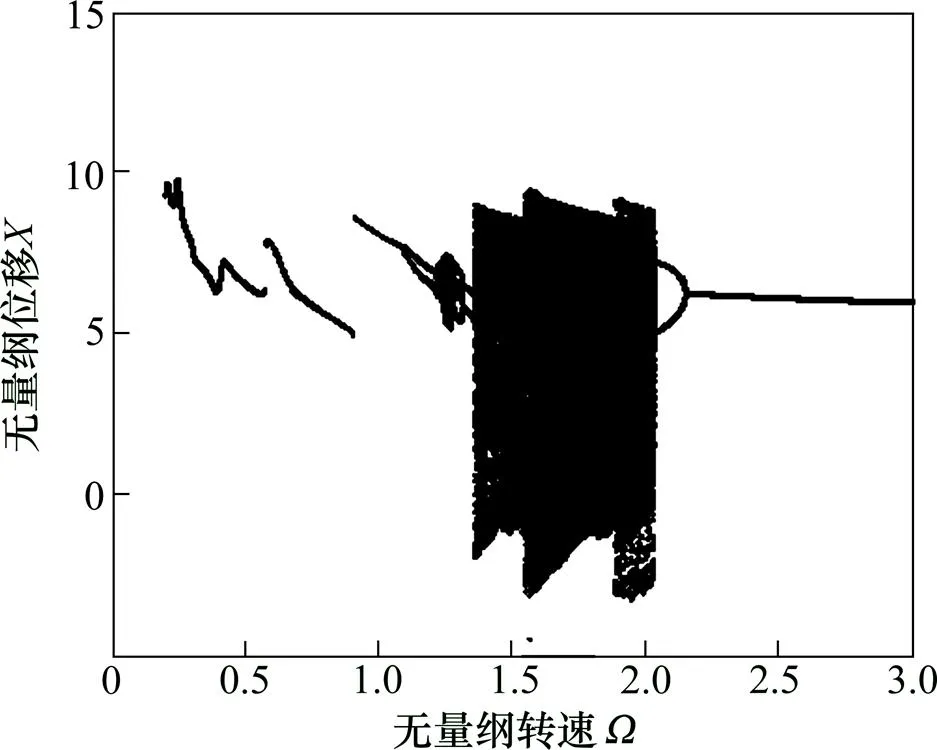
图8 齿频误差对LCR分岔影响
由图7和图8可知:当存在齿频误差影响时,齿轮系统具有丰富的分岔特性;低转速时,齿频误差对齿轮系统的运动状态影响较小,但是高重合度齿轮在共振区域发生了较大的跳跃现象,同时,LCR齿轮在无误差时跳跃点的跳跃幅度增加;“激变”是齿轮系统进入混沌的主要途径[16],高转速时齿频误差对齿轮系统的分岔特性产生了较大的影响,HCR齿轮啮合线的相对位移在高转速时,由单周期运动“激变”进入混沌运动,然后通过激变退出混沌运动状态,经过倒分岔进入6周期、3周期、2周期和单周期运动。LCR齿轮受到的影响较HCR齿轮更突出,系统由单周期运动,经过多次倍分岔运动进入长周期运动,经过短暂的长周期运动经过倒分岔由2周期运动“激变”进入较大转速范围的混沌运动,最后系统由混沌运动状态经过倒分岔进入2周期和单周期运动。
齿频误差激励对LCR齿轮在较大转速范围内动力学特性产生较大影响,齿轮系统混沌区域的转速范围较HCR齿轮要大的多,因此HCR齿轮对转速的周期稳定性要优于普通齿轮。由于跳跃和混沌运动加剧齿轮系统的振动和噪声,相对低重合度齿轮,高重合度齿轮可以有效降低齿轮系统的振动和噪声。
3.2 偏心误差对齿轮系统分岔特性影响
将齿频误差激励设定为=0,齿侧间隙保持不变,对HCR齿轮和LCR齿轮随着偏心误差变化的分岔特性进行研究,齿轮系统的啮合阻尼比取0.035,齿轮的无量纲安装误差g=2和P=2,即安装误差为20 μm。图9和图10所示为HCR的LCR齿轮系统的啮合线位移随无量纲转速变化的分岔特性。
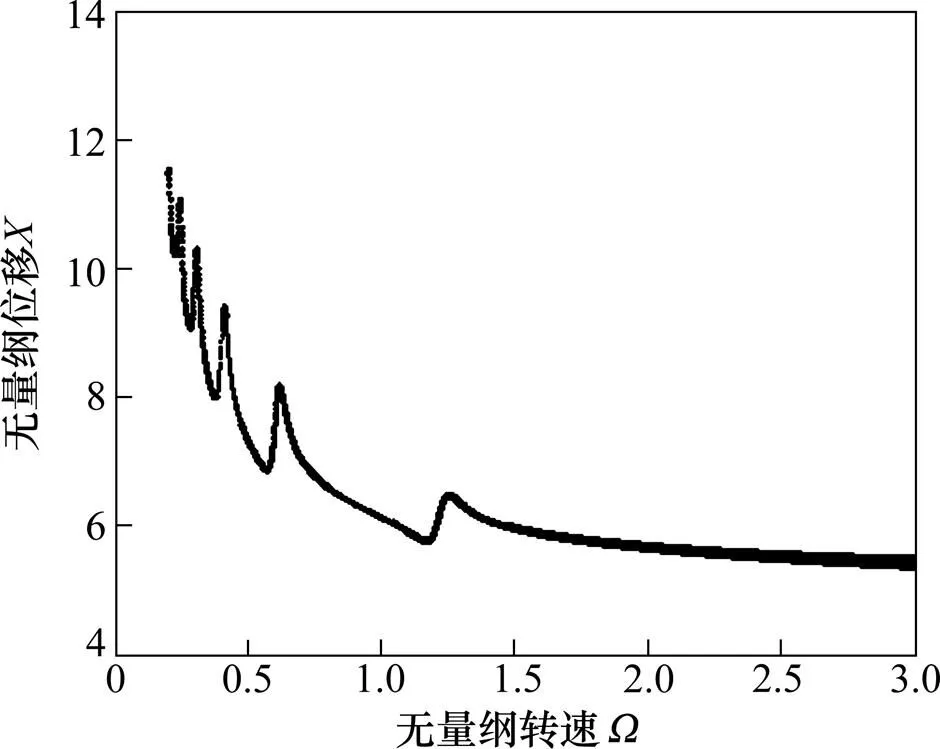
图9 偏心误差对HCR分岔影响
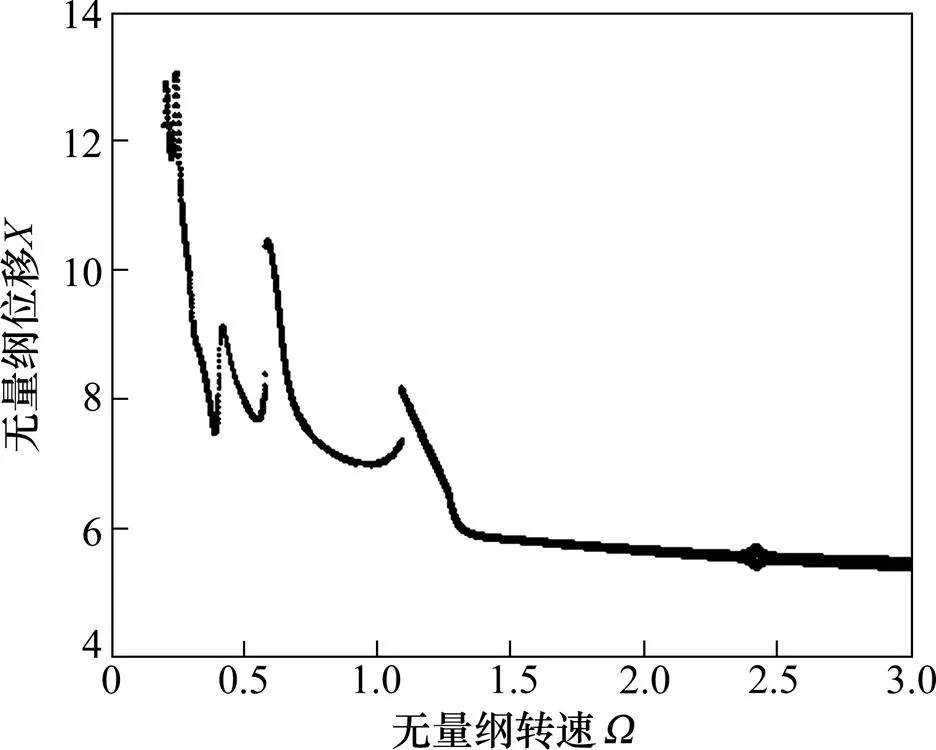
图10 偏心误差对LCR分岔影响
由图9和图10可知:当齿轮的偏心误差增加时,齿轮啮合线位移的幅值变大,HCR齿轮啮合线位移的解稳定域变宽,但其周期运动规律未发生改变,系统的分岔特性没有发生本质改变。偏心误差对LCR齿轮啮合线位移跳跃影响较大,系统的跳跃幅值增加,加剧齿轮的振动,在无量纲转速=2.42时,系统发生分岔现象。
当无量纲转速=2.42时,系统的啮合线无量纲位移随误差增加的分岔特性如图11~14所示。

图11 HCR齿轮随主动齿轮偏心误差分岔
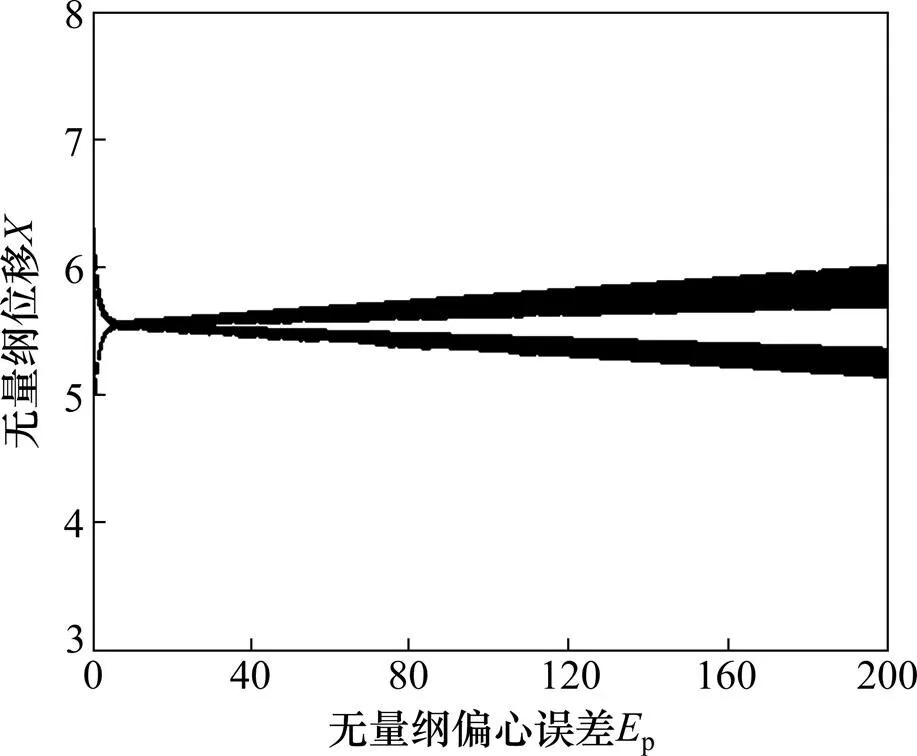
图12 LCR齿轮随主动齿轮偏心误差分岔
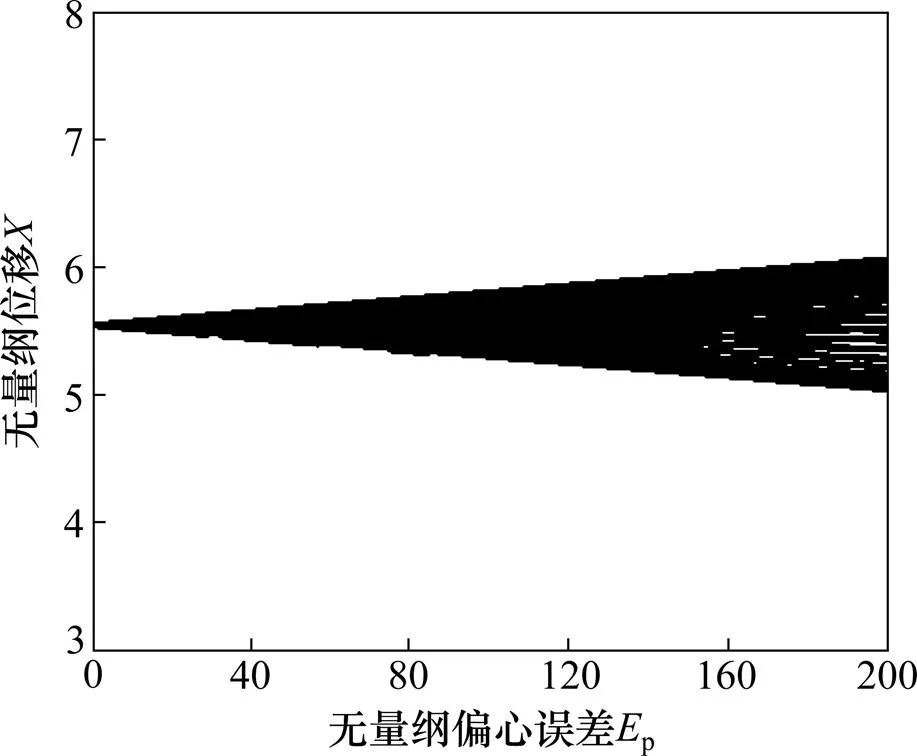
图13 HCR齿轮随从动齿轮偏心误差分岔
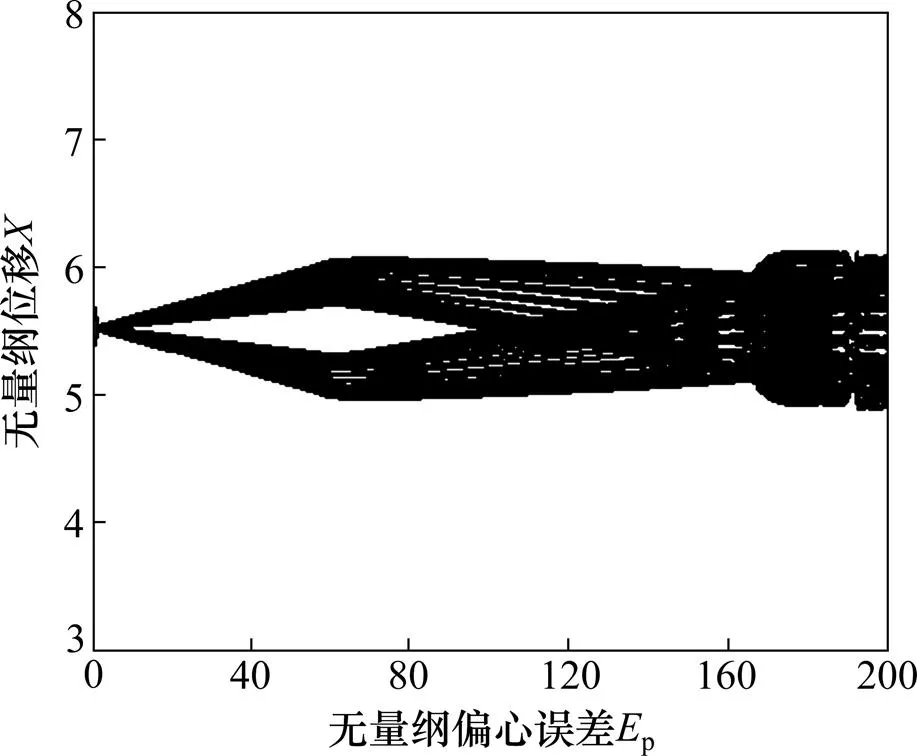
图14 LCR齿轮随从动齿轮偏心误差分岔
由图11~14可知:随着偏心误差的增加,系统的周期稳定性区域逐渐变大,齿轮的啮合线的位移变动范围变大。在该转速下偏心误差对LCR齿轮的影响相对HCR齿轮影响要大;随着偏心误差的增加,HCR齿轮的运动状态没有发生改变,仅发生周期扩散现象, 其总体作单周期运动,而LCR齿轮的运动状态发生了较大的变化,其经过倒分岔和分岔现象,由两周期进入单周期后再次进入两周期,同时周期的扩散要比HCR齿轮的大,从动齿轮较大偏心误差的影响下系统作复杂的无规则运行。
4 结论
1) 当忽略误差影响,仅考虑齿侧间隙的情况下,HCR齿轮系统连续平稳,不存在跳跃现象;LCR齿轮的啮合线的位移在部分转速下发生了跳跃现象,在固有频率附近(无量纲转速为0.57~0.58和0.86~1.15处)发生幅度较大跳跃,因此,HCR齿轮运行相对LCR齿轮运行要平稳。
2) 齿频误差可以增加系统的啮合线位移的振幅,对低速齿轮系统的影响较小,其使HCR齿轮在共振区域发生了跳跃,LCR齿轮在跳跃点的跳跃幅值增加;其对高转速齿轮系统产生较大的影响,齿频误差激励对LCR齿轮在部分高转速区域(无量纲转速为1.1~2.1区域)的动力学影响较为明显,系统混沌区域的影响转速范围要比HCR齿轮的大,HCR齿轮的周期稳定性要比LCR齿轮的更强。
3) 随着偏心误差的增加,齿轮系统的周期稳定性逐渐降低,齿轮的啮合线的位移幅值变大,偏心误差对跳跃点跳跃幅值具有放大作用,偏心误差对LCR齿轮的影响要比HCR齿轮的影响大。
[1] Theodossiades S, Natsiavas S. Non-linear dynamics of gear-pair systems with periodic stiffness and backlash[J]. Journal of Sound and Vibration, 2000, 229(2): 287−310.
[2] Parker R G, Vijayakar S M, Imajo T. Non-linear dynamic response of a spur gear pair: Modelling and experimental comparisons[J]. Journal of Sound and Vibration, 2000, 237(3): 435−455.
[3] Saghafi F. Global bifurcation and chaos analysis in nonlinear vibration of spur gear systems[J]. Nonlinear Dynamics, 2014, 75(4): 783−806.
[4] Tamminana V K, Vijayakar S, Kahraman A. A study of the relationship between the dynamic factors and the dynamic transmission error of spur gear pairs[J]. Journal of Mechanical Design, 2007, 129(1): 75−84.
[5] LI Shuting. Effect of addendum on contact strength,bending strength and basic performance parameters of a pair of spur gears[J]. Mechanism and Machine Theory, 2008, 43: 1557−1584.
[6] Kim W, Yoo H H, Chung J T. Dynamic analysis for a pair of spur gears with translational motion due to bearing deformation[J]. Journal of Sound and Vibration, 2010, 329: 440−4421
[7] WANG Jiande, Howard I. Finite element analysis of high contact ratio spur gears in mesh[J]. Journal of Tribology, 2003, 127: 469−483.
[8] Thirumurugan R G. Critical loading points for maximum fillet and contact stresses in normal and high contact ratio spur gears based on load sharing ratio[J]. Mechanics Based Design of Structures and Machines, 2011, 39: 118−141.
[9] 刘梦军. 单对齿轮系统间隙非线性动力学研究[D]. 西安: 西北工业大学机电学院, 2002.
LIU Mengjun. The backlash nonlinear dynamics characters of single pair gear system study[D]. Xi’an: Northwestern Polytechnical University. School of Mechanical Engineering, 2002.
[10] 刘晓宁, 王三民,沈允文. 三自由度齿轮传动系统的非线性振动分析[J]. 机械科学与技术, 2004, 23(10): 1191−1193.
LIU Xiaoning, WANG Sanmin, SHEN Yunwen. Nonlinear vibrations of 3-dof geared rotor-bearing system[J]. Mechanical Science and Technology, 2004, 23(10): 1191−1193.
[11] 赵宁, 杨杰. 高重合度圆柱齿轮传动多目标优化设计[J]. 机械传动, 2012, 36(7): 43−46.
ZHAO Ning, YANG Jie. Multi-objective optimization design of high contact ratio cylindrical gear drive[J]. Journal of Mechanical Transmission, 2012, 36(7): 43−46.
[12] 渠珍珍, 鲍和云, 朱如鹏. 高重合度行星齿轮系参数优化设计[J]. 机械设计与制造, 2011(12): 41−43.
QU Zhenzhen, BAO Heyun, ZHU Rupeng. Optimal design for parameter of high contact ratio planetary gears system[J]. Machinery Design & Manufacture, 2011(12): 41−43.
[13] 渠珍珍.高重合度行星齿轮传动系统设计及动力学分析[D]. 南京: 南京航空航天大学机电学院, 2011.
QU Zhenzhen.Design and dynamics analysis of high contact ratio planetary gear transmission[D]. Nanjing: Nanjing University of Aeronautics and Astronautic. School of Mechanical Engineering, 2011.
[14] 张祖芳, 陈卫东, 黄康. 重合度对齿轮副非线性动力学特性影响研究[J]. 组合机床与自动化加工技术, 2014(2): 40−43.
ZHANG Zufang, CHEN Weidong, HUANG Kang. Research on effect of contact ratio on non-linear dynamics of spur gear pair[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014(2): 40−43.
[15] 方宗德, 蒋孝煜, 宋镜瀛. 大重合度齿轮的性能研究[J]. 齿轮, 1987, 11(1): 27−32.
FANG Zongde, JIANG Xiaoyu, SONG Jingying. Performance study of high contact ratio gear[J]. Gear, 1987, 11(1): 27−32.
[16] 李同杰, 朱如鹏, 鲍和云, 等. 行星齿轮系扭转非线性振动建模与运动分岔特性研究[J]. 机械工程学报, 2011, 47(21): 76−83.
LI Tongjie, Zhu Rupeng, Bao Heyun, at al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train[J]. Journal of Mechanical Engineering, 2011, 47(21): 76−83.
Contrastive analysis of dynamic bifurcation characteristics between high contact ratio and low contact ratio gears system
LI Fajia, ZHU Rupeng, BAO Heyun, YE Fumin, JIN Guanghu
(Jiangsu Key Laboratory of Precision and Micro-Manufacturing Technology, College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
The nonlinear torsion vibration model of gear system was proposed. Backlashes and time-varying meshing stiffness were taken into consideration. The meshing stiffness of high contact ratio (HCR) and low contact ratio (LCR) gears was obtained by the finite element method. The bifurcation characteristics and jump phenomenon along the line of action were investigated. The results show that when the backlashes and errors are neglected, the displacement along action line of HCR gear system becomes steady and continuous, and without jump phenomenon. However, LCR displacement is broken into two regions. In the range 1.1≤≤2.1, the meshing frequency error produces higher dynamic effect for LCR compared with HCR. With the increase of the eccentricity error and the displacement along the line of action, the system stability is decreased gradually and the eccentricity error has more important effect for LCR than HCR. More importantly, HCR gear system has higher stability and more smooth motion than LCR gears. Finally, HCR gear system can decrease the vibration and noise significantly.
high contact ratio; gear system; dynamics; bifurcation; stability
TH113.1
A
1672−7207(2015)02−0465−07
2014−04−20;
2014−07−15
国家自然科学基金资助项目(51305196);中央高校基本科研业务费专项资金资助项目(NZ2014201)(Project (51305196) supported by the National Natural Science Foundation of China; Project (NZ2014201) supported by the Fundamental Research Funds for the Central University)
朱如鹏,教授,博士生导师,从事机械传动、结构强度、机械CAD及自动化研究;E-mail:rpzhu@nuaa.edu.cn
10.11817/j.issn.1672-7207.2015.02.013
(编辑 赵俊)
