井下弹道式煤矸分选的理论和实验

周甲伟，王福荣，刘瑜，杜长龙



井下弹道式煤矸分选的理论和实验

周甲伟1，王福荣1，刘瑜1，杜长龙2

(1. 河南理工大学 机械与动力工程学院，河南 焦作，454000；2. 中国矿业大学 机电工程学院，江苏 徐州，221116)

为减少矸石山地面污染，对井下弹道式煤矸分选方法进行研究。利用非线性接触模型对煤和矸石的抛射、碰撞和反弹过程进行分析，得到反弹距离理论计算公式，确定其主要影响因素为煤和矸石碰撞前后的接触刚度。对新汶协庄矿的煤和矸石进行反弹距离实验，实验结果表明：煤的反弹距离服从正态分布，矸石的反弹距离服从G分布；当冲击速度大于7 m/s时，二者的反弹距离差值较大，可以分离出约30%的矸石，并且此时部分煤被破碎，可结合破碎粒度分离出更多的矸石。利用实验数据得到煤和矸石反弹距离的拟合公式，其相关系数2分别为0.835和0.918。

煤矸分选；冲击速度；反弹距离；分布；差值；数据拟合

矸石作为煤炭开采的伴生物，在地面堆积形成矸石山，对矿区环境造成严重污染[1−3]。在井下对煤和矸石进行分离，并将矸石就地充填，是减少矸石山污染的根本途径，近些年已成为国内外学者关注的热点研究问题[4−9]。缪协兴等[10]指出对井下矸石的处理包括煤矿巷道掘进矸石以及采掘工作面的煤流矸石2部分。巷道掘进矸石可以直接进行破碎、胶结并就地充填，而煤流矸石则需要先在井下与煤分离再作为充填材料。目前，井下煤和矸石的分离多采用选择性破碎的方法来实现[11−15]。丰建荣等[12−13]采用液压力使煤破碎而矸石不破碎；李建平等[15]通过物料抛射后的冲击力实现煤和矸石的选择性破碎。以上方法都以煤被破碎为前提，会降低煤的粒度，影响煤矿的经济效益。郎庆田等[16−17]提出井下弹道式煤矸分选方法，依据煤和矸石物理机械特性的差异，使二者以相同的初始条件与弹力作用板发生碰撞，并利用其反弹距离差异进行分选。该方法具有能量损耗低、煤块破碎率小、使用成本低等优点，可以保证煤矿的经济效益，但是目前仍处于研究阶段，尚无完善的理论和可靠的实验数据为其可行性提供验证，限制了其工业应用进程。为此，本文作者通过碰撞反弹分析建立反弹距离的理论计算公式，对新汶协庄矿煤和矸石进行反弹距离实验，得到煤和矸石反弹距离的统计分布，并确定二者实现弹道式分选的冲击速度范围，通过实验数据对反弹距离公式进行拟合，以便为冲击速度的初步确定提供依据。

1 弹道式煤矸分选的理论分析

弹道式煤矸分选中煤和矸石获得冲击速度后的运动过程如图1所示，可以分为抛射、碰撞和反弹3个阶段。煤或矸石自点被抛出直至在点接触弹力作用板之前为抛射阶段，自点与弹力作用板发生碰撞至离开弹力作用板为碰撞阶段，自离开弹力作用板至落在地面点为反弹阶段。

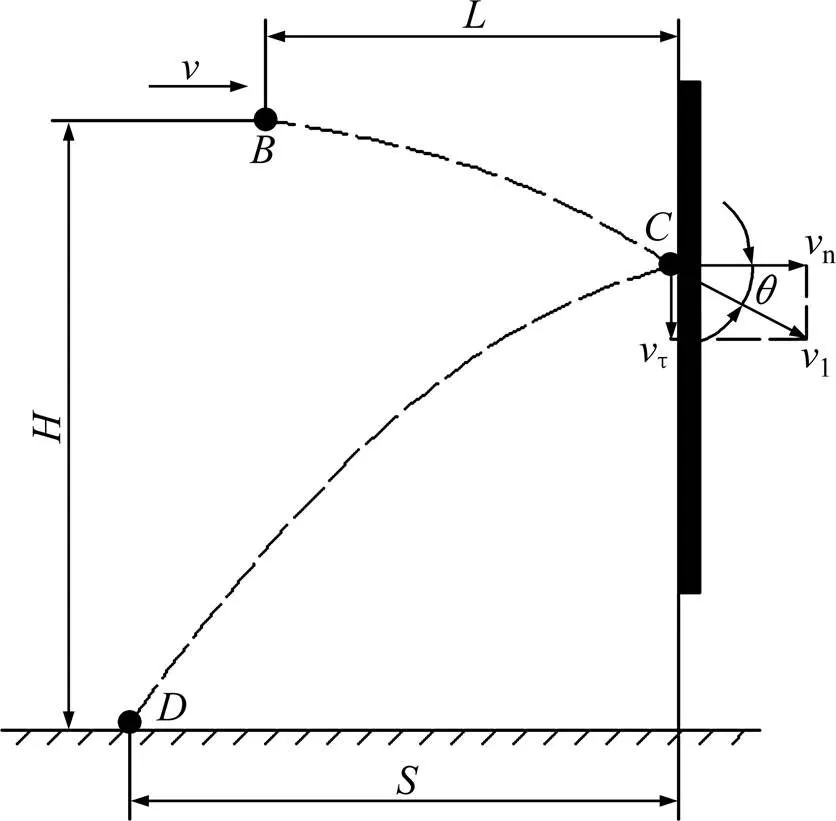
图1 弹道式煤矸分选的运动过程

为便于理论分析，本研究基于以下假设：1) 假设整个碰撞过程中煤和矸石均不发生破碎；2) 忽略煤和矸石的形状因素，假设其均为球形颗粒，以下简称颗粒；3) 假设弹力作用板为刚体；4) 忽略空气阻力以及摩擦力的影响，不考虑颗粒与弹力作用板的黏连。

1.1 抛射阶段

根据假设可知，颗粒在抛射阶段只受自身的重力作用，则颗粒到达点时的水平和竖直速度分量分别为

式中：为颗粒抛射时的初速度；n和分别为颗粒到达点时的水平和竖直速度分量；为重力加速度；为抛射点距弹力作用板的水平距离。

1.2 碰撞阶段

颗粒在点与弹力作用板的碰撞过程可以分为压缩和恢复2个阶段，二者在颗粒变形量达到最大时转变。根据假设，在碰撞过程中只需考虑水平方向速度分量n的作用。由于煤和矸石内部存在裂隙，在与弹力作用板的碰撞过程中裂纹被压密，因此，碰撞结束后会产生一定的残余变形量，使得恢复阶段与压缩阶段具有不同的接触刚度。所以，选择非线性接触模 型[18]描述弹道式煤矸分选的碰撞过程：

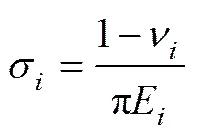
式中：()为接触力；为颗粒碰撞过程中的变形量；y为压缩阶段的接触刚度，由于，故接触刚度可表示为；E，和r分别为颗粒和弹力作用板的弹性模量、泊松比和接触半径；下标“1”表示颗粒，下标“2”表示弹力作用板；f为恢复阶段的接触刚度，与颗粒材料参数以及冲击速度有关；0为颗粒的残余变形量。

根据弹性力做功原理，在压缩阶段和恢复阶段分别有

式中：为颗粒质量；n′为碰撞阶段结束后颗粒的水平速度；为颗粒碰撞阶段最大变形量。

引入碰撞恢复系数，定义为碰撞后与碰撞前颗粒速度之比，由式(3)可得：

在碰撞压缩结束和恢复开始时，颗粒变形量达到最大值，两阶段的接触力相等，即

式中，max为碰撞阶段的最大接触力。

结合式(4)~(6)有：

1.3 反弹阶段

根据忽略空气阻力和摩擦力的假设，颗粒碰撞阶段前后的竖直速度分量不变。颗粒在反弹阶段落至点时距弹力作用板的距离为

式中：为颗粒的反弹距离；为抛射点距地面的高度。由式(9)可知，颗粒的反弹距离与碰撞前后的接触刚度有关，煤和矸石的物理机械性质存在差异，二者的接触刚度也不相同，这表明煤和矸石的弹道式分选在理论上具有可行性。

2 反弹距离实验设计及实验结果

2.1 反弹距离实验设计

测量煤和矸石反弹距离的实验在自行研制的反弹距离实验台上进行。该实验台由冲击速度实现装置和数据采集两部分组成，其原理如图2所示。冲击速度实现装置由弹射车、弹射轨道、胶乳胶带和阻尼弹簧组成，弹射车装载物料在胶乳胶带的作用下进行加速，当遇到阻尼弹簧时，弹射车的速度逐渐减小，物料以原速度被弹射出去。数据采集包括冲击速度采集和反弹距离测量。用轴编码器采集冲击速度信号，将其通过单片机传输至计算机，并转化为直线冲击速度在界面输出，用钢尺人工测量物料落地点距弹力作用板的直线距离为反弹距离。

1—计算机；2—单片机；3—轴编码器；4—抛射轨道；5—抛射车；6—胶乳胶带；7—阻尼弹簧

2.2 实验材料

选择新汶协庄矿的煤和矸石进行反弹距离实验，实验的抛射点高度为870 mm，抛射点距反弹板的水平距离为1 000 mm。

2.3 实验结果

共实验有效煤232块，有效矸石186块。根据实验情况，将煤和矸石的粒度以及冲击速度分别划分为4个水平，煤和矸石在不同水平下的反弹距离平均值见表1和表2，表中括号内的数值为在该水平内进行实验的煤或矸石的数量，括号外的数值则为该水平内实验煤或矸石的反弹距离平均值。

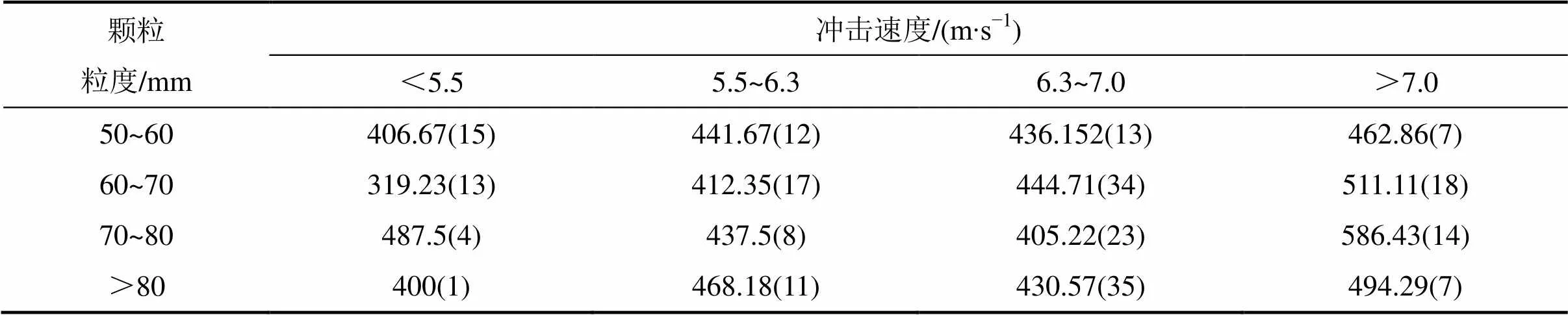
表1 协庄矿煤的反弹距离平均值

表2 协庄矿矸石的反弹距离平均值

3 分析与讨论

3.1 煤和矸石的反弹距离分布

根据表1中实验数据用MATLAB软件绘制有效煤的反弹距离分布直方图，并对其进行正态分布拟合，结果如图3所示，该曲线的特征方程为

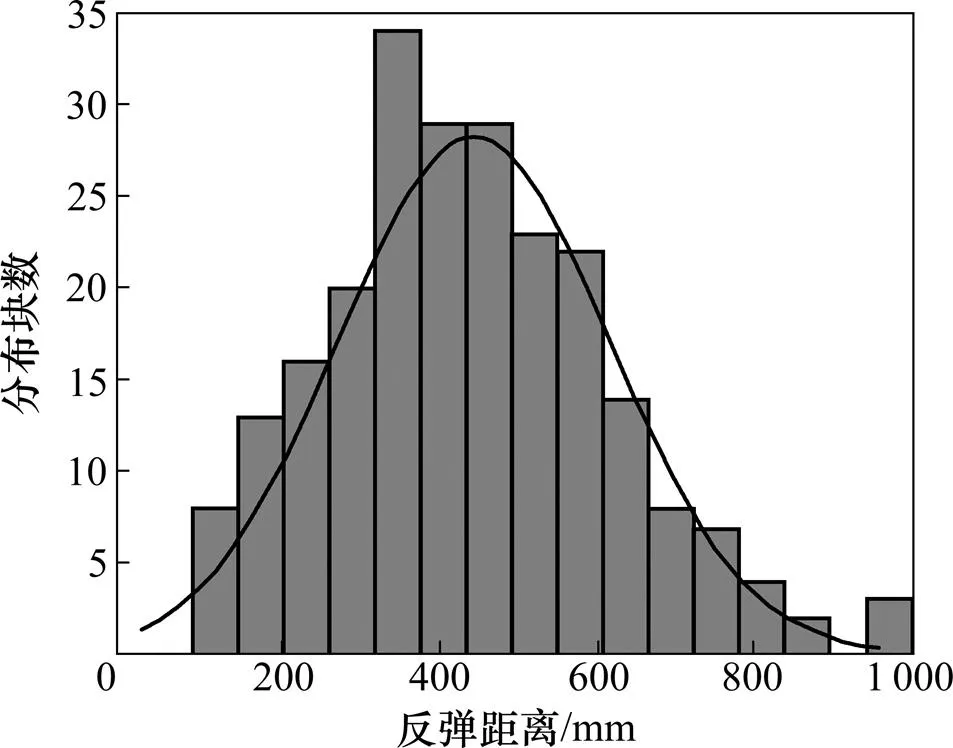
图3 全部煤反弹距离分布

对该分布进行jarque-Bera检验，返回值为“0”，表明实验煤颗粒的反弹距离符合(443.32，173.062)分布。

同样，依据表2中实验数据绘制有效矸石的反弹距离分布直方图并对其进行正态分布拟合，如图4所示。对应特征方程的jarque-Bera检验返回值为“1”，表明实验矸石颗粒的反弹距离不符合正态分布。图4中的直方图分布呈现出一定的偏斜，因此，采用具有不对称性的分布对其反弹距离进行统计分析。图4中，分布曲线的特征方程为

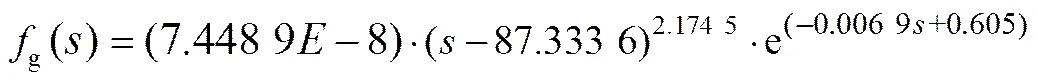
对该分布进行2拟合检验，结果表明：该数据数据服从G分布，且计算偏态系数s为1.122 5，大于0，说明G分布呈右偏斜，与图4中的分布曲线相吻合。

1—正态分布；2—Γ分布

3.2 煤和矸石反弹距离差异

实验煤和矸石反弹距离的概率分布如图5所示。图中阴影部分为矸石反弹距离大于煤反弹距离的概率，即可以分离出矸石的概率。由图5可知：对实验煤和矸石而言，反弹距离均值相差不大，在全部实验冲击速度范围内依靠反弹距离可分离的矸石数量有限；但是实验煤的反弹距离都小于1 m，而部分实验矸石的反弹距离大于1 m，根据理论分析可知反弹距离是冲击速度的函数，若调整冲击速度使大量矸石的反弹距离大于1 m，则可能分选出更多的矸石。

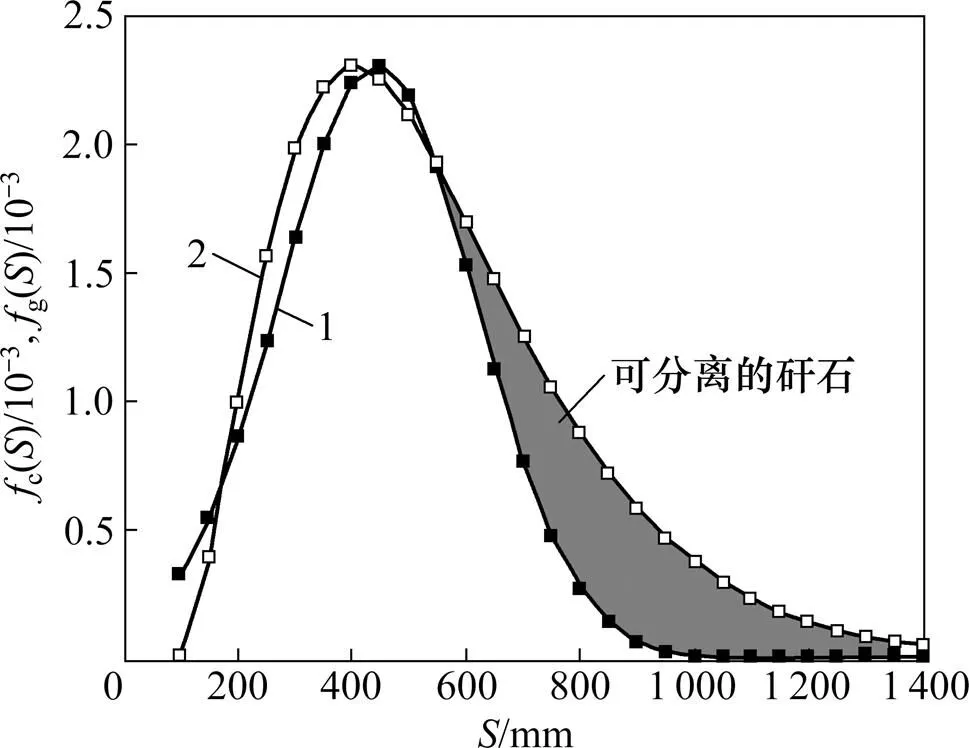
1—fc(S)；2—fg(S)

图6所示为不同粒度范围内煤和矸石的反弹距离平均值。由图6可知，煤和矸石反弹距离平均值与冲击速度相关，二者在冲击速度较高时具有较大差值。当冲击速度较低时 (7.0 m/s以下)，煤和矸石基本没有破碎，弹力作用都以反弹为主，其恢复系数均近似常数，二者反弹距离的差值及其变化都较小；当冲击速度较高时(7.0 m/s以上)，煤发生破碎，出现能量耗散，恢复系数骤减，而矸石破碎较少，恢复系数与原来变化不大，故反弹距离差值增大。

1—煤块；2—矸石

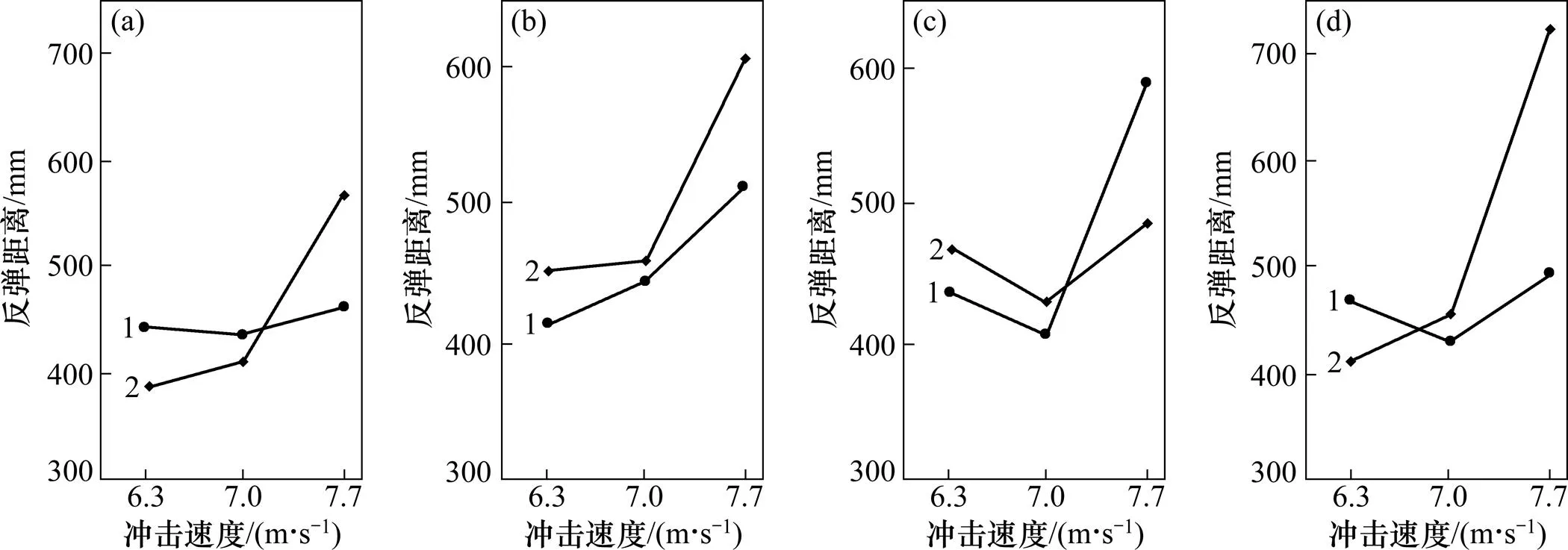
根据上述分析，破碎会对反弹距离的变化趋势产生影响。在煤发生破碎而矸石未破碎的情况下，二者的反弹距离差值大于两者都不破碎时的反弹距离差值。将全部矸石的反弹距离与对应速度下破碎煤的反弹距离相比较，并进行最小二乘法拟合，结果见图7。

冲击速度/(m∙s−1)：(a) ＜6.3；(b) 6.3~7.0；(c) ＞7.0

由图7可知：1) 冲击速度小于6.3 m/s时，二者的反弹距离呈交错状态，煤和矸石反弹距离分布并无明显的分区特征，在此冲击速度范围内难以实现反弹距离分选。2) 冲击速度在6.3~7.0 m/s时，部分煤发生破碎，煤的反弹距离仍然呈上升趋势，煤具有最大平均反弹距离。矸石的反弹距离开始随冲击速度的增大而持续增大，并且反弹距离大的以矸石为主。但是煤和矸石反弹距离尚无明显的分选界限。3) 冲击速度在7.0~7.7 m/s时，大部分煤发生破碎，煤的反弹距离有明显的下降趋势。而矸石的反弹距离仍随冲击速度增大而增大，煤和矸石的反弹距离差值也随冲击速度增大而增加，即在该阶段实现反弹距离分选具有可行性。

结合上述现象，对所有煤和矸石的反弹距离进行分析，发现当冲击速度大于7.0 m/s时，共实验煤31块，而反弹距离大于800 mm的仅有1块；共实验矸石块85块，反弹距离大于800的有25块。当冲击速度大于7.0 m/s时，依靠反弹距离可以分选出矸石约30%，而丢煤率为3%，并且此时未破碎的煤大部分存在夹矸现象。若将弹道式分选和选择性破碎分选相结合，则能分选出更多的矸石。

3.3 实验煤和矸石的反弹距离公式

由式(9)可知：反弹距离仅与冲击速度以及颗粒自身的材料参数有关。对于实验用煤和矸石，将其材料参数视为常数，则恢复系数可以表示为

式中：为常系数；()为冲击速度的函数。

将式(12)与实验参数和均代入式(9)，则

一般函数均可通过泰勒展开表示为多项式的形式，令()=12+2+0(1，2和0为常系数)，采用多项式拟合的方法确定实验煤和矸石的反弹距离公式。

将实验煤和矸石的冲击速度以0.2 m/s的区间分开，并计算区间内的反弹距离平均值，其结果如表3和表4所示，表中的冲击速度为各区间的速度中值。分别对表3和表4中的实验数据进行拟合，得到新汶协庄矿煤和矸石颗粒的反弹距离公式为：

式中：c为新汶协庄矿煤的反弹距离；g为新汶协庄矿矸石的反弹距离。

表3 实验煤的反弹距离

表4 实验矸石的反弹距离

新汶协庄矿煤和矸石反弹距离与冲击速度的关系如图8所示。煤和矸石反弹距离拟合曲线的相关系数2分别为0.835和0.918，均具有较高的拟合精度，可用于该矿弹道式煤矸分选时冲击速度的初步确定。

(a) 新汶协庄矿煤；(b) 新汶协庄矿矸石

4 结论

1) 在理论上对依据煤和矸石抛射后反弹距离差异实现分选的弹道式煤矸分选方法进行分析，基于非线性接触模型得到颗粒与弹力作用板碰撞后的反弹距离公式，明确反弹距离的影响因素为冲击速度和颗粒的材料参数。煤和矸石的物理机械性质差异决定了二者在相同冲击速度下的反弹距离也存在差值，为弹道式煤矸分选提供了理论依据。

2) 煤的反弹距离服从正态分布，矸石的反弹距离服从分布，二者的反弹距离均值差异不大；但是实验煤的反弹距离都小于1 m，而部分实验矸石的反弹距离大于1 m，若调整冲击速度使大量矸石的反弹距离大于1 m，则可能实现煤和矸石的分选。

3) 对新汶协庄矿煤和矸石而言，当冲击速度小于7 m/s时，煤和矸石基本没有破碎，恢复系数均近似常数，二者的反弹距离差值较小，无法实现煤和矸石的分选；当冲击速度大于7 m/s时，煤发生破碎，恢复系数减小，而矸石破碎较少，恢复系数与原来变化不大，二者的反弹距离差值增大，按照反弹距离能够分离出部分矸石，并且煤破碎导致粒度减小，若结合破碎粒度，可以分离出更多的矸石。

4) 对实验煤和矸石的反弹距离进行数据拟合，得到由冲击速度表示的新汶协庄矿煤和矸石反弹距离公式，可以用于该矿弹道式煤矸分选中冲击速度的初步确定。

[1] 敖卫华, 黄文辉. 内蒙古乌达矿区矸石山对生态环境的影响[J]. 煤炭学报, 2005, 30(5): 656−660.
AO Weihua, HUANG Wenhui. Effect of the waste dump on environmental in Wuda mining area inner Mongolia[J]. Journal of China Coal Society, 2005, 30(5): 656−660.

[2] SUN Yuzhuang, FAN Jingsen, QIN Peng, et al. Pollution extents of organic substances from a coal gangue dump of Jiulong Coal Mine, China[J]. Environ Geochem Health, 2009, 31(1): 81−89.

[3] FU Tianling, WU Yonggui, OU Lisha, et al. Effects of thin covers on the release of coal gangue contaminants[J]. Energy Procedia, 2012, 16: 327−333.

[4] 余伟健, 高谦. 充填采矿优化设计中的综合稳定性评价指标[J]. 中南大学学报(自然科学版), 2011, 42(8): 2475−2484.
YU Weijian, GAO Qian. Stability evaluation indexes in optimization design of filling mining[J]. Journal of Central South University (Science and Technology), 2011, 42(8): 2475−2484.

[5] 郭忠平, 黄万朋. 矸石倾斜条带充填体参数优化及其稳定性分析[J]. 煤炭学报, 2011, 36(2): 234−238.
GUO Zhongping, HUANG Wanpeng. Parameter optimization and stability analysis of inclined gangue strip-fillings[J]. Journal of China Coal Society, 2011, 36(2): 234−238.

[6] MIAO Xiexing, ZHANG Jixiong, FENG Meimei. Waste-filling in fully-mechanized coal mining and its application[J]. Journal of China University of Mining and Technology, 2008, 18(4): 479−482.

[7] 何哲祥, 隋利军, 解伟. 矿山充填料管道挤压输送计算机模拟[J]. 中南大学学报(自然科学版), 2008, 39(6): 1144−1151.
HE Zhexiong, SUI Lijun, XIE Wei. Computer simulation of squeezed-transport of mine hydraulic filling in pipeline[J]. Journal of Central South University (Science and Technology), 2008, 39(6): 1144−1151.

[8] ZHU Jianming, MA Zhongwen, XU Jinhai, et al. Research on the technology of filling and repeated mining in thick coal seam affected by small mine gob area[J]. Procedia Engineering, 2011, 26: 1150−1156.

[9] YANG Guoliang, YANG Renshu, TONG Qiang, et al. Coalmine green mining with gangue backfilling technique[J]. Procedia Environmental Sciences, 2011, 10: 1205−1209.

[10] 缪协兴, 钱鸣高. 中国煤炭资源绿色开采研究现状与展望[J]. 采矿与安全工程学报, 2009, 26(1): 1−14.
MIAO Xiexing, QIAN Minggao. Research on green mining of coal resources in China: current status and future prospects[J]. Journal of Mining and Safety Engineering, 2009, 26(1): 1−14.

[11] 丰建荣. 煤和矸石井下破碎分选理论及实验研究[D]. 太原: 太原理工大学矿业工程学院, 2006: 1−13.
FENG Jianrong. Theoretical and experimental study on selective crashing and separation of coal and gangue below ground[D]. Taiyuan: Taiyuan University of Technology. School of Mining Engineering, 2006: 1−13.

[12] 丰建荣, 刘志河, 李志宏, 等. 煤和矸石静态破碎差别的实验研究[J]. 太原理工大学学报, 2006, 37(1): 42−43, 47.
FENG Jianrong, LIU Zhihe, LI Zhihong, et al. Experimental study on the critical parameter on the crush of mixture of coal and gangue[J]. Journal of Taiyuan University of Technology, 2006, 37(1): 42−43, 47.

[13] 董长双, 姚平喜, 刘志河. 井下煤和矸石液压式自动分选技术[J]. 煤炭科学技术, 2007, 35(3): 54−56.
DONG Changshuang, YAO Pingxi, LIU Zhihe. Hydraulic automatic separation technology of coal and refuse in underground mine[J]. Coal Science and Technology, 2007, 35(3): 54−56.

[14] LI Jianping, DU Changlong, BAO Jianwei. Direct-impact of sieving coal and gangue[J]. Mining Science and Technology, 2010, 20(4): 611−614.

[15] 李建平, 杜长龙, 徐龙江. 煤和矸石的冲击式破碎分离试验[J]. 煤炭学报, 2011, 36(4): 687−690.
LI Jianping, DU Changlong, XU Longjiang. Impactive crushing and separation experiment of coal and gangue[J]. Journal of China Coal Society, 2011, 36(4): 687−690.

[16] 郎庆田, 周甲伟, 王元仁, 等. 基于运动分析和仿真的井下弹道式煤矸分选研究[J]. 煤炭科学技术, 2008, 36(2): 85−87.
LANG Qingtian, ZHOU Jiawei, WANG Yuanren, et al. Study on ballistic separation of coal and refuse based on kinematic analysis and simulation[J]. Coal Science and Technology, 2008, 36(2): 85−87.

[17] 周甲伟, 杜长龙, 刘瑜. 弹道式煤矸分选中煤矸石恢复系数的数值计算[J]. 煤炭科学技术, 2008, 36(10): 65−67.
ZHOU Jiawei, DU Changlong, LIU Yu. Numerical calculation on coal refuse recovery coefficient in ballistic coal and coal refuse separation[J]. Coal Science and Technology, 2008, 36(10): 65−67.

[18] 秦志英, 赵月静, 侯书军. 物料冲击破碎过程的一种非线性力模型[J]. 振动与冲击, 2006, 25(2): 35−37, 182.
QIN Zhiying, ZHAO Yuejing, HOU Shujun. Nonlinear force model during material’s impact crushing[J]. Journal of Vibration and Shock, 2006, 25(2): 35−37, 182.

Theoretical and experimental research on ballistic separation for coal and gangue underground

ZHOU Jiawei1, WANG Furong1, LIU Yu1, DU Changlong2

(1. School of Mechanical and Power Engineering, Henan Polytechnic University, Jiaozuo 454000, China;2. School of Mechanical and Electrical Engineering, China University of Mining and Technology, Xuzhou 221116, China)

In order to reduce the ground pollution caused by gangue dump, the ballistic separation for coal and gangue underground was investigated. The theoretical calculation formula of rebound distance was derived by analysis on projecting, impact and rebound of coal and gangue with nonlinear contact model. The main influence factors of rebound distance are contact stiffness of coal and gangue before and after impact. The rebound distance experiment results of coal and gangue in Xiezhuang mine show that rebound distance of coal is a normal distribution while that of gangue is a gamma distribution. When the impact velocity is higher than 7 m/s, there is about 30% gangue to be separated by the difference of rebound distance. And because the coal is partly crushed, more gangue can be separated in combination with crushing granularity. The fitting formulae of rebound distance for coal and gangue were obtained with experimental data. The correlation coefficient2of the fitting formula for coal is 0.835 while that for gangue is 0.918.

separation for coal and gangue; impact velocity; rebound distance; distribution; difference; data fitting

TD461

A

1672−7207(2015)02−0498−07

2014−02−13；

2014−04−20

江苏省高校科研成果产业化推进项目(JHB2011-31)；河南理工大学博士基金资助项目(B2012-040)(Project (JHB2011-31) supported by the College Industrialization Project of Jiangsu Province; Project (B2012-040) supported by the Doctor Foundation of Henan Polytechnic University)

刘瑜，博士，讲师，从事井下煤矿分离研究；E-mail：hsifsmall@163.com

10.11817/j.issn.1672-7207.2015.02.018

(编辑 赵俊)