深海履带车的路径跟踪控制算法
2015-09-24韩庆珏刘少军
韩庆珏,刘少军
深海履带车的路径跟踪控制算法
韩庆珏,刘少军
(中南大学 机电工程学院,深海矿产资源开发利用技术国家重点实验室,湖南 长沙,410083)
建立深海履带车运动学和路径偏差模型,并针对履带车在工作环境中出现的路径偏差问题提出一种新的路径跟踪算法。基于履带车的行走动力约束,路径跟踪算法中引入线速度和角速度中间变量,避免了由于履带车驱动轮角速度突然变化所导致的系统失稳。同时,为提高系统的响应时间,算法中增加与PID控制类似的比例环节,利用李雅普诺夫法证明控制系统的稳定性,并对深海采矿2种典型期望工作路径的路径跟踪进行仿真。研究结果表明:所提出的新的路径跟踪算法具有良好的快速性和稳定性,能够满足深海采矿履带车的行走控制要求,保证履带车良好的行走性能。
深海;履带车;路径跟踪;算法
对于深海6 km多金属结核及钴结壳采矿领域而言,世界各国相继研制出包含海底履带式采矿车的深海采矿系统[1]。近年来,深海履带车系统作为整个深海采矿系统的核心之一成为各国研究的热点。由于受到海底极其稀软底质特点以及海底洋流等环境因素的影响,深海履带式采矿车的行走控制较困难。为使采矿车能准确按照预定开采路径进行海底作业,采用合理高效的路径跟踪控制算法显得尤为关键。Herber 等[2]对非线性移动机器人的稳定性进行了研究。Endo等[3]利用测距法对小型履带车辆进行路径跟踪控制研究;Keiji等[4]在考虑打滑的情况下利用陀螺仪提高了测距法路径跟踪控制的准确性;Zhou等[5]利用非线参数估计法提出了基于滤波器的跟踪算法。徐俊艳等[6]提出了双曲正切特征曲线路径跟踪算法,并用李雅普诺夫方法证明了系统的全局稳定性。但是,这些研究主要针对运动环境相对简单的陆用车辆。深海履带式采矿车行走的环境极其复杂,由于受到海底稀软底质以及海底洋流的影响,其动力学和运动学是研究的热点。Schulte等[7]通过理论分析和大量实验对深海履带式采矿车动力学特性进行了研究。Yeu等[8]设计了PID和增强型PD路径跟踪控制器,并通过对2种控制效果的仿真对比,对软底质环境下履带车的路径跟踪控制进行了研究;之后,Yeu等[9−10]又提出向量跟踪以及LOS视线路径跟踪控制算法,并通过实验验证了算法的可行性。Wang等[11]利用模糊控制理论,提出了连续状态反馈的有限时间深海采矿车路径跟踪控制算法。李力等[12]建立了深海履带式采矿车液压动力系统模型,利用模糊算法对其运动进行了控制。Dai等[13]综合考虑了软底质及洋流的影响,提出了PID算法,实现了对海底履带车的路径跟踪控制。然而,上述研究将深海稀软底质作为影响路径跟踪控制的重要因素,但忽略了采矿车驱动系统自身固有的动力约束对路径跟踪问题的影响。本文作者在深海履带车运动学模型的基础上,提出一种新的路径跟踪算法。算法中引入中间线速度和角速度变量以满足履带车辆实际驱动系统的动力约束。通过对2种典型的采矿路径的仿真分析,得到了比较好的控制效果。
1 深海履带车运动学模型
深海履带车的行走装置是由左、右2条履带构成,其行走动力由履带驱动轮提供。通过调整左、右履带驱动轮的转速可以实现履带车直行和转弯过程。考虑到深海履带车的行走环境,其自由度变化较少,固履带车可以简化为1个二维的车辆运动学问题。在全局坐标系中,选取固定在履带车上的坐标系统来对履带车的运动过程进行描述,如图1所示。
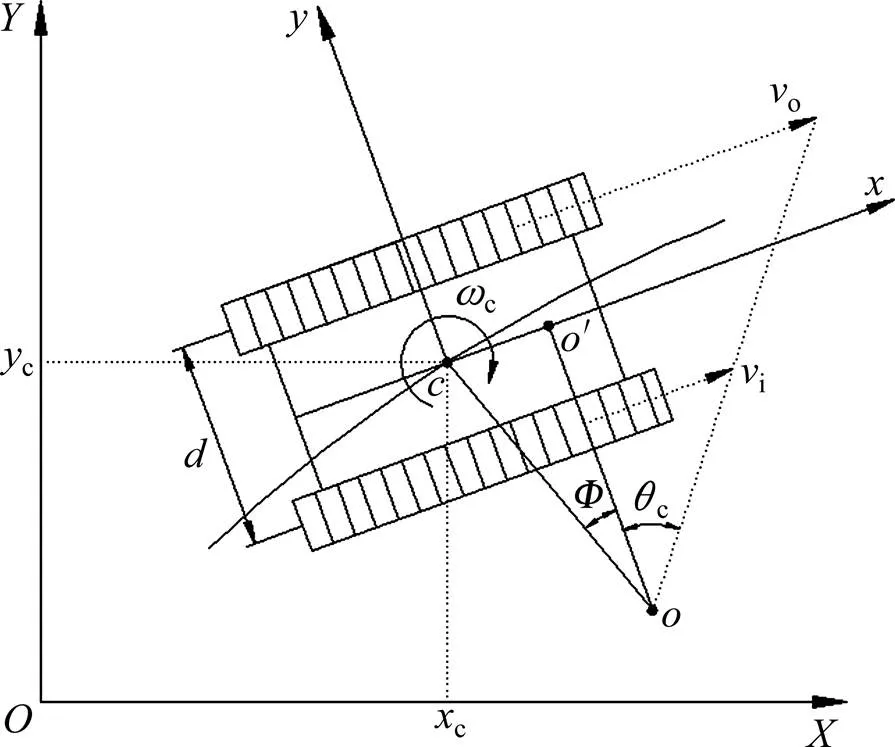
图1 履带车运动学模型
图中:点为履带车运动瞬心;为履带车质量中心;为履带车左右履带的中心距;为侧向打滑角;C履带车的方向角;C为履带车的角速度;i和o分别为内、外侧履带的线速度。在不考虑纵向打滑的情况下,
式中:为履带转动半径;i和o分别为内、外侧履带驱动轮角速度。由此,可以得到履带车的线速度和角速度为:
由图1中的几何关系可知
对于执行深海采矿作业的履带车,由于其行走速度较小(约0.5 m/s),同时其所受的侧向摩擦力很大,因此,假定在履带车转弯过程中由向心力引起的侧向打滑率为0,即图中=0°。则履带车的运动学方程为:
2 深海履带车路径偏差模型
对于深海采矿,为了提高开采效率,在履带车进行开采作业前其开采路径已经基本确定。但在实际采矿过程中,由于布放偏差、海底软底质产生打滑、海底洋流以及与履带车车相连的软管等作用的影响,深海履带车在作业过程中与期望开采路径将会存在一定偏差,其路径偏差模型可用图2表示。图2中:为预定路径;d(d,d,d)为履带车期望位置坐标;C(C,C,C)为履带车当前位置坐标。定义履带车e为当前位置与期望位置的偏差,则e可以通过下式计算得到:
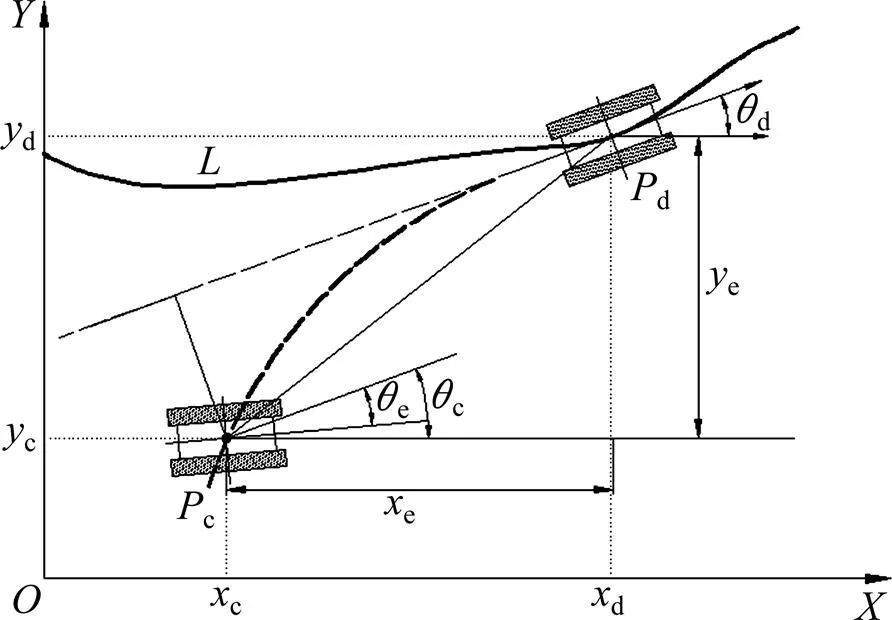
图2 履带车路径偏差模型
同时可以得到路径偏差的导数为
路径跟踪控制问题就是使履带车系统在任意初始位置误差下,确定履带车的输入控制和使得(e,e,e)T有界且lim→∞||(e,e,e)T||=0。
3 履带车行走动力约束
深海履带车在运动过程中,由于自身动力系统性能条件的约束,履带驱动轮的角速度不能随意调整。在控制履带车进行路径跟踪过程中,应该尽量避免驱动轮角速度突然变化情况的发生,否则会导致系统的机械冲击或履带严重打滑,这些都不利于履带车的系统稳定。
设履带车驱动轮角加速度的最大值为max,则履带车行走动力约束条件为
同时,由式(1)~(3)可得
将式(11)中2个式子相加并取导可得
式中:C和C分别为驱动轮的线加速度和角加速度。由式(12)可以看出:驱动轮的角加速度和线加速度约束条件耦合在一起,将最大角加速度平分可以得到独立的角加速度和线加速度约束条件为:
4 路径跟踪算法
由履带车动力约束条件可知,所设计的路径跟踪算法不能使履带驱动轮角加速度超出其最大值;同时,为了保证履带车系统的稳定性,驱动轮的角速度也不应有突然变化。为了满足上述2个条件,在算法中引入驱动轮线速度和角速度判断中间变量j和j:
式中:1,2,3和4为控制系数,均为正值;sgn()为符号函数。在一定的采样周期Δ内,可以将线速度和角速度中间变量转换为加速度中间变量,即
由于式(16)中的加速度参考值是基于动力约束的,所以,将此参考值与集矿机最大线加速度和角加速度进行比较,取较小值作为最终履带车路径跟踪控制输入,得到路径跟踪控制算法为:
在采样周期Δ内,对履带车驱动轮的线速度和角速度进行离散化可以得到路径跟踪的控制方程为
此路径跟踪算法的思想来源于传统的PID控制。传统PID控制中,比例环节对于系统响应的快速性有所改善,所以应予以保留;另外,履带车的动力约束与路径偏差有关,所以,在中间变量中引入max|e|和max|e|。
5 算法稳定性证明
深海履带车路径跟踪控制系统的稳定性要求履带车无论以任何位置为初始条件,系统最终都能跟踪到期望路径上,即系统具有收敛性。选取李雅普诺夫函数
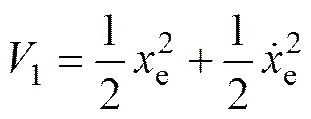
对上式取导得
由式(15)可知:
其中:d为履带车期望位置处的线加速度。将式(21)和(22)代入式(20)得
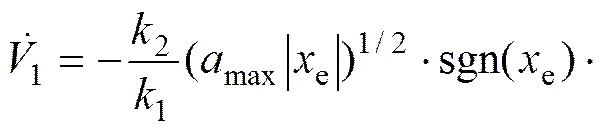
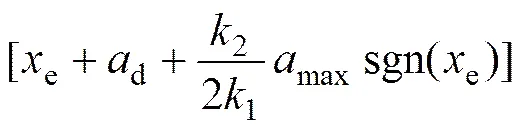
因为1和2均为正值,,且当时,。所以,当时,,即系统渐进稳定。对于深海履带车方向角的系统稳定性可以利用同样的方法得以 证明。
6 路径跟踪仿真
6.1 深海采矿预定路径
对于深海采矿领域,目前国际上普遍提出的深海采集路径为“S”型路径。为了保证履带车海底作业过程安全、高效与环保,韩庆珏等[14]提出了2种新的采集路径,如图3所示。
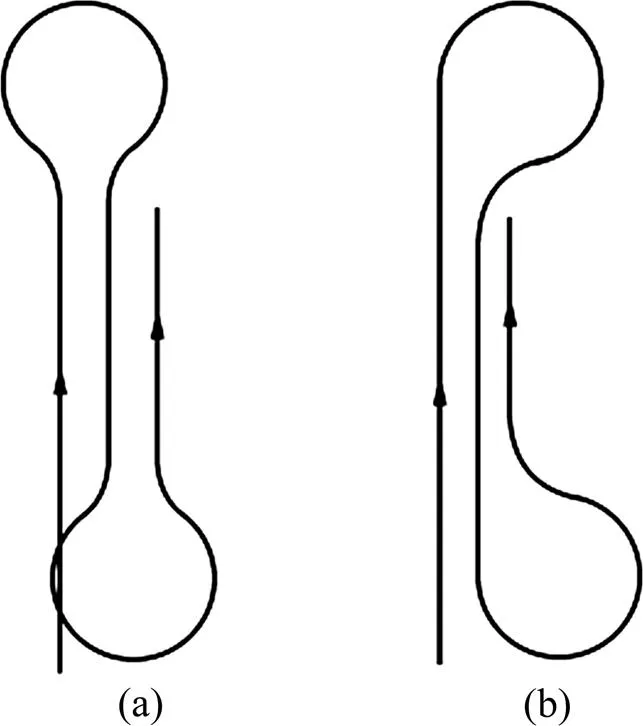
(a) 路径a;(b) 路径b
此2种采集路径(a和b)描述如下。采集路径a示意图见图4。图4中=21.8 m。履带车按采集路径a行走时,需要进行4次调速,如图4中曲线①~④所示。第1次调速使履带车由直线行驶转变为弧线行驶。履带车转向行驶角度=55.97°后进行第2次调速,在转向行驶角度=291.94°时进行第3次调速。再进行转向行驶角度=55.97°后进行第4次调速,最终沿直线行驶。履带车经过此4次调速后,保证2条直线行驶轨迹间距等于履带车的宽度 5.2 m。采集路径b见图5。
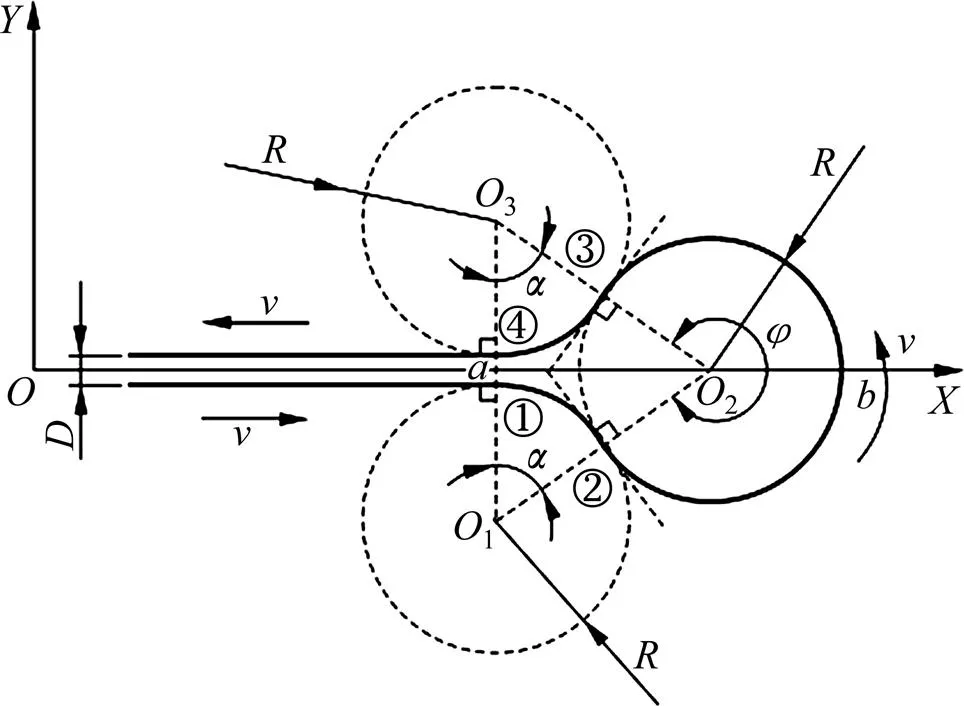
图4 采集路径a示意图
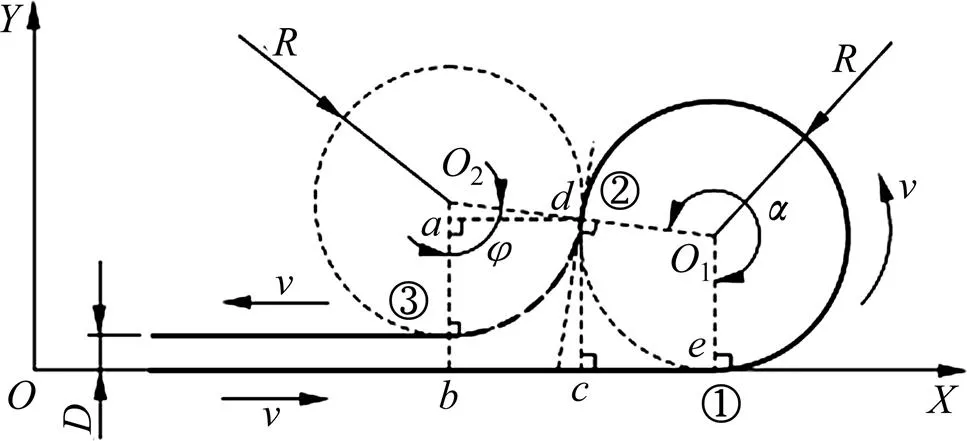
图5 采集路径b示意图
对于采集路径b,履带车经历3次调速,其中,2次转向行驶角分别为=83.15°,=263.15°,圆弧轨迹半径=21.8 m,2条直线轨迹间距=5.2 m。
6.2 仿真分析
为了验证本文所提出的路径跟踪算法的有效性,分别对2种采集路径进行仿真,仿真参数如表1所示。
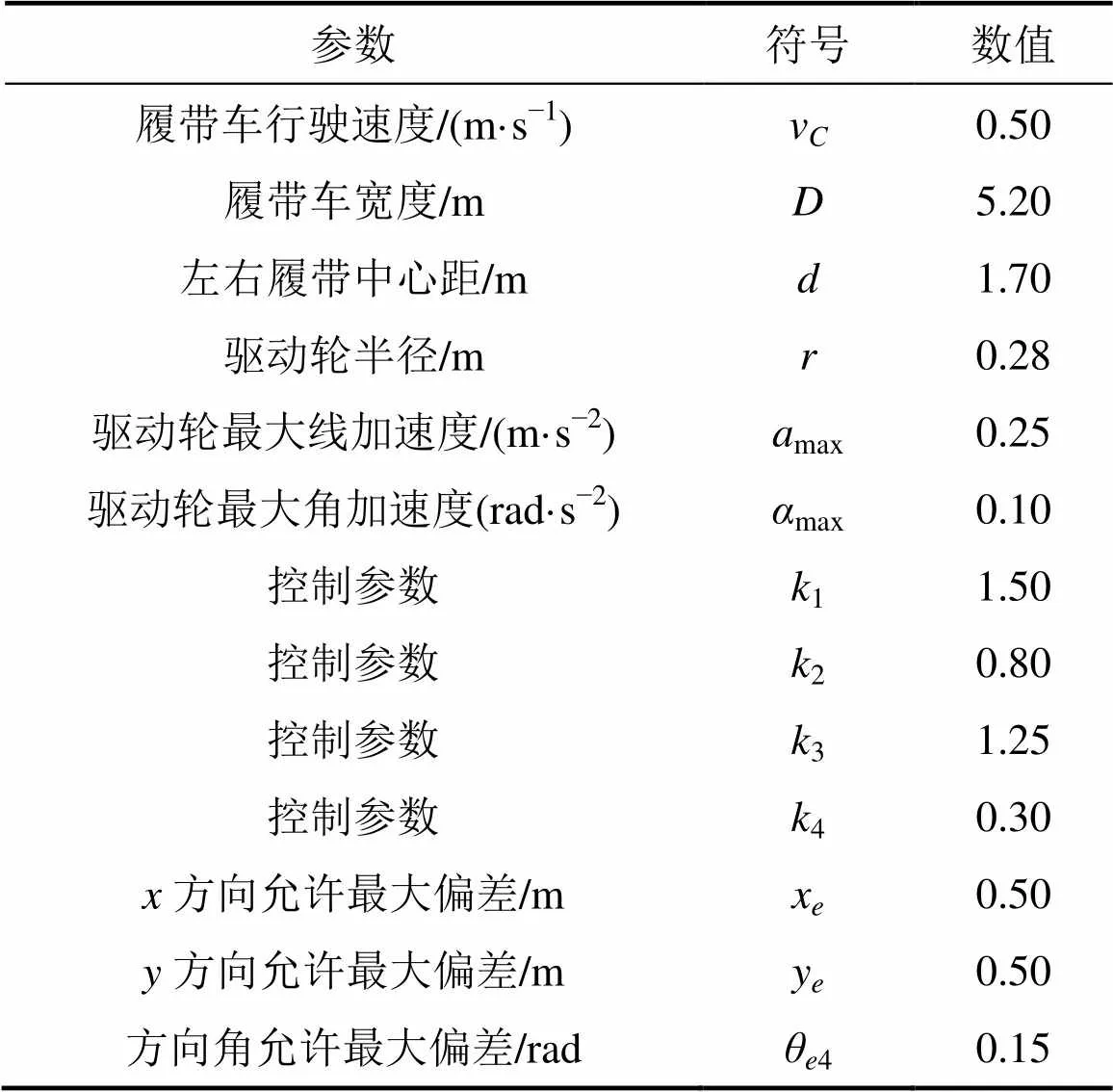
表1 仿真环境参数
2种采集路径的起始位置为(0−0−0)。为了使仿真更具一般性,跟踪采集路径a的仿真中,设定履带车的初始位置为(0,−5,0),属于小偏差路径跟踪;而跟踪采集路径b的仿真中,初始位置偏差设定为(−10,−10,0),属于大偏差路径跟踪。
图6(a)所示为履带车实际行走路线与预定路线仿真对比图。从图6(a)可以看出:仿真开始时履带车初始位置偏差为5 m;履带车自启动后,逐渐朝预定路径方向和位置靠近,水平方向约行走10 m后行驶在期望路径上,此后履带车实际行走路径始终与预定路径吻合,说明路径跟踪效果良好。
图6(b)~(d)所示分别为路径跟踪过程中履带车横向、纵向以及方向角偏差曲线。从图6(b)可以看出:履带车启动时横向位置偏差为0,随后偏差出现波动,这是履带车跟踪过程中不断调整行走速度所致;10 s后横向位置偏差稳定在0处,说明控制算法在横向位置具有良好的快速性和稳定性。
图6(c)所示为纵向偏差曲线。从图6(c)可以看出:履带车启动时纵向偏差为5 m,随后偏差迅速减小;经过10 s左右,纵向偏差稳定在0处,说明此时履带车已沿预定路径行走;但在200~265 s以及480~510 s期间,纵向偏差存在一定波动,波动范围为±0.2 m。这是由于此时履带车处于转弯调速阶段,速度的改变导致跟踪误差再次出现。由于偏差波动范围较小,在误差允许范围内,故可以接受。
图6(d)所示为方向角偏差曲线,其变化规律与纵向偏差一致。同样在200~265 s以及480~510 s期间,由于履带车转弯调速,方向角偏差出现波动,波动范围为±0.1 rad,在误差允许范围内,可以接受。
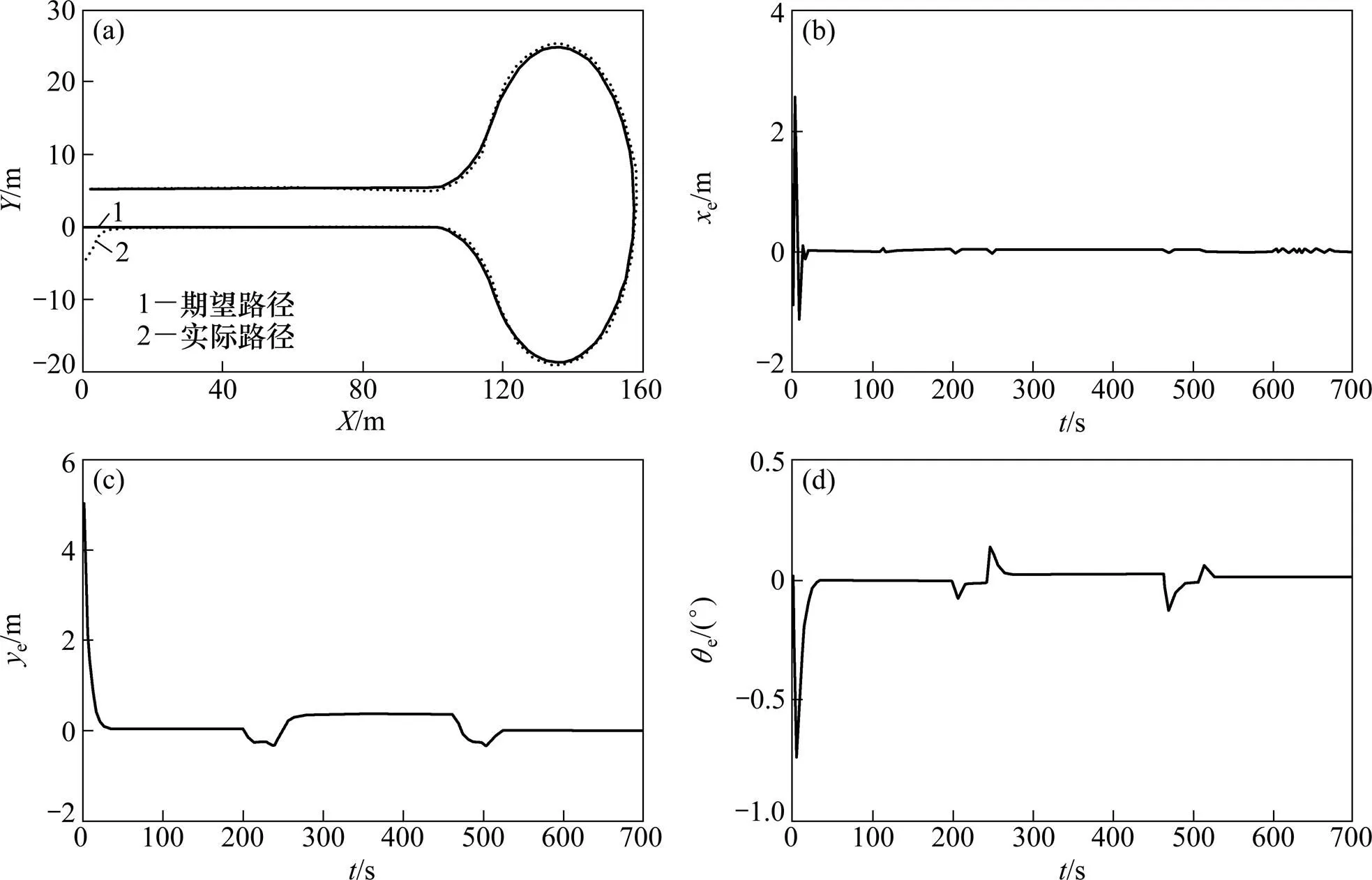
(a) 履带车跟踪预定路径仿真图;(b) 横向偏差曲线;(c) 纵向偏差曲线; (d) 方向角偏差曲线
综合以上对路径跟踪过程横向、纵向以及方向角偏差的分析可知:在采集路径a情况下,所提出的控制策略可以满足履带车路径跟踪要求,控制算法具有良好稳定性。
图7(a)所示为履带车实际行走路线与预定路线仿真对比图。从图7(a)可以看出:仿真开始时履带车初始位置横向、纵向偏差均为10 m,属于大偏差范围;履带车自启动后,迅速朝预定路径方向和位置靠近,水平方向约行走25 m后行驶在期望路径上,此后履带车实际行走路径始终与预定路径吻合,说明路径跟踪效果良好。
图7(b)~(d)所示为路径跟踪过程中履带车横向、纵向以及方向角偏差曲线。从图7(b)可以看出:履带车启动时横向位置偏差为10 m,随后偏差迅速减小;约经过10 s后,偏差减小并稳定在0处。
图7(c)所示为纵向偏差曲线。图7(c)可以看出:履带车启动时纵向偏差为10 m,随后偏差迅速减小并出现一定波动。其原因是在大偏差情况下为保证路径跟踪的快速性,履带车调速。偏差经过15 s后减小并稳定在0处。
图7(d)所示为方向角偏差曲线。从图7(d)可见:其初始偏差为0°,随后突然增大后迅速减小,大约在15 s附近减小并稳定在0°处。这说明履带车启动时与预定路径方向一致。随着路径跟踪过程履带车转弯,导致方向角偏差增大。同时方向角偏差在200~400 s,偏差为0.1 rad;在400~460 s,偏差为−0.1 rad。这说明在采集路径(b)的转弯过程,履带车方向角偏差存在一定误差,由于误差属可接受范围,故整体方向角偏差控制效果良好。
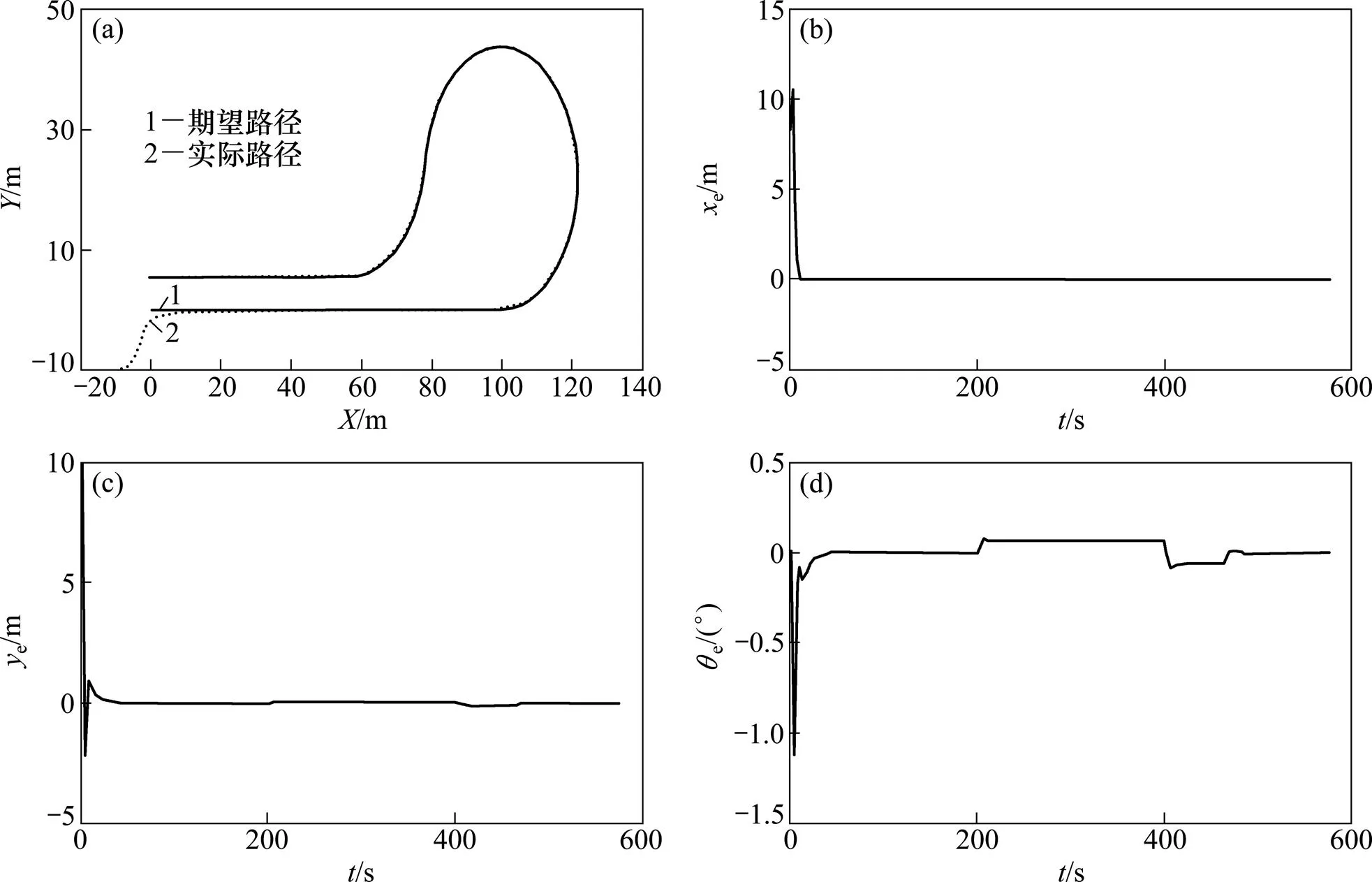
(a) 履带车跟踪预定路径仿真图;(b) 横向偏差曲线;(c) 纵向偏差曲线;(d) 方向角偏差曲线
综合以上对采集路径b时路径跟踪过程横向、纵向以及方向角偏差的分析可知:所提出的控制策略可以满足履带车路径跟踪要求,控制算法具有良好稳 定性。
综合以上仿真结果可知:对于深海采矿不同期望采集路径,本文所提出的路径跟踪算法能使履带车快速有效地跟踪期望采集路径,跟踪过程虽有波动,但仍在可接受范围内。故算法能够满足深海采矿履带车的行走控制要求,保证了履带车良好的行走性能。
7 结论
1) 建立了完整的深海履带车运动学模型和路径偏差模型,并提出了履带车动力约束条件,为深海履带车路径跟踪提供了依据。
2) 基于深海履带车动力约束条件,提出一种新的路径跟踪控制算法,算法中引入速度中间变量,保证了系统的动力要求。运用李雅普诺夫方法证明了算法的稳定性。
3) 针对深海采矿2种不同期望采集路径,对路径跟踪控制进行仿真,仿真结果满足路径跟踪控制要求,保证了深海履带车行走的准确性。
下一步将着重于路径跟踪控制实验研究。
[1] 戴瑜. 履带式集矿机海底行走的单刚体建模研究与仿真分析[D]. 长沙: 中南大学机电工程学院, 2010: 1−10.
DAI Yu. The modeling research and simulation analysis on the single-rigid-body of tracked miner moving on the seafloor[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2010: 1−10.
[2] Herber G, Kostas J. Discontinuous backstepping for stabilization of nonholonomic mobile robots[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Washington DC, 2002: 3948−3953.
[3] Endo D, Okada Y, Keiji N, et al. Path following control for tracked vehicles based on slip-compensation odometry[C]// Proceedings of the International Conference on Intelligent Robots and Systems. San Diego, USA, 2007: 2871−2876.
[4] Keiji N, Endo D, Yoshida K. Improvement of the odometry accuracy of a crawler vehicle with consideration of slippage[C]//Proceedings of International Conference on Robotics and Automation. Roma, Italy, 2007: 2752−2757.
[5] ZHOU Bo, HAN Jianda. Nonlinear estimation methods for autonomous tracked vehicle with slip[J]. Chinese Journal of Mechanical Engineering, 2007, 20(4): 1−7.
[6] 徐俊艳, 张培仁. 非完整轮式移动机器人轨迹跟踪控制研究[J]. 中国科学技术大学学报, 2004, 34(3): 376−380.
XU Junyan, ZHANG Peiren. Research on trajectory tracking control of nonholonomic wheeled mobile robots[J]. Journal of University of Science and Technology of China, 2004, 34(3): 376−380.
[7] Schulte E, Handschuh R, Schwarz W. Transferability of soil mechanical parameters to traction potential calculation of a tracked vehicle[C]//International Society of Offshore and Polar Engineers. Proceedings of the 5th ISOPE Ocean Mining Symposium. Tsukuba, Japan: ISOPE, 2003: 123−131.
[8] Yeu T K, Hong S, Kim H W. Path tracking control of tracked vehicle on soft cohesive soil[C]//Proceedings of the Sixth ISOPE Ocean Mining Symposium. Changsha, China, 2005: 168−173.
[9] Yeu T K, Park S J, Hong S. Path tracking using vector pursuit algorithm for tracked vehicles driving on the soft cohesive soil[C]//Proceedings of SICE-ICASE International Joint Conference. Busan, Korea, 2006: 2781−2786.
[10] Hong S, Choi J S, Kim H Y, et al. A path tracking control algorithm for underwater mining vehicles[J]. Journal of Mechanical Science and Technology, 2009, 23(8): 2030−2037.
[11] WANG Suiping, GUI Weihua, ZHANG Tao, et al. Fuzzy and predictive control on the deep-sea vehicle[C]//Proceedings of the Sixth ISOPE Ocean Mining Symposium. Changsha, China, 2005: 181−186.
[12] 李力, 邹兴龙. 海底机器人自动跟踪预定开采路径[J]. 机械工程学报, 2007, 43(1): 152−157.
LI Li, ZOU Xinglong. Seafloor robots control on tracking automatically planning mining paths[J]. Chinese Journal of Mechanical Engineering, 2007, 43(1): 152−157.
[13] DAI Yu, LIU Shaojun. Theoretical design and dynamic simulation of new mining paths of tracked miner on deep seafloor[J]. Journal of Central South University, 2013, 20(4): 918−923.
[14] 韩庆珏, 刘少军, 戴瑜, 等. 水下履带式采矿车作业环境下的动力学分析及路径跟踪控制[J]. 中南大学学报(自然科学版), 2011, 42(2): 307−312.
HAN Qingjue, LIU Shaojun, DAI Yu. Dynamic analysis and path tracking control of tracked underwater miner in working condition[J]. Journal of Central South University (Science and Technology), 2011, 42(2): 307−312.
Path tracking control algorithm of the deep sea tracked vehicle
HAN Qingjue, LIU Shaojun
(National Key Laboratory of Development and Utilization of Deep-Sea Mineral Resource,School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
The kinematic and position error model of the deep sea tracked vehicle was established, and a new path tracking control algorithm was proposed to solve the path error problem of tracked vehicle during working. Based on the dynamic constraints, two intermediate variables were introduced in the control algorithm to avoid the systematic instability due to abrupt change in angular velocity of the vehicle sprocket. To improve the response time of the system, a proportional element was introduced in the algorithm. Meanwhile, the stability of the control system was proved using Lyapunov method, and a series of simulations of tracking two typical deep sea mining desired paths were carried out. The results show that the suggested algorithm is valid and can meet the control requirement; therefore, the walking performance of the tracked vehicle is ensured.
deep sea; tracked vehicle; path tracking; algorithm
TP242
A
1672−7207(2015)02−0472−07
2014−03−10;
2014−05−21
国家自然科学基金资助项目(51074179);国家高技术研究发展计划(863计划)项目(2012AA091201)(Project (51074179) supported by the National Natural Science Foundation of China; Project (2012AA091201) supported by National High Technology Research and Development Program of China (863 Program))
韩庆珏,博士研究生,从事海底履带采矿车行走控制研究;E-mail:qingjuehan@yahoo.com.cn
10.11817/j.issn.1672-7207.2015.02.014
(编辑 陈灿华)
