基于冒泡原理的模块化多电平换流器快速电压均衡控制策略

喻 锋，王西田

（上海交通大学 电气工程系 电力传输与功率变换控制教育部重点实验室，上海 200240）

0 引言

模块化多电平换流器MMC（Modular Multilevel Converter）作为一种新型电压源换流器结构，采用子模块SM（Sub-Module）级联型拓扑，具有模块化结构易于扩展、低次谐波含量低、损耗小的优点[1-3]，在HVDC方向得到大力推广。

作为MMC关键技术之一的电压均衡控制，其研究的目的是为了在保证各悬浮电容器电压的均衡前提下减小开关的动作频率。鉴于电压均衡控制对于MMC稳定运行的重要作用，国内外学者在均衡控制算法方向进行了大量的研究。文献[4]提出了为子模块电容电压设计闭环控制，但复杂的控制系统使其局限于较低电平的应用。文献[5]提出了基于能量平均的电压均衡控制策略，该算法不需测量电容电压，减少了硬件的投入，但该算法计算复杂且其暂态稳定性有待进一步验证。而对于大多数均衡控制策略采用了基于电容电压排序算法，该类算法原理清晰，实现简单，为多数文献所采用[6-14]。文献[6]引入保持因子，使电容电压具有保持原来开关状态的能力，降低了开关器件的动作频率。文献[7-8]对传统直接由电压排序和桥臂电流方向确定子模块触发脉冲的方法进行了改进，引入子模块间最大电压偏差量控制，降低了排序的频率，一定程度上减少了IGBT不必要的开断操作。

随着MMC-HVDC传输容量及直流电压等级的提升，受电力设备耐压的限制，桥臂串联的子模块需要相应的增加[9]。 TRANS BAY CABLE Project是世界上第一个使用MMC技术的柔性直流输电工程，其额定容量为400 MW，单个桥臂串联子模块已达到200个[10]。当MMC电平数增长达到数百时，电压均衡控制策略的排序运算占用的计算资源将不能忽视。文献[11]对基于排序的电压均衡控制算法的运算量及时间复杂度进行了分析，通过双保持因子降低子模块的开关动作的频率，采用分组排序减小排序运算量。但分组排序及组间能量的均衡增加了控制策略的复杂度。

为了减少直流电容电压排序耗费控制系统的计算资源，提高控制系统的响应速度，本文设计了一种快速的电容电压均衡控制策略，相比传统排序极大地减小了电压均衡控制策略的计算量。该策略利用冒泡原理简化了电容电压的排序过程，通过参数的设置能够在较低开关频率下实现电压的均衡控制。最后通过PSCAD/EMTDC时域仿真模型对本文所提出的均衡控制策略的有效性进行了验证。

1 MMC基本原理

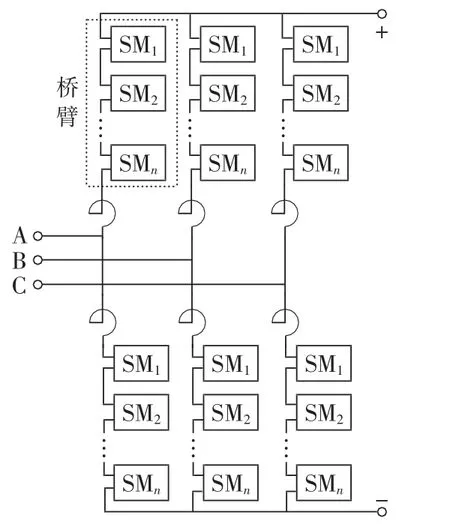
图1 MMC拓扑结构图Fig.1 Topology of MMC

MMC拓扑结构如图1所示，换流器由3个相单元组成，每相各有上、下2个桥臂，每个桥臂串联n个子模块。半H桥型子模块结构HBSM（Half-Bridge SM）如图2所示，其中IRM为桥臂电流，UC为电容电压。每个子模块共有2个IGBT开关及反并联二极管，在正常运行状态下，当VT1导通时，USM等于直流电容电压UC；当VT2导通时，USM等于0。假设直流电容额定电压为UCref，保持上、下桥臂同时投入的子模块总和为n，可以维持直流电压Udc恒定，通过控制上、下桥臂投入子模块个数可以使各相跟踪控制系统调制电压[15]。

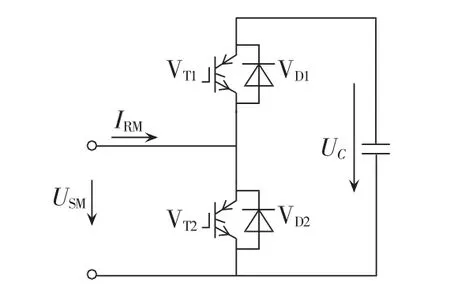
图2 SM结构图Fig.2 Structure of SM

2 脉冲调制技术

目前常用的MMC调制方法可以划分为两大类：脉宽调制（PWM）技术[16]和阶梯波调制（staircase modulation）技术[12]。 当电平数较低时，采用 PWM 技术能够明显改善低电平换流器的输出特性，但随着电平数的增加，过于复杂的控制系统及因高频调制方式导致的过大的损耗使该种技术不再适用。最近电平控制 NLC（Nearest Level Control）[13]技术作为阶梯波调制技术的一种，其原理为使用最接近的电压电平瞬时逼近调制波。NLC实现简单，当电平数足够多时能够在较低开关频率下跟踪调制电压，尤其适合于大功率应用场合，其具有开关频率低、损耗小的优点。NLC调制技术原理如图3所示，随着正弦调制波升高，下桥臂将投入的子模块逐步增加，而上桥臂将投入的子模块相应地减少，使相单元的输出电压随着正弦调制波而变化。

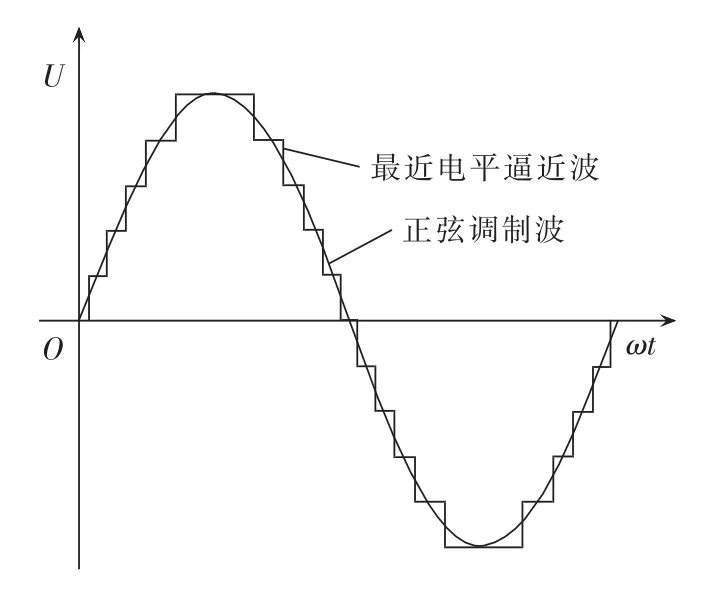
图3 NLC原理图Fig.3 Schematic diagram of NLC

3 基于冒泡原理的均衡控制策略

3.1 冒泡原理

冒泡（Bubble）是计算机科学领域的一种简单算法。它的原理为访问要排序的数列，一次比较数列中相邻储存的2个元素，按照元素大小对其位置进行调整。下面以降序冒泡为例，对算法的流程说明如下：从数组的最后一个元素开始，比较相邻的2个元素，如果当前单元的元素值大于上一单元的元素值，则交换两者位置，否则保持元素现有位置不变，从后向前直到比较到数组第一个元素为止。这样的一次降序冒泡运算可以将数组中最大的元素移至数组的前列，同理升序冒泡可以将数组最小的元素移至数组的前列。而对于m次冒泡运算则可将m个较大元素移动到数组中指定的位置。

3.2 基于冒泡原理的均衡控制策略

对于级联结构的MMC，如何保证各子模块悬浮电容器的电压均衡是MMC控制系统设计需要考虑的主要问题之一。当MMC应用于高压应用领域时需采用较低开关频率的NLC，而适用于该调制技术的电压均衡控制大多需要对电容电压排序。排序运算占用了大量的控制系统计算资源，加重了控制器的负担。文献[6-7]对传统的电压均衡控制方法进行改进，通过分别对投入和退出状态的子模块排序来完成最值寻找，并根据电流方向及投入电平数变化来改变最值电容器的运行状态，维持桥臂整体的电压均衡。该类方法虽然将电压排序限定在了2个分块内，相比对桥臂内所有子模块排序的算法，一定程度上降低了计算量，但减小的幅度有限。

对于投入子模块数变化量为ndiff的控制，其需要改变运行状态的对象是最值子模块，因此只需计算得出投入或者退出子模块中ndiff个最值子模块即可。如果采用冒泡比较ndiff次运算就可达到要求，相比于全排序，极大地减小了运算量。对于采用NLC的MMC系统，为了降低系统谐波含量，需要提高控制器的控制频率，使MMC中的各子模块得到充分利用[14]。此时投入电平将以较小的幅度变化，如图3所示。如果每个控制周期内对投入状态和退出状态的子模块分别冒泡寻找最值，则仅需较少次运算即可完成。为此本文在利用冒泡原理的基础上设计了一种无需对电容电压进行排序的快速均衡控制策略。该策略实现过程如图4所示。各种工况下电压均衡控制的具体方法详述如下。

a.创建子模块序号记录向量Von及Voff，分别记录投入子模块序号及退出子模块序号，设定投入与退出子模块间允许最大电压偏差ΔU。对序号记录向量Von及Voff加以保存，前一仿真周期Von及Voff最后计算值将作为下一周期Von及Voff计算的初始值。

图4 电压均衡控制策略流程图Fig.4 Flowchart of voltage balancing control

b.本文定义冒泡规则如下：当桥臂电流大于零时，对Von记录的子模块序号按电容电压从尾部开始进行降序冒泡，即将投入状态电压值最高的子模块序号移至Von的头部；对Voff记录的子模块按电容电压从尾部开始进行升序冒泡，即将退出状态电压值最小的子模块序号移至Voff的头部。当桥臂电流小于零时，对Von记录的子模块按电容电压从尾部开始进行升序冒泡，即将投入状态电压值最小的子模块序号移至Von的头部；对Voff记录的子模块按电容电压从尾部开始进行降序冒泡，即将退出状态电压值最高的子模块序号移至Voff的头部。

c.接收上一控制周期计算得到的序号记录向量Von、Voff及当前投入子模块数 non。

d.由电平调制策略计算需要投入子模块数nref，则投入子模块数变化量ndiff=nref-non。当ndiff=0，即投入电平数不变时保持现有的Von及Voff不变。当时，对投入和退出子模块组进行次冒泡运算（为绝对值运算符）。当ndiff＜0时，即要退出部分已投入的子模块，将冒泡运算后Von中记录的前个子模块序号逆序移至Voff的尾部，Von依次上移。当ndiff＞0时，即要投入更多的子模块，将Voff中记录的前ndiff个子模块序号逆序移至Von的尾部，Voff依次上移。当ndiff＞0时的调整示意图如图5所示，其中i′表示Von中位置i储存的子模块序号；相应的i″表示Voff中位置i储存的子模块序号。由步骤b可知，不论桥臂电流大于0或者小于0，冒泡操作均是将需要改变状态的子模块移至序号记录向量的前列，因此投入子模块数调整时无需再次对桥臂电流进行讨论。

e.电压偏差控制。为了保持投入子模块组与退出子模块组电压的相对一致，维持整体电压稳定性，需要对两者之间的最大电压偏差进行控制。

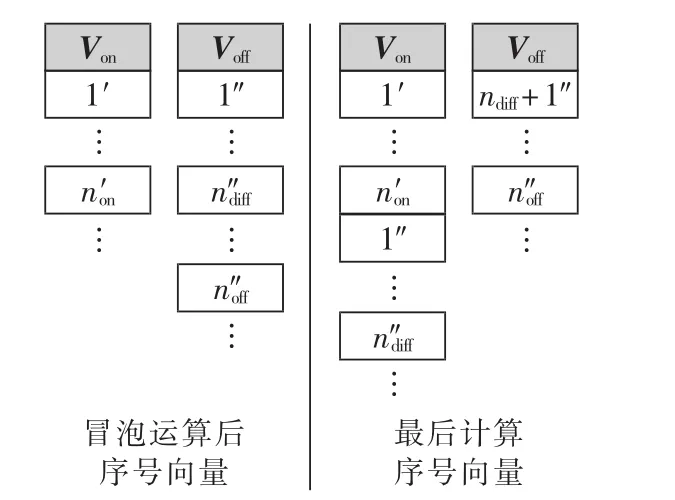
图5 投入子模块数变化时均衡控制示意图Fig.5 Schematic diagram of balancing control when number of on-state sub-module changes

当桥臂电流大于零时，首先进行一次冒泡运算，若Von（1）对应的投入子模块最大电容电压值大于Voff（1）对应的退出状态子模块组最小电压值与ΔU的和，则表示组间电压偏差过大，继续冒泡、比较。直到投入子模块组中元素Von（m+1）对应的电容电压小于退出模块中元素Voff（m+1）对应的电容电压与ΔU的和。将Von的前m个元素逆序存入Voff的尾部，将Voff中的前m个元素逆序存入Von的尾部，将Von及Voff中其他元素依次上移m次。当电流大于0，电压偏差调整示意图如图6所示。

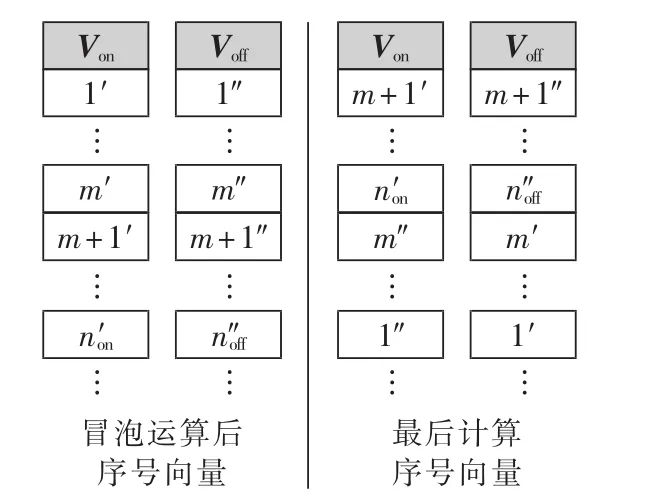
图6 电压偏差控制示意图Fig.6 Schematic diagram of voltage deviation control

当桥臂电流小于零，首先进行一次冒泡运算，若Von（1）对应的投入子模块最小电容电压值与ΔU的和小于Voff（1）对应的退出状态子模块组最大电压值，则表示组间电压偏差过大，继续冒泡、比较。直到投入子模块组中元素Von（m+1）对应的电容电压与ΔU的和大于退出模块中元素Voff（m+1）对应的电容电压与ΔU的和。将Von的前m个元素逆序存入Voff的尾部，将Voff中的前m个元素逆序存入Von的尾部，将Von及Voff中元素依次上移m次。

f.Von中记录序号的子模块设置为投入状态；Voff中记录序号的子模块设置为退出状态。保存本控制周期的Von、Voff及nref为下一控制周期使用。

本文提出的电压均衡控制策略对上一步投入和退出子模块序号进行了保存，每一步电压偏差控制都会额外进行一次冒泡，使保存的子模块序号趋于有序化。同时通过保证基本次数的冒泡运算保证了算法的有效性。投入子模块与退出子模块间交换能够保证不同状态的子模块间电容电压在可控的范围内，同时电压偏差参数控制能够限制因为微小的电压差值而造成的开关的频繁动作。

4 仿真验证

在PSCAD/EMTDC仿真平台上搭建了21电平MMC-HVDC输电系统，如图7所示，对本文提出的基于冒泡原理的快速电压均衡控制策略的有效性进行验证。其中交流系统额定电压均为220 kV，直流线路电压为±200 kV，传送容量为600 MW。子模块电容值为3000 μF，环流电抗器电感值为0.04 H。采用了文献[17]提出的技术对环流进行抑制。

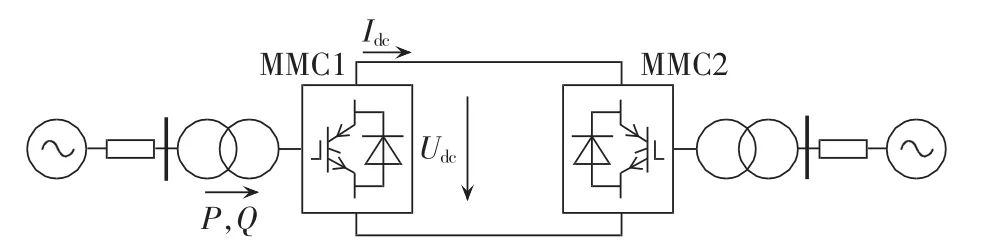
图7 MMC-HVDC系统结构图Fig.7 Structure of MMC-HVDC system

若nsw为桥臂内所有子模块的开关次数，则其平均开关频率 fsw可以表示为[18]：

图8为不同ΔU参数条件下桥臂电容电压及触发脉冲仿真计算结果。由图可知，随着最大电压偏差控制参数的增大，子模块平均开关频率下降，当ΔU=1 kV、电压允许波动值为额定值的5%时，fsw已经下降到了100 Hz以下。虽然在参数增大的过程中，电容电压的一致性减弱，但其仍在可控的范围内。

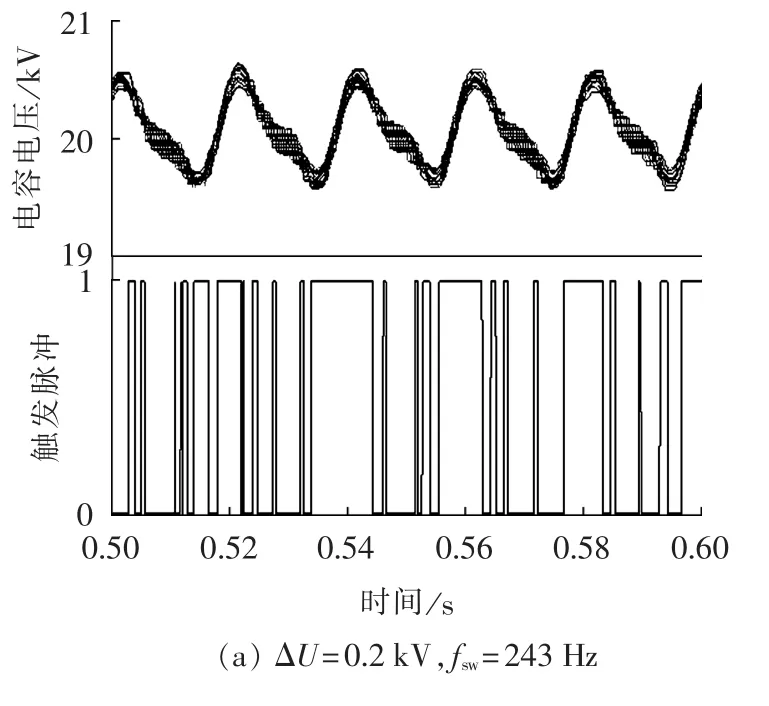
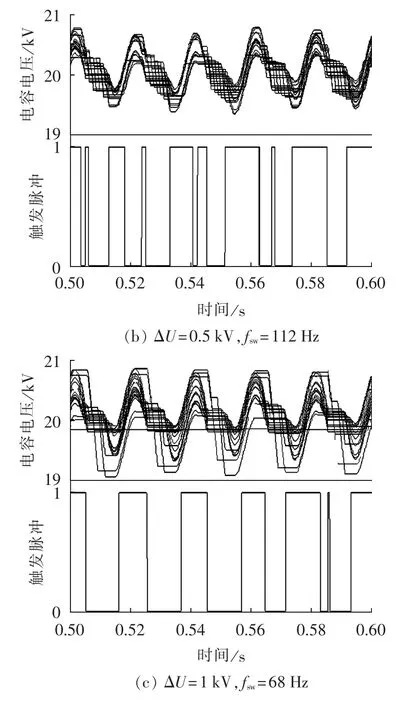
图8 算例仿真结果Fig.8 Simulative results of cases

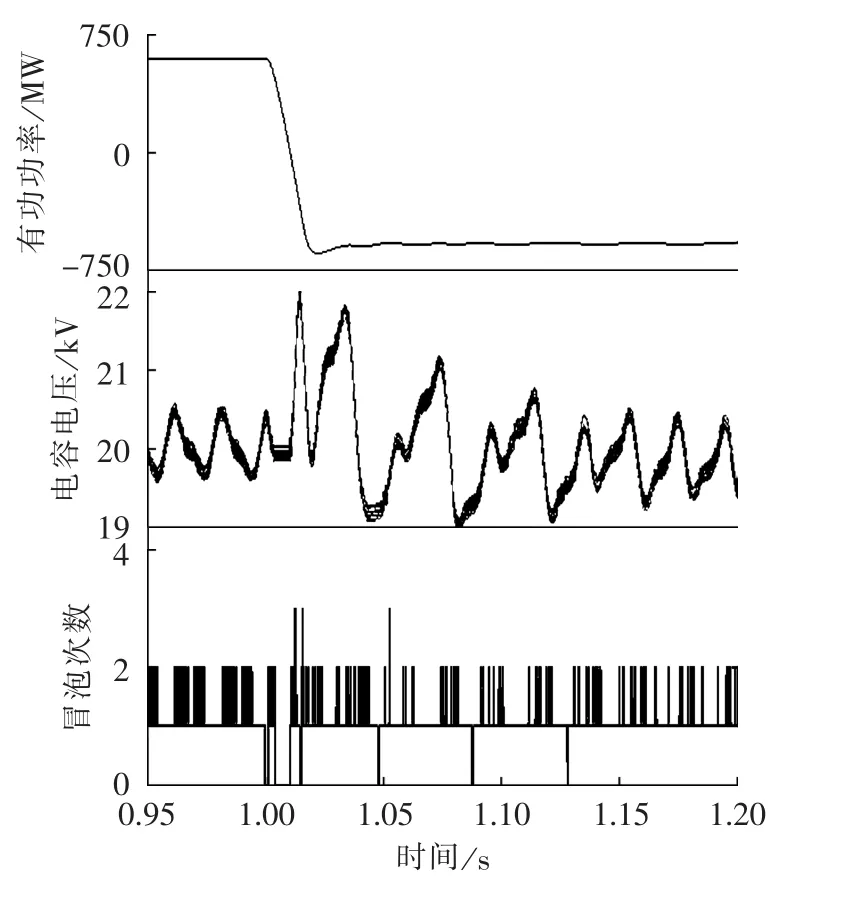
图9 有功功率翻转仿真结果Fig.9 Simulative results of active power reversal

图9为模拟MMC1侧功率发生翻转的过程中各特征量仿真计算结果，其中1 s时MMC1侧传送功率由600 MW改变为-600 MW。由图9可以看出，在传输有功功率发生大幅度变化的暂态过程中，本文提出的均衡控制算法也能完成电压均衡控制的任务，且在功率调整的过程中冒泡次数也保持在较低水平，进一步表明本文提出的算法在电力系统大扰动条件下也是有效的。

为了验证本文提出的电压均衡控制策略对计算量的优化效果，在PSCAD/EMTDC上分别搭建了21、101及201电平的MMC模型[19-20]，并对提出的均衡控制策略在每个周期内平均冒泡的次数进行统计。系统均运行于额定工况下，电压允许波动值均为额定值的5%，仿真步长为20 μs。由于换位操作具有不可预测性，且其最大值不大于比较运算的次数，因此可以通过比较运算次数来确定各均衡算法的效率。对于桥臂子模块总数为n的MMC，每次冒泡计算量为n-1，基于排序算法（包括全排序及投入、退出分块排序）的计算量为。 则本文提出的均衡控制算法的计算量与采用传统排序算法计算量对比如表1所示。由表1可得，每个周期内，本文提出的均衡控制策略相比于传统排序计算量减少明显；而且随着电平数的增加，本文提出的均衡控制策略的优化效果更加显著。

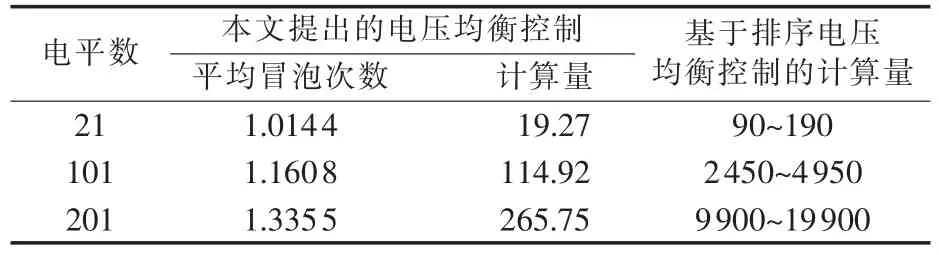
表1 计算量对比Table 1 Comparison of calculation load

5 结语

本文提出了一种基于冒泡原理的MMC快速电压均衡控制策略，该策略改变了传统电压均衡控制策略需对电容电压进行排序的常规思路，以用较少计算量来完成电容电压均衡控制为目的。该策略结合NLC调制技术的特点，以冒泡运算寻找投入或者退出状态子模块电容电压的最值，改变最值子模块的运行状态以满足维持电压均衡的要求。设置了组间允许最大电压偏差允许组间子模块交换，维持了桥臂整体电压稳定性，并一定程度上可以控制开关动作频率。

在PSCAD/EMTDC仿真计算平台上搭建了MMC-HVDC模型，对本文提出的快速电压均衡控制策略的有效性进行验证，结果表明本文设计的控制策略可以在较少计算量的前提下实现电压的均衡控制。