基于伪谱法的电力系统暂态稳定紧急控制
2015-09-21冯军基耿光超江全元
冯军基,耿光超,王 云,江全元
(浙江大学 电气工程学院,浙江 杭州 310027)
0 引言
随着电力市场化改革的深入和电网规模的扩大,电力系统在遭受大扰动或突发故障下的安全稳定问题日益突出[1]。为保证电力系统在故障切除后仍能稳定运行,需要及时对系统进行紧急控制,切机、切负荷是应用最广的2种措施。
暂态稳定约束紧急控制TSCEC(Transient Stability Constrained Emergency Control)问题的解决方法主要有3类:第一类是基于暂态能量函数的直接法[2-4];第二类是试凑法和启发式算法[5-6];第三类方法将原问题描述为包含微分代数方程组(DAE)约束的最优控制问题OCP(Optimal Control Problem)进行求解[7-9]。
文献[2]采用基于最大势能搜索的势能边界面法(PEBS)计算临界势能,但计算结果存在可靠性问题。文献[3]采用主导不稳定平衡点法(BCU)制定紧急控制策略,有可能因为失稳模式判断错误引起误差,计算结果偏于保守。文献[4]基于扩展等面积法则(EEAC)提出了一种动态安全域方法,但是受等效模型限制,不适用于非线性时变因素较强的大系统。
文献[5]和文献[6]分别使用神经网络算法和蚁群算法进行切机、切负荷计算,启发式算法直观简单,易于获得可行解,但花费的计算时间较多。
文献[7]使用约束转化方法和控制向量参数化方法求解最优控制问题,将TSCEC分解为灵敏度计算和非线性规划(NLP)问题交替求解。文献[8]和文献[9]分别使用隐式梯形积分算法和有限元正交配置 OCFE(Orthogonal Collocation on Finite Elements)算法将暂态稳定约束离散化后,对生成的NLP问题进行求解。
基于最优控制理论的TSCEC求解算法首先对暂态稳定约束进行处理,然后利用非线性优化算法进行迭代计算。OCP的求解策略包括间接法(变分法)和直接法,后者具有较好的收敛性,能方便地处理不等式约束,成为最优控制的主要研究方向[10]。根据对DAE的处理方式,直接法又分为序贯法和联立法。序贯法包括控制向量参数化和多重打靶法;联立法包括隐式梯形积分、有限元正交配置和伪谱法PS(Pseudo-Spectral method)等方法。近年来,伪谱法作为一种高阶方法,得到了迅速的发展,并在航天、化工等领域广泛应用[11-14]。
在使用低阶的隐式梯形积分等联立法求解TSCEC问题时,会由大量的离散点生成高维系统,导致计算困难。本文将高阶的伪谱法引入TSCEC问题,以伪谱法配置离散点,采用内点法进行求解,并在不同规模系统上与有限元正交配置方法进行对比,该方法具有以下特点:数值解收敛半径大,对初值猜测不敏感,鲁棒性强;计算精度高,可以用较少的离散点数量获得较精确的解,降低NLP系统规模;通过细粒度并行可以大幅提高计算性能。
1 暂态稳定紧急控制问题的建模
暂态稳定约束的紧急控制问题可以描述成一个DAE约束的最优控制问题:以切机与切负荷量最小为目标,使系统运行满足暂态稳定约束。
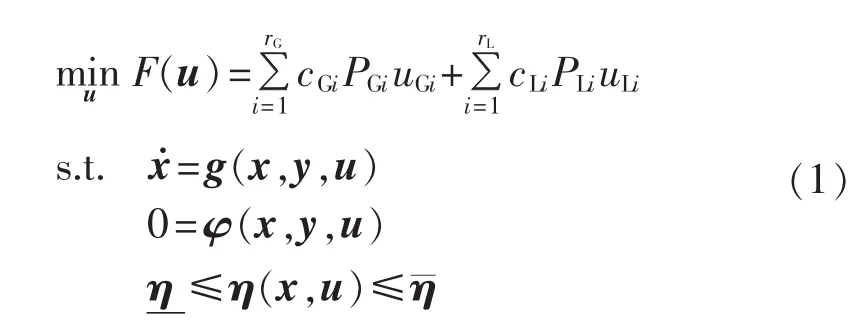
其中,u=[uG,uL]为切机、切负荷比例的控制向量,其为非时变量;cG、cL与PG、PL分别为可切负荷与可切发电机节点的权值与功率向量,cGi、cLi、PGi、PLi分别为对应向量的第i个元素;x为系统的状态变量,y为系统的代数变量,x、y均为时变量。
1.1 等式约束
TSCEC的等式约束是一组DAE方程组。微分方程组 x˙=g(x,y,u)包含发电机转子运动方程、励磁系统与调整系统动态方程;代数方程组 0=φ(x,y,u)主要为电力网络方程。
第i台发电机的转子运动方程可以描述为:
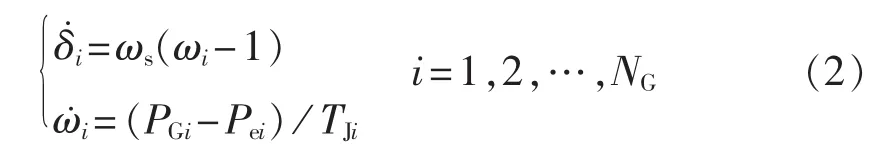
其中,NG为发电机数目;δi为发电机功角;ωi为发电机角速度;PGi为发电机有功功率;Pei为发电机电磁功率;TJi为发电机惯性时间常数。
电力网络方程YU=I可写为:
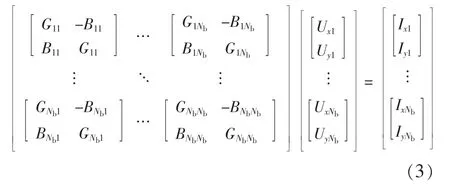
其中,Y为节点导纳矩阵;Yij=Gij+jBij为节点i和j的互导纳;Yii=Gii+jBii为节点 i的自导纳;Uxi、Uyi分别为节点i电压的实部、虚部;Ixi、Iyi分别为注入电流的实部、虚部,非发电机节点注入电流为0。
对于有可切发电机的节点i,假设发电机等值导纳为YGi=GGi+jBGi,则切除后节点i的自导纳为G′ii=Gii-uGiGGi、B′ii=Bii-uGiBGi,注入电流为 I′xi= (1-uGi)Ixi、I′yi= (1-uGi)Iyi。
对于有可切负荷的节点i,假设负荷等值导纳为YLi=GLi+jBLi,则切除后节点i的自导纳为G′ii=GiiuLiGLi、B′ii=Bii-uLiBLi。
1.2 不等式约束
不等式约束包括暂态稳定约束和控制向量的上下限约束。本文用各发电机功角与惯性中心角的偏差不超过指定角度作为暂态稳定判据。不等式可以用式(4)表示。
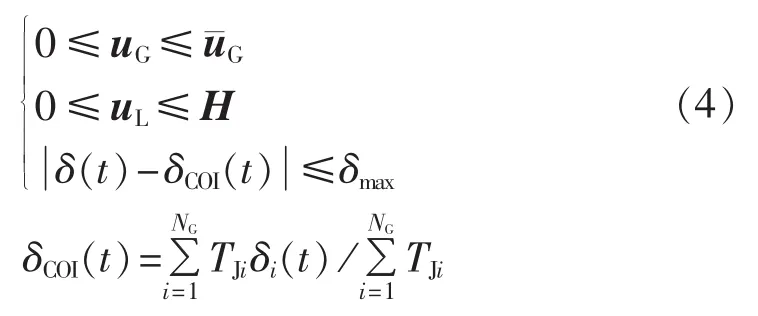
2 伪谱法原理
伪谱法是一种全局正交配置方法,它通过对状态变量和代数变量进行离散,将含有时变变量的约束转化为非时变的代数等式/不等式约束,使含DAE约束的最优控制问题转化为普通的NLP问题。
2.1 全局配置法
全局法在整个问题区间上通过一系列多项式逼近状态变量。伪谱法通常选取三角多项式、勒让德多项式等正交多项式为基函数,在正交配置点上离散变量,用有限序列之和逼近真实解。
假设在优化区间[t0,tf]上配置有 R 个点[t1,t2,…,tR],状态变量 x(t)和代数变量 y(t)在 ti点的离散值分别为 Xi、Yi,为求取 x˙(t)在离散点的数值,将 x(t)用拉格朗日多项式表示如下:
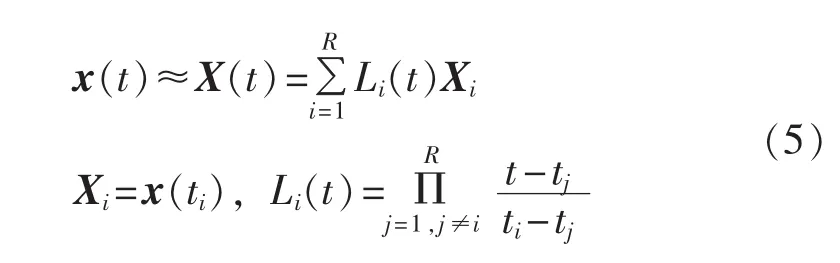
对式(5)进行微分得到:
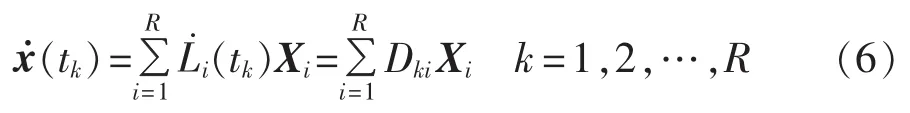
其中,矩阵 D={Dki}为微分矩阵。
2.2 配置点选取
如果用等距的配置点进行多项式插值,一般可以通过配置更多的点提高逼近程度,但在一些情况下,点数增多会导致插值区间边缘产生无穷大误差,称为龙格(Runge)现象[15]。选用正交多项式的根作为配置点是消除龙格现象的一种有效方法。
勒让德正交多项式满足递推关系[16]和正交关系分别如式(7)、(8)所示。
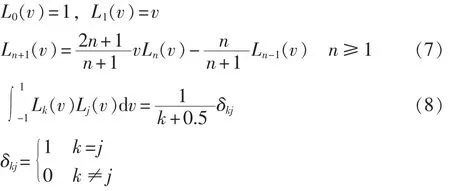
其中,δkj为 Kronecker函数。
常用如下3类配置点。
a.Legendre-Gauss点:选用 LN+1(v)=0 的根 vj(0≤j≤N)。
b.Legendre-Gauss-Radau 点:选用 LN(v)+LN+1(v)=0 的根 vj(0≤j≤N)。
c.Legendre-Gauss-Lobatto 点:v0=-1,vN=1,{vj}N-1j=1为 L′N(v)=0 的根。
在[-1,1]区间上用3类方法进行5节点配置的点分布如图1所示,Legendre-Gauss法不包含优化区间端点,Radau法仅包含1个端点,Lobatto法包含2个端点。

图1 正交配置点分布Fig.1 Distribution of orthogonal collocation points
理论上,Legendre-Gauss-Radau点在处理刚性问题时具有良好的稳定性[17],最优化软件包GPOPS-Ⅱ就以该方法为基础实现离散点配置[14]。本文也选用Radau方法进行最优控制。
3 算法实现
3.1 原问题到NLP的转化
设区间[-1,1]上的 Legendre-Gauss-Radau 配置点为[τ0,τ1,…,τM],其对应的标准化微分矩阵为:
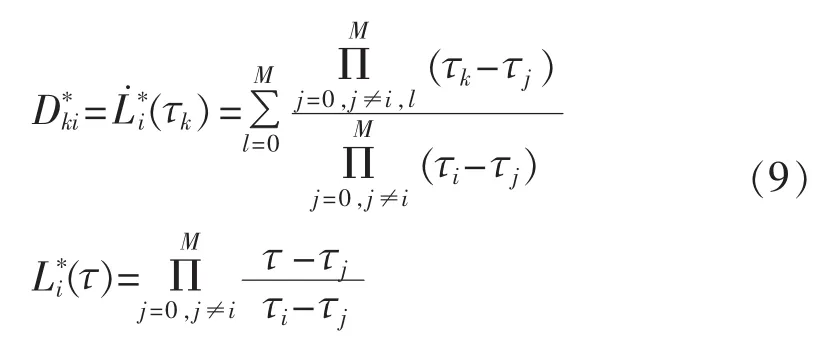
其中,k=0,1,…,M-1;i=0,1,…,M。
将变量τ∈[-1,1]变换到优化区间 t∈[t0,tf]:
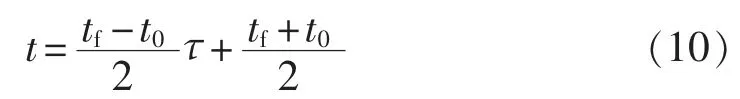
区间[t0,tf]对应的离散点为[t0,t1,…,tN],微分矩阵为:

在 t=tk处等式约束 x˙=g(x,y,u)的离散化形式为:
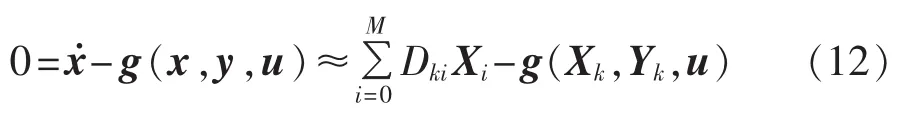
其中,Yk是代数状态变量在t=tk处的值。
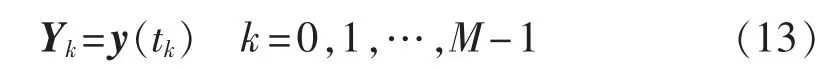
DAE约束的紧急控制问题可以转化为下面的NLP问题:
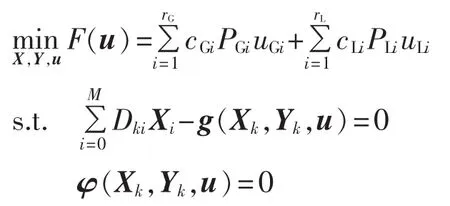
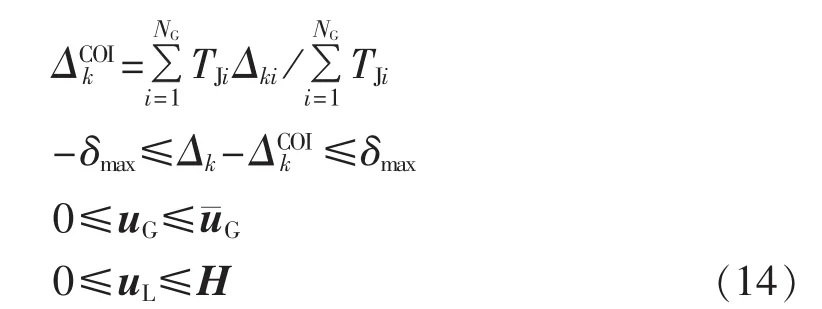
其中,Δk⊂Xk、ΔCOIk⊂Yk(k=0,1,…,M)。 优化变量为Xk、Yk、u=[uG,uL]。
3.2 NLP求解
通过离散生成的NLP问题是一个不含微分方程的大规模稀疏问题。常用的NLP求解算法有序列二次规划 SQP(Sequential Quadratic Programming)法、内点法 IPM(Interior Point Method)等。
在求解时,需要提供初始点、雅可比矩阵和海森矩阵信息。
a.初始点:在控制时刻前进行暂态仿真,选取u(0)={u0G,u0L}进行全时段仿真,将离散点处的仿真值作为相应优化变量的初值。
b.雅可比矩阵:将各约束分为线性部分和非线性部分,线性部分雅可比矩阵只需求解一次,由当前优化变量和约束解析表达式求出非线性部分雅可比矩阵后叠加[18-19]。离散生成的雅可比矩阵结构如图2所示,矩阵非零元个数为55916。
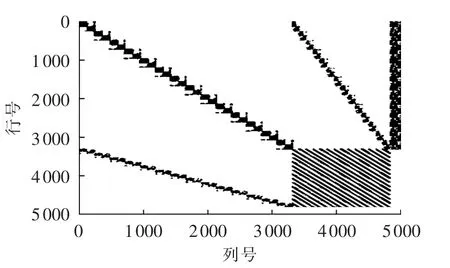
图2 雅可比矩阵结构Fig.2 Structure of Jacobi matrix
c.海森矩阵:采用拟牛顿法近似海森矩阵。求取算法采用基于有限内存的L-BFGS(Limited-memory BFGS)算法[20]。
4 算例测试
所用测试算例见表1,模拟故障为三相接地,仿真时长为1.8s,计算平台为Intel Xeon X5650 2.67GHzPC机。其中Case 118和Case 300分别由IEEE118和IEEE300标准测试系统修改得到;Case 678、Case 2 052和Case 2 383分别由2007年意大利、2005年日本和2000年波兰的实际电力系统简化得到。
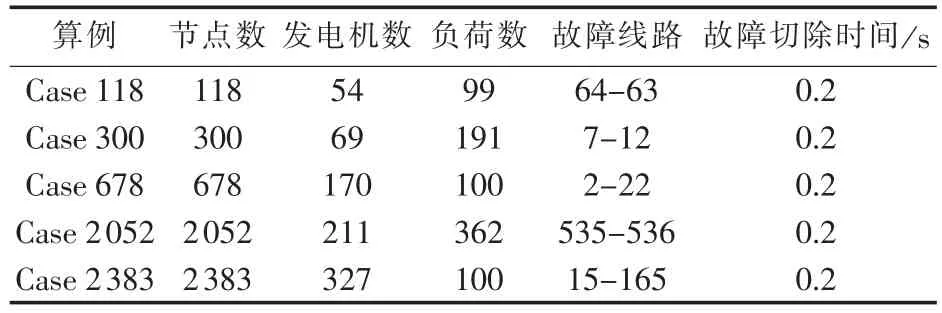
表1 测试算例Table 1 Cases for test
在计算时,有限元正交配置法配置3段共14个点,伪谱法使用14个点。为达到理想的精度,隐式梯形积分使用40个差分点,步长Δt=0.0375 s。
IPOPT是一个开源的优化软件包,使用C++编写,通过内点法求解大规模非线性优化问题[21]。
本文用IPOPT求解产生的NLP问题,为提高性能,利用Intel MKL库重新编译IPOPT。稀疏线性解法器使用 PARDISO[22],通过OpenMP并行化框架在多处理器主机上实现细粒度并行计算[23]。
4.1 有效性验证
在单线程下,分别使用隐式梯形积分、有限元正交配置和伪谱法对各算例进行计算,结果如表2所示。表中niter表示迭代次数,tCPU表示总计算时间,POBJ表示切除的总功率,“Fail”表示算例不收敛。
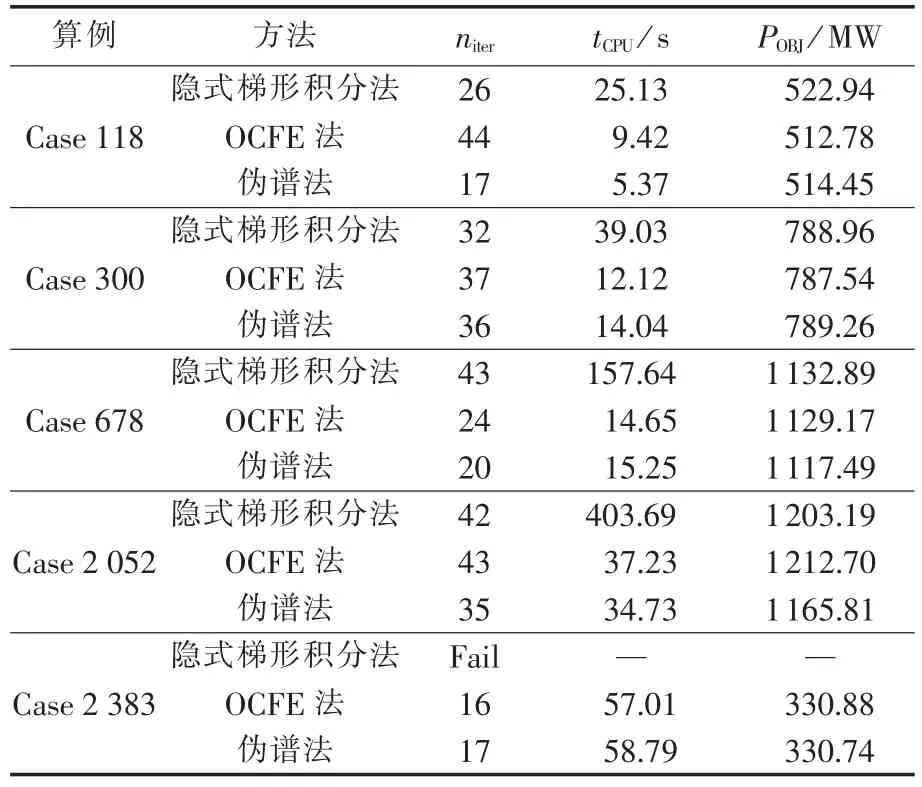
表2 不同离散方法下的优化结果Table 2 Optimization results for different discrete methods
优化完成后,根据计算出的切机切负荷量,使用4阶龙格-库塔算法(步长Δt=0.01 s)进行时域仿真,验证优化结果,均满足暂态稳定条件。图3是对118节点算例进行的仿真验证(点划线表示未施加控制时暂态不稳定的情况,实线表示优化后切机切负荷满足暂态稳定约束)。
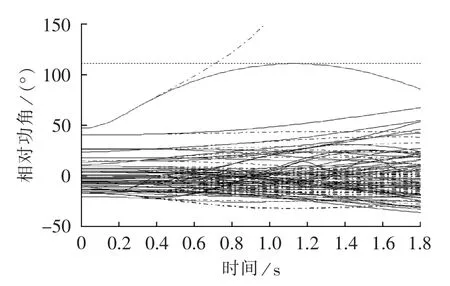
图3 Case118节点算例仿真验证Fig.3 Simulative verification by Case 118-bus system
在Case 118算例测试中,通过随机函数在约束范围内生成随机数作为控制参数 u(0)= [u0G,u0L]的初值,伪谱法求解均能收敛。表3给出了选取9组不同初值时,3种算法的迭代次数。可以看出,伪谱法对初值的要求不高,隐式梯形积分方法使用表中4组初值计算时无法收敛。在仿真验证中,伪谱法对初值的要求最低,具有很好的鲁棒性和收敛性。
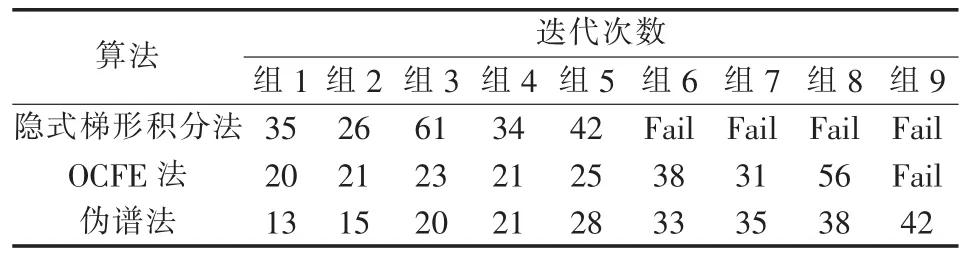
表3 不同初值下的迭代次数Table 3 Iteration times for different initial values
4.2 伪谱法与局部方法的对比
利用优化计算出的切机切负荷量和4阶龙格-库塔算法进行时域仿真生成的状态变量记为x~(t),优化后各离散点对应的状态变量记为X*k,定义状态变量误差矩阵E,其第k列表示为:
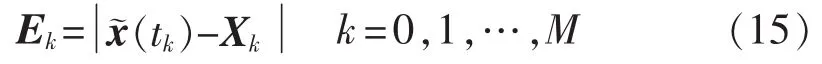
其中,tk为使用的正交配置点。取E各行的最大值(即各状态变量在配置点的最大误差)为误差向量vE={vi}iN=s1(Ns为状态变量总数)。 记状态变量误差:

采用40个差分节点时,隐式梯形积分方法的状态变量误差见表4。
表2中的正交配置方法均使用14个离散点,与隐式梯形积分方法相比,离散生成的NLP问题维数大幅降低,在计算时间上有明显的优势。此时,虽然有限元正交配置法和伪谱法使用了更少的离散点,但其误差精度仍高于隐式梯形积分方法(参考表4中配置点数为14的误差结果)。2种正交配置方法均远优于隐式梯形积分方法。
分别在配置点数为10、12、14、16下计算有限元正交配置法与伪谱法的误差,结果见表4(有限元正交配置法使用3个分段)。
在相同的配置点数下,有限元正交配置法和伪谱法的迭代次数和计算时间都是相当的,由于伪谱法的微分矩阵为稠密矩阵,单次迭代花费的时间略大于有限元正交配置方法。
从误差上看,伪谱法的精度略优于有限元正交配置法,这是因为伪谱法的离散化方程包含了整个区间上的配置点信息,而有限元正交配置法仅包含1个分段内的信息。
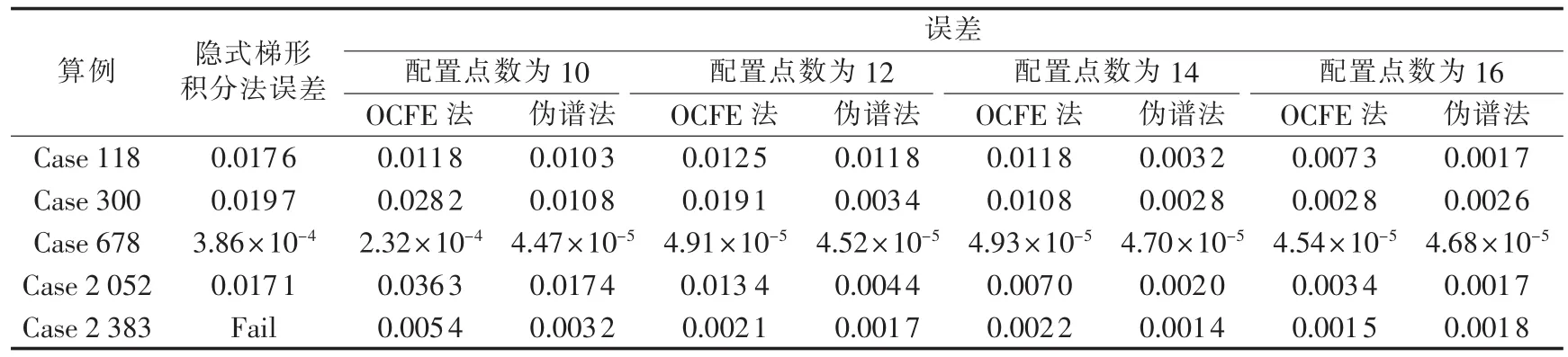
表4 配置点与误差Table 4 Collocation points and errors
4.3 并行加速
利用内点法求解稀疏大规模NLP问题时,大部分时间在求解原对偶系统线性方程组,对线性方程组求解实现细粒度并行可以大幅缩短计算时间。
PARDISO线性解法器可在共享内存SMP平台实现OpenMP并行加速。分别在线程数为1、2、4、8下统计伪谱法的优化运行时间,结果如表5所示。
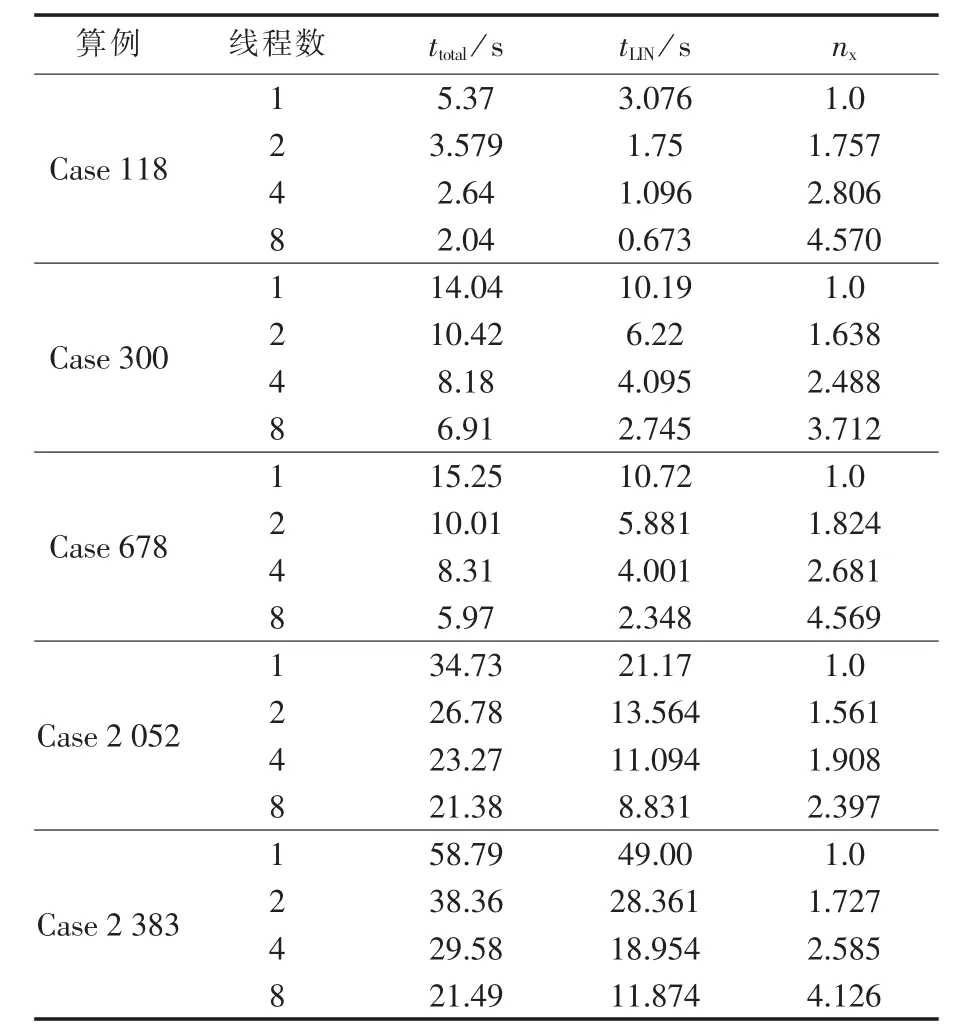
表5 不同线程下计算时间Table 5 Computation time for different thread numbers
并发线程数的改变主要影响线性方程求解效率,对算法其他部分影响很小。图4表示了线程数与线性方程求解时间占总时间百分比的关系,单线程下线性方程求解占用了大部分求解时间。随着线程数加倍,线程方程组求解时间所占的比例下降,虽然可以通过并行缩短计算时间,但通过增加线程获得的总体效率提升空间有限。线程数与线性方程求解加速比的关系见图5,当算例规模扩大时,加速比未表现出单调性的改变,加速比与算例规模大小的关系不明显。
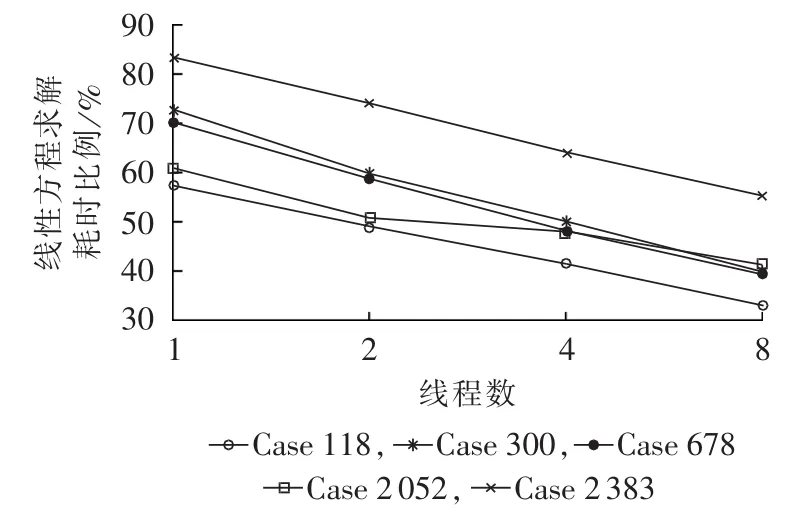
图4 线程数与线性方程求解占总时间百分比的关系Fig.4 Relationship between thread number and time percentage for solving linear equations
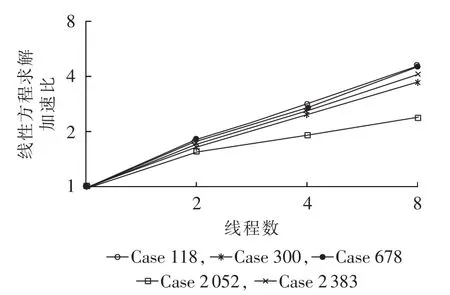
图5 线程数与线性方程求解加速比的关系Fig.5 Relationship between thread number and speedup ratio for solving linear equations
5 结语
本文使用求解最优控制问题的伪谱法计算电力系统紧急控制问题,并与局部联立法进行比较。不同规模电力系统的测试说明该算法具有以下特点。
a.在联立法中,伪谱法的计算性能和精度显著高于隐式梯形积分方法;在相同的配置点数下,伪谱法与有限元正交配置方法计算时间相当,而误差略小于有限元正交配置方法。伪谱法的应用为该问题求解带来了精度上的提升。
b.对于大规模系统,线性方程组求解成为计算性能瓶颈。利用OpenMP在共享内存平台上实现细粒度并行,可以大幅提高问题的求解效率。
