几乎无偏刘估计的不可容许性

王艳，华晶晶(.重庆大学数学与统计学院，重庆4033;.重庆电信研究院，重庆40336)

几乎无偏刘估计的不可容许性

王艳1，华晶晶2
(1.重庆大学数学与统计学院，重庆401331;2.重庆电信研究院，重庆401336)

考虑了线性回归模型中，在Fisherian和Mahalanobis损失函数下，几乎无偏刘估计对于最小二乘估计的不可容许性;结论表明:几乎无偏刘估计在Mahalanobis损失函数下是不可容的;最后进行了数值模拟来表明结果.

几乎无偏刘估计;最小二乘Mahalanobis损失函数;Fisherian损失函数

0　引言

考虑如下线性回归模型:

其中y是n×1的观测向量，X是秩为p的n×p设计矩阵，β是p×1未知参数向量，ε是n×1随机误差向量，β的普通最小二乘估计(OLSE)如下:

最小二乘估计过去很长一段时间被认为是线性模型中最好的估计，存在复共线性时，最小二乘估计便失去了它的最优地位.为了克服复共线性，很多学者做了大量的努力，有一种方法是考虑有偏估计，如岭估计［1］、刘估计［2］、两参数估计［3-4］.

Liu［2］提出的刘估计定义如下:

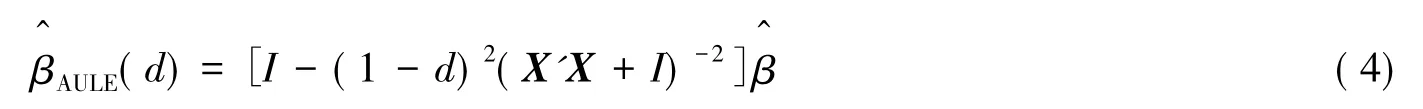
Akdeniz和Kaciranlar［6］讨论了在均方误差意义下，AULE在一定条件下优于OLSE.

尽管在均方误差意义下，在一定条件下AULE优于OLSE，但更想知道在其他准则下是否还有这一结论.此处在Fisherian和Mahalanobis损失函数下比较了这两种估计的优越性.

第2部分给出了线性模型的典则形式，第3部分在Fisherian和Mahalanobis损失函数下比较了AULE和OLSE，最后进行了数值模拟和结论标注.

1　模型和估计

考虑线性模型(1)，令Λ=diag(λ1，λ2，…，λp)对角线上元素是X'X的特征值，T是由X'X的特征向量组成的p×p矩阵，满足T'X'XT=Λ，TT'=T'T=I，λ1≥λ2≥…≥λp.原来的回归模型可写成如下典则形式:

其中Z=X T，α=T'β.显然Z'Z=Λ，最小二乘估计和几乎无偏估计写成如下形式:

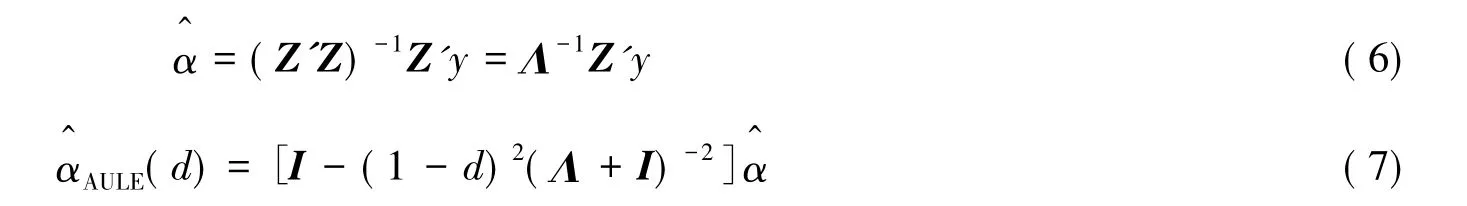
2　Fisherian和Mahalanobis损失函数下的风险比较

这一部分将比较AULE和OLSE在Fisherian和Mahalanobis损失函数下的风险.

2.1 Fisherian损失函数下的风险比较

由于ε～N(0，σ2I)，有，即表示β的协方差矩阵.

OLSE的Fisherian损失函数是

AULE的Fisherian损失函数是

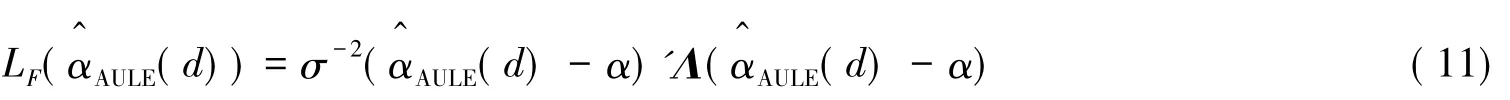
定理1在Fisherian损失函数下，AULE优于OLSE，当且仅当

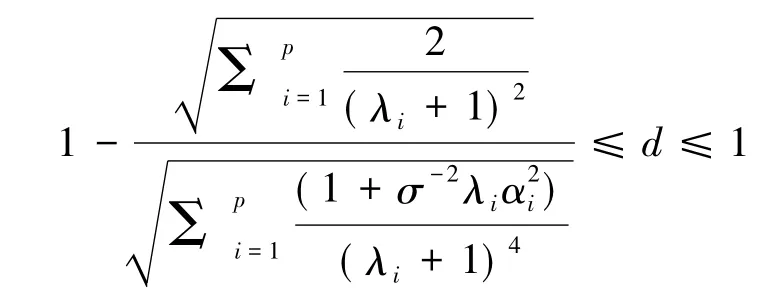
证明由方程(10)可得出

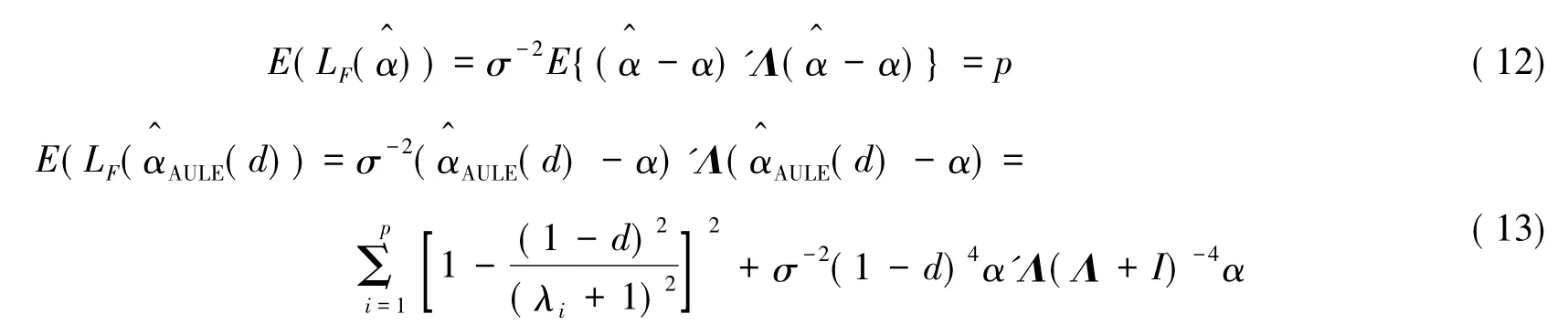
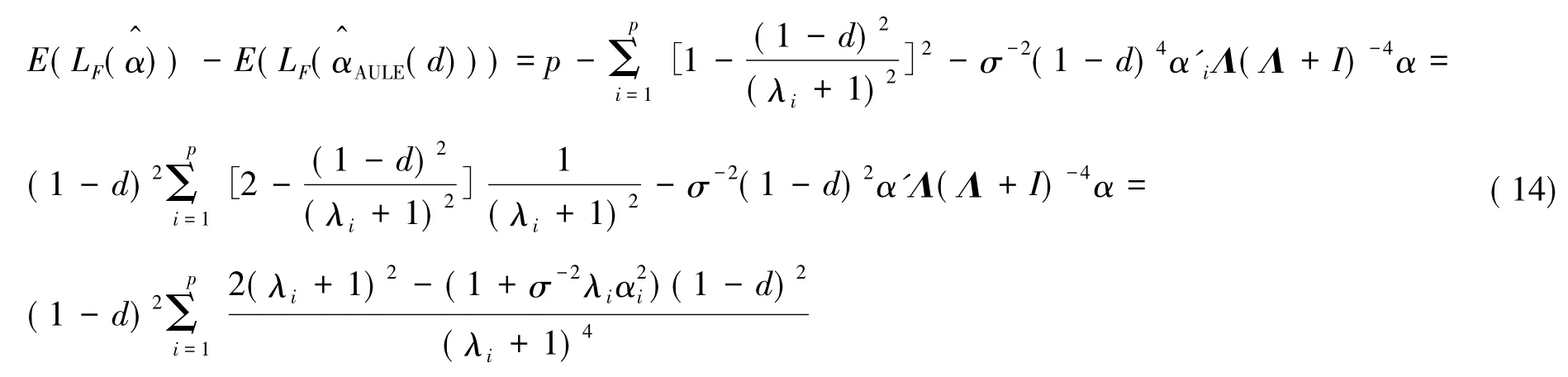
2.2 Mahalanobis损失函数下的风险比较

所以

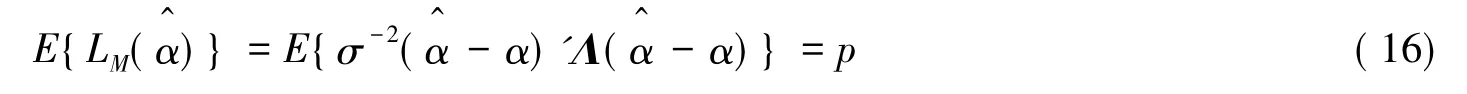
同理可得

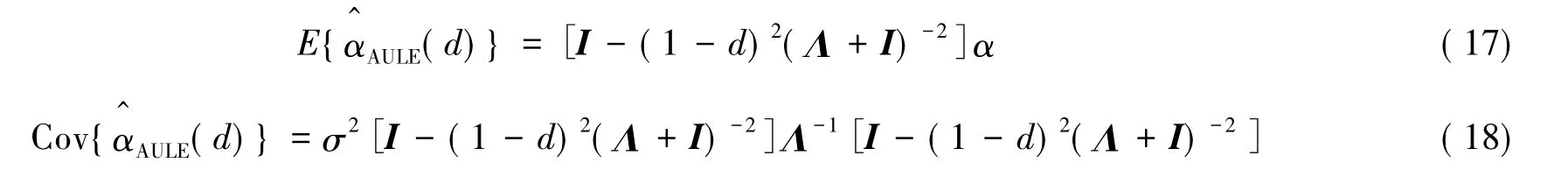
因此有

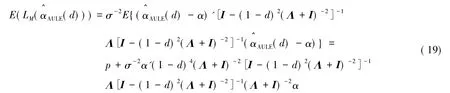
由方程(16)、(19)，得到

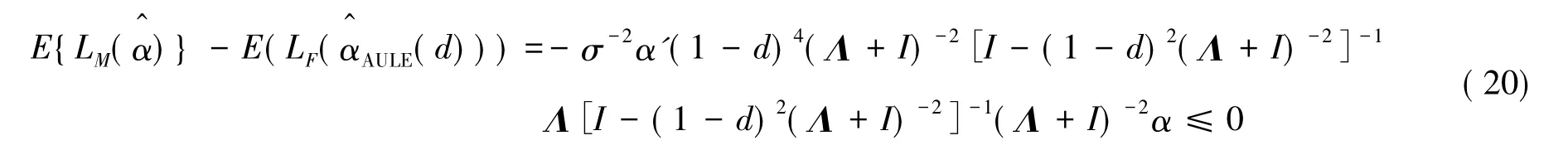
因此由如下定理2.

定理2在Mahalanobis损失函数下AULE对于OLSE是不可容的.

3　数值模拟

为了进一步表明理论结果，在这部分进行一个数值模拟.根据McDonald和Galarneau［7］和Liu［8］，解释变量如下:

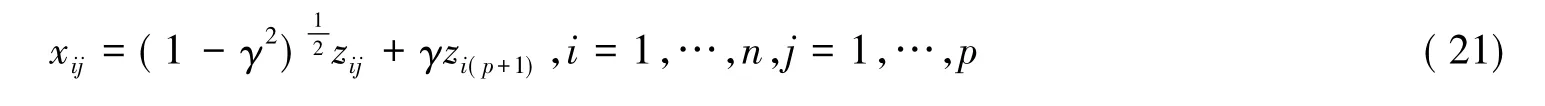
其中zij和zi(p+1)是独立标准正态随机变量.给定γ，两解释变量之间的相关系数是γ2.考虑n=25，p=4，γ=0.8，0.9，0.99，观测变量如下产生(式(22)):

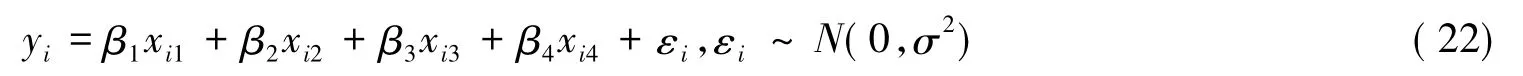
表1～表6给出了估计值的Fisherian损失和Mahalanobis损失.

表1　γ=0.8，κ=10.391 4，OLSE和AULE的Fisherian损失

表2　γ=0.9，κ=48.495 1，OLSE和AULE的Fisherian损失

表3　γ=0.99，κ=469.315 4，OLSE和AULE的Fisherian损失

表4　γ=0.8，κ=10.391 4，OLSE和AULE的Mahalanobis损失

表5　γ=0.9，κ=48.495 1，OLSE和AULE的Mahalanobis损失

表6　γ=0.99，κ=469.315 4，OLSE和AULE的Mahalanobis损失

从表1～表6所给出的模拟结果来看，随着复共线性的增加，AULE和OLSE的损失函数增加;随着σ2的增加;AULE的Fisherian损失和Mahalanobis损失减少.由表4～表6，OLSE总是优于AULE，与定理2相吻合.

［1］HOERL A E，KENNARD RW.Ridge Regression:Biased Estimation for Non-orthogonal Problems［J］.Technometrics，1970(12): 55-67

［2］LIU K.A New Class of Biased Estimate in Linear Regression［J］.CommunStat Theory Methods，1993(22):393-402

［3］ÖZKALE M R，KAIRANLAR S.The Restricted and Unrestricted Two-Parameter Estimators［J］.CommunStat Theory Methods，2007 (32):1009-1020

［4］汪国平.线性模型中的一类新的k-d类估计［J］.重庆工商大学学报:自然科学版，2013，30(7):12-15

［5］IRAY GÜ，SAKALLOLU.Inadmissibility of the Liu Estimator to the Ordinary Least Squares Estimator［J］.Advances and Applications in Statistics，2010(19):21-32

［6］AKDENIZ F，KAÇIRANLAR S.On the Almost Unbiased Generalized Liu Estimator and Unbiased Estimation of the Bias and MSE［J］.Commun Stat Theory Methods，1995(24):1789-1797

［7］MCDONALD M C，GALARNEAU D I.A Monte Carlo Evaluation of Ridge-type Estimators［J］.Journal of the American Statistical Association，1975(70):407-416

［8］LIU K.Using Liu-Type Estimator to Combat Collinearity［J］.CommunStat Theory Methods，2003(32):1009-1012

Inadmissibility of the Almost Unbiased Liu Estimator

WANG Yan1，HUA Jing-jing2
(1.School of Mathematics and Statistics，Chongqing Universtity，Chongqing 401331，China; 2.West Institute，China Academy of Telecommunication Research，Chongqing 401336，China)

This paper considers the admissibility of the almost unbiased Liu estimator to the ordinary least squares estimator of linear regression model in the Fisherian and Mahalanobis loss functions.The results show that the almost unbiased Liu estimator is inadmissible under Mahalanobis loss function.Finally，a simulation study is given to show the theoretical results.

almost unbiased Liu estimator;ordinary least squares estimator;Mahalanobis loss function; Fisherian loss function

O212.1

A

1672－058X(2015)09－0026－05

10.16055/j.issn.1672－058X.2015.0009.007

2015－01－10;

2015－02－20.

王艳(1990-)，女，湖北荆州人，硕士研究生，从事参数估计与变量选择研究.