具有脉冲扩散和扩散时滞的单种群模型研究*
2015-09-16黄玲智重庆师范大学数学学院重庆401331
黄玲智(重庆师范大学数学学院,重庆401331)
具有脉冲扩散和扩散时滞的单种群模型研究*
黄玲智
(重庆师范大学数学学院,重庆401331)
研究了两斑块间具有脉冲扩散和扩散时滞的对数增长单种群模型,利用脉冲微分方程比较原理和离散动力系统频闪映射理论,得到了系统持久性和周期解的全局稳定性的充分条件.
脉冲扩散;扩散时滞;持久性;全局稳定性
0 引言
近年来,很多学者对种群的扩散现象进行了深入的研究[1-3].扩散是自然界很普遍而且有规律的现象,比如,鸟儿在冬季来临时会进行迁徙,但是它们并不在其他季节扩散.种群在扩散过程中会出现一些损失而且扩散需要时间.
考虑具有脉冲扩散和扩散时滞的对数增长单种群模型:
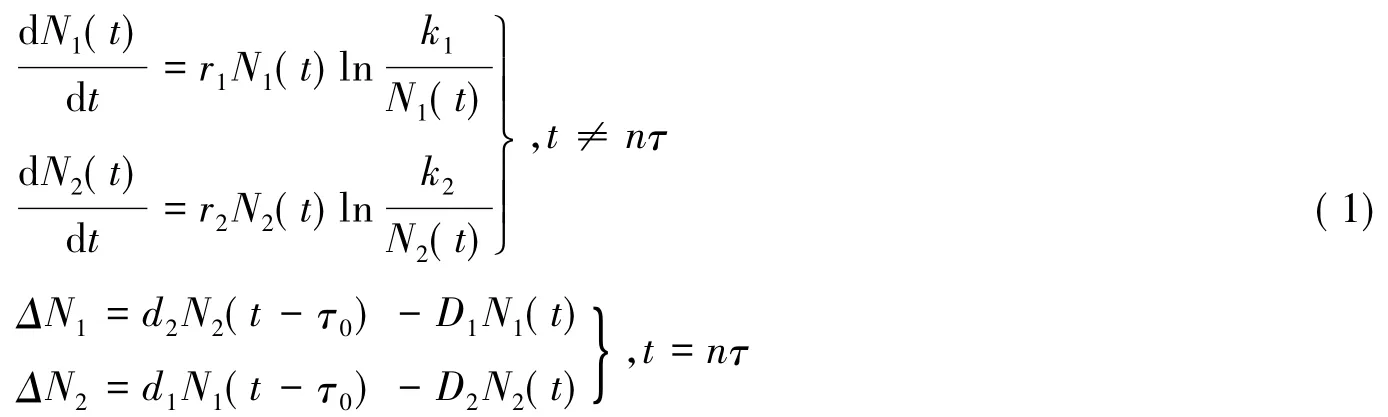
其中Ni(t)(i=1,2)表示t时刻第i个斑块的种群密度,ri(i=1,2)表示第i个斑块的内禀增长率,Di(i=1,2)表示种群Ni从第i个斑块的移出率,di表示种群Ni迁移到第i个斑块的迁入率,在这里假设0≤di<Di<1,也就说明在斑块间的扩散过程中,种群存在损失,τ0表示种群在扩散过程中所用的时间.
1 预备知识
考虑如下非线性脉冲系统:

其中r,k表示正数,0<p<1.
引理1[4]系统(2)存在唯一全局渐进稳定的正周期解.
引理2[5]令是连续映射并在内具有一阶导数,假设DF(0)存在并且另外假设:
(A)当x>0时,DF(x)>0.
(B)当0<x<y时,DF(y)<DF(x).
如果F(0)=0,令λ=ρ(DF(0)).如果λ≤1,那么对一切x≥0,Fn(x)→0,n→∞;如果λ>1,那么,或者对一切x>0,Fn(x)→∞,n→∞;或者F存在唯一非零不动q.对于后一种情况q>0并且对一切x>0,有Fn(x)→q,n→∞.
如果F(0)≠0,对一切x≥0,或者Fn(x)→∞,n→∞;或者F存在唯一不动q.对于后一种情况q>0,并且对一切x>0,有Fn(x)→q,n→∞.
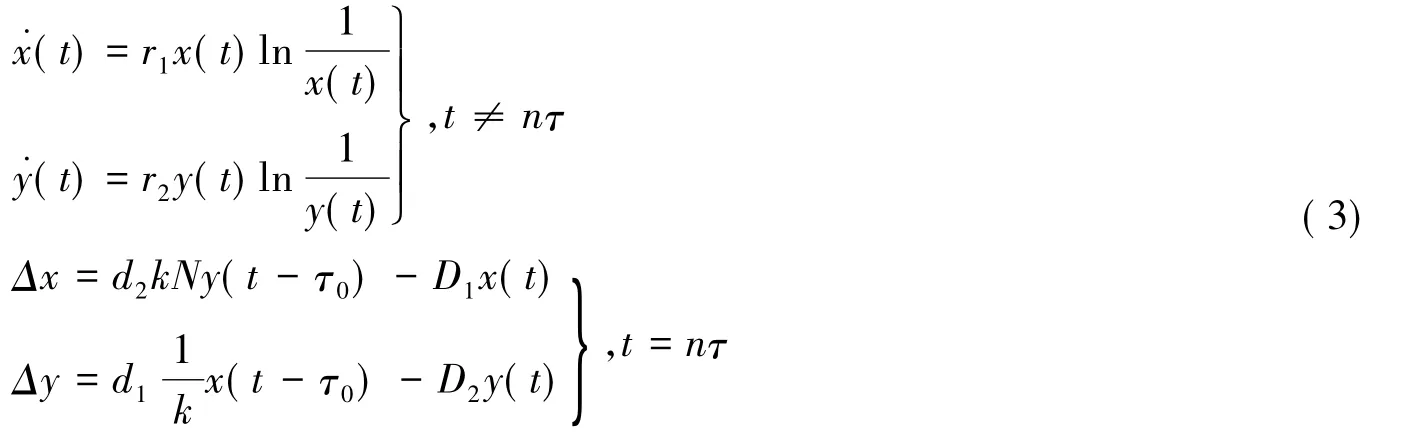
对系统(3)的前两个方程,在相邻脉冲点之间进行积分得
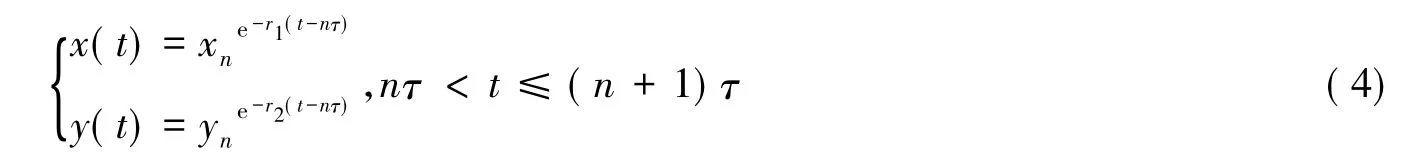
考虑系统(3)的后两个方程,得到如下的频闪映射:
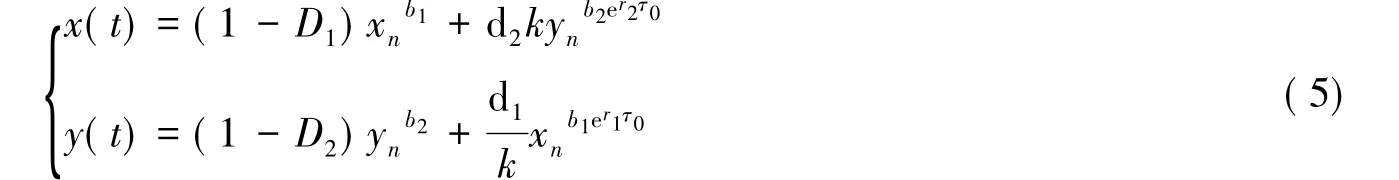
2 持久性
定理1系统(1)是持久性的.
证明首先证明系统(1)一致有上界.令(N1(t),N2(t))是系统(1)的任意解,初值N(0)>0,V(t)= N1(t)+N2(t),λ0=min{r1,r2},当t≠nτ时,有
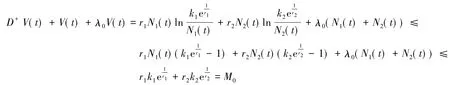
最后证明系统(1)的所有解一致有下界.当di≥0(i=1,2),有
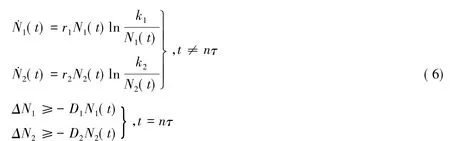
在这个系统(6)中N1(t),N2(t)没有任何联系,可以将它们独立出来.

考虑系统(7)的脉冲比较系统:

同理可得,对于充分小的ε>0,存在一个T2>0,有
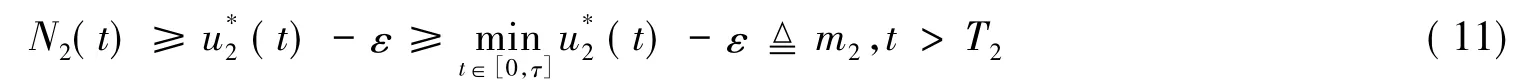
定理1的证明结束.
3 正周期解的稳定性
首先证明系统(5)存在唯一的正不动点,即系统(1)存在唯一的正周期解.
定理2当(H1):D1≥d2k和(H2):b1+b2+d1d2<1成立时,系统(5)存在唯一的正不动点.
证明由系统(5),得到以下系统:

由系统(12)得到
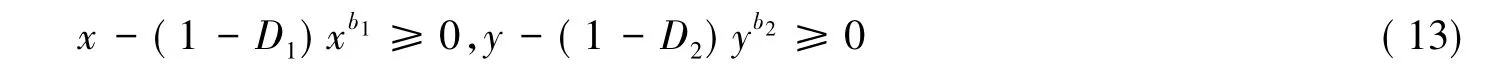
由系统(12)可得
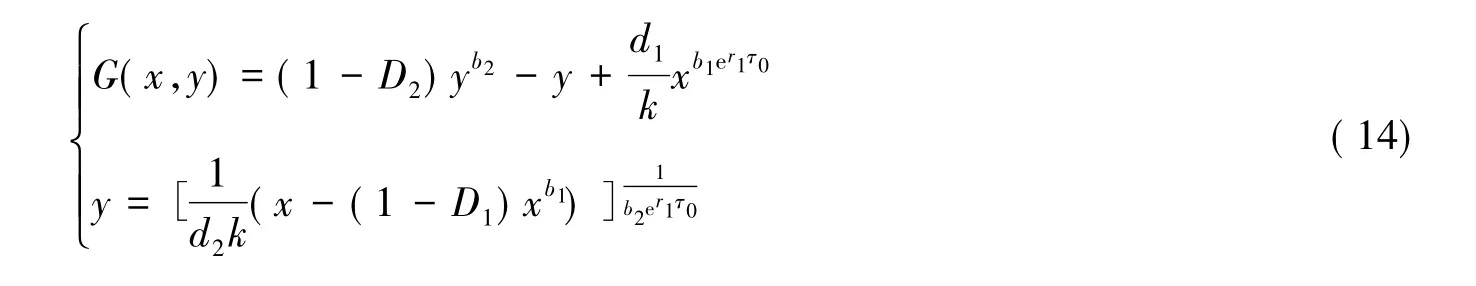

存在(x*,y*)满足,使得

通过式(14)可得
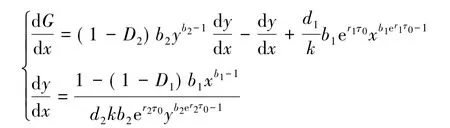
故
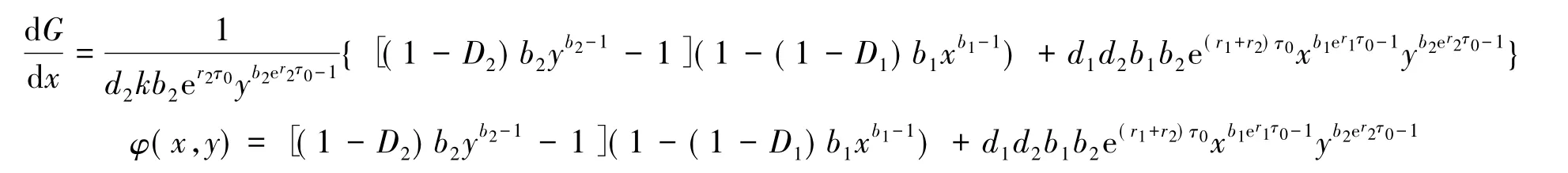
则
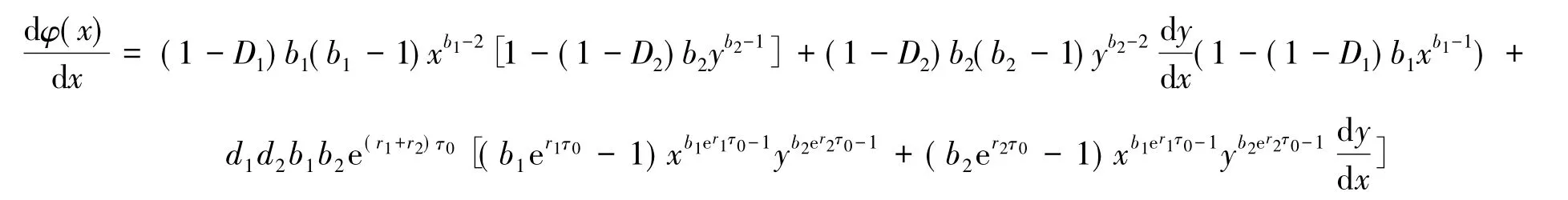
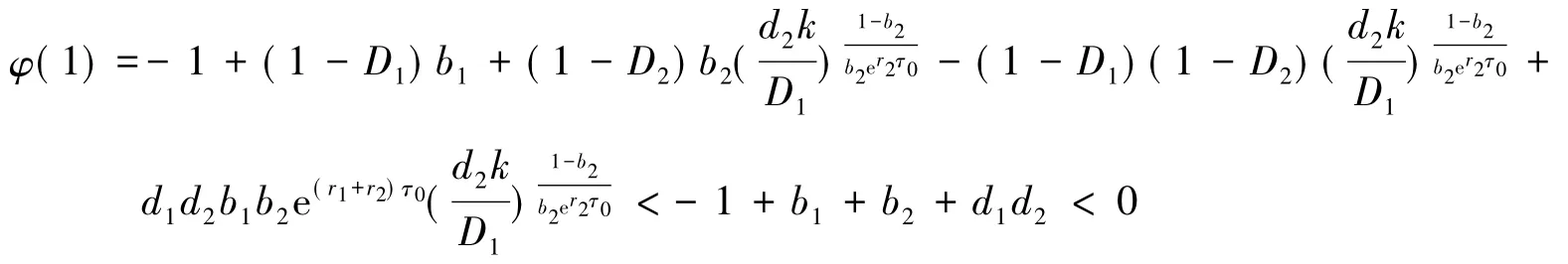
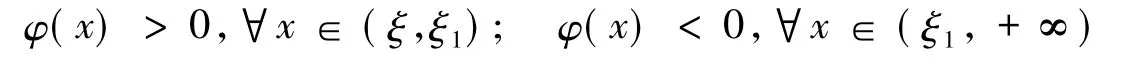
于是有
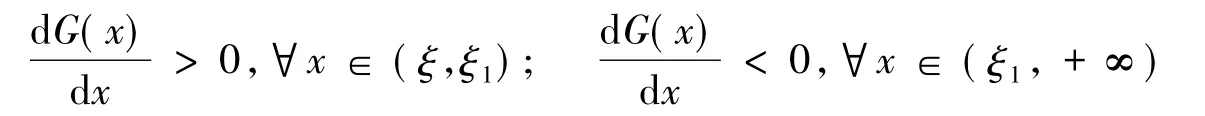
接下来,将证明系统(5)的正不动点(x*,y*)是全局稳定的,也就是系统(1)的正周期解是全局渐进稳定的.
定理3如果(H1)和(H2)成立,对于每一个(x,y)>(0,0),都有
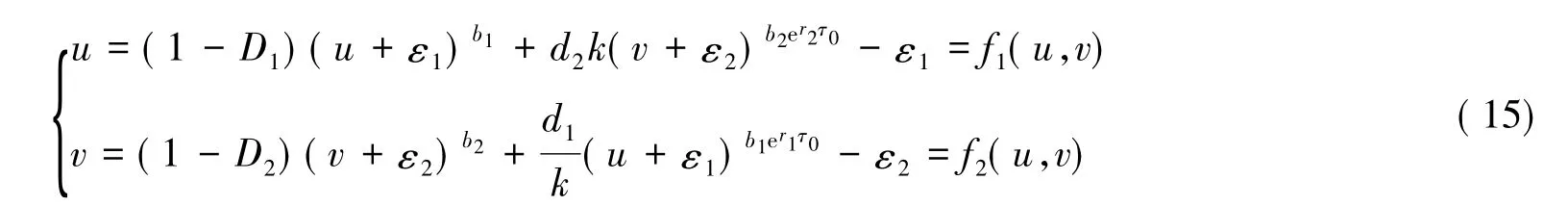
因为
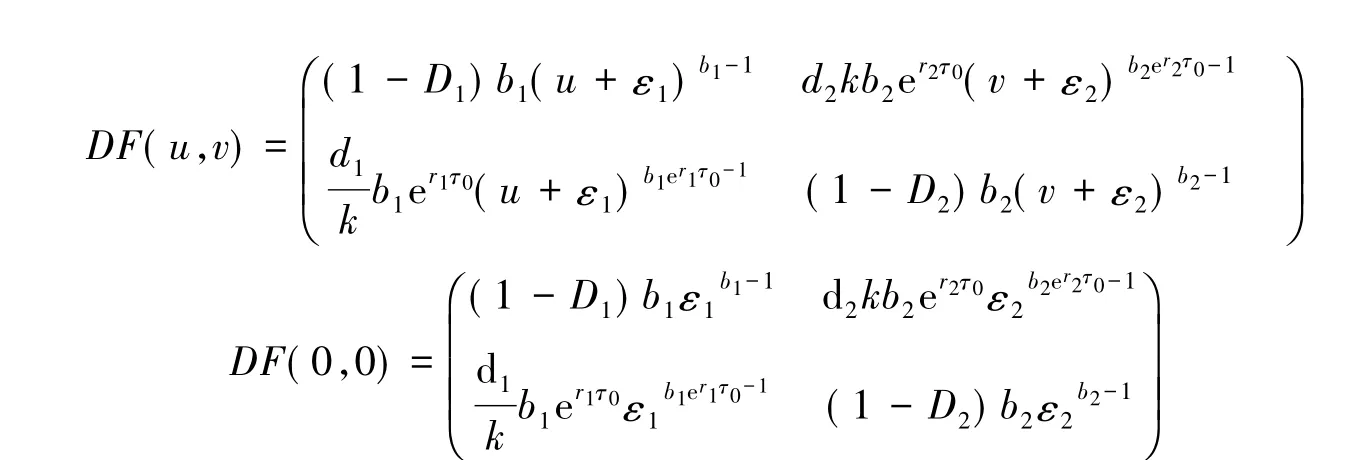
[1]WANG LM,LIU Z J,JH.Impulsive Diffusion In Single Species Model[J].Chaos,Solitons and Fractals,2007(33):1213-1219
[2]WAN H Y,ZHANG L,LIH L.A Single Species Modelwith Symmetric Bidirectional Impulsive Diffusion and Dispersal Delay[J].Applied Mathematics,2012(3):1079-1088
[3]JIAO J J,YANG X S,CAI SH.Dynamical Analysis of a Delayed Predator-prey Model with Impulsive Diffusion Between Two Patches[J].Mathematics and computers in simulation,2009(80):522-532
[4]JIA JW,LI C H.A Predator-prey Gompertz Model with Time Delay and Impulsive Perturbations On the Prey[J].Discrete Dynamical in Nature and Society,2009(2009):15-19
[5]AMITH H L.Cooperative System of Differential Equations with Concave Nonlinearities[J].Nonlinear Anal TMA,1986(10): 1037-1052
Research on a Single Species Model with Impulsive Diffusion and Dispersal Delay
HUANG Ling-zhi
(School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China)
This paper researches a single species model in logarithmic growth with impulsive diffusion and dispersal delay.Using the comparison theorem of impulsive differential equation and the discrete dynamical system,the permanent sufficient conditions of the system is obtained,and the system has a global stability positive periodic solution.
impulsive diffusion;dispersal delay;permanent;global stability
O175
A
1672-058X(2015)09-0005-05
10.16055/j.issn.1672-058X.2015.0009.002
2015-03-15;
2015-04-28.
国家自然科学基金(11471061);重庆市自然科学基金(CSTC2014jcyjA40004).
黄玲智(1991-),女,湖南怀化人,硕士研究生,从事微分方程及其应用研究.
