基于仿真软件的小波分析课程教学方法

黄洪全　任家富　陈光柱

成都理工大学　四川成都　610059

基于仿真软件的小波分析课程教学方法

黄洪全任家富陈光柱

成都理工大学四川成都610059

针对小波分析课程内容多且难度大的特点，结合Matlab软件强大的工具箱和GUI功能，以数据压缩为实例，将小波理论分析、代码编辑和用户界面进行了有机融合，实现了理论与实践的完整统一，使学生通过图形化直观认知、快速编程验证及理论分析工程实际问题来实现该课程的轻松学习。

小波分析；Matlab；教学方法

小波变换是空间（时间）和频率的局部变换，被称为“数学显微镜”，能更加有效地提取和分析信号的局部特性，故在许多领域，如信号分析、计算机视觉、视频图像分析、图像识别、数据压缩和传输、故障诊断等领域有着重要的应用。［1］因此，有许多理工高校的高年级课程都已开设小波分析这门课程或者在其他课程中涉及小波分析内容，以便为学生搭建进行信号分析研究的更高平台。

小波分析涉及的内容丰富、知识点多，而且抽象、难于理解。在以往教学中，常常将小波分析这样的课程按数学理论对待，主要进行公式的复杂推导，这种教学方式最终会使学生感到枯燥乏味，难免课程结束后绝大部分学生对小波分析内容一知半解甚至对其基本思想都不能了解。事实上，小波分析理论的产生是为工程而诞生的，若能结合实际工程应用及解决工程的效果教学，定会加快和加深对小波分析的理解，甚至能让学生在课堂上“愉快”地采用小波理论进行信号处理。

本校课程组针对小波分析难以教学的特点进行了积极探索和实践，结合功能强大的Matlab wavelet这一工具［2，3］，将理论分析、工程应用及实验环节进行了有效融合，取得了较明显效果。下面以小波分析用于数据压缩的一个工程应用为例，说明如何在Matlab上实现小波分析的快速学习。

1　小波压缩算法

小波分析方法可很好地刻画复杂信号［3-6］，并可通过显微镜似的方法提取或保留重要细节。在限定的误差范围内，提取各子频带的重要小波系数，即可作为压缩后的数据信息，进而实现数据压缩。

1.1压缩方法

将平方可积空间L2（R）分解为小波空间｛Wj｝j∈Z和尺度空间｛Vj｝j∈Z两个子空间［4，5］，并有：

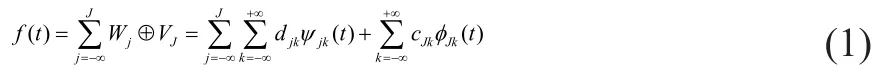
小波压缩基于以上原理，将各子频带的重要小波系数和尺度系数作为压缩后信息数据，解压时由这些数据和相应的小波函数及尺度函数进行信号的重构。只要选择的系数合理，重构的信号可以任意精度逼近原始信号。设原始信号为f（t），重构的信号为提取重要系数步骤如下。

第一步：设定各频带下的阈值：

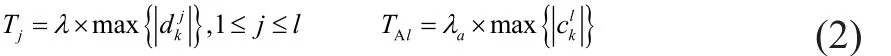
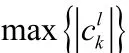
第二步：进行系数的阈值处理：

将大于阈值的系数保留，否则置为零，求取经l层阈值处理后的小波系数和第l层尺度系数，提取非零系数，并将函数表示为：

第三步：计算二范数相对误差e，修正比例系数λ：

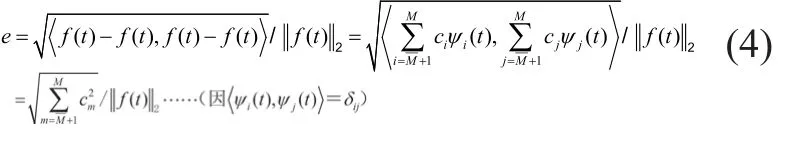
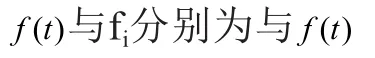
需要指出的是，根据各信号频带系数的分布特点，每个子频带的比例系数λ可选取不同的值；也可采用全局阈值法，即所有子频带使用同一个阈值。

1.2压缩的快速算法

设原始信号f（t）的离散形式为f（k），按Matlab快速分解算法［4，5］。求得各子层小波系数，按上述方法进行阈值处理和计算二范数误差e以及参数调整。这样由滤波器系数h、g、非零系数d及末层低频系数fl，k就构成信号f（k）压缩后的数据信息。

2　数据压缩的代码实现

采用Matlab工具箱内的函数快速实现小波分解、小波及尺度系数获取，避免了繁杂的程序代码。［6］编制如下快速实现数据压缩的代码，为教学提供参考。

2.1初始化

初始化原始信号s。设置比例系数λ和相对误差e0。

2.2小波分解及提取系数：

［c，l］=wavedec（s，5，'db4'）；%对s采用db4小波进行5分解。

d5=detcoef（c，l，5）；d4=detcoef（c，l，4）；d3=detcoef（c，l，

3）；d2=detcoef（c，l，2）；d1=detcoef（c，l，1）；

a5=appcoef（c，l，'db4'，5）； % d1～d5为提取的1～5层小波系数，a5为第5层尺度系数。

2.3求1～5层小波系数阈值t1～t5，第5层尺度阈值ta5按公式（6）

t5=λ*max（abs（d5））；t4=λ*max（abs（d4））；t3=λ*ma x（abs（d3））；t2=λ*max（abs（d2））；t1=λ*max（abs（d1））。

2.4求阈值处理后的系数，第五层尺度系数A5按如下处理，第1～5层小波系数D1～D5方法类似

2.5重构各子频带信号

aa5=wrcoef（'a'， C，l，'db4'，5）；dd5=wrcoef（'d'，C，l，'db4'，5）；dd4=wrcoef（'d'，C，l，'db4'，4）；

dd3=wrcoef（'d'，C，l，'db4'，3）；dd2=wrcoef（'d'，C，l，'db4'，2）；dd1=wrcoef（'d'，C，l，'db4'，1）；

S= aa5+ dd5+ dd4+ dd3+ dd2+ dd1。% dd1～dd5为阈值处理后重构的1～5层高频信号，aa5为阈值处理后重构的第5层低频信号，S为阈值处理后重构的信号，即原始信号s的近似信号。

2.6求二范数相对误差e

e=（sum（（S'-s）.^2））^0.5/（sum（s.^2））^0.5；

若相对误差e与e0相近则S为原始信号s的解压后信号，S信号各子频带的非零系数与相应滤波器g，h系数作为s信号压缩后的数据信息。否则，重置比例系数λ重复以上过程。

2.7求子频带系数的非零个数J，以了解大致压缩比J=0；for i=1:length（C）

if abs（C（i））＞0；J=J+1；

end；

end；

2.8绘出信号s与S以示解压后信号的恢复效果

plot（s， '.'）；hold on； plot（S， 'r-'）；legend（'s'， 'S'）；xlabel（'c hannel'）；ylabel（'counts'）

图1所示为55Fe放射源的X射线能谱图，道址数为1024，1-1024道的总计数为20 000，谱线中段是55Fe 的Kα（5.9kev）和Kβ（6.49kev）特征峰。图2给出了压缩前后信号s与S对比情况，给出的比例系数λ=0.15，非零系数个数J为361，二范数相对误差e为0.085 7，压缩比大致为102 4/361=2.8，可见Kα（5.9kev）和Kβ（6.49kev）两特征峰保持较好。

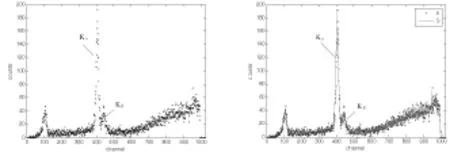
图1　55Fe放射源的X射线能谱　图2 能谱压缩前后对比

3　压缩的Matlab GUI实现

采用Matlab GUI用户接口工具，可将所分析的数据导入，调用相应的分析模块加以运算，处理过程简单、方便、高效，给予快速、直观的视觉效果。［7-9］学生使用GUI工具学习小波分析理论并解决实际工程问题，可谓是在享受这一学习过程，会倍感快乐和信心十足。仍以55Fe放射源的X射线能谱压缩分析为例，采用GUI接口并结合如上代码快速实现数据压缩的过程如下。

（1）数据处理前的准备。在Matlab命令符下输入原始信号s=［ ］； 使用save命令将数据s保存在Matlab的某一路径下，重新命名为mydatays: save mydatays s。

（2）在Matlab/start/toolboxes/wavelet打开wavelet toolbox main menu， wavelet 1-d；然后通过file/load/ signal找到文件mydatays装载数据。

（3）选择db 4 wavelet，level 5，点击analyze。可以看到小波空间1～5层子频带信号d1～d5及尺度空间子频带信号a5。d1～d5为高频信号，表示信号的细节；a5为低频信号，表示信号的轮廓（如图3所示）。

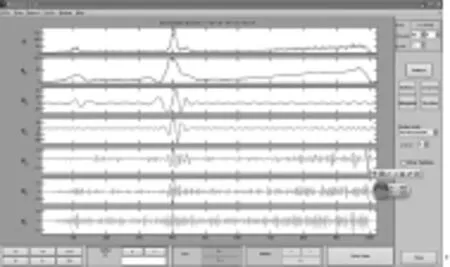
图3　各子频带信号

（4）选择tree mode，以显示信号分解的树状结构。如图4所示，左图为树状结构，右图分别为原始信号s及其低频信号a5，点击任意树枝节点可显示该节点处的子频带信号。选择show and scroll可显示小波系数柱状图（如图5-a所示），最上一图为原始信号与第5层低频信号，居中图为第5层高频（细节）信号，底部图为1～5层小波系数；如图5-b所示，最上一图为原始信号与第1层低频信号，其余两图与图5-a相同。选择separate mode可显示各层低频信号（a1～a5）、各层高频信号（d1～d5）、原始信号s及各层小波系数（cfs），如图6所示。

图4　信号分解的树状结构

可以看出，高频部分对应的细节信号多为噪音，只保留其重要小系数即可，这也是该信号可以压缩的依据。

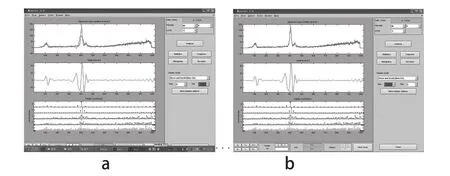
图5　信号分解后的小波柱状图

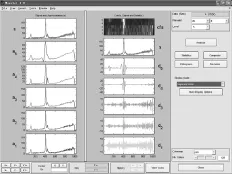
图6　信号分解后的各频带信息

（5）点击c o m p r e s s，设置各层小波系数阈值（thresh）。仍按λ=0.15，在命令符处由代码max（ ）求得各层最大值，如max（abs（d1））表示求第一层最大小波系数，然后求得d1～d5的系数阈值分别为2.87，4.271，4.795，23.478，32.505；阈值也可通过拖动阈值线来设置。如图7所示，图7-a左半为d1～d5的系数分布及阈值线；中上图为原始信号与压缩后信号对比情况，中下两图分别为原始小波系数及阈值处理后小波系数的颜色表示，值越大亮度越高；图7-b为设置d1阈值线的示意图，其它细节信号的阈值线设置类似。压缩后零系数占65.81%，能量为原来的99.21%，可计算压缩比大致也为2.8，与前面代码计算一致。图8所示为压缩后信号S与原始信号s的残差，残差在Kα（5.9kev）和Kβ（6.49kev）特征峰附近相对突出，特征峰必有一定程度损失。

设置各层小波系数阈值可按全局设定（global thresholding），如图9、图10所示。全局阈值设置为3.687，压缩后零系数仍占65.81%，压缩比大致也为2.8；能量为原来的99.72%，比图8情况所保持的能量99.21%有提高。残差大致表现出均值为零的噪音，在Kα（5.9kev）和Kβ（6.49kev）特征峰附近残差没有明显特征，表明剔掉的几乎是噪音，峰形特征损失必定很小。总体上，在相同压缩比为2.8的情况下，按全局设定阈值比按λ=0.15设置各层阈值的压缩性能好。

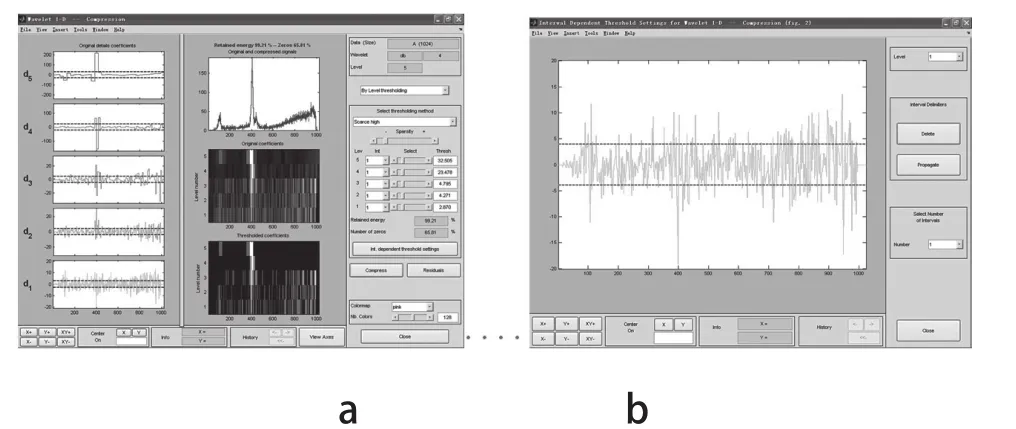
图7　各层阈值设定

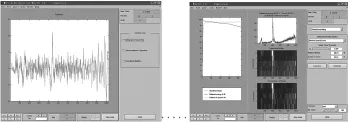
图8　压缩后的残差　图9 阈值的全局设定

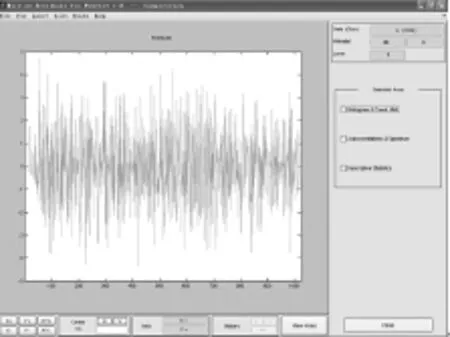
图1　0 压缩后的残差（全局设定）

以上以55Fe放射源X射线能谱的小波压缩工程应用为例，给出了小波理论分析、算法研究、快速编程及基于图形窗口的数据处理与分析过程，这一将理论分析、工程应用及实验环节进行有效融合的教学方式，定会使学生快速和深刻地理解小波分析理论，甚至能让学生在课堂上“愉快”地采用小波理论进行信号处理。

4　结束语

小波分析课程内容多，难度大，按传统数学推导的单一教学方法难以达到好的教学效果。若能结合实际工程应用问题，采用Matlab软件强大的工具箱和GUI功能，将小波理论分析、代码编辑和用户界面进行有机融合，实现理论与实践的完整统一，使学生通过图形化直观认知、快速编程验证及理论分析工程实际问题来进行课程的学习，定会加快和加深对小波分析的理解，甚至能让学生在课堂上“愉快”地采用小波理论进行信号处理的举一反三，可谓是在“享受”这一学习过程，会倍感快乐和信心十足。

［1］ 冉启文.小波分析方法及其应用［M］.哈尔滨:哈尔滨工业大学出版社，1999.

［2］ 葛哲学，沙威.小波分析理论与MATLAB R2007实现［M］.北京:电子工业出版社，2007.

［3］ 李建平.小波分析与信号处理-理论、应用及软件实现［M］.重庆:重庆出版社，1997.

［4］ 彭启琮.信号分析［M］.北京:电子工业出版社，2006.

［5］ Ingrid Daubechies，李建平，杨万年译.小波十讲［M］.北京:国防工业出版社.2004.

［6］ 董长虹.Matlab小波分析工具箱原理及应用［M］.北京:国防工业出版社.2004.

［7］ 陈垚光，毛涛涛，王正林.精通MATLAB GUI设计［M］.第1版.北京:电子工业出版社，2008.

［8］ 李京秀，陈白生.基于Matlab图形用户界面 GUI的电路仿真实验的制作［J］.电气电子教学学报，2004，26（4）:99-101.

［9］ 金波.基于Matlab的信号与系统实验演示系统［J］.实验技术与管理，2010，27（12）:104-107.

The Teaching Method of Wavelet Analysis Based on Simulation Software

Huang Hongquan， Ren Jiafu， Chen Guangzhu
Chengdu University of Technology， Chengdu， 610059， China

Wavelet analysis course has too much difficult content， according to this characteristic， the powerful toolbox and GUI of Matlab software are applied. Take data compression for example， the theory analysis of wavelet， code editing and user interface are linked in one organic whole， to achieve a complete unity of theory and practice， so that students can learn this course easily through the graphical intuitive cognitive， fast programming verification and theoretical analysisabout practical engineering problems.

wavelet analysis； Matlab； teaching method

2014-09-30

黄洪全，博士，副教授。任家富，本科，教授。

四川省教育厅重点项目高等教育人才培养质量和教学改革项目（编号：13JGZ19）；成都理工大学优秀创新团队培育计划资助项目（编号：KYTD201301）。