例谈小学数学教学中数形结合思想的渗透

易玲

在小学数学教学中，数与形是两条贯穿始终的主线。数形结合既是重要的数学思想，又是解决数学问题的重要方法。在教学中有意识地向学生渗透数形结合的思想对数学学科的后续学习，乃至学生的终身发展都具有十分重要的意义。本文笔者结合教学实践，谈谈自己的想法。

一、在数的概念教学中渗透数形结合思想

数的概念教学是小学数学教学中的重要内容，是形成数学知识体系的基础。然而对于小学生来说，数学概念是抽象的，因此，教师应充分利用图形，将图形的形象与概念的抽象建立联系，用恰当的图形演示数学概念中最本质的属性，丰富学生的感性材料，从而为学生建构数学概念奠定基础。在课堂教学中，通过数与形的不断转化，引领学生经历概念的形成、概念的理解及概念的应用三个阶段，使得学生对于概念由感性的表象发展到理性的概括理解。

如在“分数的初步认识”一课的教学中，可借用多种图形材料去帮助学生认识分数，初步感悟分数的含义。首先教师在创设情境中让学生创设符号来表示“一半”，有图形语言，有文字语言，有符号语言，如、、等，在对比与交流中不仅要让学生体会符号语言表示的优越性，同时也要能借助图形语言去引导学生初步认识分数。

其次，在揭示分数概念之后，引用历史材料等图形史实，展示各个不同年代分数的表示方法，让学生感受分数的产生、发展过程，更重要的依然是用充分的“形”去理解分数的含义。

比如分数，古代的中国人、埃及人以及阿拉伯人表示的方式都各有不同。

古代中国人算筹表示法    古代埃及人表示法     阿拉伯人表示法

直到印度人发明了“—”，就成为了我们现在所通用的表现形式了。

最后采用线型模型丰富学生的认识表象，设计在数轴中寻找分数位置的联系。除了用以巩固学生对分数含义的理解外，还为学生全面理解分数的含义提供多种直观支持，将分数与整数的关系建立起整体表象，帮助学生建构与完善知识体系。

在小学阶段的数学学习中，有诸多关于数的概念的内容，如小数、百分数等，教师要充分挖掘、利用图形的特质，让“形”成为教师教学的得力助手，用“形”去阐述“数”的知识本质，沟通数学知识之间的内在联系;也让“形”成为学生思维发展的“脚手架”，促进学生对概念的认知从具体形象的层面向理性感知的层面过渡。

二、在数的运算教学中融合数形结合思想

在计算教学中，引导学生关注算法背后的算理，实现算理与算法的交融是教师教学的重要关注点。教师要有意识地在数的运算教学中融合数形结合思想，用看得见、摸得着的实物，直观形象地演示算理，帮助学生以形促思，以形助数，从而实现由算理到算法的过渡。

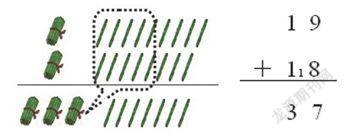
如在“两位数加两位数进位加法”一课的教学中，教师引导学生先用小棒摆一摆、算一算19+18，再结合小棒图，引导学生一步步说出竖式计算的过程，用摆小棒与列竖式并行的方式去演绎“满十进一”的算理。

在这里，直观操作是为了解决学生计算中遇到的障碍，体现了以“形”助“数”的必要。在直观操作的基础上让学生抽象出竖式计算的过程。而在之后的教学中，教师没有把直观图丢到一边，而是引导学生反思整个过程，寻找竖式计算的每一步与直观图中的哪一部分有联系，了解直观图与竖式计算的内在关系。因为竖式计算的每一步都有直观图的支撑，所以学生能形象地理解“满十进一”的算理，实现算理与算法的交融。

又如在分数乘、除法的一系列教学中，教师始终可以用长方形纸片作为素材，让学生通过“分一分、涂一涂”的操作，将“数”的问题转化为对“形”的分析，从而借助图形语言理解分数乘、除法的算理。因此，将数形结合的思想融合到运算教学中，能有效寻找数与形的联系，充分揭示计算方法的本质，为沟通算理和算法服务。

三、在解决问题教学中运用数形结合思想

（一）用“数形结合”化复杂为简单，理清数量关系

数量关系是数学所特有的研究对象，《义务教育数学课程标准（2011年版）》明确提出要“从现实生活或具体情境中抽象出数量关系”。在一些解决问题教学中，数量关系是教学的重点、难点，因其数量关系多且繁，学生掌握起来十分困难。如果充分运用数形结合思想，巧妙运用线段图等恰当的图形直观地表示其数量关系，常能产生意想不到的效果。

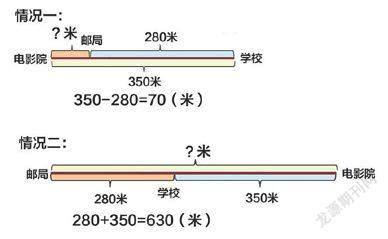
如解决“邮局、电影院和学校在创业大道的同一边。邮局距学校280米，电影院距学校350米。邮局距电影院多少米？”这一问题时，大部分学生只有一种答案，280+350=630（米）。教师如果能引导学生用画线段图的方式表达题意，学生就会有疑惑：邮局、电影院和学校应该在什么位置呢？用线段图就能清楚、直观地表示出两种不同的情况（如下图）。

直观的线段图不仅可以吸引学生的兴趣，更重要的是可以帮助他们在适当的图形中让复杂问题简单化，抽象问题形象化，利于学生抽象出数量关系，建构基本的数学模型，有效提高解决问题的效率。

（二）用“数形结合”化抽象为直观，巧妙解决问题

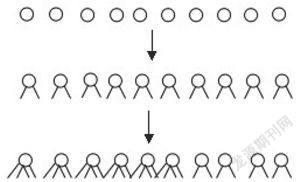
如鸡兔同笼问题——已知鸡和兔一共有10只，一共有32条腿，求鸡兔各有几只？这类题目的解决方法很多：（1）列方程解答，（2）枚举法，（3）假设法。但是，对于小学生而言很多方法受到了限制，比如中低年级学生不会用方程，无序的枚举容易导致枚举不全面，假设法的数量关系很抽象，学生难以理解。用什么样的方法让低年级的学生也可以解决这个古老的难题呢？其实充分运用“数形结合”就能巧妙地解决这个问题。用圆表示10只动物。假设全是鸡，则每只鸡有两条腿，把腿画出来，只有20条腿，但还有32-20=12条腿没画。如果每只再添2条腿，这样还得添12÷2=6只，得出兔子有6只，鸡有4只。

在类似的教学中，都可以让学生画直观图的形式，通过借助直观图这种“数形结合”的方式来使得看似抽象的问题直观化，这显然更符合小学生以具体思维为主，并逐步向抽象思维过渡的思维特点，从而让解决问题变得轻松自如，且保护了学生的学习信心，激发学习兴趣。

总之，在小学数学教学中，教师应有意识地强调和渗透数形结合的思想和策略，以“形”的直观表达“数”，以“数”的精确研究“形”，将抽象变具体，把无形变有形，实现教学的有效突破，从而更好地促进学生的数学学习。

（湖北省武昌水果湖第二小学   430071）