“把所有的都包起来”

孙佳威 付春红

《义务教育数学课程标准（2011版）》提出了“模型思想”这一概念。什么是模型思想？课标中虽然正式提出了模型思想的基本理念和作用，明确了模型思想的重要意义，但是对于教师来说，要想真正把模型思想融入课堂，帮助学生在数学课堂中建立起“数学模型”，却不是一件容易的事情。甚至有许多一线教师认为，在课堂中实施了“问题情境—建立模型—解释、应用与扩展”的模式就是在帮助学生建立模型，而这显然是一种形式主义。那么究竟该如何帮助学生建立模型思想呢？观摩了吴正宪老师的一节数学课，对我们颇有启发。

吴老师的教学内容是人教版四年级上册的“商的变化规律”一课。面对这样一个被大家研究“透”的教学内容，我们最大的疑问就是：吴老师还能怎样上出彩？面对新课标，她的着眼点在哪？

上课伊始，吴老师像以往教学“商的变化规律”一课一样，以“猴王分桃子”的情境，引导学生列出了三个算式：6÷2=3、60÷20=3、600÷200=3进行研究。面对这个熟悉的情境，我们的热情一下降到了冰点，正当我们失望时，吴老师后面环节内容的处理，给了我们一个又一个的惊喜。

惊喜一：借助直观，浅悟模型

当学生对于“猴王分桃子”的三个算式有了初步的感悟后，吴老师没有引导学生继续纠结于几个算式呈现的规律的研究，而是以几何直观的形式帮助学生继续感悟规律：

师：孩子们，这其中的规律是什么呢？我们再来看一组题。

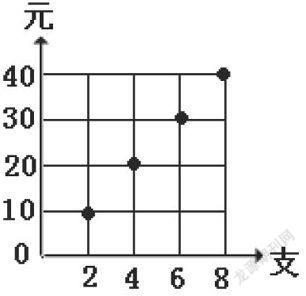
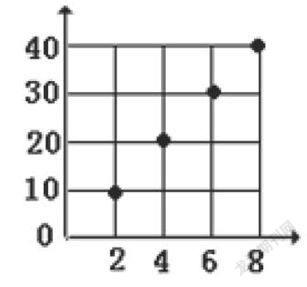
（出示图）：

师：你看到了什么？

生：我看到横着的是表示有多少支笔，竖着的是表示多少元。

师：你知道它们之间有什么关系吗？

生：买两支笔就是10元，买4支笔就是20元，买6支笔就是30元，买8支笔就是40元。

（随着学生说在图上点出点来。）

师：想一想，买10支笔的点应该去哪了？

生：在直的线上再往上。

师：你有什么新的发现吗？

生：商都是5。

师：那这个5又是什么呢？

生：一支笔的价钱。

师：你怎么求出来的？

生：我通过总的价格除以笔的支数求出每支笔的价格。

师：笔的数量和总的价格在发生着变化呀。

生：但是都是每支5元钱，不变。

此时老师没有局限于图的理解和学生的表达，而是引导学生用手势一起再次感受。

师：你们的意思是——买的支数越来越多，钱也就越来越多，但是每支笔的价钱是永远不变的。

（吴老师边说边一只手臂伸开代表横轴，另一只手臂伸开代表纵轴，慢慢地延展开手臂，帮助学生逐步地感悟被除数和除数增加的过程，感悟商不变的原因。）

此时，学生对于“商不变”的理解绝不仅仅是抽象的算式，还有直观图形的感悟。正是这样一幅图的引入，就帮助学生把代数问题引入到图形的理解中来，渗透了几何直观思维方式的同时，把商不变的规律与直观模型建立了紧密的联系。

惊喜二：层层感悟，抽象模型

在这样研究的基础上，吴老师引导学生继续研究算式的变化规律。

师：这些算式的商怎么就不变了？请大家选一组为例，把你的发现表示出来。

（学生进行小组研究。）

师：谁来说说你们的研究的过程和发现？

（学生展示自己的研究过程和发现。）

师：你能根据你们的这个发现，再写出几组这样的算式吗？

生1：4÷2=2   40÷20=2

生2：8÷2=4   80÷20=4

生3：20÷5=4   200÷50=4

……

当学生兴趣盎然地举不胜举时，他们心中对于商不变的规律已经有了一定的感受，学生虽然没有说出总结性、规律性的东西，但是商不变的规律大有呼之欲出的态势。此时，吴老师恰如其分地引导：

师：你们说得完吗？

生：永远都说不完，太多了！一辈子也说不完！

师：那问题就来了，一辈子也说不完。（教师用一个……表示出来）就这个一辈子也说不完的事，你们能不能总结一下，用一句话或者一个式子来表示。你想到什么，就写什么。

（学生自己静下心来反思学习过程，尝试写出自己的感悟。）

师：展示一下你们的想法。

生1：我发现怎么也写不完，永远也写不完。

生2：商与被除数、除数有关系。

师：你们想问他点什么？

众生齐问：到底有什么关系？

生2：我发现它乘2、它也乘2，商就不变。（结合着一个算式说。）

生3：你乘10、我乘10，商就不变。

生4：你乘几，我乘几，商就不变。

师：这个你是谁？我是谁？商才不变呢？

生4：你就是被除数，我就是除数。

师：看她就把前边你们所表达的意思总结出来了。3号同学，你面对他的总结有什么要说的吗？

生3：我没有把所有都说全，还有的不是乘10呢，她就把所有的都说全了。在总结的时候，要把所有的情况都包起来。

师：对呀，要把所有的说全了，刚才有些同学的帽子有点小了。

师：我看到有的人还是这样总结的（如下图），你有什么想法吗？

生：我觉得还可以把方框变成x 。

师：你的x代表什么？

生：要是5就都是5，要是10就都是10。

在这个环节中，吴老师技巧性地、分层次地让学生展示自己的想法，学生的想法逐步地由初步感知的“永远也写不完”到“你乘几我也乘几、商不变的表达”，最后用“x”这个简洁符号来表示，不仅体现了学生由粗略体验到细致分析、由形象感知到抽象归纳的过程，更重要的是他们体验了一把建立模型的过程，正如生3在自我反思的过程中所说的：“要把所有的都包起来。”是呀，有了充分的体验、层层的感知，学生的总结中终于提到了“要把所有的都包起来”，这个“把所有的都包起来”的符号表达就是帮助学生建立的抽象模型。

惊喜三：回顾过程，应用模型

如果说前面的学习过程是学生在教师引导下的一种抽象概括，那么怎样让学生在以后的学习中也能够有所发现，也能尝试用简洁的方法来表达自己的发现，是这节课的一个重要的研究点，也是帮助学生积累活动经验的过程。于是吴老师引领大家回顾了整个学习过程。

师：我们来回头看看，是怎样总结出这个规律的。

大屏幕显示画面和过程：分桃子→买笔图的观察→自己写式子→回到生活中验证。

师：看这个图，我们把单位“元”和“支”去掉，你还能根据它编一个小故事吗？

生1：我买2块糖用10元钱，买4块糖20元钱……每块糖5元钱的商不变。

生2：我去二姨姥姥家，2秒钟跑10米，4秒钟20米……每秒钟跑5米的商不变。

……

如果说前面的过程是在建立模型的话，那这里吴老师就是在引领学生应用模型，把模型还原到现实生活中去应用。经历这样的过程才算得上是一节完美的建模课。更让人惊喜的是，吴老师模型的应用又再一次和几何直观建立了联系。面对学生的“去二姨姥姥家”的事，我们所有的听课教师都发出了会心的笑声，笑声中既有对吴老师睿智课堂的钦佩，更有对学生成功体验的愉悦。

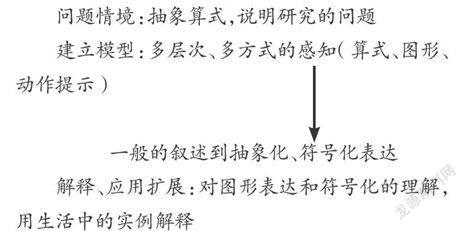
综观吴老师的授课过程，不难发现吴老师在走的其实也是那一条建模之路：

问题情境：抽象算式，说明研究的问题

建立模型：多层次、多方式的感知（算式、图形、动作提示）

一般的叙述到抽象化、符号化表达

解释、应用扩展：对图形表达和符号化的理解，用生活中的实例解释

当我们带着无比艳羡的目光惊叹之余，反思自己的课堂教学，我们也曾严格按照“问题情境—建立模型—解释、应用与扩展”这样的模式在进行摸索，我们的课堂怎么就那么别扭而又索然无味呢？对比之后终于豁然开朗，“建立模型”是引导学生在多层次感知中逐步地完善和抽象，是学生在学习过程中的一种体验的提炼、一种过程的积累。我们的问题归根结底还是出在了认识上、理念上，建立模型不是教师建立，而是学生建立，是教师帮助学生在丰富的感知中进行抽象的提炼。所以教师需要努力做到的仅仅是少一些急于求成、多一些耐心等待;少一些抽象说教、多一些形象感知;少一些包办代替，多一些宽松体验;少一些知识传送，多一些经验积累。相信如此，我们的“建模课堂”也会像吴老师一样不断地给自己、给学生带来“惊喜” ！

（北京市朝阳区教育研究中心  100000

北京市朝阳区望京南湖东园小学  100000）