pi的二阶广义幂指函数表示搜索法

2015-09-09崔雷

哈尔滨师范大学自然科学学报 2015年5期

关键词：表示法二阶高精度

崔雷

(同济大学)

0 引言

Kunth提出了 up－arrow 计数法［1］，随后笔者独立提出广义幂指函数［2］，这两种表示法实质是一样的.

值得指出的是，参考文献［2］里面，广义幂指函数的直观描述和严格定义是一致的，但实际上广义幂指运算有两种可能.

第一种可能:也就是文献［1］里的表示:

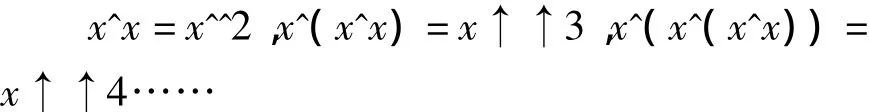
用符号表示的例子为x↑↑3=cma1(x，3，2，py，1).这里面x是底数，3 是指数，2 是阶次，py为前面式子的幂值，1为从原点向正实轴的序号.cma1为广义幂指函数第一种形式.

第二种形式为，也就是文献［2］里面的表示:

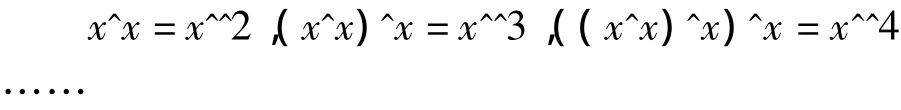
用符号表示例子即为x3=cma2(x，3，2，py，1).此表示法含义同上.

这两种表示法，不同之处在于运算方向，cma1是从右向左计算，cma2是从左向右计算.值得注意的是，两种方法的结果截然不同.

根据这两种描述得到严格定义是容易的，该文不再赘述.

关于二阶广义幂指函数(无论TypeI还是TypeIIT)中，分数指数的假设为:

这种假设，对于一阶幂指函数显然成立:

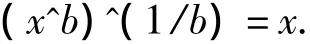
利用假设可以解决求解2560.5问题，值得注意的是:2560.5不等于 2560.5.同时，文献［2］的这个假设，也说明超越数的数量远远大于非超越数.

由于广义幂指函数是超越函数，因此从上述求解过程可以尝试用二阶广义幂指函数来表示pi，形式为(a/b)(c/d)=pi、或者(a/b)↑↑(c/d)=pi.

为了表示pi，有两类思考方法:即直接求解二阶幂指pi值得到表示，和利用参考文献的假设用pi的某个二阶幂指得到有理数然后反向表示.下面分别介绍如下.

1 pi的正向搜索法

pi的正向搜索法，即直接用(a/b)(c/d)或(a/b)↑↑(c/d)遍历搜索，其中a/b从某个比较小的a和b开始一直尝试到比较大的a和b.值得注意的是，应该保证其比值在某个显而易见的范围内.而c/d要特别选取，因为这种搜索通常使用matlab之类软件计算，而目前的问题是这类软件没有计算分数次指数的办法，所以通常c/d选择2、3、4之类的自然数.即最优先的尝试，是计算(a/b)2、(a/b)3依次计算或者(a/b)↑↑2、(a/b)↑↑3依次计算.如:在计算(a/b)2 的时候，因为(1741/938)2=3.1415，所以选择比较接近1741/938的分式进行计算.同样，因为(2003/1267)3=3.1413，所以选择接近2003/1267的分式进行计算.其他类推.

由于计算遍历搜索需要更高精度表示a/b的值和之后的结果，因此该文第4部分提出更高精度的计算机实现方法.

实际上，这一部分给出的是最原始的求解广义幂指函数底数的办法，如果有其他办法，可以忽略本节.

2 pi的逆向搜索法

和正向搜索法不同，逆向搜索法是直接搜索(pi*a/b)(c/d)=k，而遍历a、b、c、d后，寻找k为某个循环小说.因为一旦k为某个循环小数，可以根据文献［2］直接得到pi的二阶广义幂指函数表示.广义幂指函数的Type I类推.

这里，当a、b均为1时，c/d=2时，即计算pipi，可得其值约为4339/119;同样，计算

(pi/2)2值约为1805/888.同样，c/d可以选择2、3、4 之类的自然数.

3 更高精度的计算法

在前述两种搜索方法中，都会用到某个小数的更高精度表示.为此，笔者提出如下解决方案:

由于在定义a、b、c、d的时候使用的是计算机表示的实数，而a/b结果为双精度浮点数，其精度不能满足要求.为此，可以使用数组的办法解决.即定义某个字符数组h1、h2，其含有小数点.对于h1和h2的乘除运算，采用类似于手算的办法，即h1的各个元素，和h2的各个元素，分别对应运算.这样，就把对应运算控制在比较小的、精确的范围内.由于这种运算是乘除法，因此得到结果可用某个数组h3表示，而h3的长度是可调的.这样，就完成了任意长度实数之间乘除(也包括加减)运算得到任意精度实数的计算机实现.

现在的问题关键是二阶幂指运算，其可以表示为有限次的代数运算模拟.而本节实现了更高精度的表示问题，这样，可以利用类似手算的办法，解决二阶幂指运算.

对于逆向搜索，在得到精度可调的k值之后，利用逻辑查找循环字节.这个应该是容易实现的.