随机变量数学期望计算*

陈红燕，邓 臻

(青岛工学院)

1 离散型随机变量数学期望的计算

离散型随机变量X的概率分布为P{X=xk}=pk，k=1，2，…，如果级数绝对收敛，则X的数学期望

例1 随机变量X的分布律为P{Y=0}=p，P{Y=1}=1－p，其中0＜p＜1，则X的数学期望利用公式(1)易得E(X)=p.

对于一般离散型随机变量其数学期望均可由上述公式得到，也有一些随机变量需要结合随机变量间的关系及性质转化得到.

例2 随机变量X服从参数为n，p的二项分布，其中n为正整数，0＜p＜1，分布律为P{Y=显然直接用公式(1)求期望，计算困难.但结合二项分布与两点分布的关系，随机变量X可分解为n个两点分布变量的和，即X=X1+…+Xn，故E(X)=np［2］.

2 连续型随机变量数学期望的计算

设X是连续型随机变量，其概率密度函数为f(x)，如果积分绝对收敛，随机变量X的数学期望

一般连续型随机变量运用积分公式均可求得数学期望，只是个别积分计算需要结合微积分中的一些特殊积分方法.

3 混合型随机变量数学期望的计算

取值既包括离散的点又含有区间的这种非离散型非连续型随机变量称为混合型随机变量，下面来探讨关于这一类型随机变量数学期望的计算问题.

例3 随机变量X的取值为区间［－1，2］，，在事件{－1＜X＜2}的条件下，X在区间(－1，2)内的任一子区间上取值的条件概率与该子区间的长度成正比.很明显，随机变量X为混合型随机变量，下面计算它的数学期望.

其实随机变量X可以看成由离散型随机变量与连续型随机变量两个部分组成，其中的连续型部分又可看成是占有整个取值范围概率的均匀分布，结合一般随机变量数学期望的计算:

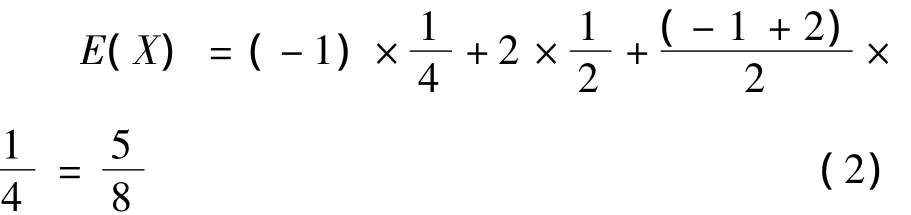
在上例中，如果设随机变量X的分布函数为FX(x)，经过分析容易得到

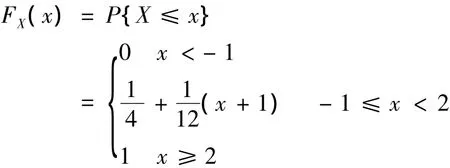
根据分布函数的性质，因此(2)式离散型部分又可写为(－1)×ΔFX(－1)+2×ΔFX(2)，其中ΔFX(x)为FX(x)在x点的跳跃;连续型部分，由区间(－1，2)为分布函数FX(x)可导的区间，，所得结果与上述结果完全一致，因此可以得到混合型随机变量的数学期望的一个一般化方法.

设随机变量X的分布函数为FX(x)，根据分布函数的性质FX(x)为单调不减的有限函数，其至多有可列个跳跃间断点，可设x1，x2，…，xi，…为其间断点，I1，I2，…，Ii，… 为其可导区间，则随机变量X的数学期望为:

上述公式为一个一般化公式，很多随机变量取值并没有那么复杂，故其数学期望的计算也相应可以简化［3］.

例4 设随机变量X与Y相互独立，X服从参数为μ，σ2的正态分布，Y为两点分布，分布律为，求Z的数学期望.

解 随机变量Z的分布函数记为FZ(z)，X的分布函数记为FX(x)由题意可得

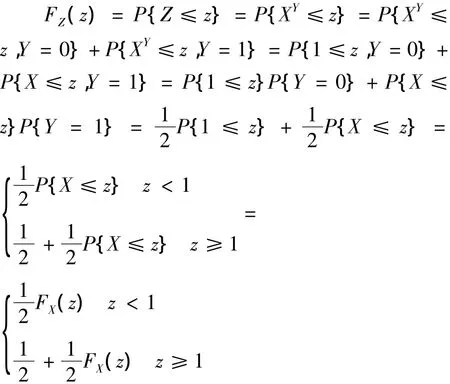
(由于X为连续型随机变量，X=0对本题的影响可忽略不计)，根据混合型随机变量数学期望求解公式(3)得

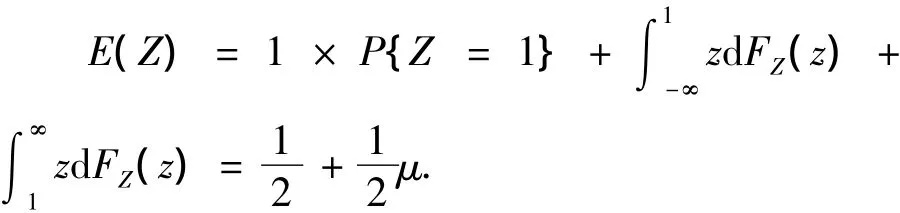
4 结论推广

设(S，，P)为样本空间，X是此空间上的随机变量，其分布函数记为FX(x)，对任何(R，B(R))上的可测函数h(x)，h(X)是(S，，p)的可测函数，则(只要式子一端有意义即成立，可见参考文献［4］).

［1］陈红燕，郑素华，邓臻.概率论与数理统计［M］.青岛:中国海洋大学出版社，2013.

［2］盛骤，谢式千，潘承毅.概率论与数理统计:4版［M］.北京:高等教育出版社，2008.

［3］何晓霞，侯萱，李春丽.混合型随机变量期望的求法及应用［J］.大学数学，2014，30(1):101–103.

［4］程士宏.测度论与概率论基础［M］.北京:北京大学出版社，2004.