二维抛物型偏微分方程初边值问题的解法分析

张正林

(宿州学院)

0 引言

从牛顿时代起，物理问题的研究就成为数学发展的一个重要源泉.18世纪数学和物理的结合点主要是常微分方程，对于偏微分方程也进行了初步的研究，如弦振动方程、波动方程、位势方程.随着物理科学所研究的现象从力学向电学以及电磁学扩展，到了19世纪，偏微分方程的求解成为数学家和物理学家关注的重心，如1882年，基尔霍夫(德，1824—1887年)完成了3维波动方程的求解.傅里叶应用三角级数求解热传导方程，同时为了处理无穷区域的热传导问题又导出了“傅里叶积分”，极大地推动了偏微分方程边值问题的研究.此外，他是傅里叶定律的创始人，在代表作《热的解析理论》中解决了热在非均匀加热的固体中分布传播问题，成为分析学在物理中应用的最早例证之一，对19世纪的理论物理学的发展产生深远影响.该文研究抛物型方程的有限差分方法，从二维常系数线性抛物型方程的差分方法进行讨论，给出几种典型的差分格式并讨论其稳定性与收敛性等性质，对变系数以及多维抛物型方程也进行了研究.

1 二维抛物型偏微分方程概述

在研究热传导过程、气体膨胀过程和电磁场的传播等问题时，常常遇到抛物型偏微分方程.这类问题的自变量中，有一个是实际问题中的时间变量，常用t表示.所以抛物方程通常描述的是随时间变化的物理过程，即所谓不定常的物理过程.抛物方程的定解问题有三类，即纯初值问题、半无界域上的初边值问题和有界域上的初边值问题.

偏微分方程按是否与时间有关可分成两类.讨论的椭圆型方程通常用于描述不随时间t变化的稳态物理现象，如温度、电位等，这类问题称为驻定问题.而抛物型方程和双曲型方程用于描述随时间t变化的非定常物理现象，这类问题称为非驻定问题.驻定问题可看成非驻定问题当t→∞时的渐近状态.在研究偏微分方程的数值解法时，注意这两类问题的区别和联系是有益的.

2 二维抛物型偏微分方程初边值问题分析

考虑如下二维抛物方程的差分格式.

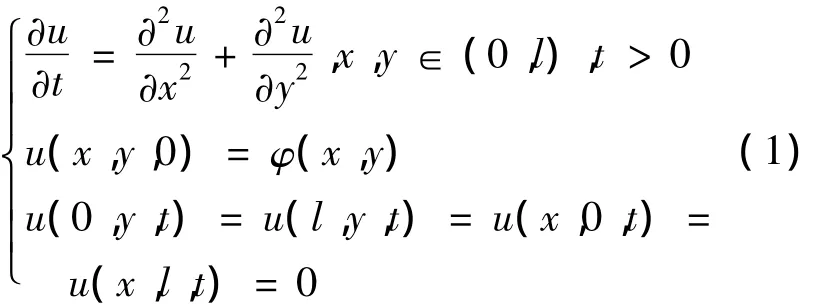
取空间步长h=l/N，时间步长τ＞0.作两族平行与坐标轴的网线x=xj=jh，y=yk=kh，其中j，k=0，1，…，N，将矩形区域(0，l)×(0，l)分割成N2个小矩形.记unjk为网格节点(xj，yk，tn)上的差分解.

前述各种一维差分格式都可以直接用于以(3a)、(3b)为代表的二维以至更高维的抛物方程.例如，向前差分格式成为

实际计算时，先令n=0，利用已知的φ(xj，yk)等，对j，k=1，…，N–1，用(2)算出u1jk.而由边值条件，补充得到0.下一步，令n=1，利用已知的第1层的差分解{u1jk}类似地算出第2层的差分解{u1jk}.以此类推，直到

3 二维抛物型偏微分方程初边值问题的解法

用六点对称差分格式，ADI法，预校法和LOD法求解二维抛物型方程的初边值问题:

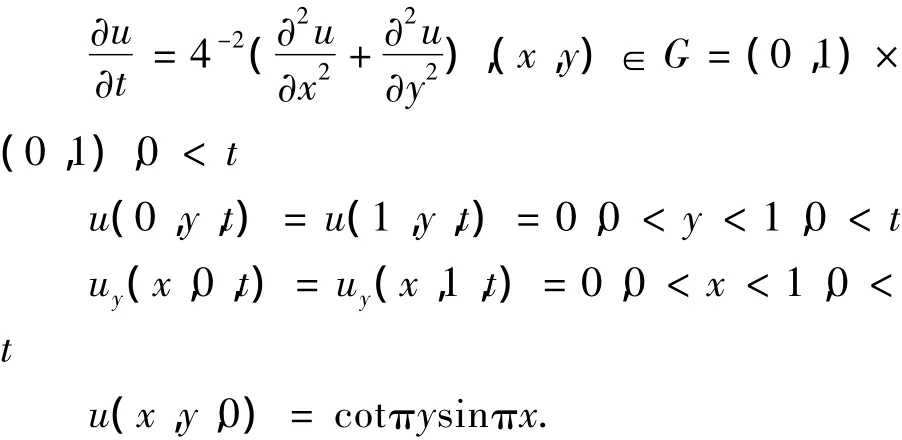
设xj=jh(j=0，1，…，J)，yk=kh(k=0，1，…，K)，tn=nt(n=0，1，…，N)，差分解为，则边值条件为

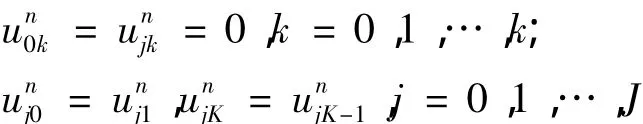
下面给出的求解二维抛物方程的LOD格式(局部一维格式)就是其中一例.

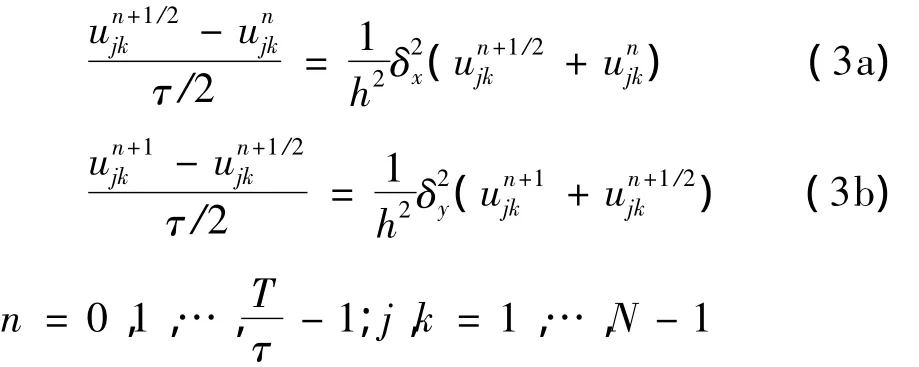
其中

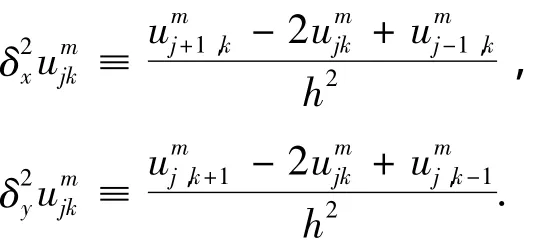
LOD格式的计算步骤可以总结如下:

(1)令n=0，k=1.

(3)若k＜N，则k增加1，转步骤(4).否则转(4).

(4)令j=1.

(6)若j＜N，则j增加1，转步骤(5).否则转(7).

(7)若n＜T/τ，则n增加1，转步骤(2).否则结束.

若时间方向用向前差商，空间方向用线性有限元，并记fk=f(x，kτ)，则有限元方程为:对k=1，…，K=T/τ，逐层求Vh满足

这相当于在每一层要解一个线性方程组:

或者稍微整理一下:

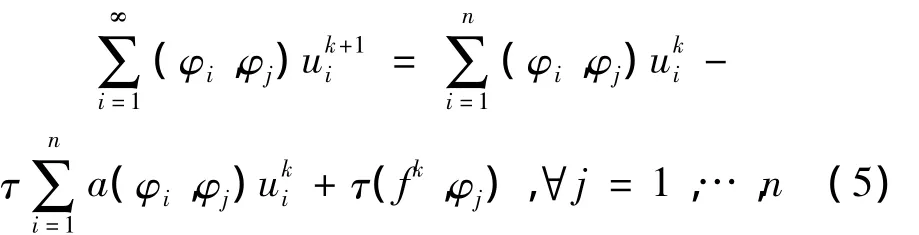
如果在时间方向用梯形公式，则类似于(3a)(3b)得到所谓Crank－Nicolson格式:

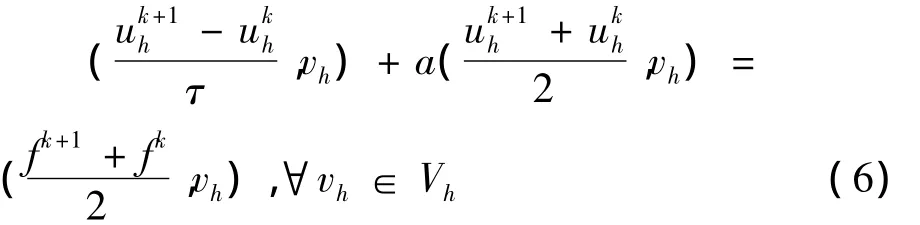
4 结束语

相容性是二维抛物型偏微分方程差分方法中一个非常基本的概念，它对差分格式的收敛性会有影响，一般来说，要用差分格式求解二维抛物型偏微分方程问题，相容性条件必须满足，可以看出，建立的差分格式都是相容的差分格式.

［1］于勇.抛物化Navier－Stokes方程(PNS)和高氏PNS理论及其应用的评述(英文)［J］.空气动力学学报，2015(1):54－65.

［2］范乐乐，钟华.一类非线性延迟抛物偏微分方程的紧致差分格式［J］.数学的实践与认识，2015(3):206－213.

［3］汪维刚，许永红，石兰芳，等.一类双参数非线性高阶反应扩散方程的摄动解法［J］.应用数学和力学，2014(12):1383－1391.

［4］王菲菲，王宁.带有加权源与吸收非线性质的抛物型方程的爆破时间的界及爆破速率的估计［J］.南开大学学报:自然科学版，2014(5):26－30.

［5］崔雷，姜恒志，陈晓亮，等.曲线坐标下波浪抛物型缓坡方程及近岸流数值模型研究［J］.应用基础与工程科学学报，2014(6):1204－1216.

［6］艾岭.基于小波基的非线性抛物型系统模型预测控制［J］.电机与控制学报，2015(1):90－95.

［7］范飞，徐文琦，梁丙臣.Boussinesq方程与抛物型缓坡方程2种波浪模型的比较分析［J］.中国海洋大学学报:自然科学版，2014(2):102–105，111.

［8］Liao Honglin，Sun Zhizhong.Maximum norm error estimates of efficient difference schemes for second－order wave equations［J］.Journal of Computational and Applied Mathematics，2010(8).

［9］Zhang Chengjian.Nonlinear stability of Runge－ Kutta methods applied to infinite－ delay－ differential equations［J］.Mathematical and Computer Modelling，2013(4).

［10］Zhang Chengjian.Stefan Vandewalle.Stability analysis of Volterra delay－integro－differential equations and their backward differentiation time discretization［J］.Journal of Computational and Applied Mathematics，2012(8).