开尔文源格林函数数值计算方法对比研究

姚朝帮，董文才

(海军工程大学舰船工程系，湖北武汉430033)

开尔文源格林函数近年来得到了较为广泛的应用［1-4］，它由Havelock在1928年导出，现在被称为Kelvin(或Havelock)源，其物理意义是以恒定速度直航的单位点源在场点所产生的速度势，表示为双积分形式，被积函数具有奇异性、振荡性，直接采用数值积分计算很难保证计算精度与效率，也难以应用到船舶水动力问题的计算。为此，很多学者将其变换为易于计算的形式，常见的有Peters型，Michell型和Havelock型，Noblesse归纳了这3种形式的推导过程［5］。不同表达形式有所不同，本文选用的是Havelock型的改进形，即将Kelvin源格林函数表达成Rankine源及其关于静水面的映像源项、近场扰动项N和远场波动项W。Rankine源及其关于静水面的映像源项可采用Hess-Smith提出的方法计算。因此，本文重点讨论扰动项N和远场波动项W的计算方法对比分析。

近场扰动项N的计算方法主要有4种:1)制表法［6-8］，通过直接数值积分，形成关于扰动项N及其偏导数的大规模数据。该方法的优点在于制表与船型本身无关，制表一旦形成，可以用于不同船型兴波流场的计算，但为了提高计算的精度，通常需要规模较大的制表，通常可达到expt;2)切比雪夫多项式拟合法［9］，采用切比雪夫多项式对N进行拟合计算。采用该方法时，N的计算精度能达到5D-6D，但偏导数的精度会有所降低;3)有理函数法，将格林函数双积分形式变换成只包含有理函数的单积分形式［10-11］，在此基础上采用梯形法或辛普森方法计算积分。但实际计算时需要权衡积分精度与效率;4)使用多项式对N进行拟合［12］，从而简化计算，但该方法的精度及有效性还有待进一步验证。

远场波动项W的计算方法主要有3种:1)Bessel函数法，通过引入Dawson型积分将W转化为Bessel函数的表达形式［13-15］，利用Bessel函数的相关性质进行计算。采用该方法时需要分区进行求解，在区域过渡的地方，计算结果有时会出现跳跃;2)有理函数法，与求解N项时的方法相同;3)变量代换法，对W的单积分形式进行变形，利用变量代换得到易于积分的形式。

上述N与W的计算方法各有特点，也被广泛采用，但公开发表的文献很少涉及它们计算精度、效率的对比及优选，基于此，本文对上述常用的方法进行总结分析，并评估它们的精度、效率，从而找到该格林函数的快速数值计算方法，为将该格林函数应用于船舶水动力的计算奠定基础。

1 Kelvin源格林函数

设移动源的前进速度为U，ξ=(ξ，η，ζ)为源点，X=(X，Y，Z)为场点，L为特征长度，g为重力加速度，采用L、g及U对相关参量进行无因次化，x=X/L，F=，则Kelvin源格林函数的表达式为［8］

G*对场点的偏导数的表达式可参见文献［8］，其和G*的计算相比并未引入计算难度。

2 近场扰动项N(a)的计算方法

2.1 制表法

制表法是通过直接积分计算N(a)，进而得到大规模的N随(a1，a2，a3)的变化规律，并以此作为插值数据库。

数值积分计算时，对式(2)中N(a)的表达式进一步变形，得到在t∈［-1，1］时比积函数更为光顺且积分端点处奇异性消失的N(a)及∇aN(a)表达式［8］:

制表时需将a1、a2、a3、d投射到［0，1］区间内，因此定义如下变换:

为了方便插值计算，采用式(9)对N(a)及∇aN(a)进行变换:

本文选取的制表规模为193×45×28。式(3)～(6)的积分计算采用自适应辛普森法。

2.2 切比雪夫多项式拟合方法

Newman从开尔文源格林函数双积分形式出发，得到了Kelvin源格林函数近场项的切比雪夫多项式拟合形式，并计算得到了拟合系数［9］。该方法N的计算式为

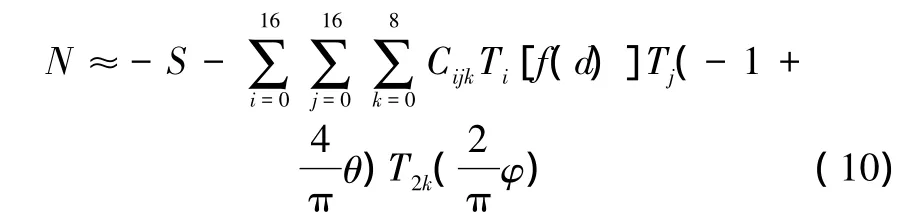
式中:f(d)==arcsin(a1/d)，

φ=arctan(a2/a3);Ti，Tj，T2k是切比雪夫多项式，文献［15］给出了具体的迭代求解方法。S由式 (11)计算得到:

Vm、Um可分别通过式(12)、(13)求解:

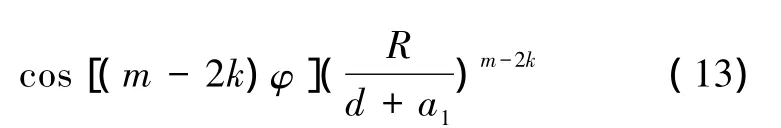
式中:初值U0=

式中，s=

采用该方法计算Kelvin源格林函数时，N、W与其他计算方法的对应关系为

采用自适应辛普森法计算式(14)中的积分，可同时得到N及W。

2.3 有理函数法

Wang［10］等在Bessho得到的开尔文源格林函数表达的基础上，进一步整理分析，得到了开尔文源格林函数的有理函数表达形式为

2.4 改进的梯形法

图1 改进梯形法流程Fig.1 Solution strategy for improved trapezoidal rule

分析式(4)～(7)可以看出N(a)及其偏导数只是在积分端点附近变化比较剧烈，其他区间的曲线较为平滑，有利于直接积分。借鉴自适应梯形法和自适应辛普森法的思想，根据被积函数的特性，将被积函数的积分区间分为［-1，-1+Δh］，［-1+Δh，1-Δh］和［1-Δh，1］，Δh为积分端点处的微元段。在区间［-1，-1+Δh］及［1-Δh，1］采用局部加密的方法进行离散，并利用梯形法求得积分值，文中将这种方法称之为“改进的梯形法”，其基本流程见图1。

3 远场波动项W(a)的计算方法

3.1 Bessel函数法

Bessho通过引入Dawson型积分，将开尔文源格林函数的波动项转换成了Bessel函数的级数形式［13］为

式中:Jn、Kn、Yn、Ⅰn为Bessel函数，J'2n、Y'2n为关于a1的偏导数。

对式(16)关于a1、a2、a3求偏导便可得到对应的导数项;求和项数由指定的计算精度确定。

3.2 变量代换法

由式(2)可知W(a)及其偏导数的表达式为

W(a)是振荡的，振荡的频率与a1、a2有关，振荡的幅值与a3有关，对于这类积分，若按常规的方法进行积分，积分效率较低且很难得到正确的结果［16］，本文提出变量代换的方法来处理，以期能同时兼顾积分效率与精度。

设W(a)的实际积分区间为［tg，th］，令 τ=，则W(a)的被积函数在［tg，th］的积分可化为

式(19)是一个复函数和指数函数的积分，设该复函数为f，则f=(l-im)/(l2+m2)。

设［tg，th］离散后的序列为t1、t2、t3、…、tn，对应的A序列为A(t1)、A(t2)、A(t3)、…、A(tn)，可将f在相邻两点A(ti)和A(ti+1)(1≤i≤n-1)间的函数用关于A(ti)的一次函数近似，那么被积函数在相邻两点间的积分Ⅰi可直接积出，整个积分区间的积分值为各Ⅰi的和:

经过上述变量代换后，将振荡函数转换成了易于积分的表达形式，积分精度取决于f本身的函数特性及其所对应的离散方法。为此，开展其函数的性状分析，并重点分析m=0的邻域内的变化情况。图2给出了f在积分区间内的2种典型函数曲线(图中框点为m=0对应的点)。从图中可以看出，在m=0对应的t附近，f函数值变化剧烈，出现了一些看似奇异的现象，但函数本身是连续的，这只是函数f局部区域变化剧烈的“伪奇异”，称之为“伪奇异现象”，与之对应的点称之为“伪奇异点”。

图2 f的典型特性曲线Fig.2 Typical characteristics of f

为了保证积分的精度和效率，在对积分区间进行离散时必须将这种“伪奇异性”考虑进来。区间离散时需要在这些“伪奇异点”处局部加密处理。进一步分析可知“伪奇异点”出现的位置可由式(21)所示的解析形式得到:

需要指出的是，式(18)及(19)中N(a)的积分区间是(-∞，+∞)，不利于数值积分的实施，实际数值计算过程中需要对积分区间进行适当截断，具体截断的方法可参见文献［17］。

4 数值计算结果及分析

为了比较各种计算方法的精度，本文选用如图3所示的算例，算例中点源坐标为(0.0，0.0，-1.0)，并以速度2 m/s沿ox轴正方向运动，场点位于水平面上与ox轴成角度ф=arctan(0.5)的直线上。

评估各种计算方法的效率时仍选用上述算例，此时改变源点的垂向坐标，使其逐渐接近自由表面(Z=0)，计算时源点的垂向坐标分别为Z=-1，-0.1，-0.01，-0.001，统计分析计算一次格林函数及其偏导数需要的平均时间。

图3 移动源点与场点的位置Fig.3 The location of translating source and field points

4.1 N(a)计算结果分析及效率评估

图4中给出了源点位于(0，0，-1)时不同方法计算的N(a)及偏导数的对比曲线。表1中给出了计算一次N(a)及其偏导数的总耗时，其中M1、M2、M3、M4分别代表切比雪夫多项式拟合方法、制表法、有理函数法及改进的梯形法。文中耗时统计均在一CPU为Intel Core i3(频率为2.27 GHz)的PC机上进行。

图4 N(a)及其偏导数的函数图像Fig.4 Images of N(a)and its derivatives

表1 N(a)计算耗时对比Table 1 Computation time comparison of N(a)

从图4中可以看出，不同方法计算的N(a)及其偏导数值基本相同，这说明几种方法的计算精度一致，从而互相验证了方法的有效性。从表1耗时对比可以看出，采用Newman导出的切比雪夫多项式拟合法及制表法效率较高，改进的梯形法次之，采用有理函数法计算耗时较长，主要原因在于3个偏导数计算公式繁琐，求解较费时。

4.2 W(a)计算结果分析及效率评估

仍采用上述算例，采用Bessel函数法、变量代换法及有理函数法分别计算W(a)，统计各种计算方法的耗时与计算精度。不同方法计算得到W(a)及其偏导数的对比曲线如图5所示。表2中给出了各种计算方法计算一次W(a)及其偏导数的平均耗时，表中M4、M5、M6分别代表Bessel函数法，变量代换法及有理函数法。由图5及表2可见:3种方法的计算精度基本相同，变量代换方法的效率明显优于其他2种方法。

表2 W(a)计算耗时对比Table 2 Computation time comparison of W(a)

图5 W及其偏导数的函数图像Fig.5 Images of W and its derivatives

4.3 G*的计算结果及验证

图6 G*及其偏导数的函数图像Fig.6 Images of G*and its derivatives

从4.1 节、4.2 节的对比可以看出:N(a)的计算采用切比雪夫多项式拟合法和制表法效率较高;W(a)的计算采用“变量代换法”效率较高，因此本节将综合采用切比雪夫多项式拟合法与“变量代换法”计算G*。仍采用上述算例，计算得到的G*及其偏导数与文献［18］的对比如图6所示。

从图6中可以看出本节选用的近场项及波动项的计算方法计算G*及偏导数的精度与文献［18］基本相同，计算一次的平均耗时约为6～9 ms，能满足船舶兴波流场计算的工程需要。

5 结论

本文在分析开尔文源格林函数近场扰动项和远场波动项计算方法的基础上，对比分析了各种计算方法的计算精度与效率，通过研究得到以下结论:

1)在研究的场点、源点位置范围内，4种方法计算近场项N(a)及其偏导数的精度基本相同，但效率各异，其中切比雪夫多项式拟合法和制表插值法计算效率较高，在实际计算中可优先选择;“改进的梯形法”在保证精度的同时效率稍低;有理函数法因偏导数表达式较复杂、计算效率降低，实际使用时不建议采用。

2)对比分析了波动项N(a)的3种计算方法，它们的计算精度基本相当，“变量代换法”效率较高，采用Bessel函数级数展开的计算方法次之，Bessho型表达计算耗时较长。

3)综合采用切比雪夫多项式拟合法计算N(a)与变量代换法计算W(a)，能快速得到开尔文源格林函数的计算得结果(一次计算的平均耗时约为6～9 ms)，可作为船舶水动力求解的基本工具。

［1］李子如，陈克强.用面元法预报船舶的兴波阻力及波型［J］.武汉理工大学学报，2006，30(6):1094-1097.LI Ziru，CHEN Keqiang.Panel method for the prediction of ship wave resistance and wave pattern［J］.Journal of Wuhan University of Technology，2006，30(6):1094-1097.

［2］田超，吴有生.水线源强消弃法在船舶定常兴波计算中的应用［J］.船舶力学，2008，12(1):37-45.TIAN Chao，WU Yousheng.Application of the waterline source strength elimination method in the computation of the steady ship waves［J］.Journal of Ship Mechanics，2008，12(1):37-45.

［3］NOBLESSE F，DELHOMMEAU G，YANG C.Practical evaluation of steady flow due to a free-surface pressure patch［J］.Journal of Ship Research，2009，53(3):137-150.

［4］韩端锋，黄德波.近水面潜体兴波阻力的数值预报和收敛性分析［J］.船舶力学，2005，9(1):29-35.HAN Duanfeng，HUANG Debo.Numerical prediction and convergence analysis of wave resistance for submerged body near free surface［J］.Journal of Ship Mechanics，2005，9(1):29-35.

［5］NOBLESSE F.Alternative integral representations for the Green function of the theory of ship wave resistance［J］.Journal of Engineering Mathematics，1981，15(4):241-265.

［6］NOBLESSE F.The fundamental solution in the theory of steady motion of a ship［J］.Journal of Ship Research，1977，21(2):82-88.

［7］PONIZY B，BA M，GUILBAUD M，et al.Fast computation of the Green function for steady ship wave resistance［J］.Transactions on Modeling and Simulation，1993，6:89-96.

［8］PONIZY B，NOBLESSE F，BA M，et al.Numerical evaluation of free-surface Green functions［J］.Journal of Ship Research，1994，38(3):193-202.

［9］NEWMAN J N.Evaluation of the wave-resistance Green function:Part 1-The double integral［J］.Journal of Ship Research，1987，31(2):79-90.

［10］WANG H T，ROGERS J C W.Numerical evaluation of the complete wave-resistance Green’s function using Bessho’s approach［C］//Proceedings of the Fifth Conference on Numerical Ship Hydrodynamics.Washington，DC，USA，1990:133-144.

［11］URSELL F.Mathematical note on the fundamental solution(Kelvin source)in ship hydrodynamics［J］.Journal of Applied Mathematics，1984，32:335-351.

［12］NOBLESSE F，DELHOMMEAU G，HUANG Fuxin，et al.Practical mathematical representation of the flow due to a distribution of sources on a steadily advancing ship hull［J］.Journal of Engineering Mathematics，2011，71:367-392.

［13］BAAR J J M，PRICE W G.Evaluation of the wavelike disturbance in the Kelvin wave source potential［J］.Journal of Ship Research，1988，32(1):44-53.

［14］MARR G P，JACKSON P S.Some improvements and comparisons in the solution of the Neumann-Kelvin problem［J］.Journal of Ship Research，1999，43(3):170-179.

［15］MARR G P.An investigation of Neumann-Kelvin ship wave theory and its application to yacht design［D］.Auckland:University of Auckland，1995.

［16］XU Yong ，DONG Wencai.A fast integration method and characteristics research for 3-D translating-pulsating Green’s function of Havelock form in deep water［J］.China Ocean Engineering，2011，25(3):365-380.

［17］姚朝帮，董文才.开尔文源格林函数数值积分方法研究［J］.上海交通大学学报，2014，48(1):98-105.YAO Chaobang，DONG Wencai.Evaluation method for Kelvin Source Green＇s function［J］.Journal of Shanghai Jiaotong University，2014，48(1):98-105.

［18］叶伟，陆鑫森.频域有航速Green函数及其梯度的数值计算方法［J］.上海交通大学学报，1996，30(10):1-8.YE Wei，LU Xinsen.Numerical calculation of the Green’s function and its gradients with forward speed in the frequency domain［J］.Journal of Shanghai Jiaotong University，1996，30(10):1-8.