水流中船舶单双锚泊偏荡运动响应研究

汤健勇，王飞

(上海交通大学海洋工程国家重点试验室，上海200030)

船舶锚泊操纵性能是操纵性研究中的一个基本方面，和安全性能密切相关。锚泊状态下船舶往往因风流等环境因素的影响，而左右偏荡，此时锚泊设备会承受很大的动态载荷，锚链张力数倍增加，时而引起走锚、断链等事故的发生。为了减小船舶偏荡运动，提高锚泊安全性，常采用以下方法［1］:改单锚泊为双锚泊(八字锚、一字锚、止荡立锚等)，微速动车，使用侧推等。然而船舶锚泊运动性能影响因素众多，缺乏较为有效的理论分析支持手段，不同锚泊形式的偏荡运动响应特性及规律也不是很明确。

船舶锚泊运动研究包括船舶自身操纵性和锚链动力学研究两部分。船舶自身操纵性的研究很早就已展开，众多学者对船舶在各种情况下的操纵运动进行了广泛的研究［2］;对单独锚链动力学的研究也有较多的涉及［3-5］，采用的方法有悬链线、弹性缆索或集中质量法等。而锚泊操纵性能由于综合了船舶水动力性能和锚链动力学，模型试验及实船试验均难以展开，在此方面的研究多以实船经验总结［1，6］和一些理论分析计算［7-8］为主，且这些研究基本是针对船的单锚泊运动，而不同形式锚泊运动的研究很少有人展开。

为此本文围绕船舶锚泊运动展开研究工作，通过数值仿真研究各种不同锚泊形式下，船舶在水流中的偏荡运动响应规律，总结各因素对于运动的定性规律，探讨提高船舶锚泊安全性的建议方法。本文主要围绕船舶锚泊操纵性能展开研究工作，系统地研究不同锚泊形式运动响应特性。给出时域内比较通用的船舶动态锚泊运动数学模型，采用数值仿真研究方法，针对船舶单锚、八字锚、一字锚等各种锚泊形式，研究其运动响应特性，总结运动规律，探讨提高锚泊安全性的方法，以期给出一些规律性结论以及有实际意义的结果。

1 三维动态运动数学建模

图1 船舶锚泊系统示意图Fig.1 Diagram of anchored ship with dual bow anchors

锚泊船系统示意图如图1所示，整个系统由水面船舶、锚链以及海底的锚几个部分组成。本文中水面船舶采用MMG运动模型，只考虑3个方向上的运动，锚链采用最为基本的集中质量法建模以准确描述偏荡过程中链和海底之间的相互作用力。为简化问题，船舶偏荡中不考虑走锚问题。图1中:s为锚链长度坐标，其零点位于下端的锚上，整个锚链的长度记为S，也即出链长度;ψ水面船舶的艏向角，为顺时针偏离y轴的角度;J为水流的速度向量，流向角记为Jψ;锚链微元在三维空间下的姿态角表示为(θ，φ)。惯性坐标系统(x，y，z)和船体运动坐标系(ξ，η，ζ)，用以建立系统的运动控制方程，其中惯性坐标系原点取在水面上;而船体运动坐标系，原点取在船舶重心位置处，纵轴ξ指向船艏，横轴η指向右舷，而垂轴ζ则指向下方。这2个坐标系统之间可通过船舶的艏向角ψ相互关联，写为矩阵形式为

1.1 锚泊状态下船舶运动数学模型

本文根据 MMG建模思想［2，9］，忽略对锚泊运动无宏观影响的纵摇、升沉及横摇运动，可得到船舶的三自由度运动控制方程，即

式中:m、Ⅰzz分别为船舶的质量及转动惯量;mx、my、Jzz为船舶在水中运动时的纵向、横向及艏向附加质量;(u，v，r)为船舶的纵向、横向及转艏速度，其上面的点表示对时间求导，即运动加速度;X为作用在船体纵向上的作用力，Y为横向作用力，N为转艏力矩;下标H、R、P、C分别表示船体、舵、桨及锚链的作用力。其中，锚链的作用力将在后面作为船-链动力耦合边界条件的形式给出;螺旋桨作用力因其无转速，可作零处理。其他作用力如下文。

1.1.1 船体水动力

将作用在船体上的水动力分为常速、低速及过渡状态分别计算，过渡状态水动力采用差值处理。

在常速域，根据井上模型，船体水动力为

式中:R(u)为船舶阻力，Xvr、Xvv、Xrr船体纵向水动力系数;Yv、Yr、Nv、Nr为线性水动力系数，Yvv、Yvr、Yrr、Nvv、Nv v r、Nv rr为非线性水动力系统;各水动力系数确定方法可参见文献［2，9］，这里不再赘述。

而在低速域转艏角速度或漂角较大时，水动力性能将会发生明显变化;考虑到船舶自身低速运动并非本文要点，根据文献［10］，采用基本的横流模型来确定作用在船体上的水动力，纵向、横向作用力和转艏力矩可近似表示为

式中:d为船舶的吃水;CD0为横流阻力系数，可近似为

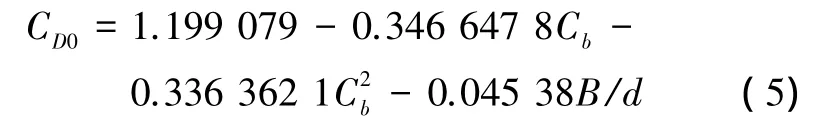
式中:Cb是方形系数，B/d是宽度吃水比。

而水流对船舶运动的影响，因其在作用结果上相当于改变了船体和水之间的相对运动速度，故本文确定其影响时，不直接处理，而将相对运动速度代替船舶对地速度溶入操纵运动控制方程(2)中;它们之间的相对运动速度(ur，vr，rr)为

1.1.2 舵力的计算

不考虑桨舵耦合作用，此时舵上的作用力可近似处理为

式中:FN为舵的法向力，可采用藤井公式计算，xR为舵纵向坐标;aH为操舵诱导船体横向力与舵力之比值，这些系数参见文献［2］。

1.2 锚及锚链动态运动控制方程

船舶在锚泊操纵运动过程中，锚及锚链在水下的运动是一种三维的动态运动，且同海底之间存在着各个方向上的作用力，为准确反映其运动，本文采用最基本的集中质量法对其进行建模，并计入水流、海底摩擦力等各种作用力的影响。

根据集中质量法基本原理，对抛锚的每一根锚链，将其从下端锚开始到上端锚链孔处离散为K段，共K+1个节点，其中下端s=0为锚，对应第i=0个节点，上端s=S为第i=K个节点。

对第i个节点应用牛顿第二定律，得锚链节点的基本运动控制方程［8］，即

式中:Mi为质量矩阵，包括锚链节点自身的惯性质量及其在水中的附加质量Mai，x¨i为它的加速度，它们可分别表示为

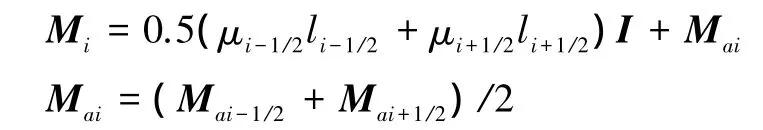
式中:Ⅰ为3×3的单位矩阵;m、l分别为锚链单位长度的质量、节点间长度;下标i+1/2表示节点i和节点i+1间的物理量，如li+1/2表示节点i和节点i+1间的长度，即li+1/2=si+1-si。F为作用于节点上的所有外力，包括基本的锚链张力T、浮力B、重力G、流体阻力D、海底摩擦R力及海底反作用力P，各作用力的确定参见文献［8］。

1.3 船-锚链耦合条件

在船舶锚泊操纵过程中，锚链与船舶之间存在着相互的影响;一方面各个锚链孔处锚链节点的位置速度始终同船舶的位置速度一致;而另一方面锚链上的张力又会影响到水面船舶的操纵运动。本文中不论单锚泊还是双锚泊，耦合条件均一致，它们之间的这2种影响如下文。

1.3.1 运动耦合条件

在每个锚链孔处，锚链节点在惯性系下的位置速度以矩阵形式表示为

式中:(xg，yg，zg)表示水面船舶在惯性坐标系下的位置，(xt，ht，zt)为船体坐标系下锚链孔的坐标。

1.3.2 动力耦合条件

在船体运动坐标系下锚链对船体的作用力为

式中:(Tsx，Tsy，Tsz)为惯性系下锚链上端的张力。

1.4 链(锚)-海底动力条件及抓力

当锚及锚链着底后，还会受到海底的额外作用力作用，即法向上的海底反作用力P和切向上的摩擦阻力R。

1.4.1 锚链力的确定

对于锚链节点(i＞0)，当其着底后，作用在锚链节点上的反作用力P［11］可表示为

而摩擦力R根据不同锚链节点的运动状态(运动、静止及过渡)，分别为

式中:kc为锚链同海底之间的摩擦阻力系数。

1.4.2 锚抓力的确定

同锚链相比，锚(i=0)着底后的作用力不仅有基本的海底反作用力和摩擦阻力，还包括啮土后的作用力增量，增量系数记作ki，则锚的反作用力可采用如下方法近似确定:

当Pi=0不为零时，摩擦力R根据不同的运动状态(运动、静止及过渡)，分别为

式中:ka为锚同海底之间的摩擦阻力系数，Rmax锚着底啮土后的最大抓力，Rmax=-PANnka(PAN+Pi=0)/|PAN+Pi=0|。

1.5 数值求解方法

船舶的运动控制方程(2)及锚链的控制方程(8)，再加上边界条件及速度的数学定义v=dx/dt，便组成了一个完整的偏微分方程组，

对于此控制方程，本文采用四阶龙格库塔方法在时域内积分求解。

2 数值计算与分析

选取一常规水面尾机型船舶作为仿真研究对象，采用数值方法对其进行锚泊操纵研究。针对不同的锚泊形式及止荡方法，分析船舶在流中的偏荡运动响应特性，并总结运动规律。

船舶主要参数为:船舶垂线长108 m，宽15.6 m，吃水 6.85 m，排水量 8 070 t，Cb=0.683，Cp=0.72，Cw=0.803，水深 25.0 m，水密度 1 025 kg/m3，在本文所考虑的速度范围内，阻力可近似为

船舶初始位置为(0，0，0)，艏向为零，船艏左右锚链孔在船体坐标系下坐标为 (54.0，±1.24，0)，舵面积AR=15.36 m2。

锚链参数分别为:链环直径 44 mm，破断力约1 000 kN，杨氏模量E=4.5×109Pa，单位长度质量体积分别为42.5 kg/m 和0.005 45 m2，流体阻力系数Cn=2.35，海底摩擦力系数kc=1.12，单位长度附加质量约为2.4 kg/m，其仅有法向上的质量，切向上的近似取为零。锚为无杆锚，惯性质量 2.6 t，体积0.333 m3，基本摩擦力系数 1.59，抓力增量系数 2.72。

2.1 单锚泊运动响应计算

本节首先给出船舶单锚泊时的运动响应，仅抛右锚，出链长度S=150 m，水流速度分别取为J=1、2、3 kn，方向沿y轴负方向，初始时船舶余速艏向均为零。图2为稳定后，船舶及锚链在不同时刻的空间运动视图，图3为在不同流速时，船中运动轨迹以及锚链上端张力。

图2 单锚泊船舶及锚链运动视图(J=2.0 kn)Fig.2 The spatial configurations of the ship and chain at single anchor moor(J=2.0 kn)

结果显示，当流速较小时船舶基本无偏荡运动，流速较大时偏荡幅度迅速增大，船舶中心运动轨迹为一个不对称的8字形或椭圆形(半8字形)，且靠近抛锚一侧的8字偏小有时甚至消失;偏荡运动引起的锚链张力同稳态值相比(即张力水平分量同阻力值R(u)相比)有数倍之差，峰值可达八倍之多，所以说偏荡运动是造成船舶断链走锚的主要原因之一;图3(b)显示，偏荡运动周期在2、3 kn时约分别为1 100、900 s，周期同流速呈反比关系。

为分析微速倒车对于船舶偏荡运动的影响，将螺旋桨倒车拉力设定为T=10kN，并认为其在偏荡过程中不变。图4给出了不同流速时的运动响应情况，其中1 kn流时船舶处于稳定状态，图5为有无倒车拉力时的运动结果对比。

通过对比可看出，加上倒车拉力后，其运动轨迹变为一个较规则的蝶形，船舶的偏荡宽度有一定程度的减小，但是链上的冲击张力幅度却有较大的增加，所以对于单锚泊船，通过微速倒车止荡，因链上张力增加较大，故其并不一定可以提高锚泊安全性能。

图3 单锚泊船舶运动响应Fig.3 Swaying response of the ship at single anchor moor

图4 微速倒车时单锚泊船舶运动响应Fig.4 Swaying response of the singly anchored ship at dead slow astern condition

图5 偏荡宽度及锚链张力峰值对比Fig.5 Comparison of the swaying breadth and tension peak at dead slow astern condition

2.2 八字锚(一点锚)运动响应

船舶抛双首锚，简便起见抛锚过程略去不作考虑，出链长度均为150 m。为考虑不同张角对锚泊船运动的影响，两个锚在海底的坐标(x，y，z)分别取5组:

组一(± 0.0，54.0，-25.0)，此时为一点锚

组二(±30.0，54.0，-25.0)

组三(±50.0，54.0，-25.0)

组四(±70.0，54.0，-25.0)

组五(±90.0，54.0，-25.0)

而水流速度依次取为 1.0、2.0、3.0、4.0 kn，方向同船舶初始艏向相对。不同张角对偏荡宽度和锚链上端张力峰值的影响由图6给出，其横坐标为2个锚的x向坐标值，用以间接表示八字锚的张角。

结果显示，采用八字锚后，船舶的运动轨迹是一个比较理想的八字形，相同水流速度时的偏荡宽度较单锚泊系统减小近一半，止荡效果比较明显;同时可以看出八字锚张角的影响为，偏荡宽度整体上随张角开始微幅增大而后才减小，且当张角超过一定程度后才有明显减小;而锚链张力峰值随张角增大而近似线性增大，但当张角较大时，因八字锚的止荡作用，链上张力增加程度有限。

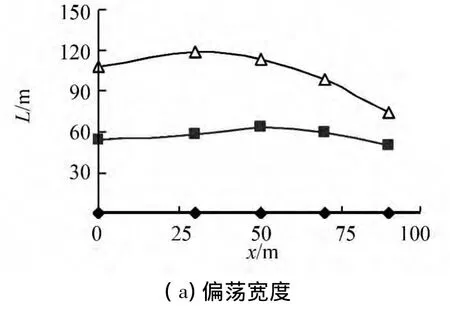
图6 不同张角时八字锚偏荡宽度及张力峰值Fig.6 Swaying breadth and chain＇s peak tension at different anchor＇s positions

图7 微速倒车时八字锚偏荡运动响应(锚坐标x=±30)Fig.7 Swaying response of the anchored ship at dead slow astern condition(anchor x=±30)

计算中发现，八字锚偏荡运动模式并不唯一，在同一状态会表现出2种不同的模式，即对称的八字形模式和椭圆形模式(尖头方向左右均有可能)，究其原因可能是不同的初始条件所致。

倒车拉力设为10 kN，流速和各组锚坐标位置同上面一样。图7给出了锚坐标为x=±30.0时的运动响应情况，图8为不同张角时船舶的偏荡宽度和锚链上端张力峰值。

结果显示对于八字锚，当采用微速倒车提供一个倒车拉力后，船舶偏荡的宽度有大幅减小，且随着八字锚张角的增大，减小幅度也越大，船舶甚至不再左右偏荡;而此时链上的张力也因为倒车拉力的止荡作用而减小，特别是张角较大的时候。故大张角八字锚结合微速倒车是提高锚泊安全性的一种理想的方法。

图8 微速倒车时八字锚偏荡宽度及张力峰值Fig.8 Swaying breadth and tension peak at different anchor＇s positions and dead slow astern condition

2.3 一字锚运动响应

一字锚是适于内河中的一种锚泊方法，其偏荡幅度小，经验中其优点是能够最大程度的限制锚泊船船首的运动范围。本节中，右锚作为力锚，出链150 m，左锚作为惰锚，出链100 m，2个锚的坐标分别为(0，188，-25)和(0，-26，-25)。流速取为J=1.0，2.0，3.0 kn，船舶顶流抛锚，忽略中间过程，直接认为两锚已抛于预定位置，计算结果如图9所示。

图9 一字锚偏荡运动响应Fig.9 Swaying response of the ship at the Bahamian moor

结果显示，同单锚泊运动响应相比，流速较低时(小于等于2 kn)，一字锚船的偏荡幅度可大幅减小，而锚链上的张力无明显增加;但当流速较大时，虽然偏荡幅度有一定程度减小，但是链上的冲击张力却有很大程度的增加，此时很有可能导致船舶走锚事故的发生，故在强流中一字锚的安全性能难以保证而不推荐采用。

2.4 止荡锚运动响应

抛双首锚，其中右锚为长链，出链150 m;左锚出链1节(27.5 m)，作为止荡立锚使用。下面分别给出了不同流速J=2.0、3.0、4.0 kn 时，系统的运动轨迹和右链张力。计算结果如图10所示，其中2 kn流时止荡锚作用几何关系尚没有完全体现，其偏荡轨迹显得不规则。

结果显示，此时船舶仍然会偏荡，运动轨迹为一个八字形;但同前面单锚泊运动相比可以看出，由于止荡锚的作用，船舶偏荡运动幅度减小50%以上，同时锚链上的张力也相应大幅降低。计算中还显示，偏荡过程中短链锚多次和长链相接触，有可能导致锚链缠绕。

3 结论

本文采用数值仿真研究方法，系统地分析了水流中单锚、八字锚、一点锚、止荡锚等不同形式锚泊船的运动响应特性。研究结果显示:

1)船舶偏荡运动引起的冲击张力数倍于静态值，是造成船舶断链走锚的主要因素之一;

2)八字锚在流中的偏荡宽度约为单锚泊的一般左右，随着张角的增大，船舶的偏荡开始微量增加而后逐渐减小;

3)微速倒车对于单锚泊和八字锚均有止荡效果，特别是八字锚时可大幅减小偏荡宽度，且此时链上张力随八字张角的增大而整体上减小;

4)而一字锚在流速较低时有良好的止荡效果，但流速高时链上张力增加幅度很大而不推荐使用;

5)止荡锚在减小船舶偏荡运动和锚链张力方面均有效果，但可能造成锚链缠绕。

同时结果显示，在某些条件下船舶偏荡运动模式不唯一，可能为8字形，也可能为椭圆形(半8字形)。

［1］洪碧光.船舶操纵［M］.大连:大连海事大学出版社，2007:267-285.

［2］范尚雍.船舶操纵性［M］.北京:国防工业出版社，1988:5-23.

［3］SCHELLIN T E.Mooring load of a ship single-point moored in a steady current［J］.Marine Structure，2003，16:135-148.

［4］COZIJN J L，BUNNIK T H J.Coupled mooring analysis for a deep water calm buoy［C］//OMAE 2004，23rd International Conference on Offshore Mechanics and Arctic Engineering.Vancouver，Canada，2004:1-11.

［5］THOMAS D O，HEARN G E，NEWCASTLE U.Deep water mooring line dynamics with emphasis on seabed interference effects［C］//OTC-7488 26th Offshore Technology Conference.Houston，USA，1994:203-214.

［6］云会杰，杨天华.论锚泊船舶的偏荡与防止［J］.天津航海，2011(3):12-13.

［7］张玉喜，洪碧光，杨林家，等.锚泊船在风流中的偏荡运动研究［J］.大连海事大学学报，2009，35(4):25-29.

［8］王飞.船舶锚泊操纵运动预报与分析［J］.上海交通大学学报，2012，46(8):1210-1217.WANG Fei.Dynamic prediction and analysis on mooring maneuver of ship［J］.Journal of Shanghai Jiaotong University，2012，46(8):1210-1217.

［9］HIRNAO M.On calculation method of ship maneuvering motion at initial design phase［J］.Journal of the Society of Naval Architects of Japan，1980(147):144-153.

［10］乐美龙.船舶操纵性预报与港航操纵运动仿真［M］.上海:上海交通大学出版社，2004:6-15.

［11］WANG F，ZHANG G L，DENG D H，et al.A study on dynamic response of cable-seabed interaction ［J］.Journal of Shanghai Jiaotong University:Science Edition，2009，14(4):443-449.