基于最小描述长度的图分割变化检测改进算法

魏长宝，姚汝贤

（黄淮学院信息工程学院，河南驻马店463000）

·图形图像处理·

基于最小描述长度的图分割变化检测改进算法

魏长宝，姚汝贤

（黄淮学院信息工程学院，河南驻马店463000）

图分割变化检测（GPCD）可检测出可能导致网络社区发生变化的重要事件。针对现有的检测算法未考虑图形分割结构动态特点的不足，利用概率树表示图分割结构的概率模型，将GPCD问题转化为基于最小描述长度的树变化检测问题，并提出一种求解GPCD问题的Tree算法。仿真实验结果表明，与GraphScope基准算法相比，该算法检测图分割结构变化时的虚警率较低，并具有较高的检测精度。

图分割变化检测；最小描述长度；概率树；变化成本；虚警率

中文引用格式：魏长宝，姚汝贤.基于最小描述长度的图分割变化检测改进算法［J］.计算机工程，2015，41（7）：274⁃279，284.

英文引用格式：Wei Changbao，Yao Ruxian.Improved Algorithm of Graph Partitioning Change Detection Based on M inimum Description Length［J］.Computer Engineering，2015，41（7）：274⁃279，284.

1 概述

图分割技术［1⁃3］（也称图聚合问题）是一种按照某种标准将图分成若干子模块的方法。图分割可以使得分割后各子模块中节点联系更紧密，模块间联系更低。该技术在蛋白质网络、网络数据挖掘等许多领域都有广泛应用。本文主要研究如何对二分图时间序列的图分割结构变化进行检测。将该检测问题称为图分割变化检测（Graph Partitioning Change Detection，GPCD）问题。根据链路关系，图分割结构可看成图节点的聚类结构。这一图分割过程将会导致多个网络社区。因此，它有助于社区结构变化检测及图分割结构变化检测，而社区结构变化往往对应于真实世界中的重要世界，因此研究GPCD问题具有重要意义［4⁃5］。

文献［6⁃7］基于最小描述长度（MDL）原则，从无损数据压缩角度为选择最优分割提供了一种准则。该准则认为，如果有种分割策略，进行图形编码时所需总码长及相对数据量最小，则该分割策略即为最优分割。为此，文献［8⁃9］提出基于MDL的静态二分图分割方法和普通图分割方法。对于动态图分割，文献［10］提出 GraphScope图形变化检测算法。该方法根据MDL准则将二分图分割为一组子图，以便使数据的码长及图形分割码长之和最小，通过进行分割是否发生变化的假设性检验来实现图形分割结构的变化检测。GraphScope是GPCD问题的有效求解算法，但是存在如下缺陷：（1）初始图必须是节点分割的直积，图形分割结构的表示非常有限，本文将这一现象称为基于直积的分割策略。当描述具有分层特征的图分割结构时会出现大量参数，比如进行一次分割后，对每个被分割的子图还需再一次分割，依次类推。（2）没有考虑图形分割结构的动态特点。实际上，该方法也没有考虑分割转换概率模型。因此，图形变化的成本被忽略，导致出现虚警。

为此，本文提出针对GPCD问题的一种新的求解算法TREE，主要工作如下：（1）基于树进行图分割：TREE算法利用基于树的概率模型来表示图形分割结构，本文称其为基于树的分割方法，GPCD问题可转化为树结构的变化检测问题。与基于直积的分割方法相比，基于树的分割问题可使本文使用较少参数来表示分层分割图。（2）GPCD问题的动态模型选择：通过引入图分割之间的转换概率，以考虑基于树的图分割的动态特性。于是，图分割变化成本可定义为转换概率的码长。然后，本文将动态模型选择（DMS）理论［11］应用于图分割序列选择过程中，即通过选择一组图分割，可使数据的码长与变化成本之和最小。因此，根据数据拟合和变化复杂度间的平衡情况确定最优序列。

2 图形分割变化检测

假设图形序列为：

其中，每个二分图Gt（t＝1，2，…）有m个发送节点和n个接收节点。更准确地说，每个Gt可表示为一个m×n矩阵，第（i，j）个元素gij表示第i个发送方至第j个接收方的链接。本文假设m和n固定。下面分析如何将图形序列Ψ分割为如下一组图形子序列：

其中，每个Ψs表示从ts至ts+1-1的一个图形序列：

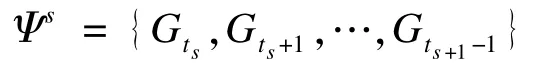
ts称为变化点，Ψs称为一个分段（s＝1，2，…）。将图 G的分割看成图 G分解为一组连接子图｛G（u）｝的过程，其中G＝∪uG（u）。可得GPCD问题定义如下：已知一个图形序列Ψ＝G1，G2，…，根据G1，G2，…的分割序列来检测出Ψ中的变化点及其相应变化。

3 基于树的GPCD问题

3.1 基于树分割的概率模型

本文利用二分树来实现基于树的分割表示。在二分树中，每个树节点关联一组发送节点和接收节点。为了区分树中节点和图中节点，将前者称为树节点，将后者称为节点。对每个树节点，其子树节点的分配有2种情况。情况1：2个子树节点的发送节点集合相同，但是接收节点集合分离。情况2：2个子树节点的接收节点集合相同，但是发送节点集合分离。

例如，如果图 G的矩阵表示如式（1）所示，则图G可由图1中的二分树确定。首先接收方节点集合可分为｛1，2｝和｛3，4｝，然后对于具有前一集合的子树节点，接收节点集合可分为｛1，2｝和｛3，4｝。

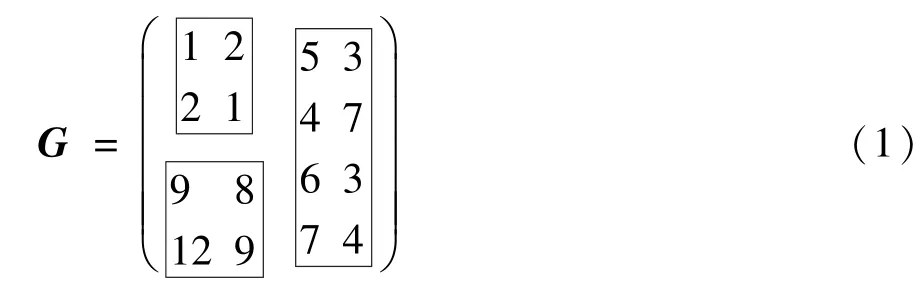
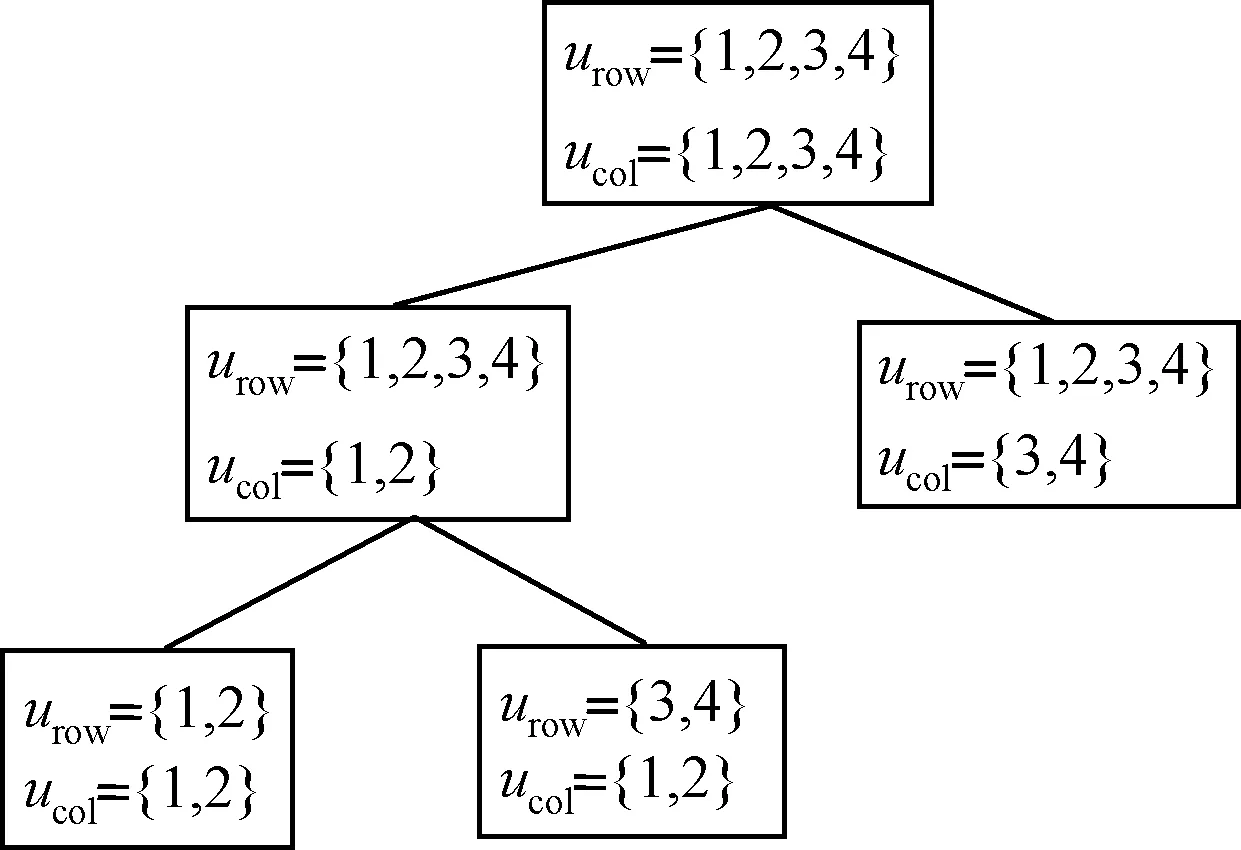
图1 基于树的分割过程

已知树M，设u＝（urow，ucol）表示树M中叶子u的行节点和列节点组成的元组。设G（u）表示u的相应子图。此时，可以获得一种基于数的分割G＝∪uG（u）。

设Mt表示 Gt的对应树，二分树序列可表示如下：

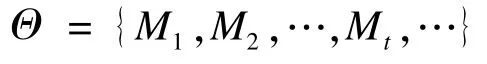
Ψ的分割问题转化为Θ的分割问题（如图2所示），本文将Θ的分割表示为 Θ ＝｛Θ1，Θ2，…｝。 对每个s，任意M，M′∈Θs有M＝M′。如果Gt∈Ψs，则Mt∈Θs。也就是说，一个分段只对应于一个树。

图2 基于树的图分割变化检测

设M表示图G相应的二分树。M的概率分布定义可表示如下：对树M中的叶子u，Gr，c（u）表示u相应子图中第r行第c列的元素。假设根据参数为λ（u）的泊松分布生成 Gr，c（u），并将其表示为

3.2 动态模型选择

假设已知图形序列Ψ＝G1，G2，…，GT（T：数据规模）及基于树的分割序列Θ＝M1，M2，…，MT，其中Mi会随着时间而变化。假设每个码字不是另一码字的前辍，在此前提下考虑ψ和Θ的编码问题。本文引入动态模型选择（DMS）准则［8］来衡量已知 ψ时Θ的质量。将其定义为对ψ和Θ进行编码所需要的总码长L（Ψ；Θ）。

其中，M0已知；式（3）右侧第1项表示Ψ相对于Θ的码长；第2项表示Θ本身码长。DMS可看成是将传统的基于MDL的静态模型选择拓展为一种模型序列选择［11］。

3.3 基于树的图形分割编码方法

下面分析计算式（3）右侧第1和第2项。Mt已知时Gt的码长可计算为归一化最大似然（NML）码长，该码长定义为归一化最大似然的负对数，如下式所示：

其中，leaf（Mt）表示Mt的一组叶节点；Gt（u）表示第u个叶节点的子图。设 Gt：r，c（u）表示 Gt（u）的第（r，c）个元素。设urow和ucol分别表示树节点u的行节点集合和列节点集合。于是，PNML表示归一化最大似然分布，定义如下：

式（5）右侧的分母难以进行解析计算，根据Rissanen方程［12］进行近似计算：设I（λ）表示定义为的Fisher信息矩阵，Gt的随机复杂性有如下等式：

其中，a表示最小整数，λ＾∈［0，2a］且lb×a＝lb a+ lblb a+…+lb b表示对a编码时需要的码长，此时对所有正项求和，且lb b≈2.865 064。如果数据范围无限，则Fisher信息发散，因此本文将其限制在范围［0，2a］内以便使整数有限。 将式（6）代入式（4），可得：

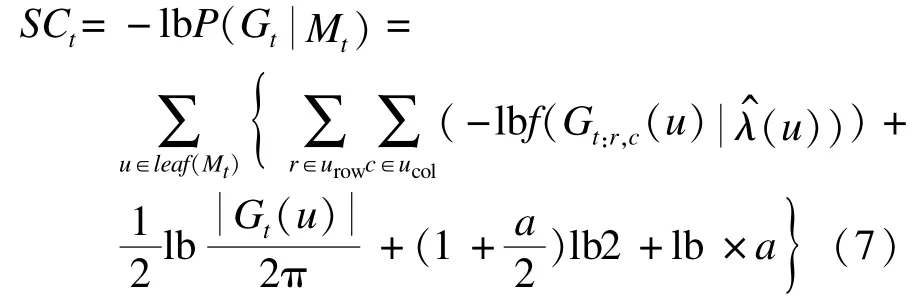
3.4 树转换的编码方法

下面给出式（3）中第 2项的计算方法。设α（＞0）表示一维参数。设No（Mt）表示Mt中叶节点的数量，N1（Mt）表示 Mt中内部树节点的数量，且：

用int（Mt）表示Mt的内部树节点集合，mu表示在树节点u处可被分割的树节点数量。转换概率定义如下（对t≥1）：

该转换定义表明，树节点不发生变化的概率为1-α，发生变化的概率为α。在后一种情况下，根据概率选择 Mt。因此，树转换的码长为：

此时，每次转换时树编码方法与 Rissanen方法［12］吻合，于是有：

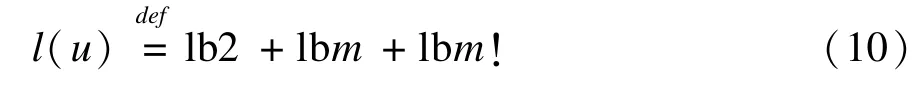
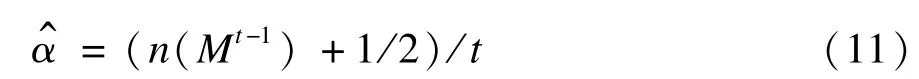
其中，n（Mt-1）表示Mt-1中树的变化总量。

3.5 基于树的GPCD问题

下面介绍本文提出的TREE算法，该算法的总体流程如下：

（1）通过分割和融合操作来构建一个树序列：本文利用图序列来构建树序列。树序列包括多个子序列，每个子序列称为一个段。假设在同一分段内的所有树相同，且对不同的时间分段，一个段中的树与相邻段中的树不同。为了构建每个段中的树，对节点进行分配，对树进行分割或修剪操作以使随机复杂性最小。具体内容见算法1～算法3。

算法1 节点分配

已知：图形子序列Ψs，对叶节点u，有一组行节点：u1row，u2row

步骤1 设置R＝u1row∪u2row。

步骤2 设置x（∈R）为一个列节点，设置R←R-｛x｝

步骤3 计算：

步骤4 计算 KL（λx，λ1），KL（λx，λ2），其中，表示参数λ1和λ2时泊松分布间的Kullback⁃Leibler散度。

步骤5 如果 KL（λx，λ1）＜KL（λx，λ2）且 x∈u2row，则u1row←u1row∪｛x｝，u2row←u2row-｛x｝，否则如果KL（λx，λ2）＜KL（λx，λ1）且 x∈u1row，则 u2row←u2row∪｛x｝，u1row←u1row-｛x｝，否则保持不变。

步骤6 如果R＝Ø，则终止，否则执行步骤2。

（2）对树序列进行最优分段：为了使总码长最小，根据式（3）DMS准则对树序列进行分段。按照如下方法确定一个变化点序列。对已知分段Ψ，Ψ的随机复杂度（SC）定义为：

其中，Mt表示Gt的树。设SCs表示最后一个分段Ψs的随机复杂性，SCs+t表示Ψs∪Gt的随机复杂性，SCt表示Gt的随机复杂性，表示从一个段到另一个段的转换概率估计。将式（3）DMS准则应用到树序列的分割中。于是发现，如果：

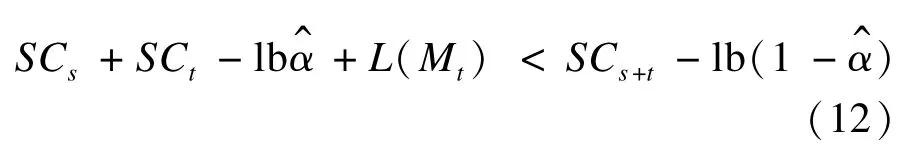
则可将时间t看成是一个变化点，否则不将其看成变化点。此时：

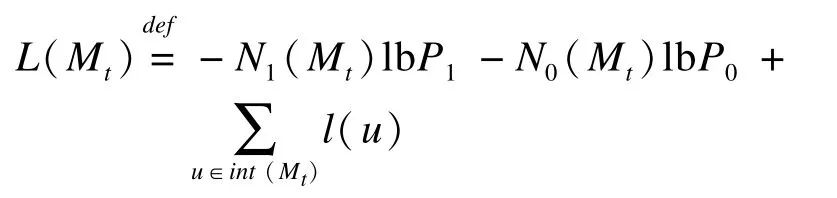
鉴于两者间的时间差异，通过式（3）DMS准则和式（9）可推出式（12）。此外，Gt的变化点指数可定义为：

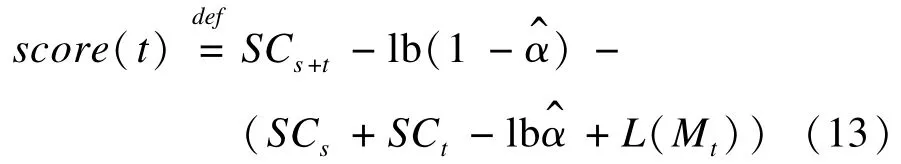
该指数可衡量在时间t进行分割时码长的下降情况。本文定义，只要下式成立则t即是一个变化点。

TREE的时间复杂度为O（mn（lb mn）T），其中，m表示列的数量；n表示行的数量；T表示数据规模。这是因为每个树进行分割和融合的计算复杂度为O（mn），树的最大规模为O（lb mn），TREE算法运行时与T呈线性关系。

算法2 树分割

已知：u：双支树的一个叶节点

步骤1 对叶节点u，生成新的叶节点u1，u2，并设置u1row＝urow，u2row＝Ø。

步骤2 SC1＝SC（u1）+SC（u2）。

步骤3 对x∈u1row，计算将x从u1移动到u2时所生成的树的SC，并将其记为SC2。

步骤4 如果 SC2＜SC1，则 u1row←u1row-｛x｝，且u2row←u2row∪｛x｝。

步骤5 对所有 x（∈u1row），重复步骤 2～步骤4。

步骤6 对u1，u2，运行算法1。

步骤7 如果SC（u1）+SC（u2）-lb P0+ℓ（u）＜SC（u）-lb P1，则分割列节点。

算法3 树融合

已知：u：树的根，q：队列

步骤1 q＝｛u｝。

步骤2 u′←q.dequeue，d：u′的深度。

步骤3 设u1，u2是u′的子树节点。

计算：

SC1＝SC（u′）-lbP1

SC2＝SC（u1）+SC（u2）-lbP0+l（u）

步骤4 如果SC1＜SC2，则修剪u1，u2，否则q.enqueue（u1，u2）。

步骤5 重复步骤2～步骤4直到q＝Ø。

4 基于直积的GPCD算法

GraphScope算法是一种典型的基于硬聚类的GPCD算法。它首先分别对接收节点和发送节点进行聚类，然后生成一个图形分割作为发送节点和接收节点聚类的直积。文中将这种分割称为基于直积的分割。例如，假设发送节点集合为｛A，B，C，D｝，接收节点的集合为｛1，2，3，4｝。当为接收节点生成｛A，B｝和｛C，D｝2个聚类，并为接收节点生成｛1，2｝和｛3，4｝2个聚类时，生成的分割策略有4个区域分割成为它们的直积，如图3所示。

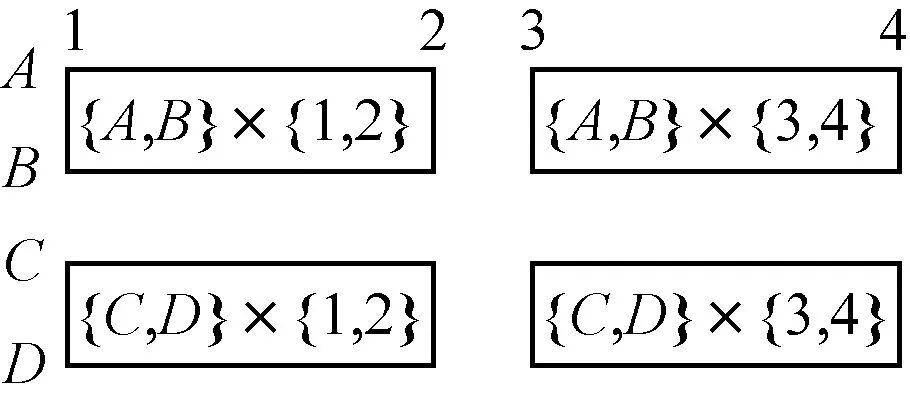
图3 基于直积的分割

GraphScope算法使用多种启发式策略来构建基于直积的分割，此时总码长在所有可能的分割中局部最小。

GraphScope的计算复杂度为O（mnT（k∗+1∗）），其中，k∗表示列聚类数量；1∗表示行聚类数量。

5 仿真实验

5.1 基于人工数据集的实验

利用人工数据集来比较TREE和GraphScope算法。设置接收节点和发送节点数量均为20个，并准备4个数据集，每个数据集有30个数据。根据Θ1生成t＝1～10之间的数据，根据Θ2生成t＝11～20间的数据，根据Θ3生成t＝21～30间的数据。变化点为tc＝11和21。

生成数据集1，2，3，4，其分割结构变化如图4～图7所示。

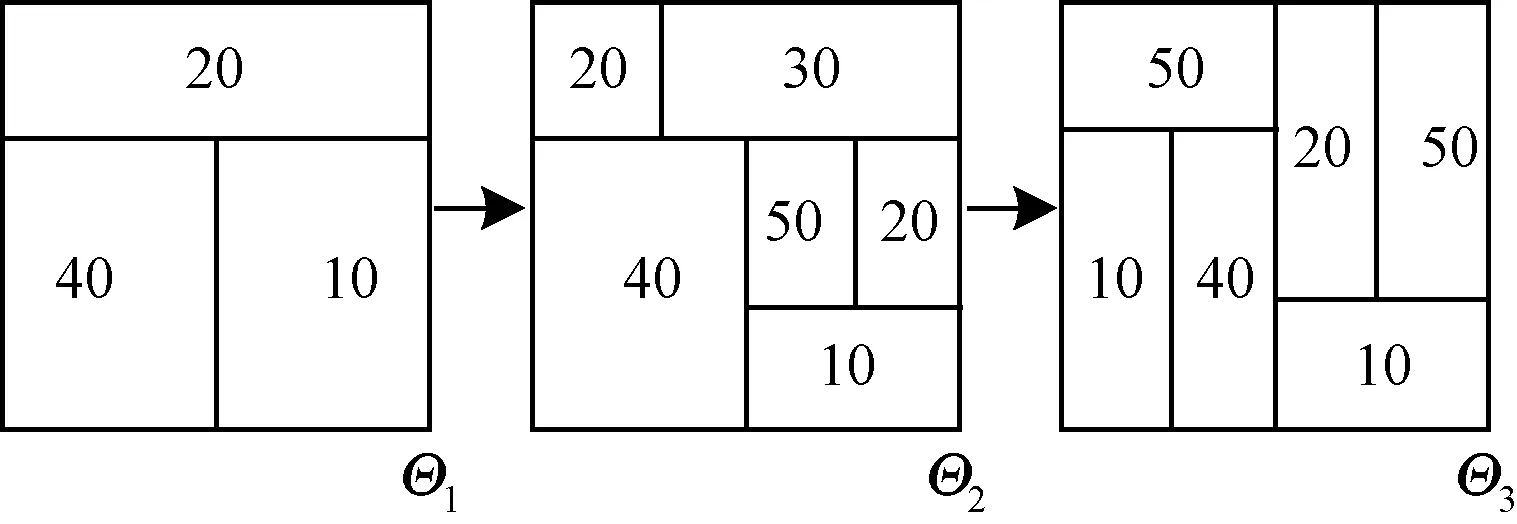
图4 数据集1分割结构变化

图5 数据集2分割结构变化

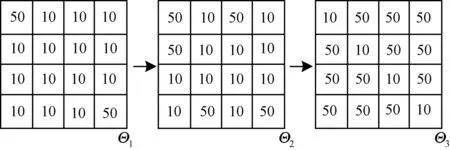
图6 数据集3分割结构变化

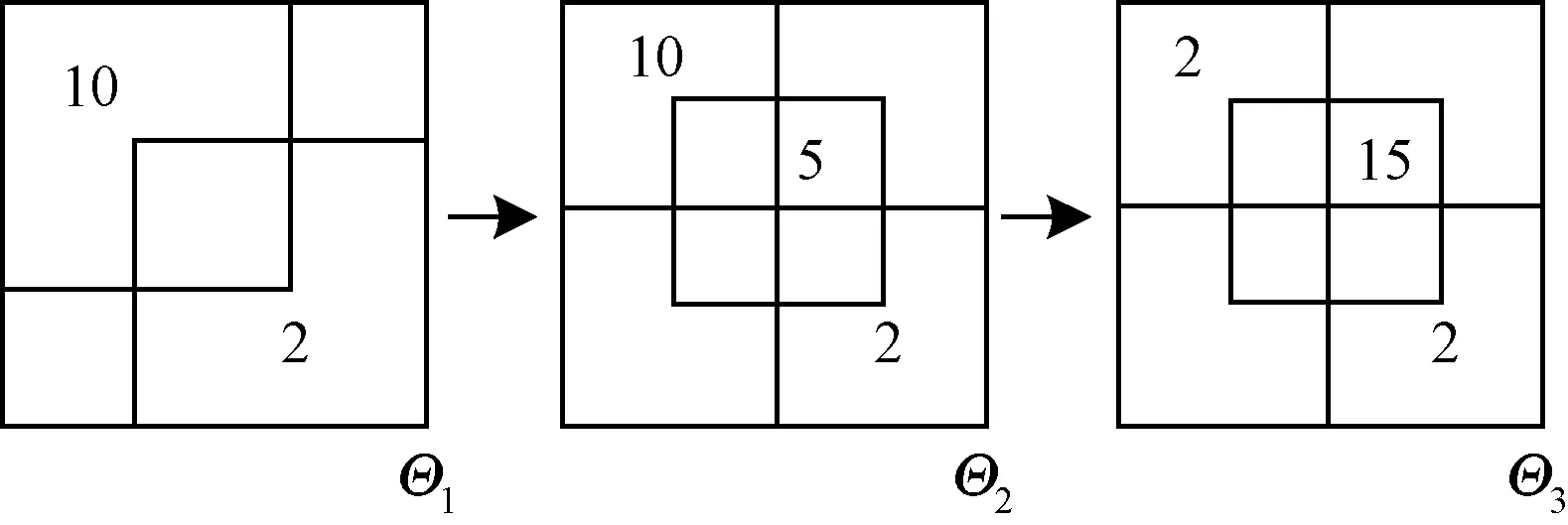
图7 数据集4分割结构变化

矩阵中的数据表明各分段的数量。使用效益和虚警率（FAR）2个指标来衡量GPCD的性能。假设x表示被检测出来的变化点，tc表示真实点，x的效益定义为：

其中，T表示已知正数。当且仅当x与tc吻合时值为1，当增加时线性降为0。如果警报点大于T且离真实点很远，则认为警报丢失。FAR表示所有警报中不是变化点的警报比例。进行50次实验取均值。

表1给出了不同算法在4个数据集上的效益和虚警率比较结果。本文在计算效益时设置T＝3。

表1 数据集1～数据集4的效益和FAR

对数据集1，2种算法的效益值均较高，TREE的FAR值远低于GraphScope。这是因为直积方法无法有效表示真实的分割，导致GraphScope的FAR高于TREE。对数据集2，由于与数据集1同样的原因，GraphScope算法的FAR较高。然而，即使对数据集2，基于树的方法无法有效表示真实分割，TREE的FAR仍然远低于 GraphScope。对数据集 3，GraphScope的FAR低于TREE。这是因为直积方法非常有效地表示了真实分割，TREE方法需要更多的参数才能表示真实分割。在实践中这种情况比较罕见。从以上结果可以看出，除了直积可以有效表示真实分割的少部分情况外，TREE的性能优于GraphScope。

表2给出了不同算法在数据集1～数据集4上的内存占用量比较结果。实验环境为：CPU为酷睿3.4 GHz，内存容量为4 GB，W indows 7操作系统（64位）。从表2可以看到，TREE算法在4种数据集上的表现都要优于GraphScope算法。仔细分析其原因可知，这主要是因为GraphScope算法在描述具有分层特征的图分割结构时会出现大量参数，需要多次分割以保证检测的准确性，所以占用了较多的系统资源。而本文方法利用基于树的概率模型来表示图分割结构，并将动态模型选择（DMS）理论应用于图形分割序列选择过程中，与GraphScope算法相比，可以用较少参数来表示分层分割图，因此取得了更好的系统性能。

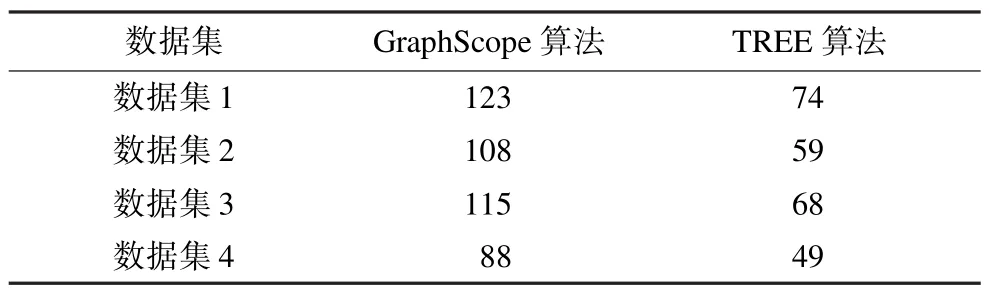
表2 不同算法的内存占用量比较 MB

5.2 基于真实数据集的实验

利用日本内务交通省、统计局、政策规划和统计研究及培训学院总干事提供的人口流动数据［14］进行实验。这一数据对公众开放，给出了2005年4月-2011年11月间日本所有县市每月人口流动情况。发送节点是人口流出的县市，接收节点是人口流入的县市。从发送节点到接收节点之间链路的数值表示一个月内从发送节点到接收节点间的流动人口数量。时间点总数为81，发送节点和接收节点总数均为47个。

图8和图9给出了2种算法的运行结果。每个图中的横坐标显示了 2005年4月开始的时间。图8、图9中的纵坐标表示变化点评分。在2种情况下，当纵坐标数值超过0时即可检测出变化点。2种算法均可检测出t＝71时的变化（从红色broken线可以看出）。该变化对应于2011年日本远东大地震导致的人口迁移。2011年5月检测出来的变化对应于日本政府宣布日本部分地区辐射水平显著升高时。2种算法还检测出了2011年6月和8月的变化，这2次变化对应于日本政府宣布2011年6月-8月间的人口流动。虽然TREE和GraphScope可以成功检测出重要真实事件的变化，但是GraphScope发布的与任何事件均无关联的虚警数量高于TREE。这表明TREE的稳定性优于GraphScope。

图8 TREE算法运行结果

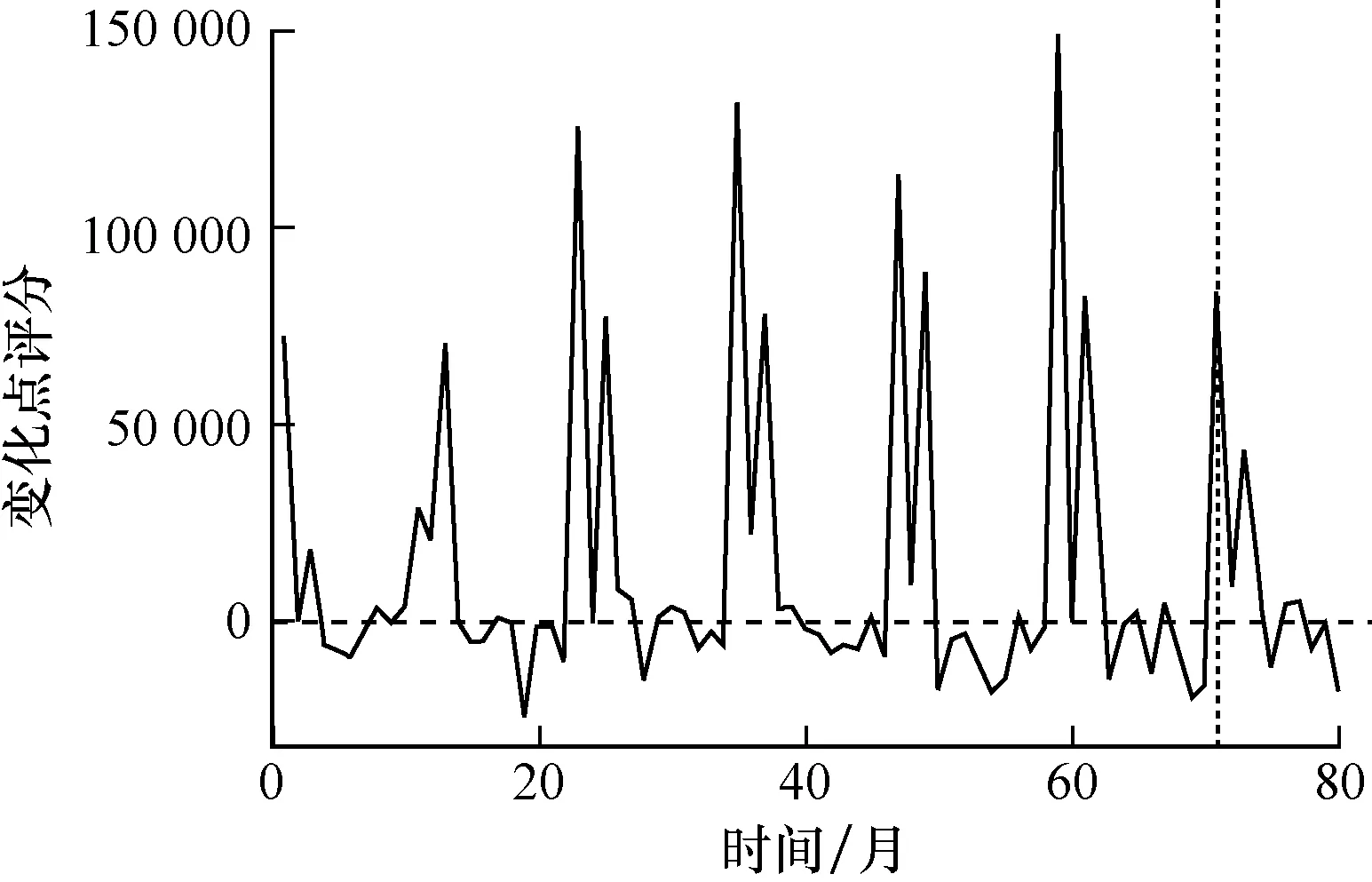
图9 GraphScope算法运行结果

6 结束语

本文主要研究了图分割变化检测问题，提出一种基于树聚类的GPCD求解算法TREE。该算法将传统的基于直积的方法（GraphScope）拓展至分割结构，具有分层特点。根据MDL准则，从动态模型选择角度设计本文算法，并与GraphScope算法进行比较，结果表明，对多种图形分割结构，TREE算法的GPCD性能优于GraphScope算法。下一步研究工作的重点是针对有权图分割时不能很好解决子图内部耦合度不高的问题，使用可以同时优化子图内部顶点耦合度和子图之间顶点耦合度的Ncut准则，提出基于散列技术的图分割改进算法。

［1］ 文政颖，于海鹏.基于多Gamma分布模型的 SAR图像直方图分割算法［J］.计算机工程与设计，2014，35（6）：2104⁃2108.

［2］ 汪云飞，毕笃彦，孙 毅，等.一种采用双势阱策略的小直径图分割方法［J］.计算机应用与软件，2013，30（4）：275⁃278.

［3］ Stanton I，Kliot G.Stream ing Graph Partitioning for Large Distributed Graphs［C］／／Proceedings of the 18th ACM SIGKDD International Conference on Know ledge Discovery and Data M ining.New York，USA：ACM Press，2012：1222⁃1230.

［4］ Bansal N，Feige U，K rauthgamer R，et al.M in⁃max Graph Partitioning and Small Set Expansion［J］.SIAM Journal on Computing，2014，43（2）：872⁃904.

［5］ Nishimura J，Ugander J.Restreaming Graph Partitioning：Simple Versatile Algorithms for Advanced Balanc⁃ing［C］／／Proceeding s of the 19th ACM SIGKDD International Conference on Know ledge Discovery and Data Mining.Chicago，USA：ACM Press，2013：1106⁃1114.

［6］ López⁃Ruiz R，Sanudo J，Romera E，et al.Statistical Complexity and Fisher⁃shannon Information：Applica⁃tions［M］.Berlin，Germany：Springer，2011.

［7］ Silva T C，Zhao L.Stochastic Competitive Learning in Complex Networks［J］.IEEE Transactions on Neural Networks and Learning Systems，2012，23（3）：385⁃398.

［8］ Chakrabarti D，Papadim itriou S，Modha D S，et al.Fully Automatic Cross⁃associations［C］／／Proceedings of the 10th ACM SIGKDD International Conference on Know ledge Discovery and Data M ining.New York，USA：ACM Press，2012：79⁃88.

［9］ Chakrabarti D.Autopart：Parameter⁃free Graph Partitioning and Outlier Detection［C］／／Proceedings of PKDD’04. Berlin，Germany：Springer，2004：112⁃124.

［10］ Sun J，Faloutsos C，Papadim itriou S，et al.Graphscope：Parameter⁃free M ining of Large Time⁃evolving Graphs［C］／／Proceedings of the 13th ACM SIGKDD International Conference on Know ledge Discovery and Data M ining.San Jose，USA：ACM Press，2007：687⁃696.

［11］ Yamanishi K，Maruyama Y.Dynam ic Model Selection w ith Its Applications to Novelty Detection［J］.IEEE Transactions on Information Theory，2013，53（6）：2180⁃2189.

［12］ Rissanen J.Fisher Information and Stochastic Comple⁃xity［J］.IEEE Transactions on Information Theory，2012，42（1）：40⁃47.

［13］ Haldar JP，Hernando D，Liang Z P.Compressed⁃sensing MRIw ith Random Encoding［J］.IEEE Transactions on Medical Imaging，2011，30（4）：893⁃903.

［14］ Jonsen ID，Flemming JM，Myers R A.Robust State⁃space Modeling of Animal Movement Data［J］.Ecology，2005，86（11）：2874⁃2880.

编辑 索书志

Im proved Algorithm of Graph Partitioning Change Detection Based on M inimum Description Length

WEIChangbao，YAO Ruxian
（School of Information Engineering，Huanghuai University，Zhumadian 463000，China）

Graph Partitioning Change Detection（GPCD）problem is important in that it leads to discovery of important eventswhich cause changes of network communities.Aim ing at the disadvantages that the existing detecting algorithms do not consider dynamic graph partitioning structures，itemploys probabilistic trees to represent probabilisticmodels of graph partitioning structures，and reduces GPCD into the issue of detecting changes of trees on the basis of the M inimum Description Length（MDL） principle，and proposes Tree algorithm for solving the GPCD problem.Simulation experimental results show that the algorithm realizes significantly less False Alarm Rate（FAR）for change detection than the baselinemethod called GraphScope.And it is able to detect changesmore accurately than GraphScope.

Graph Partitioning Change Detection（GPCD）；M inimum Description Length（MDL）；probabilistic tree；cost of change；False Alarm Rate（FAR）

1000⁃3428（2015）07⁃0274⁃06

A

TP393

10.3969／j.issn.1000⁃3428.2015.07.052

河南省科技攻关计划基金资助项目（122102210430）。

魏长宝（1972-），男，副教授、硕士，主研方向：图像处理，智能信息处理；姚汝贤，副教授、硕士。

2014⁃12⁃24

2015⁃02⁃07E⁃mail：82671778＠qq.com