毕达哥拉斯模糊软集及其应用

彭新东，杨 勇，宋娟萍，蒋 芸

（西北师范大学计算机科学与工程学院，兰州730070）

·人工智能及识别技术·

毕达哥拉斯模糊软集及其应用

彭新东，杨 勇，宋娟萍，蒋 芸

（西北师范大学计算机科学与工程学院，兰州730070）

直觉模糊软集不能处理参数的隶属度与非隶属度之和大于1的情况，使决策过程受限，影响其应用范围。针对该问题，结合毕达哥拉斯模糊集的特性与软集的参数化，构造毕达哥拉斯模糊软集。介绍毕达哥拉斯模糊软集的补、并、交、且、或、加、乘、必须、可能等运算，给出运算结果，并讨论其德摩根定律。设计基于毕达哥拉斯模糊整合算子的决策算法，分析该算法的计算复杂度，并将其应用到股票投资，应用结果证明了该算法的有效性。

毕达哥拉斯模糊软集；整合算子；德摩根定律；计算复杂度；股票投资

中文引用格式：彭新东，杨 勇，宋娟萍，等.毕达哥拉斯模糊软集及其应用［J］.计算机工程，2015，41（7）：224⁃229.

英文引用格式：Peng Xindong，Yang Yong，Song Juanping，et al.Pythagorean Fuzzy Soft Set and Its Application［J］.Computer Engineering，2015，41（7）：224⁃229.

1 概述

Molodstov于1999年从参数化的角度提出了一种新的处理不确定性问题的数学工具，即软集［1］，并成功地将其应用到函数的平滑化、黎曼积分、测度论等数学分支中。

近年来，许多学者将软集理论与其他数学模型相结合。Maji等在2001年将模糊集与软集结合，提出了模糊软集［2］，讨论了相应的一些性质，随后其提出了直觉模糊软集［3］。2010年，文献［4］将模糊软集应用到文本分类；2013年，Yang等提出了多模糊软集［5］，并将其应用到决策；结合双极模糊集［6］的概念，Yang等又提出了一个应用更广的模型，即双极多模糊软集［7］。为了解决模糊软集信息随时间动态变化的情形，文献［8］提出时序模糊软集。文献［9］基于时序模糊软集给出一个新的多属性群决策算法。

由于直觉模糊软集不能描述参数的隶属度与非隶属度之和大于1的情况，使得决策过程受到很大限制，影响了其应用范围。因此，本文结合毕达哥拉斯模糊集［10⁃11］与软集，提出毕达哥拉斯模糊软集，允许参数中的隶属度与非隶属度之和大于1，但其平方和小于1，是直觉模糊软集的一种推广，并将其应用于股票投资中。

2 预备知识

定义1 设U为初始论域，E为参数集，P（U）为U的幂集，A⊆E，F：A→P（U），称（F，A）为U上的一个软集［1］。

定义2 设U为一个论域，U上形如I＝｛＜x， μI（x），的三元组称为U上的一个直觉模糊集。 其中，μI∈［0，1］，νI∈［0，1］，且 μI+ νI≤1。 为了方便，记（μI，νI）为一个直觉模糊数（Intuitionistic Fuzzy Number，IFN）［12］。

定义3 设U为初始论域，E为非空参数集，为I（U）的所有直觉模糊集的全体，A⊆E，F：A→H（U），称（F，A）为U上的一个直觉模糊软集［3］。

定义4 设U为一个论域，U上形如P＝｛＜x，μP（x），νP（x）＞｜x∈U｝的三元组称为U上的一个毕达哥拉斯模糊集。其中，μP∈［0，1］，νP∈［0，1］，且。为了方便，记（μP，νP）为一个毕达哥拉斯模糊数（Pythagorean Fuzzy Number，PFN）［13］。

易知毕达哥拉斯模糊数的隶属空间比直觉模糊数大，如图1所示［10］。

图1 PFN与IFN的隶属空间大小比较

定义5 给定毕达哥拉斯模糊数p，p1，p2，相应的运算式为［10⁃11，13］：

定理1 设p，p1，p2为毕达哥拉斯模糊数，λ＞0，λ1＞0， λ2＞0，则［10⁃11，13］：λ2

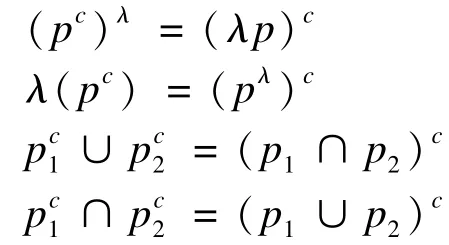
定义6 设p＝（μp，νp）是一个毕达哥拉斯模糊数，其得分函数为［13］：

其中，s（p）∈［-1，1］。对任意的2个毕达哥拉斯模糊数p1，p2，如果 s（p1） ＞s（p2），则 p1≻p2；如果s（p1）＝s（p2），则 p1～p2，且≻，～表示优于、相等运算。

3 毕达哥拉斯模糊软集及其运算

3.1 毕达哥拉斯模糊软集

定义7 设 U是一个集合，E是一个参数集，PFU表示U上所有毕达哥拉斯模糊集的全体，A⊆E，F：A→PFU是一个映射，则称（F，A）是U上的一个毕达哥拉斯模糊软集。

一个U上的毕达哥拉斯模糊软集就是U上的一些毕达哥拉斯模糊子集构成的参数族。对于任意参数e∈A，F（e）是一个与e相关的毕达哥拉斯模糊软集，可记为F（e）＝｛＜x，μp（x），νp（x）＞｜x∈U｝。

在实际决策过程中，相对于直觉模糊软集，毕达哥拉斯模糊软集描述的隶属空间更大。克服了直觉模糊软集参数的隶属度与非隶属度之和大于1的情况不能有效描述的缺陷，因此，其有更强的应用能力。

例1 设U＝｛x1，x2，x3｝代表3幅国画的集合，A是参数集合，且A＝｛e1，e2，e3｝＝｛个人风格，审美心理，技巧难度｝。毕达哥拉斯模糊软集（F，A）如下：

定义8 设U是一个集合，E是一个参数集，A，B⊆E，（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，若（F，A）和（G，B）满足下列2个条件：

（1）A⊇B；

（2）∀e∈B，x∈U，μA（x）≥μB（x），νA（x）≤νB（x）。

例2 设U上的毕达哥拉斯模糊软集（G，B）如例1中定义，B＝｛e1｝，则毕达哥拉斯模糊软集（G，B）定义如下：

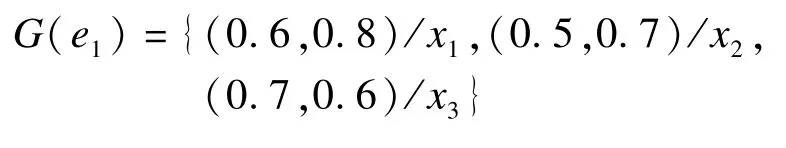
定义9 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，若且，则称（F，A）和（G，B）是毕达哥拉斯模糊软相等，记为

定义10 设（F，A）是U上的毕达哥拉斯模糊软集，若∀e∈A，F（e）＝｛（1，0）｝，则称（F，A）是满毕达哥拉斯模糊软集，记为UA；若∀e∈A，F（e）＝｛（0，1）｝，则称（F，A）是空毕达哥拉斯软集，记为ΦA。

3.2 毕达哥拉斯模糊软集运算

定义11 设（F，A）是U上的毕达哥拉斯模糊软集，映射F：A→PFU；Fc（e）＝（F（e））c（∀e∈A），则称（Fc，A）为毕达哥拉斯模糊软集的补，记为（F，A）c。

值得注意的是（F，A）c的参数集仍然为A，而不是¬A。

例3 设U上的毕达哥拉斯模糊软集（G，B）如例2中定义，则 Gc（e1）＝｛（0.8，0.6）／x1，（0.7，0.5）／x2，（0.6，0.7）／x3｝。

定义12 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，则（F，A）和（G，B）上的“且”记为（F，A）∧（G，B）＝（H，A×B），对∀（α，β）∈A×B，x∈U，H（α，β）＝（min（μa，μβ），max（να，νβ））。

定义13 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，则（F，A）和（G，B）上的“或”记为（F，A）∨（G，B）＝（O，A×B），对∀（α，β）∈A×B，x∈U，O（α，β）＝（max（μa，μβ），min（να，νβ））。

例4 设U上的毕达哥拉斯模糊软集（G，B）定义为B＝｛e1，e2｝，则毕达哥拉斯模糊软集（G，B）定义如下：

例5 结合例1与例4，则（F，A）和（G，B）上的“且”，“或”运算的结果如表1、表2所示。

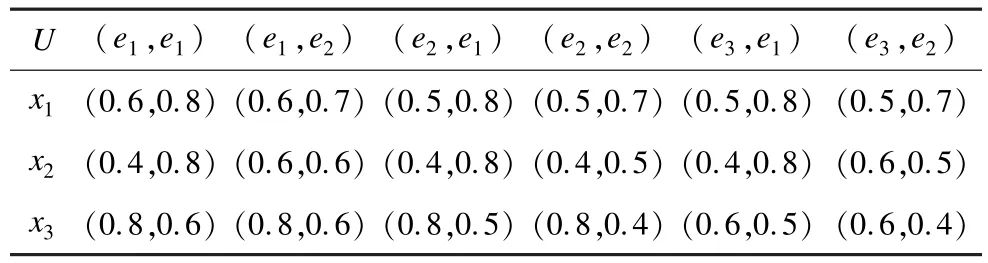
表1 （F，A）和（G，B）上“且”运算后的结果

表2 （F，A）和（G，B）上“或”运算后的结果

定理2 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，则：

另一个公式的证明与其类似。

定义14 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，若C＝A∪B，且对∀e∈C，有以下公式：

定义15 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，若C＝A∩B，且对∀e∈C，H（e）＝F（e）∩G（e），则称（H，C）是（F，A）和（G，B）的“交”，记为

例6 结合例1与例4，则（F，A）和（G，B）上的“并”，“交”运算的结果如表3、表4所示。

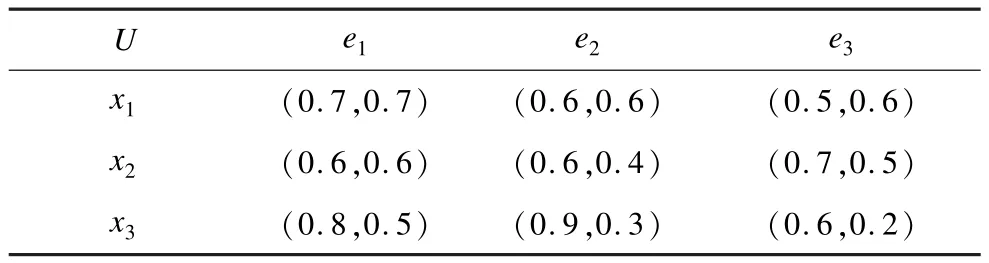
表3 （F，A）和（G，B）上“并”运算后的结果

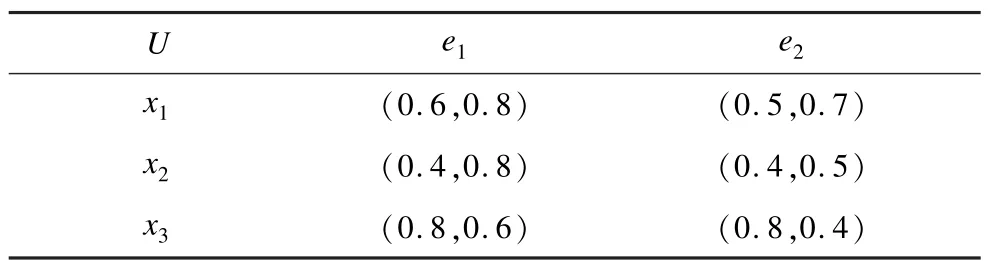
表4 （F，A）和（G，B）上“交”运算后的结果

定理3 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，则：

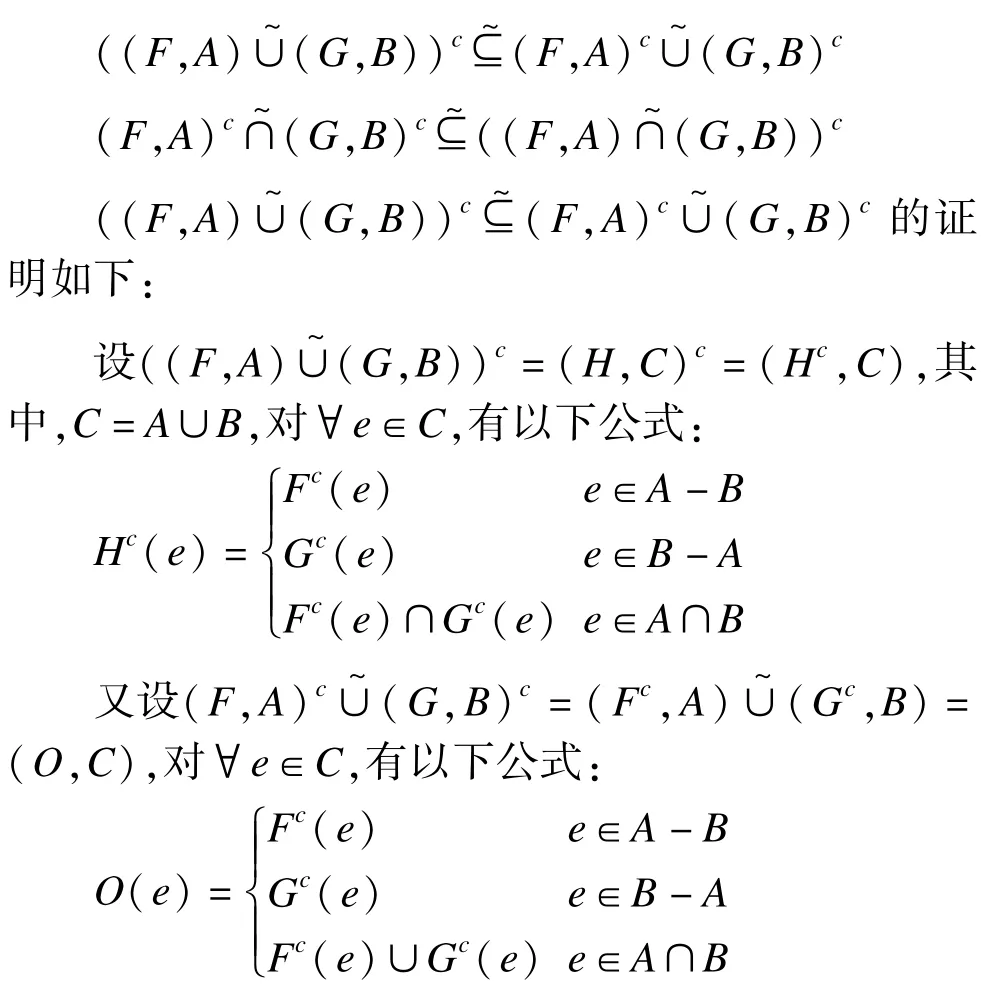
由此可知，Hc（e）⊆～O（e），故原式得证。

另一个公式的证明与其类似。

定义16 设（F，A）是U上的毕达哥拉斯模糊软集，毕达哥拉斯模糊软集（F，A）λ（λ＞0）定义如下：

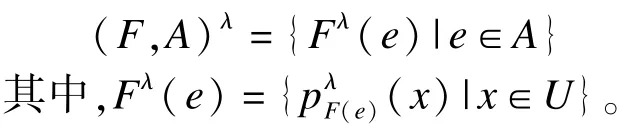
定义17 设（F，A）是U上的毕达哥拉斯模糊软集，毕达哥拉斯模糊软集λ（F，A）（λ＞0）定义如下：

λ（F，A）＝｛λF（e）｜e∈A｝

其中，λF（e）＝｛λpF（e）（x）｜x∈U｝。

定理4 设（F，A）是U上的毕达哥拉斯模糊软集，λ＞0，则：

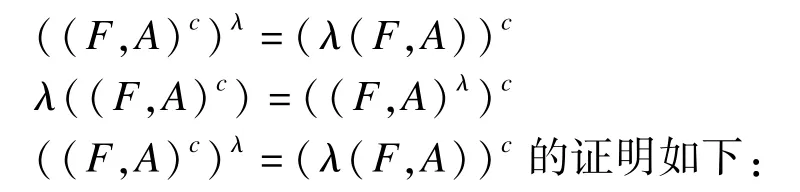
∀e∈A，根据命题，可得（Fc（e））λ＝（λF（e））c。进而（（F，A）c）λ＝（λ（F，A））c。

另一个公式的证明与其类似。

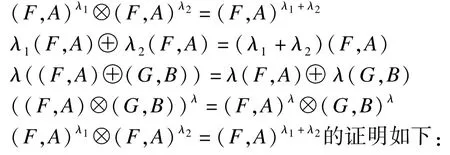
定理5 设（F，A），（G，B）是U上的毕达哥拉斯模糊软集，λ＞0，λ1＞0，λ2＞0，则：∀e∈A，根据命题，可得 Fλ1（e）⊗Fλ2（e）＝Fλ1+λ2（e）。 进而（F，A）λ1⊗（F，A）λ2＝（F，A）λ1+λ2。

其余公式的证明与其类似。

定义18 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，则（F，A）和（G，B）的“加”运算定义如下：

其中，对∀（α，β）∈A×B，H（α，β）＝F（α）⊕G（β）。

定义19 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，则（F，A）和（G，B）的“乘”运算定义如下：

其中，对∀（α，β）∈A×B，O（α，β）＝F（α）⊗G（β）。

例7 结合例1与例4，则（F，A）和（G，B）上的“加”，“乘”运算结果如表5、表6所示。

表5 （F，A）和（G，B）上“加”运算后的结果

表6 （F，A）和（G，B）上“乘”运算后的结果

定理6 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，则：

设（F，A）⊕（G，B） ＝（H，A ×B），因此，（（F，A）⊕（G，B））c＝（H，A×B）c＝（Hc，A×B），（F，A）c⊗（G，B）c＝ （Fc，A）⊗（Gc，B）＝（O，A× B），对∀（α，β）∈A×B，根据命题可知，Hc（α，β）＝（F（α）⊕G（β））c＝Fc（α）⊗Gc（β），又 O（α，β） ＝Fc（α）⊗Gc（β），因此，Hc（α，β）＝O（α，β）。 故原式得证。

另一个公式的证明与其类似。

定义20 设（F，A）是U上的毕达哥拉斯模糊软集，则（F，A）的“必须”运算定义如下：

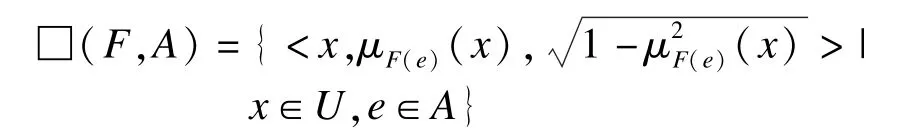
定义21 设（F，A）是U上的毕达哥拉斯模糊软集，则（F，A）的“可能”运算定义如下：

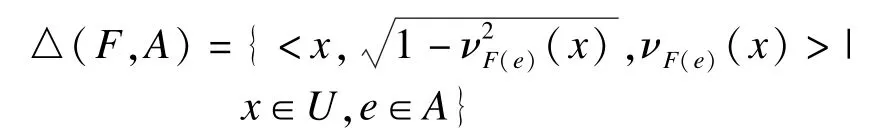
定理7 设（F，A）和（G，B）是U上的毕达哥拉斯模糊软集，则：

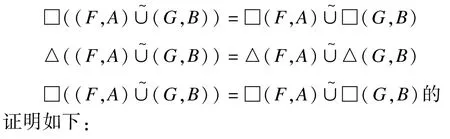
设（F，A）∪～（G，B）＝（H，C），其中，C＝A∪B，对∀e∈C，有以下公式：

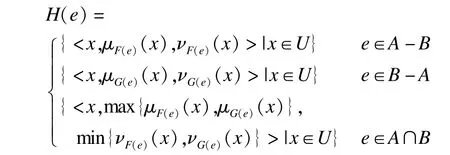
然后，□（（F，A）∪～（G，B））＝□（H，C），根据定义20得：

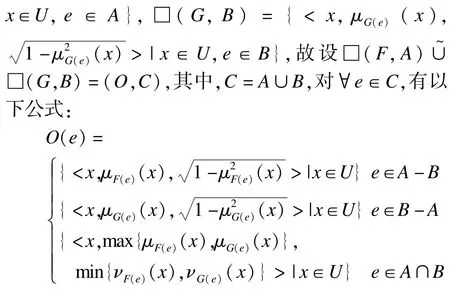
易知□（H，C）与（O，C）是同一个毕达哥拉斯模糊软集，因此，原式得证。

另一个公式的证明与其类似。

4 基于毕达哥拉斯整合算子的决策算法

对于一个毕达哥拉斯模糊软信息的决策问题，设U＝｛x1，x2，…，xm｝是一系列对象，A＝｛e1，e2，…，en｝是一系列参数。决策者提供了对象 xi（i＝1，2，…，m）在参数ei（i＝1，2，…，n）下的毕达哥拉斯模糊数的值为pij＝（μij，νij），可以构造一个毕达哥拉斯模糊软决策矩阵 P＝｛pij｝m×n，其中，pij（i＝1，2，…，m；j＝1，2，…，n）。

基于毕达哥拉斯整合算子的决策算法如下：

输入 毕达哥拉斯模糊软集（F，A）与权重向量w

输出 最优对象xi

Step1 通过文献［10⁃11］的毕达哥拉斯模糊加权平均（Pythagorean Fuzzy Weighted Average，PFWA）算子可以获得对象xi整合后的毕达哥拉斯数pi：

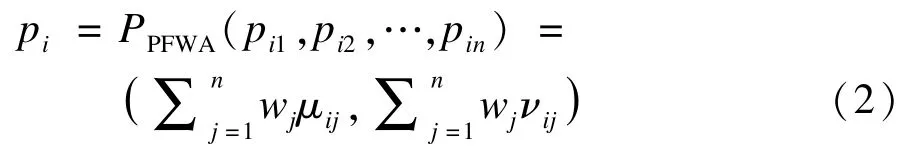
Step2 通过式（1）计算每个对象 xi的得分函数s（pi）。

Step3 选择最优的对象xi，当且仅当maix s（pi）。

对于该决策算法的计算复杂度（C）可以分为计算对象的毕达哥拉斯数（C1）、计算得分函数（C2）、计算相应的排序（C3）。

假设无论经过什么运算都算一个计算量，排序一次也算一个计算量，因此：

（1）对于每个对象xi（i＝1，2，…，m）的计算量为相应隶属度与非隶属度整合运算的次数之和，即C1＝2m。

（2）得分函数的计算复杂度为C2＝m。

（3）计算排序的复杂度可分为最好与最坏2种情况，采用快速排序算法，对于最好的情况复杂度为C31＝m lb m，对于最坏的情况复杂度为C32＝m2。

综合上述，可知该算法的计算复杂度为 C1+ C2+C31＝3m+m lb m≤C≤3m+m2＝C1+C2+C32。

5 应用实例

设有5只市盈率比较高的互联网股票集合U＝｛x1，x2，x3，x4，x5｝，A是 4个评判标准集合且A＝｛e1，e2，e3，e4｝＝｛大盘趋势，政策导向，年报业绩，流通市值｝。毕达哥拉斯模糊软集如表7所示。

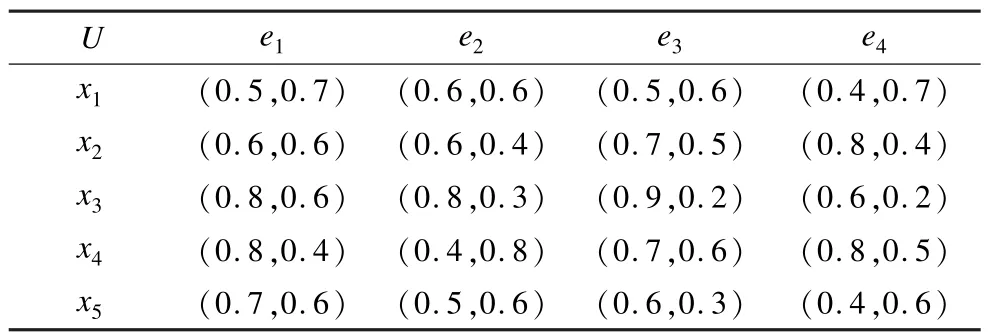
表7 毕达哥拉斯模糊软集（F，A）

设一位资深股民想选择一只股票进行投资，对每个影响股票的参数ei（i＝1，2，3，4）赋予相应的权重w1＝0.2，w2＝0.3，w3＝0.4，w4＝0.1。

根据式（2），可以计算出每个对象xi经整合后的毕达哥拉斯数 pi，p1＝（0.52，0.63），p2＝（0.66，0.48），p3＝（0.82，0.31）。p4＝（0.64，0.61），p5＝（0.57，0.48）再通过式（1）计算每个对象xi的得分函数为，s（p1）＝-0.126 5，s（p2）＝0.205 2，s（p3）＝0.576 3，s（p4）＝0.037 5，s（p5）＝0.094 5。

很明显，s（p3） ＞ s（p2） ＞ s（p5） ＞ s（p4） ＞s（p1），因此，该股民会选择股票x3进行投资。

6 结束语

本文结合毕达哥拉斯模糊集与软集，提出毕达哥拉斯模糊软集，并给出毕达哥拉斯模糊软集的运算方法，讨论其性质，设计基于毕达哥拉斯整合算子的决策算法。实例结果证明了该算法的有效性。下一步将探讨毕达哥拉斯模糊软集的信息测度（距离测度、相似度、包含度、子集度、熵测度）的公理化定义，研究相应的信息测度公式，并将其应用到专家的聚类分析中。

［1］ Molodtsov D A.Soft Set Theory⁃first Results［J］.Computers and Mathematics w ith Applications，1999，37（4）：19⁃31.

［2］ Maji PK，Biswas R，Roy A R.Fuzzy Soft Set［J］.Journal of Fuzzy Mathematics，2001，9（3）：589⁃602.

［3］ Maji P K，Biswas R，Roy A R.Intuitionistic Fuzzy Soft Set［J］.Journal of Fuzzy Mathematics，2001，9（3）：677⁃692.

［4］ 洪智勇，秦克云.基于模糊软集理论的文本分类方法［J］.计算机工程，2010，36（13）：90⁃92.

［5］ Yang Yong，Tan Xia，Meng Congcong.The Multi⁃fuzzy Soft Set and Its Application in Decision Making［J］.Applied Mathematical Modelling，2013，37（7）：4915⁃4923.

［6］ Lee K M.Bipolar⁃valued Fuzzy Sets and Their Basic Operations［C］／／Proceedings of International Conference.Berlin，Germany：Springer⁃Verlag，2000：307⁃317.

［7］ Yang Yong，Peng Xindong，Chen Hao，et al.A Decision Making Approach Based on Bipolar Multi⁃fuzzy Soft Set Theory［J］.Journal of Intelligent and Fuzzy Systems，2014，27（4）：1861⁃1872.

［8］ 毛军军，姚登宝，王翠翠，等.基于时序模糊软集的群决策方法［J］.系统工程理论与实践，2014，34（1）：182⁃189.

［9］ 钱庆庆，吴 涛，宋 雷，等.基于时序模糊软集的群决策新方法［J］.重庆理工大学学报：自然科学版，2014，28（10）：126⁃130.

［10］ Yager R R.Pythagorean Membership Grades in Multicri⁃teria Decision Making［J］.IEEE Transactions on Fuzzy Systems，2014，22（4）：958⁃965.

［11］ Yager R R，Abbasov A M.Pythagorean Membership Grades，Complex Numbers，and Decision Making［J］.International Journal of Intelligent Systems，2013，28（5）：436⁃452.

［12］ Atanassov K.Intuitionistic Fuzzy Sets［J］.Fuzzy Sets and Systems，1986，20（1）：87⁃96.

［13］ Zhang Xiaolu，Xu Zeshui.Extension of TOPSIS to Multiple Criteria Decision Making with Pythagorean Fuzzy Sets［J］.International Journal of Intelligent Systems，2014，29（12）：1061⁃1078.

编辑 刘 冰

Pythagorean Fuzzy Soft Set and Its Application

PENG Xindong，YANG Yong，SONG Juanping，JIANG Yun
（College of Computer Science and Engineering，Northwest Normal University，Lanzhou 730070，China）

In order to solve the problem that intuitionistic fuzzy soft set can not deal w ith the situation that the sum of membership degree and non⁃membership degree of the parameter is bigger than 1.Itmakes the decision processs lim ted，and affects the application range.This paper combines the characteristics of Pythagorean fuzzy set w ith the parameterization of soft set，and constructs Pythagorean fuzzy soft set.Some operations such as complement，union，intersection，and，or，addition，multiplication，necessity，and possibility are defined.Some corresponding results are presented，and the De Morgan’s Law of Pythagorean fuzzy soft sets are discussed in detail.A decision making algorithm based Pythagorean fuzzy aggregation operator is proposed.This paper analyses the computational complexity of this algorithm，and applies it to stock investment.Experimental results show that the algorithm is effectiveness.

Pythagorean fuzzy soft set；aggregation operator；De Morgan’s law；computational complexity；stock investment

1000⁃3428（2015）07⁃0224⁃06

A

TP301

10.3969／j.issn.1000⁃3428.2015.07.043

国家自然科学基金资助项目（61163036）。

彭新东（1990-），男，硕士研究生，主研方向：决策支持系统，专家系统；杨 勇（通讯作者），教授、博士；宋娟萍，硕士研究生；蒋 芸，教授、博士。

2014⁃11⁃28

2014⁃12⁃22E⁃mail：yangzt＠nwnu.edu.cn