前轮主销间隙对汽车蛇行工况下稳定性的影响
2015-08-19蒋亦斌魏道高王鹏潘之杰肖怀阳
蒋亦斌+魏道高+王鹏+潘之杰+肖怀阳

摘 要:主销间隙是影响汽车蛇行工况下稳定性的重要参数。将转向机构简化为平面连杆机构,并就机构中转向节主销与衬套间隙对蛇形工况下汽车稳定性的影响进行分析。考虑以上间隙建立了四自由度车辆操纵运动系统数学模型,基于该模型,应用数值分析方法对间隙参数变化时样车质心侧偏角的稳定性进行仿真分析。结果表明,间隙参数变化时车辆蛇行动力学行为表现为由倍周期进入单周期、混沌,然后从倍周期回到单周期。随着间隙的增大,汽车蛇行失稳的上临界频率几乎无变化,但下临界频率逐渐加大,失稳频率带宽也相应加大,且混沌区域的窗口动力学特性有明显差异。
关键词:主销间隙;平面连杆机构;蛇行;动力学行为;混沌
中图分类号:U463.46文献标文献标识码:A文献标DOI:10.3969/j.issn.2095-1469.2015.03.06
蛇行工况是汽车行驶过程中一种常见工况,在道路交通中时有事故出现[1-3],因此国内外学者对其展开较广泛而深入的研究。文献[4]运用VEDYNA建立了样车模型,并运用硬件在环试验进行了蛇形工况仿真,分析了汽车质心位置对蛇行工况稳定性的影响,得出过高的质心位置会使汽车运动稳定性变差,使其可能在蛇行行驶工况时发生侧翻。文献[5]建立了电动轮独立驱动汽车的多自由度系统模型,通过变速度的汽车蛇行工况试验,分析得出了行驶速度对汽车蛇行工况行驶稳定性的影响。文献[6]建立了二自由度汽车系统模型,进行了不同幅值的转向盘正弦输入仿真试验,通过相平面分析,得出过高的正弦转向幅值会使汽车蛇行工况行驶稳定性变差。文献[7]建立了二自由度汽车系统模型,进行了不同周期的转向盘正弦输入仿真试验,得出了转向盘正弦输入频率对汽车蛇行工况行驶稳定性有较大的影响。文献[8]建立了多自由度的汽车路面系统模型,分别对二自由度、三自由度及四自由度系统模型进行蛇行工况仿真试验,对比样车道路试验结果,得到了三自由度及四自由度汽车路面系统模型能更好地反映汽车蛇形工况的结论。文献[9]建立了考虑四轮定位参数的汽车四自由度操纵稳定性模型,运用数值仿真分析,得到了四轮定位参数对汽车蛇行工况稳定性的影响。文献[10]~[12]针对不同的汽车系统模型,提出了多种汽车行驶稳定性控制策略,通过蛇行工况仿真试验,证明这些针对车轮滑移率、质心侧偏角及横摆角速度的控制策略能够有效地提高汽车蛇行工况行驶稳定性。
综上分析可见,以上学者的研究多是关于工况参数(如行驶速度v和方向盘转向角δ)、汽车质心位置及控制策略对蛇行稳定性的影响,而转向系间隙对汽车蛇行工况频率特性的影响未被重视,正如文献[13]写道:“至今很难见到论述转向系间隙影响汽车操纵运动文献”。而我们前期研究表明间隙对操纵运动的影响不可忽略[14]。
因此,本文在以上学者研究成果以及我们前期研究的基础上,考虑转向节主销与衬套间隙非线性因素,建立了含车身侧倾运动的四自由度汽车转向行驶非线性动力学模型。对该模型进行数值计算与分析,以获得转向节主销与衬套间隙因素对汽车蛇行工况下频率特性的影响,寻找间隙影响蛇行稳定性的规律,进一步丰富汽车转向行驶工况非线性动力学理论。
1 含主销间隙转向行驶系统动力学模型
1.1 考虑间隙的系统力学模型
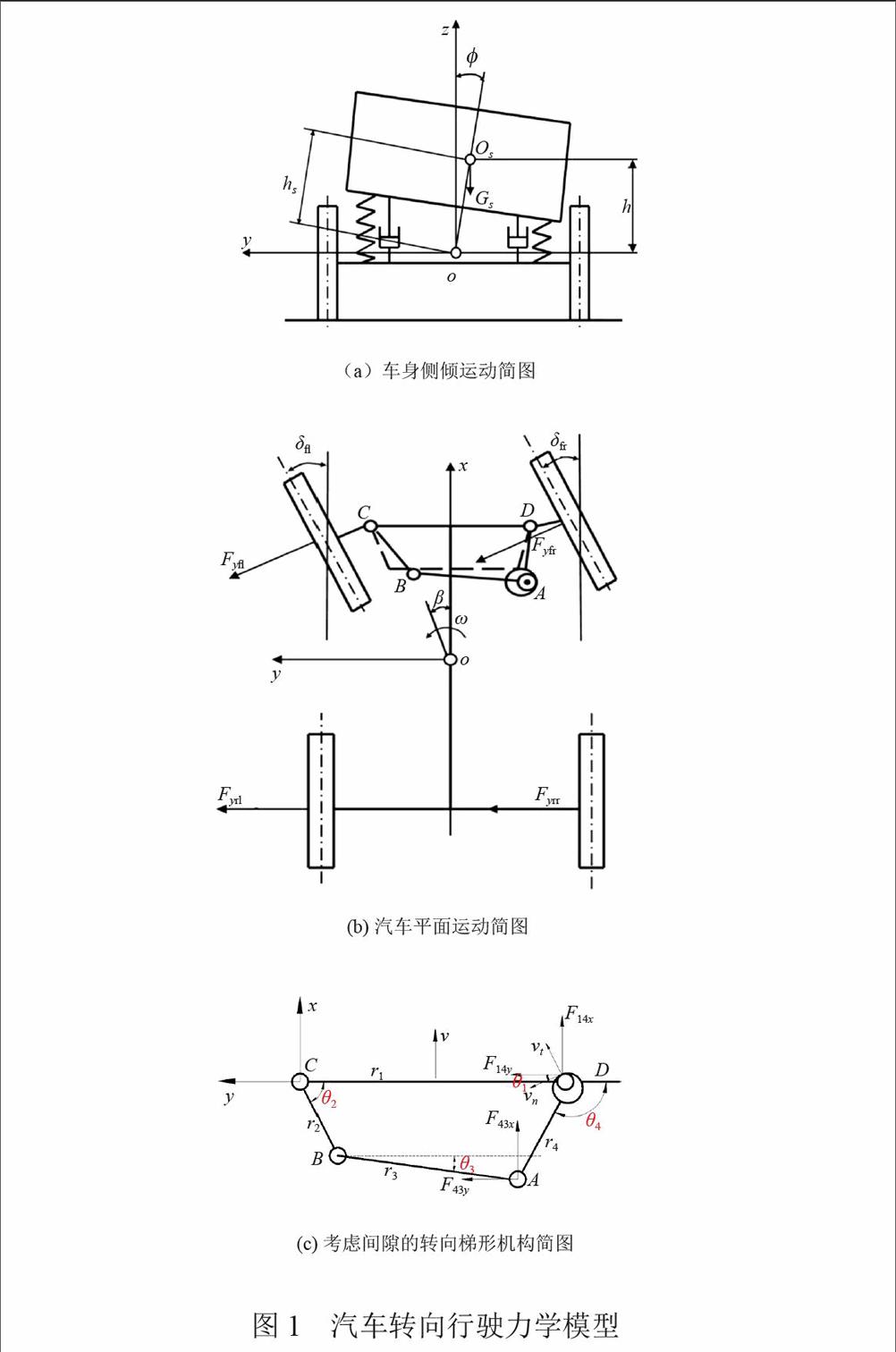
在前人建立的汽车转向行驶系统力学模型的基础上,本文考虑转向节主销与衬套间隙对转向稳定性的影响,建立样车转向系统力学模型和坐标系如图1(a)、(b)、(c)所示。
由于考虑主销间隙,忽略前轮定位参数影响,将样车的转向梯形机构简化为曲柄连杆机构[15-16],如图1(c)所示。为简化分析过程仅考虑转向节主销与衬套间隙,杆件均看作刚体。汽车以速度v做等速蛇行行驶,oxyz为固定于侧倾中心的坐标系,xoy与路面平行,x轴指向汽车行驶方向,z轴铅垂向上,y轴按右手定则指向左侧。
该系统力学模型做如下假设:
(1)不计空气阻力。(2)忽略前轮定位参数影响,转向梯形机构与xoy坐标平面平行。(3)车辆前后悬架侧倾中心相同。
汽车转向行驶系统,用4个自由度表示:横摆角速度ω,质心侧偏角β,车身侧倾角,左前轮转向角δl。
1.2 含主销间隙车辆转向行驶运动微分方程
根据图1(a)、(b)、(c)车辆转向行驶力学模型,运用达朗贝尔定理,建立车辆转向行驶整车运动微分方程。
1.2.1 车辆转向行驶运动方程
(1)整车绕z轴力矩平衡方程
(2)整车沿y轴力平衡方程
。
(3)车身绕x轴侧倾力矩平衡方程
。
(4)前从动轮(右)绕主销的力矩平衡方程
。
式中,Fyfl为左前轮侧偏力,N;Fyfr为右前轮侧偏力,N;Fyrl为左后轮侧偏力,N;Fyrr为右后轮侧偏力,N;δr为右前轮转角,rad;lf为前轴距,m;lr为后轴距,m;m为整车质量,kg;ms为簧上质量,kg;hs簧上质量质心到侧倾轴线距离,m;Ix为簧上质量绕x轴转动惯量,kg·m2;Ixz为簧上质量绕x、z两轴惯性积,kg·m2;Iz为整车绕z轴转动惯量,kg·m2; Cφ为车身侧倾角阻尼,N·m·s /rad;kφ为车身侧倾角刚度,N·m/rad;Jc为右梯形臂绕右侧主销的转动惯量,kg·m2;Dw为回正力臂,m;MP间隙对主销碰撞力矩,N·m;为右梯形臂的转动角加速度,rad/s2。
1.2.2 轮胎侧向力表达式
(1)汽车轮胎侧向力选用文献[17]简化的魔术公式
。
其中
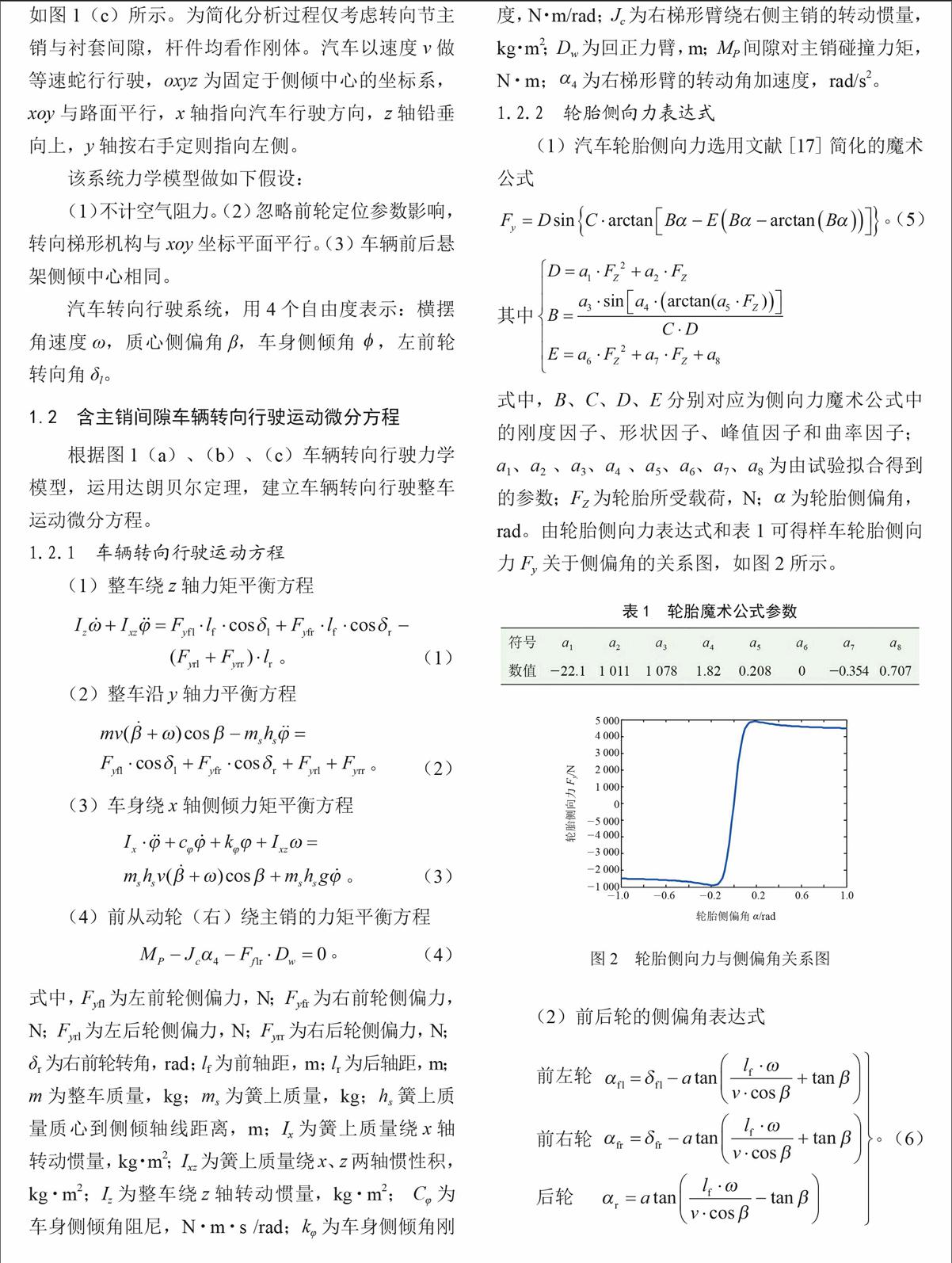
式中,B、C、D、E分别对应为侧向力魔术公式中的刚度因子、形状因子、峰值因子和曲率因子;a1、a2 、a3、a4 、a5、a6、a7、a8为由试验拟合得到的参数;FZ为轮胎所受载荷,N;为轮胎侧偏角,rad。由轮胎侧向力表达式和表1可得样车轮胎侧向力Fy关于侧偏角的关系图,如图2所示。
(2)前后轮的侧偏角表达式
(3)车辆转向行驶时,左右车轮载荷转移表达式
前桥左轮载荷
前桥右轮载荷
后桥左轮载荷
后桥右轮载荷
1.2.3 转向梯形间隙碰撞力矩求解
根据图1(c)车辆转向行驶时转向梯形机构简化力学模型,求解转向节主销与衬套间隙碰撞力矩。图1(c)中的右球头间隙碰撞模型选用二状态间隙碰撞模型,设间隙e沿x、y轴的分量分别为ex、ey,汽车直线行驶时转向梯形底角为。由其几何关系可得:
。
式中,;;,
r1为左右主销之间的水平距离;r2为左转向梯形臂长度,m;r3为右转向梯形臂长度,m;r4为横拉杆长度,m;2、3、4分别为左梯形臂、横拉杆、右梯形臂和y轴所成的角度,rad。
设接触角1由下式表示:
设间隙中轴销相对于轴套的法向速度和切向速度分别为vn、vt。
。
引入符号函数
间隙运动副碰撞力法向力Fn与切向力Ft分别为
。
式中,;K为间隙处轴套表面刚度,
N/m;f为间隙处轴套表面摩擦系数;r为间隙,m; Cn为间隙处轴套表面法向阻尼系数,N·s/m;Ct为间隙处轴套表面切向阻尼系数,N·s/m。
引入阶跃函数
式(16)在x、y方向的分量为
。
由其可得主销与衬套间隙对主销的碰撞力矩
。
式中,R为轴销半径,m。
2 主销间隙对蛇行频率特性影响的计算分析
以国产某型轿车为样车,运用以上数学模型采用数值计算方法[18-19]对间隙影响样车蛇行工况稳定性进行仿真分析,计算所需的样车参数见表2。
2.1 间隙C对蛇行频率特性影响
根据表2中样车参数对其转向梯形机构[图1(c)]主销间隙C分别取0,0.5,1,1.5,2,2.5,3 mm,取速度v为20 m/s,进行数值计算,寻找间隙对车辆蛇行工况频率特性影响规律。蛇行工况下车辆质心侧偏角频率特性如图3所示。并且对图3(a)、(b)、(c)、(d)、(e)、(f)、(g)中取f=2.6 rad/s时相图做相应的庞加莱映射和功率谱图进行分析,结果如图4所示。
图3为不同主销间隙(C=0,0.5,1,1.5,2,2.5,3 mm)时,车辆蛇行工况下,质心侧偏角频率特性分叉图。表3为不同间隙车辆失稳时质心侧偏角的上下临界频率及带宽。间隙C取不同值时车辆蛇行工况一致性表现为由倍周期走向单周期,然后单周期走向混沌、倍周期,最后又回到单周期运动。但是不同间隙时,转向蛇行工况质心侧偏角随转向角频率失稳的上下临界频率不同,且失稳频率带宽随间隙增大而增大。由图3及表3可见,当C=0~1.0 mm范围时,分叉频率带宽较小,理论上说明在设计转向节主销与衬套间隙C<1.0 mm范围有利于减小车辆蛇行失稳的几率。
由此可见,随着间隙C增加,汽车蛇行失稳的上临界频率几乎无变化,而失稳的下临界频率逐渐加大,由其导致蛇形行驶失稳的频率带宽相应加大,说明转向节主销与衬套间隙过大,增加了车辆蛇行失稳的概率。但是通过以上数值计算,可以找到理论上减小车辆失稳的主销与衬套间隙的较好区间(0,1.0) mm,能为设计与制造优选主销间隙提供理论参考。
2.2 对图3质心侧偏角频率特性的相图分析
在图3(a)、(b)、(c)、(d)、(e)、(f)、(g)分叉图中有一个共同特点,样车作蛇行行驶时,在f=2.6 rad/s处的分叉行为较复杂。因此对图3统一取f=2.6 rad/s处做进一步细化,对质心侧偏角的动力学行为作车辆蛇形频率特性分析,车辆在该转向频率时,质心侧偏角相图、庞加莱映射及功率谱图如图4(a)、(b)、(c)、(d)、(e)、(f)、(g)所示。
图4为图3中f=2.6 rad/s时,的相图、庞加莱图及其功率谱图。由图4可见,当f=2.6 rad/s时,随着间隙C增大,车辆质心侧偏角分叉行为表现为由三倍周期走向混沌,但在C<1.0 mm时,系统周期解稳定性较好。主销间隙C>1.0 mm后整车蛇形工况的动力学行为表现为混沌,车辆失稳行为表现得更加复杂。由此可能致使车辆在紧急工况下驾驶员急打方向盘而导致汽车甩尾、侧翻事故。因此,为了安全,应及时检查旧车转向节主销与衬套间隙是否超值,保证合理的安全间隙。对于产品设计,应该从车辆蛇行工况安全的角度合理选取转向节主销与衬套间隙。
3 结论
(1)考虑前轮主销间隙建立了汽车转向行驶四自由度系统动力学模型。
(2)通过对样车前轮主销间隙C取不同值时的数值计算,从质心侧偏角频率特性分叉图及其相图、庞加莱图、功率谱图发现,随主销间隙增加,整车系统一致性地表现为由倍周期进入单周期、混沌,然后从倍周期回到单周期。随间隙C增加,车辆蛇行行驶失稳的上临界频率几乎无变化,但失稳的下临界频率逐渐加大,失稳的带宽相应加大,说明间隙C增加对车辆蛇形稳定性不利。理论上找到C<1.0 mm区间时车辆蛇行工况失稳区间较小,这一范围在设计和制造上也易于实现。
(3)主销间隙对车辆蛇行失稳的影响趋势以及寻找到的有利于车辆蛇形稳定性的区间,能为车辆转向桥设计提供理论参考。
参考文献(References):
Ren Yuanyuan,Zheng Xuelian,Li Xiansheng. Handling Stability of Tractor Semitrailer Based on Handling Diagram [J]. Discrete Dynamics in Nature and Society,2012,37(10):1887-1991.
BLACK J,WAGNER J,ALEXANDER K,et al. Vehicle Road Runoff-Active Steering Control for Shoulder Induced Accidents[C]//American Control Conference,Seattle,WA,2008:3237-3244.
JONES I S. The Use of Accident Data in Studying Vehicle Handling Performance[C]//Proceedings of the Institution of Mechanical Engineers,1975:243-258.
CHUCHOLOWSKI C,V?GEL M,VON STRYK O,et al. Real Time Simulation and Online Control for Virtual Test Drives of Cars. High Performance Scientific and Engineering Computing [C]//Lecture Notes in Computational Science and Engineering,Springer,1999:1-10.
王军年.电动轮独立驱动汽车差动助力转向技术研究 [D]. 长春:吉林大学, 2009.
Wang Junnian.Study on Differential Drive Assist Steering Technology for Electric Vehicle with Independent-Motorized-Wheel-Drive [D]. Changchun:Jilin University,2009.(in Chinese)
刘丽.车辆三自由度平面运动稳定性的非线性分析及控制策略评价 [D]. 长春:吉林大学,2010.
Liu Li. Nonlinear Analysis and Control Strategy Evaluation on the Stability of Vehicle 3-DOF Planar Motion[D]. Changchun:Jilin University, 2010.(in Chinese)
杨秀建.极限工况下周期转向汽车侧向动力稳定性及分岔分析 [J]. 公路交通科技, 2009, 26(11):141-152.
Yang Xiujian. Analysison Lateral Dynamic Stability and Bifurcation of Vehicle Periodic Steering under Critical Condition [J]. Journal of Highway and Transportation Research and Development, 2009,26(11):141-152.(in Chinese)
KIM J. Effect of Vehicle Model on the Estimation of Lateral Vehicle Dynamics [J]. International Journal of Automotive Technology,2010,11(3):331-337.
肖怀阳. 四轮定位参数对蛇形工况下汽车频率特性影响研究 [D].合肥:合肥工业大学, 2012.
Xiao Huaiyang. A Study on the Influence of Four Wheel Alignment Parameter at Frequency Characteristics on Vehicle Stability on Snake-Like Conditions [D]. Hefei:Hefei University of Technology, 2012.(in Chinese)
CHUNG T,YI K. Design and Evaluation of Side Slip Angle-Based Vehicle Stability Control Scheme on a Virtual Test Track [J]. Control Systems Technology,2006,14(2):224-234.
余卓平,高晓杰,张立军.用于车辆稳定性控制的直接横摆力矩及车轮变滑移率联合控制研究[J].汽车工程,2006,28(9):844-848.
Yu Zhuoping,Gao Xiaojie,Zhang Lijun. A Study on Coordination of Direct Yaw Moment Control and Variable Wheel Slip Control for Vehicle Stability [J]. Automotive Engineering,2006,28(9):844-848.(in Chinese)
NAGAI M, HIRANO Y,YAMANAKA S. Integrated Robust Control of Active Rear Wheel Steering and Direct Yaw Moment Control [J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 1997,27(5-6):416-421.
郭孔辉.汽车操纵动力学 [M]. 长春:吉林科学技术出版社,1991.
Guo Konghui. Vehicle Handling Dynamics [M]. Changchun:Jilin Science and Technology Press,1991.(in Chinese)
魏道高,王子涵,张翼天,等. 转向系间隙对操纵稳定性影响研究 [J].汽车工程,2014, 36(2): 139-144.
Wei Daogao,Wang Zihan,Zhang Yitian. A Study on the Influence of the Clearance in Steering System on Vehicle Handling and Stability [J]. Automotive Engineering,2014,36(2):139-144.(in Chinese)
唐锡宽,金德闻. 机械动力学 [M]. 北京:高等教育出版社,1983.
Tang Xikuan,Jin Dewen. Machine Dynamics [M]. Beijing:Higher Education Press,1983.(in Chinese)
靳春梅.含间隙机构非线性动态特性、控制及实验研究[D].西安:西安交通大学,2001.
Jin Chunmei. Nonlinear Dynamic Behaviors and Control and Experimental Researches on the Mechanism with Clea-rance Connections[D]. Xi'an:Xi'an Jiaotong University,2001.(in Chinese)
PACEJKA H B. Tyre and Vehicle Dynamics(2nd Edtion)[M]. USA:SAE,2006.
刘延柱,陈立群. 非线性振动 [M]. 北京:高等教育出版社,2001.
Liu Yanzhu,Chen Liqun.Nonlinear Vibration [M]. Beijing:Higher Education Press,2001.(in Chinese)
KREUZER E. 非线性动力学系统的数值研究 [M].凌复华,译. 上海:上海交通大学出版社, 1989.
KREUZER E. Numerical Investigation of Nonlinear Dy-namic System [M]. Ling Fuhua,Translate. Shanghai: Shanghai Jiaotong University Press,1989.(in Chinese)
