基于扫描测量的部分场分解方法及试验研究
2015-08-19古惠南郭明建穆国宝席忠民
古惠南+郭明建+穆国宝+席忠民

摘 要:采用扫描测量方式得到的非相干声场需分解成完全相干的部分场后才能用于近场声全息重建。目前虚相干法和偏相干法是部分场分解的主要方法,但是虚相干法误差较大,而且在应用中易受到声源特性等因素的影响而变得不稳定;偏相干法虽然能稳定地分解出部分场复声压幅值信息,但不能得到部分场的相位信息。为得到完整而稳定的全息面部分场复声压,通过改进偏相干法,得到一种新的部分场分解法——条件信号法。该方法将条件参考信号作为对应声源的部分场信号,通过频率响应函数变换得到具有稳定完整的幅值信息和相位信息的部分场。通过数值仿真和试验研究对虚相干法、偏相干法和条件信号法的分解效果进行比较,结果验证了偏相干法和条件信号法在分解部分场幅值时的有效性和条件信号法在分解部分场相位时的优越性。
关键词:非相干声场;部分场分解;条件参考信号;近场声全息
中图分类号:TB533文献标文献标识码:A文献标DOI:10.3969/j.issn.2095-1469.2015.03.03
近场声全息(Nearfield Acoustic Holography,NAH)技术是一种非常有效的噪声源识别、定位和声场可视化技术[1-2]。经过多年发展,该技术在空间变换算法和测量方法方面都取得了很多成果,先后提出了快照法、单参考传递函数法、多参考互谱测量法和声强测量法等多种全息面数据测量方法。
由于NAH技术要求在全息面上测量到的声场必须是完全相干的[3],但工程实际应用中的目标声场大部分是由若干个不相干或部分相干的声源所辐射声场叠加而成,此时单参考传递函数法和声强测量法就不再适用。而快照法和多参考互谱测量法仍然可以用于这种不相干或部分相干声场的NAH测量。但是快照法需要大量的传声器和并行测量通道,标定校准工作量比较大,设备成本高昂,不利于在工程实际应用中推广。所以,针对不相干或部分相干声场最合适的NAH测量方法是多参考互谱测量法。该方法只需要用小阵列(如线阵列)在全息面上按照一定的顺序采集声场,所需传声器少,设备成本低。
多参考互谱测量法首先需将测量到的非相干声场分解成若干个完全相干的部分场,再分别对这些部分场NAH重建,最后将重建后的声场进行叠加,得到需要的重建结果。针对部分场的分解,Hald最早提出了虚相干法,该方法借助奇异值分解(Singular Value Decomposition,SVD)将非相干声场分解成为若干完全相干的部分场[4-6]。但是,虚相干法分解得到的部分场和实际的部分场不是一一对应的,而且虚相干法在应用中很不稳定,会受到声源复声压幅值相位信息、参考传声器位置、测量时的环境噪声等因素的影响,导致分解得到的部分场的幅值和相位误差较大。之后,Tomlinson将偏相干理论引入部分场的分解[7],该方法能稳定地分解出部分场复声压幅值信息。由于该方法采用偏相干函数和条件谱计算部分场,而条件谱中没有相位信息,所以该方法不能得到部分场的相位信息。
为得到完整而稳定的全息面部分场复声压,本文对偏相干法进行改进,得到一种新的部分场分解方法——条件信号法。该方法首先求出部分场声源的条件参考信号,然后通过频率响应函数求出该部分场声源在场点中产生的部分场信号。该方法分解出的部分场有完整的幅值和相位信息,和实际的部分场更加接近,有利于NAH重建。
1 理论原理
对于两输入/单输出的简单系统,x1(t)和x2(t)为输入信号,则x2(t)可分解成两个独立的部分
。
式中,表示和输入1线性相关的部分信号;表示去掉输入1后输入2产生的条件信号。对式(1)作Fourier变换后可得:
。
式中,L12表示x1(t)和x2(t)之间的频率响应函数。
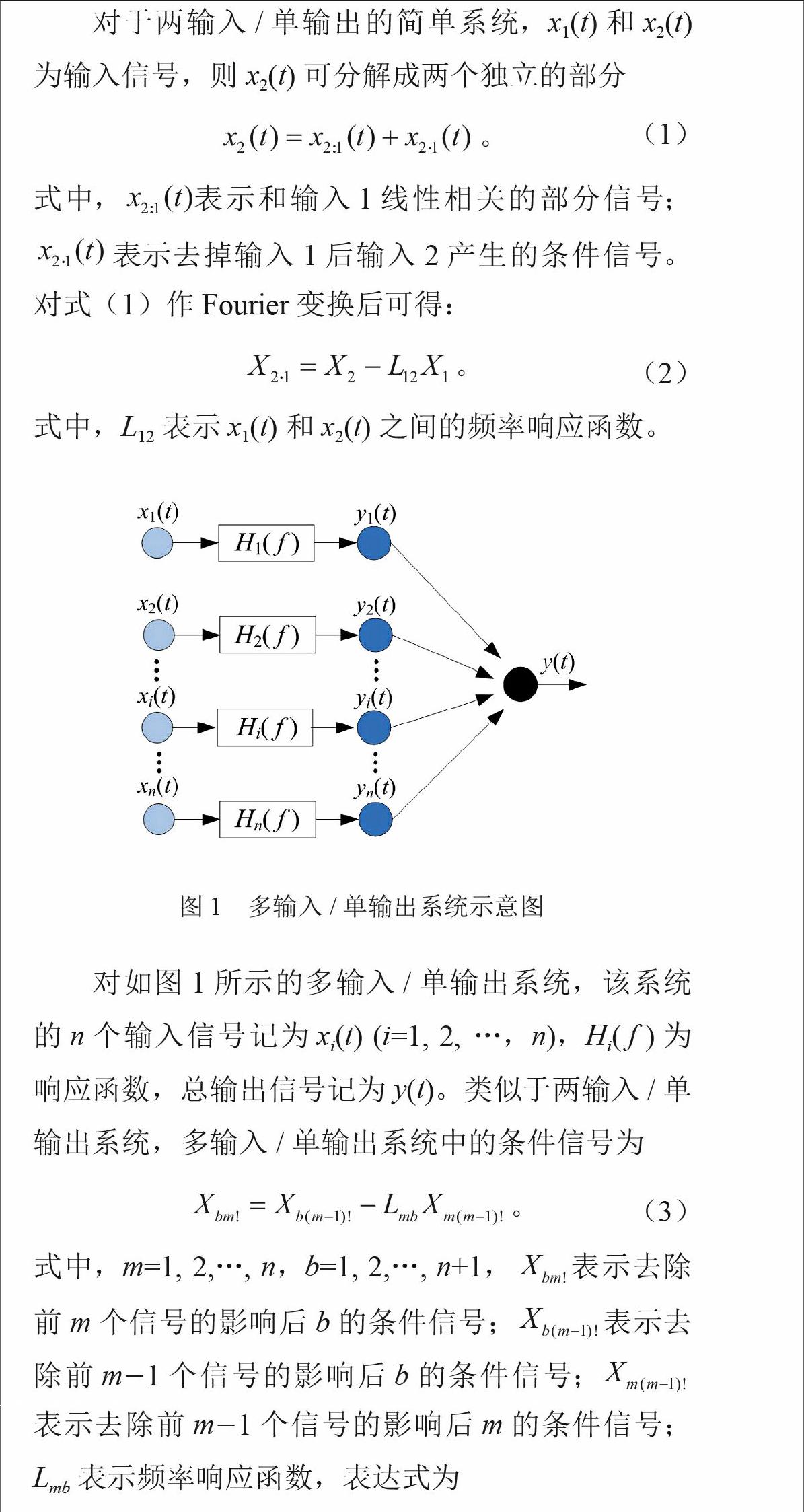
对如图1所示的多输入/单输出系统,该系统的n个输入信号记为xi(t) (i=1, 2, …,n),Hi(f)为响应函数,总输出信号记为y(t)。类似于两输入/单输出系统,多输入/单输出系统中的条件信号为
。
式中,m=1, 2,…, n,b=1, 2,…, n+1,表示去除前m个信号的影响后b的条件信号;表示去除前m-1个信号的影响后b的条件信号;表示去除前m-1个信号的影响后m的条件信号;Lmb表示频率响应函数,表达式为
。
式中,表示去除前m-1个信号的影响后信号m和b的条件互谱,表示去除前m-1个信号的影响后信号m的条件自谱。条件谱的计算公式为
。
式中,b=1, 2,…, n+1;表示去除前m个信号的影响后信号a和b的条件互谱;表示去除前m-1个信号的影响后信号a和b的条件互谱;表示去除前m-1个信号的影响后信号a和m的条件互谱。
本文提出的部分场分解过程如图2所示,假设共有R个声源,在每个声源附近布置一个参考传声器,即参考信号数n=R。然后,将测量到的n个参考信号作为输入信号,全息面上测量到的m个场点信号作为输出信号,比照图1所示的多输入/单输出系统计算条件信号和频率响应函数。
利用式(3)和式(4)迭代求出除去其它声源影响后的条件参考信号rn(n-1)!。通过式(4)和式(5)迭代求出条件参考信号rn(n-1)!和条件场点信号pj(n-1)!之间的频率响应函数Lnj。由于部分场n的声源在场点j处产生的部分场信号pnj和条件参考信号rn(n-1)!可以看成是完全相干的,因此将其它n-1个声源影响去除后的部分场信号可以通过频率响应函数Lnj变换获得,即
。
根据式(6)依次历遍所有场点j,可求出部分场n的复声压。然后依次将每个参考信号作为第n个参考信号,重复上述步骤,可求出其余部分场。
2 数值仿真
如图3所示,在声源面(z=0)上布置两个非相干的脉动球声源,声源的半径为0.05 m。声介质的密度为1.21 kg/m3,声速为340 m/s。全息面的位置zh=0.15 m,在全息面上划分21×21个场点。参考面位置为zr=0.05 m。仿真中脉动球的振动频率为200 Hz,400 Hz,600 Hz,800 Hz,1 000 Hz,1 200 Hz。分别用虚相干法、偏相干法和条件信号法分解全息面声压,并定义各部分场的复声压幅值的相对误差为
。
式中,为理论值;e为计算值;表示取2范数。
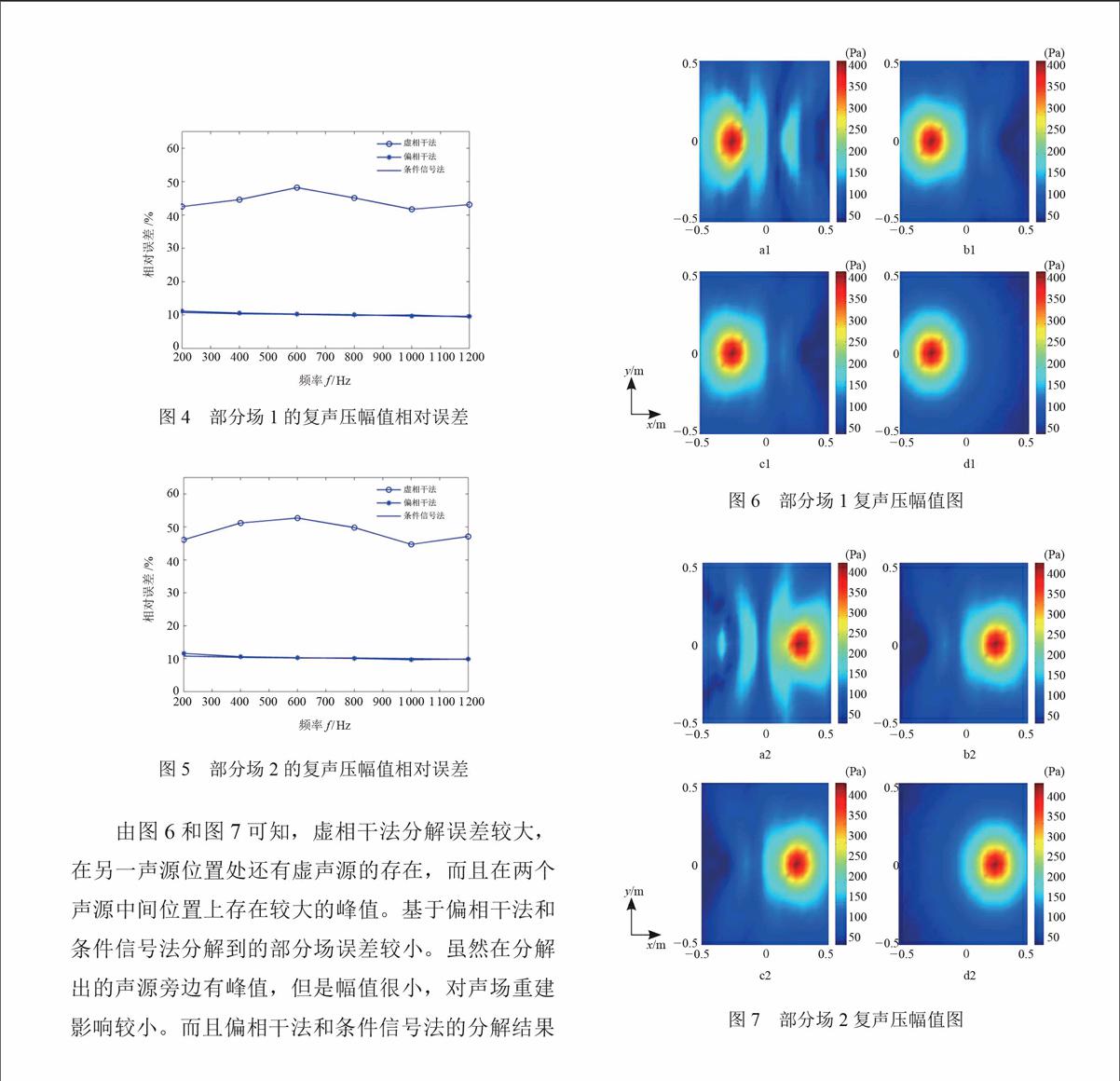
按照式(7)计算的相对误差结果如图4~5所示。由图4和图5中可知,通过偏相干法和条件信号法分解出的部分场复声压幅值的相对误差较小,保持在10%左右,其波动很小。用虚相干法分解出的部分场复声压幅值,由于受到声源复声压相位差、参考传声器位置等因素的影响,其相对误差较大,而且波动较大。由此可知,偏相干法和条件信号法比虚相干法稳健,分解出的复声压幅值和理论值更接近。为了进一步证实偏相干法和条件信号法在分解幅值时的稳定性以及条件信号法在分解相位信息时的优越性,给出了频率为1 000 Hz时的部分场分解结果,如图6~9所示。图6和图7分别为部分场1和2的复声压幅值图。图6中,a1为虚相干法结果,峰值为406.0 Pa;b1为偏相干法结果,峰值为430.3 Pa;c1为条件信号法结果,峰值为427.0 Pa;d1为理论声场结果,峰值为426.1 Pa。图7中,a2为虚相干法结果,峰值为441.8 Pa;b2为偏相干法结果,峰值为439.8 Pa;c2为条件信号法结果,峰值为434.4 Pa;d2为理论声场结果,峰值为435.1 Pa。图8和图9分别为部分场1和2的复声压相位图。图8中,a1为虚相干法结果;b1为偏相干法结果;c1为条件信号法结果;d1为理论声场结果。图9中,a2为虚相干法结果;b2为偏相干法结果;c2为条件信号法结果;d2为理论声场结果。
由图6和图7可知,虚相干法分解误差较大,在另一声源位置处还有虚声源的存在,而且在两个声源中间位置上存在较大的峰值。基于偏相干法和条件信号法分解到的部分场误差较小。虽然在分解出的声源旁边有峰值,但是幅值很小,对声场重建影响较小。而且偏相干法和条件信号法的分解结果无论是在形状上还是在幅值上都和理论部分场相吻合。由图8和图9可知,虚相干法能分解出部分场相位信息,但分解结果误差较大,在两声源位置中间的很多相位在分解过程中丢失,而且部分场2对应的相位很明显跟理论部分场相位相反,严重失真;偏相干法在分解过程中相位信息完全丢失,根本不能得到相位信息;条件信号法分解出的部分场相位整体上和理论部分场相位较一致。仿真结果证实了偏相干法和条件信号法在分解部分场幅值时的有效性和条件信号法在分解部分场相位时的优越性。
3 试验验证
试验是在半消声室内完成,实验室本底噪声小于16 dB。试验装置如图10所示,所用设备为两个音频特性不一样的音响,两个音响的纸盆中心位置分别为(-0.25 m,0,0)和(+0.25 m,0,0),通过两个独立的声源驱动,频率为1 000 Hz,两声源的相位差随机变化;多通道的信号采集器与调理器以及12个传声器组成的阵列等。全息测量面位于zh=0.15 m处,全息测量面的大小为1 m×1 m。全息面上划分21×21个场点,用扫描测量的方式测量声场信息。参考传声器布置在与声源面平行且距离为0.05 m的参考面上。分别用虚相干法、偏相干法、条件信号法分解部分场,结果如图11~14所示。图11和图12分别为部分场1和2的复声压幅值图。图11中,a1为虚相干法结果,峰值为414.1 Pa;b1为偏相干法结果,峰值为427.5 Pa;c1为条件信号法结果,峰值为420.5 Pa;d1为理论声场1结果,峰值为419.1 Pa。图12中,a2为虚相干法结果,峰值为417.0 Pa;b2为偏相干法结果,峰值为444.1 Pa;c2为条件信号法结果,峰值为437.6 Pa;d2为理论声场2结果,峰值为438.7 Pa。图13和图14分别为部分场1和2的复声压相位图。图13中,a1为虚相干法结果;b1为偏相干法结果;c1为条件信号法结果;d1为理论声场1结果。图14中,a2为虚相干法结果;b2为偏相干法结果;c2为条件信号法结果;d2为理论声场2结果。
由图11和12可知,虚相干法分解得到的部分场在另一个声源位置上有明显的虚声源,且两声源中间位置上有较大的峰值。由于在试验过程中不可避免地受到环境噪声的影响,试验得到的部分场误差更大。这说明虚相干法在工程实际应用中容易受到环境噪声的影响,很不稳定。而偏相干法和条件信号法在受到环境噪声影响的情况下仍然能够稳定分解出部分场幅值,而且分解结果和理论部分场幅值相比较,都极为接近。这证实了偏相干法和条件信号法在分解部分场幅值时的稳定性。由图13和图14可知,虚相干法分解得到的部分场在分解过程中丢失了很多相位信息,而且部分场2对应的相位很明显跟理论部分场相位相反,严重失真;偏相干法在分解过程中相位信息完全丢失,根本不能得到相位信息;条件信号法分解得到的部分场相位信息的试验结果和理论部分场的相位相吻合。试验结果证实了偏相干法和条件信号法在分解部分场幅值时的有效性和条件信号法在分解部分场相位时的优越性。
4 结论
为得到完整而稳定的全息面部分场复声压,本文对偏相干法进行改进,首先求出部分场声源的条件参考信号,然后通过频率响应函数求出该部分场声源在场点中产生的部分场信号。该方法分解得到的部分场具有完整而稳定的幅值信息和相位信息。通过数值仿真和试验研究对虚相干法、偏相干法和条件信号法的分解效果进行比较,结果表明:虚相干法不仅分解出的部分场误差较大,而且很不稳定,容易受到环境噪声、声源复声压幅值相位信息和参考传声器位置等因素的影响;偏相干法在分解部分场幅值方面很稳定,效果良好,但是不能得到相位信息;条件信号法在分解部分场幅值和相位时都很稳定,受到环境噪声等外界因素的影响较小,适合用于分解完全相干的部分场,有利于NAH重建。
参考文献(References):
WILLIAMS E G,MAYNARD J D,SKUDRZYK E J. Sound source Reconstructions Using a Microphone Array [J]. Journal of the Acoustical Society of America,1980, 68(1):340-344.
MAYNARD J D,WILLIAMS E G,LEE Y. Near-Field Acoustic Holography:I. Theory of Generalized Holography and Development of NAH [J]. Journal of the Acoustical Society of America,1985,78(4):1395-1413.
WILLIAMS E G. Fourier Acoustics:Sound Radiation and Nearfield Acoustical Holography [M]. London,UK:Academic Press,1999.
HALD J. STSF—a Unique Technique for Scan-Based Near-Field Acoustic Holography Without Restrictions on Coherence [J]. B&K Technical Review,1989(1):1-50.
MOOHYUNG L,BOLTON J S. Scan-Based Near-Field Acoustical Holography and Partial Field Decomposition in the Presence of Noise and Source Level Variation [J]. Journal of the Acoustical Society of America,2006, 119(1):382-393.
MOOHYUNG L,BOLTON J S,MONGEAU L. Application of Cylindrical Near-Field Acoustical Holo-graphy to the Visualization of Aeroacoustic Sources [J]. Journal of the Acoustical Society of America,2003, 114(2):842-858.
Tomlinson M A. Partial Source Discrimination in Near Field Acoustic Holography [J]. Applied Acoustics, 1999(57):243-261.
BENDAT J S,PIERSOL A G. Random Data:Analysis and Measurement Procedures(3rd edition)[M]. New York:Wiley,2000.
