基于混沌理论的自适应参数图像加密算法

李婵媛

摘 要：针对数字图像加密特点，提出一种基于混沌理论的自适应参数图像加密算法，将明文图像安全哈希算法（SHA-1）摘要协同用户密钥进行计算，将计算所得的参数作为自适应参数，输入混沌系统产生混沌序列对图像进行置乱和像素扩散，从而使不同的加密图像和加密参数对应不同的加密过程。实验结果表明，该算法密钥敏感度高，能够抵抗选择明文等攻击，具有较好加密性能。

关键词：图像加密 混沌 置乱 扩散 安全哈希算法

中图分类号：TP391 文献标识码：A 文章编号：1672-3791（2016）06（c）-0131-03

混沌非线性系统具有对初始条件的敏感性、序列的高度随机性等特征，能够很好适应密码系统的要求，因此，常用于图像加密算法[1-3]。该类算法利用混沌序列对图像像素点进行置乱和像素值的扩散操作，具有较好的图像加密效果。在图像加密过程中，由于混沌系统初始参数固定，生成的混沌序列和图像加密流程都是一致的，所以只要有足够的样本数据，就可以破解加密图像，从而算法存在安全性隐患。为增强加密算法的安全性，抵抗选择明文攻击，利用外部密钥与明文信息相结合控制混沌映射参数的思想[4-6]，该文提出一种自适应参数图像加密算法，图像加密过程中混沌初始参数依据明文图像而改变。

1 理论概述

高维混沌系统具有比低维混沌系统更复杂的动力学行为，该文采用三维Chen混沌系统进行加密[7]，具体方程如式（1），其中，为系统参数，当参数时，该系统处于混沌状态。

在图像加密过程中，如果密钥的产生不依靠明文图像，这样容易被己知明文和选择明文攻击。因此，该文在图像加密过程中混沌系统初始值的产生方式依赖于明文图像，不同图像对应的自适应参数均不同。该文在图像安全哈希算法（SHA-1）摘要基础上进行映射，并选映射后的数值作为自适应参数。

明文信息通过安全哈希算法（SHA-1），转换后产生以十六进制表示的哈希字符串，记为：，采用式（2）迭代计算出，其中表示向下取整，取任意正整数。式（1）混沌系统初始参数取值

2 自适应加密算法

该文加密过程共分为两个阶段：像素位置置乱和像素值扩散阶段。

2.1 像素位置置乱

步骤1：根据明文图像生成的哈希字符串根据式（2）生成混沌系统初始参数值，通过式（1）的混沌系统生成三组混沌序列。由于混沌序列的无周期性和无重复值，所以混沌序列的每个值在有序序列中均有唯一的位置标号。对混沌序列分别进行排序，生成三个位置序列分别记为，这些位置序列记录有序序列中各元素在原序列中的位置。

步骤2：利用位置索引置乱方法对大小为M×N的图像PM×N进行行和列置乱处理。设为图像矩阵第行或第列，对按照对应位置关系重新排序，得到序列。根据式（3）确定相对应的置乱序列，按照从上至下顺序进行行置乱，从左到右的顺序进行列置乱，得到置乱图像。式（3）中，mod求模取余，sum求和，Pi为图像矩阵第行或者第列。

该文算法置乱序列的选择需根据明文图像来确定，因此，图像置乱过程不仅与混沌序列的初始值相关，而且与明文图像有很大的相关性，此算法增加了置乱序列选择的随机性，增强了算法的安全性。

2.2 像素值扩散

通过像素位置置乱并没有改变图像各点的像素值，从而图像直方图不会改变，置乱后的图像仅破坏了原图像相邻像素之间的相关性。因此，需要进一步对置乱后图像的像素值进行扩散，以使密文图像抵御差分攻击。像素值的扩散采用按水平方向从左上角到右下角进行扫描每一个像素点，具体步骤如下。

步骤1：根据置乱图像生成的哈希字符串根据式（2）生成混沌系统初始参数值，通过式（1）混沌系统生成三组混沌序列，为增加像素值扩散的复杂性，将混沌序列按照组成长度为M×N的混沌序列D，在进行像素值扩散操作时，使用式（4）对序列D进行处理。式（4）中abs表示取绝对值，表示向下取整。

步骤2：通过式（5）对置乱图像进行像素值扩散操作，得到密文图像。其中为按位异或操作；为一个固定的灰度值。

综上步骤可得到密文图像。图像的解密过程是其加密过程的逆过程，此处不再做过多的详解。

3 实验及结果分析

为了验证该文加密算法的有效性，采用Matlab环境编程实现算法测试。用标准大小为512×512的Lena灰度图像作为明文图像，混沌系统初始参数己在算法步骤中给出，原始图像及密文图像如图1的（a）和（c）所示。从图1的（d）所示密文图像直方图可以看出，密文图像直方图呈均匀分布，提高了密文图像抵抗统计攻击的能力。接下来分析图像相邻像素对的平面分布及密钥敏感性等。

3.1 相邻像素相关性

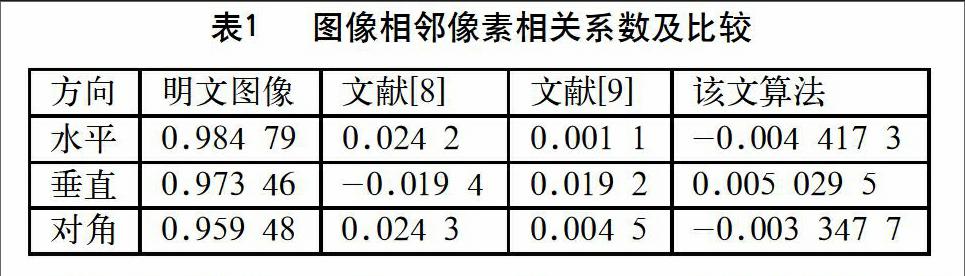
为进一步验证加密效果，检验明文图像和密文图像相邻像素的相关性，分别从明文图像和密文图像中随机选取2 000对水平、垂直和对角三个方向上相邻像素对，计算其相关系数[5]。表1列出了明文图像与密文图像在三个方向上相邻像素的相关系数，并给出了文献[8，9]算法与该文算法对图像加密后的相关系数比较。从表1可知，明文图像在三个方向上相关性均较强，相邻像素点分布集中，相关系数均接近1；而密文图像在三个方向上的相邻像素相关性均较弱，相邻像素值都均匀地分布在了整个像素空间，相关系数均趋近于0，表明明文图像的统计特征已被随机的扩散到密文图像中。

此外，从表1可知，该文算法加密后，其密文图像的相关性统计性能达到了文献[8，9]所示算法的加密性能，并在一定程度上优于文献[8]和文献[9]所示算法的加密性能。

3.2 加密图像的信息熵

灰度图像信息熵的计算公式，其中：为灰度值的出现概率。对于加密图像而言，其理想图像信息熵为8。该文算法得到Lena密文图像的信息熵为7.999 3，信息熵趋近于8，说明具有较好的加密效果。

3.3 密钥敏感度分析

加密算法应要求密钥具有足够的敏感性，即使密钥有微小变化，也无法正确解密图像。在此算法中，使用三维混沌序列，有初始参数以及自适应参数，图2是对分别对密钥进行微小修改，保持其他参数不变，进行解密的实验结果。因为当一个密钥发生微小变化时，都无法对密文图像正确进行解密，而且没有显示任何明文信息，所以该文算法对密钥极度敏感。

4 结语

该文给出了基于混沌系统地适应参数图像加密算法，所提出的图像加密算法将原图像SHA-1值和三维混沌系统初始参数联合作为密钥，自适应参数依据图像哈希字符串计算获取，所以不同图像的加密过程中产生的混沌序列不相同，图像置乱和扩散过程中与明文图像有很大的相关性。实验结果表明，密文图像直方图呈均匀分布，相邻像素相关性低，信息熵接近理论值8，密钥和明文图像敏感性均较强，在抵御统计攻击，差分攻击等能达到很好效果，具有较好的加密性能。

参考文献

[1] Li C Q，Li S J，Chen O R，et al.Cryptanalysis of an image encryption scheme based on a compound chaotic sequence[J].Image and Vision Computing，2009，27（8）：1035-1039.

[2] 张晓强，工蒙蒙，朱贵良.图像加密算法研究新进展[J].计算机工程与科学，2012，34（5）：1-6.

[3] Li C Q，Zhang L Y，Ou R，et al.Breaking a novel colour image encryption algorithm based on chaos[J].Nonlinear Dynamics，2012，70（4）：2383-2388.

[4] 寇丽娟，祝英俊，蒋联源，等.基于信息分存的整数小波大容量数据隐藏方法[J].光电子·激光，2009（9）：1203-1207.

[5] 赵锋，吴成茂.自编码和超混沌映射相结合的图像加密算法[J]. 计算机辅助设计与图形学报，2016，28（1）：119-128.

[6] 卫娟，戴冬.基于双重异或操作运算的图像加密机制[J].计算机应用与软件，2015，6（32）：300-302.

[7] 吕金虎，陆君安，陈士华.混沌时间序列分析及其应用[M].武汉：武汉人学出版社，2002.

[8] Teng L，Wang X.A bit-level image encryption algorithm based on spationtemporal chaotic system and self-adaptive[J].Optics Communications，2012，285（20）：4048-4054.

[9] Wang X，Luan D.A novel image encryption algorithm using chaos and reversible cellular automata[J].Communications in Nonlinear Science and Numerical Simulation，2013，18（11）：3075-3085.