被动天棚阻尼悬架降阶与优化
2015-08-19蒋涛陈龙张孝良
蒋涛+陈龙+张孝良


摘 要:采用基于Routh稳定判据的Pade逼近法对被动天棚阻尼悬架系统进行降阶,寻找阶次低、元件少的ISD悬架结构。建立四分之一悬架模型,运用统一目标函数的遗传算法优化结构的参数,对比分析了传统被动、被动天棚阻尼和降阶ISD三种悬架系统的性能。结果表明,与被动天棚阻尼悬架相比,降阶ISD悬架的车身加速度、轮胎动载荷和悬架动行程均方根值都不同程度逼近被动天棚阻尼悬架,能够实现被动天棚阻尼悬架的主要性能,说明经降阶优化的ISD悬架综合性能可以接近被动天棚阻尼悬架,研究结果从理论上验证了基于Routh稳定判据的Pade逼近法的有效性。
关键词:Routh稳定判据;Pade逼近法;天棚阻尼;ISD悬架;参数优化
中图分类号:U463.33文献标文献标识码:A文献标DOI:10.3969/j.issn.2095-1469.2015.03.05
基于经典隔振理论的传统悬架由弹簧和阻尼器构成,一些学者通过优化被动悬架的结构参数来提高悬架的隔振性能,其性能潜力已达极限,进一步提高其减振性能受限。惯容器的出现以及“惯容器-弹簧-阻尼”悬架体系的确立突破了传统被动悬架的性能瓶颈,进一步拓展了经典隔振理论,开辟出一条改善悬架性能的新途径[1-3]。
理想天棚阻尼作为一种控制策略,在可控悬架的控制研究中得到了广泛应用[4-6]。由于理想天棚阻尼要求阻尼元件必须与惯性系相连,传统被动车辆悬架系统无法满足该条件。文献[7]提出一种理想天棚阻尼的被动实现方法,设计出一种不需要能量输入,不依赖控制系统的被动天棚阻尼悬架。
被动天棚阻尼悬架系统是一种速度反馈系统,利用“惯容-弹簧-质量”系统的反共振现象,抑制车身共振并转换为惯容器的共振,使天棚阻尼吸收惯容器的振动能量,从而以被动的形式实现理想天棚阻尼的效果,达到抑制车身共振,改善行驶平顺性的目的[7]。然而被动天棚阻尼悬架是两级串联的结构,由5个元件组成,结构复杂,阶次较高,工程化条件较差。
本文基于Routh稳定判据的Pade逼近法对被动天棚阻尼悬架系统进行降阶,寻找出符合或近似于此传递函数的机械系统,并采用统一目标函数的遗传算法优化结构参数,探索阶次低、元件少、性能能够达到或接近被动天棚阻尼悬架的ISD悬架结构。
1 基于Routh稳定判据的Pade逼近法降阶
1.1 降阶基础
惯容器如同机械系统中的弹簧和阻尼器一样,是一种真正的两端点元件,其动力学表达式为
。
根据机械阻抗的定义,可以导出惯容器、弹簧和阻尼三种元件的机械阻抗表达式:
。
。
。
式中,f为施加于元件两端点上等大反向的力,kN;v为端点速度,m/s;b为惯容系数,kg;k为弹簧刚度,kN/m;c为阻尼系数,kN·m·s-1;s为拉氏变换复变量。
由惯容器、弹簧和阻尼三种元件的机械阻抗及串、并联系统的阻抗特性可得到图1中a所示的被动天棚阻尼悬架的机械阻抗:
式中,
为了保持车身的高度,悬架结构一定有弹簧这一弹性元件,悬架系统可以视为图1中b所示的元件组合,因此被动天棚阻尼悬架的等效机械阻抗Y(s)可改写成:
。
式中,;;;;
;
;
。
降阶过程采用两步法:首先利用Routh近似法求取低阶简化模型的分母多项式,然后用Pade逼近法求分子多项式。这样,既能保证降阶后的稳定性,又能吸取Pade逼近法的优点[8]。
1.2 Routh近似法
设高阶系统的传递函数
。
式中,m≤n。运用Routh稳定判据于的分母多项式,将其改写成下式(设n为偶数):
。
设。
根据式(6),可以将被动天棚阻尼悬架模型的降阶归纳为对K(s)的降阶(其中n=2),运用Routh法可以将K(s)的分母Q(s)改写成:
因此
。
式中,。
1.3 Pade逼近法
设对应高阶系统的传递函数有一有理函数 :
。
则称为函数G(s)的( j,k)阶Pade逼近。 的分子多项式系数、分母多项式系数由线性方程组确定[9]。
通过式(12)可以求出d0,则
将K1(s)带入式(6)可得
式中,;
。
进一步化解可以得到
式中,;。
降阶后的机械阻抗对应的物理实现模型如图2所示。
2 降阶模型动力学建模及优化
2.1 悬架系统建模
应用复域机械阻抗法建立1/4悬架模型,如图3所示。
该1/4悬架模型拉普拉斯变换下的动力学方程为
。
式中,m1为簧下质量,kg;m2为簧上质量,kg;z0为路面随机输入;z1,z2分别为簧下、簧上质量垂直位移,m;z0,z1,z2分别为z0,z1,z2的拉氏变换形式;kt 为轮胎刚度,kN/m;Y(s)为复域悬架阻抗。
根据式(16)可以求出车身加速度对z0的传递函数:
。
轮胎动载荷Fd对z0的传递函数:
。
悬架动行程 fd对z0的传递函数:
。
式中,。
路面输入采用文献[9]给出的模型,可以得到时间频率表达的路面谱:
。
式中,G0为路面不平度系数;u为车辆行驶速度,m/s; f为时间频率,Hz;指数p表示双对数坐标下谱密度曲线的斜率。
令,则车身加速度、轮胎动载荷和悬架动行程的功率谱密度分别为[10]
。
。
。
相应的均方根值分别为
。
。
。
2.2 多目标悬架参数优化
为了使降阶ISD悬架结构性能逼近被动天棚阻尼悬架最佳性能,对该结构元件参数进行优化。车身加速度均方根值BA、轮胎动载荷均方根值DTL和悬架动行程均方根值SWS是悬架性能重要的评价指标,因此这是一个多目标优化的问题。线性加权法可以有效权衡各目标函数,采用该方法将各目标函数统一为一个目标函数。将降阶ISD悬架结构性能与被动天棚阻尼悬架进行对比,侧重于乘坐舒适性,选取加权因子w1=0.54,w2=0.33,w3=0.13,故优化的统一目标函数为
。
式中,BAsky、DTLsky、SWSsky表示被动天棚阻尼悬架的最优均方根值,、、表示降阶ISD悬架均方根值。
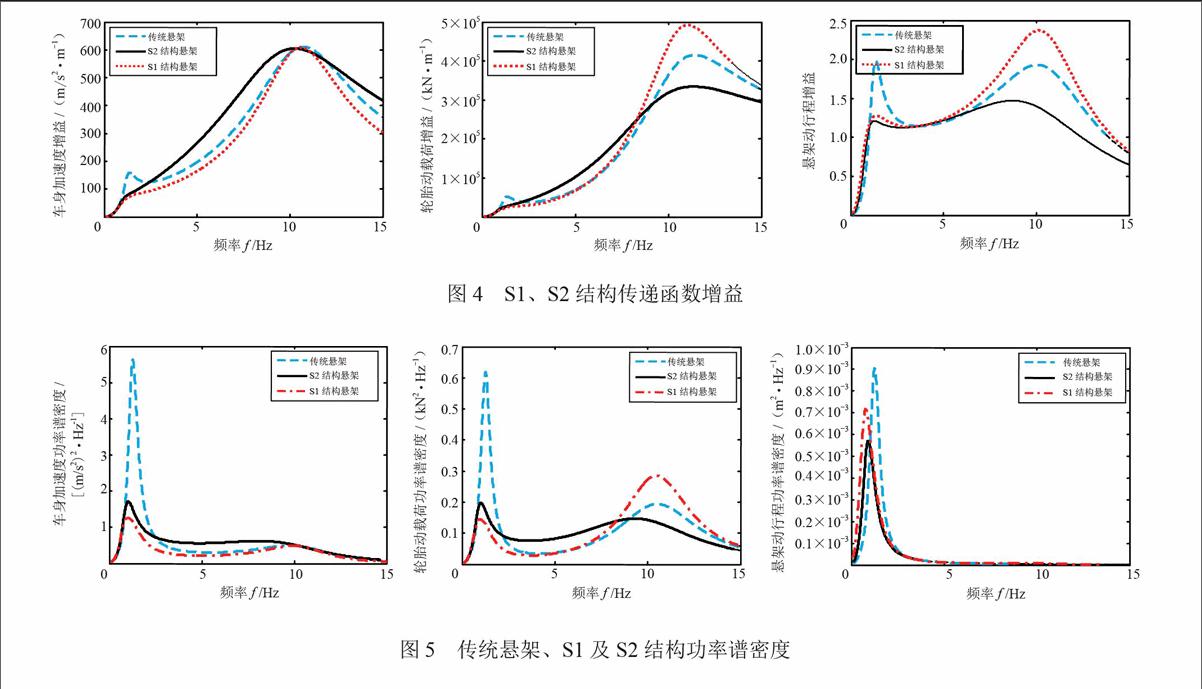
某款成熟轿车悬架及被动天棚阻尼悬架相关参数见表1,遗传算法最大的遗传代数为50,代沟为0.9。运用多目标遗传算法来实现统一目标函数f(x)的迭代过程,取弹簧刚度k为可调整参数,搜索每个k值对应点的最佳性能指标,找出相对应的c、b值。被动天棚阻尼悬架S1及降阶ISD悬架S2传递函数增益如图4所示,与被动天棚阻尼悬架S1相比,降阶ISD悬架S2的车身加速度、轮胎动载荷增益同样能够抑制1~3 Hz低频段共振峰及9~12 Hz的高频段共振峰,中频段性能也较接近,悬架动行程增益在全频域内性能优于被动天棚阻尼悬架S1。总体上,降阶ISD悬架S2的车身加速度、轮胎动载荷和悬架动行程都不同程度逼近被动天棚阻尼悬架S1,优化参数见表1。
3 系统性能分析
设在某典型路面上,车速为20 m/s,取不平度系数G0为5×10-6 m3/cycle,指数P为2.5,采用数值积分法将各自悬架系统的机械阻抗及系统参数代入式(17)~(26),响应均方根值见表2,车身加速度、轮胎动载荷和悬架动行程的功率谱密度如图5所示。
由表2可知,与传统被动悬架相比,降阶ISD悬架S2与被动天棚阻尼悬架S1的车身加速度均方根值分别减少了5.9%和23.8%,轮胎动载荷均方根值分别减少了6.1%和0.3%,悬架动行程均方根值分别减少了3.4%和增加了2.0%。根据式(27)可知,当min f(x) =1时,该降阶ISD悬架性能与被动天棚阻尼悬架接近,结果得到f(x) =1.101 0,说明降阶ISD悬架S2取代被动天棚阻尼悬架S1时,车辆综合性能较接近。
由图5可知,降阶ISD悬架S2在低频段功率谱密度曲线与被动天棚阻尼悬架S1基本重合,中频段功率谱密度较S1略大,高频段功率谱密度较S1有所减小。因此,与被动天棚阻尼悬架相比,降阶ISD悬架车身加速度功率谱密度在1~3 Hz及9~15 Hz 内的改善程度与被动天棚阻尼悬架非常接近,悬架动行程整体性能优于被动天棚阻尼悬架,保证了车辆的乘坐舒适性,降阶ISD悬架轮胎动载荷在1~3 Hz接近被动天棚阻尼悬架,在9~15 Hz优于被动天棚阻尼悬架,保证了车辆的行驶安全性,说明降阶ISD悬架综合性能在全频域范围都较接近被动天棚阻尼悬架。
4 结论
(1)与被动天棚阻尼悬架相比,降阶ISD悬架的车身加速度、轮胎动载荷和悬架动行程均方根值都不同程度逼近被动天棚阻尼悬架,能够实现被动天棚阻尼悬架的主要性能。
(2)降阶ISD悬架由三元件组成,阶次低、元件少,研究结果从理论上验证了基于Routh稳定判据的Pade逼近法的有效性,说明经降阶优化的ISD悬架综合性能可以接近被动天棚阻尼悬架。
参考文献(References):
SMITH M C,WANG F C. Performance Benefits in Passive Vehicle Suspensions Employing Inerters [J]. Vehicle System Dynamics,2004,42(4):235-257.
CHEN M Z Q, PAPAGEORGIOU C,SCHEIBE F, et al. The Missing Mechanical Circuit Element [J]. Circuits and Systems Magazine,IEEE,2009,9(1):10-26.
WANG F C,CHAN H A. Mechatronic Suspension Design and Its Applications to Vehicle Suspension Control [C]//Decision and Control,CDC 2008,47th IEEE Conference on IEEE,2008:3769-3774.
RAKHEJA S,SANKAR S. Vibration and Shock Isolation Performance of a Semi-Active on-off Damper [J]. Journal of Vibration,Acoustics Stress and Reliability in Design, 1985,107(4):398-403.
DO A L,SENAME O,DUGARD L,et al. An Extension of Mixed Sky-Hook and ADD to Magneto-Rheological Dampers [C]// 4th IFAC Symposium on System,Struc-ture and Control,Ancona,Italy,2010.
LIU Y,WATERS T P,BRENNAN M J. A Comparison of Semi-Active Damping Control Strategies for Vibration Isolation of Harmonic Disturbances [J]. Journal of Sound and Vibration,2005(280):21-39.
张孝良,聂佳梅,汪若尘,等. 基于惯容-弹簧-阻尼结构体系的被动天棚阻尼悬架系统[J]. 农业机械学报, 2013,44(10):10-14.
Zhang Xiaoliang,Nie Jiamei,Wang Ruochen,et al. Passive Skyhook Suspension System,Based on Inerter-Spring-Damper Structural System [J]. Transactions of the Chinese Society for Agriculture Machinery,2013,44(10):10 -14.(in Chinese)
李祖枢. 高阶线性定常系统的低阶逼近新方法——具有可调参数的模型简化 [J]. 重庆大学学报 (自然科学版),1980(4):69-90.
Li Zushu. A Novel Low Order Approximation Method of Higher Order Linear Time Invariant Dynamic Systems:Model Reduction with Adjustable Parameters [J]. Chong- qing University(Natural Science),1980(4):69 -90.(in Chinese)
喻凡,林逸.汽车动力学 [M]. 北京: 机械工业出版社, 2005.
Yu Fan,Lin Yi. Vehicle Dynamics [M]. Beijing:China Machine Press,2005.(in Chinese)
陈龙,张孝良,江浩斌,等. 基于机电系统相似性理论的蓄能悬架系统 [J]. 中国机械工程,2009,20(10):1248-1250.
Chen Long,Zhang Xiaoliang,Jiang Haobin,et al. Vehicle Suspension System Employing Inerter Based on Electrical-Mechanical Analogies Theory [J]. China Mechanical Engineering,2009,20(10):1248-1250.(in Chinese)
