辐射开环空间绳系机器人编队自旋转速最优控制
2015-08-17黄攀峰刘彬彬
黄攀峰,张 帆,刘彬彬,马 骏
(1.西北工业大学航天学院智能机器人研究中心,陕西西安710072;2.西北工业大学航天飞行动力学技术重点实验室,陕西西安710072)
辐射开环空间绳系机器人编队自旋转速最优控制
黄攀峰1,2,张 帆1,2,刘彬彬1,2,马 骏1,2
(1.西北工业大学航天学院智能机器人研究中心,陕西西安710072;2.西北工业大学航天飞行动力学技术重点实验室,陕西西安710072)
辐射开环空间绳系机器人(tethered space robot,TSR)编队是一种新型的空间绳系编队系统,其在构型稳定性、任务灵活性以及燃料消耗方面具有明显的优势。研究了辐射开环TSR编队自旋转速最优控制问题。首先建立了辐射开环TSR编队的自旋动力学模型;然后对编队自旋转速控制问题以及hp-自适应伪谱法求解最优控制问题的基本原理进行了描述,并设计了基于hp-自适应伪谱法的编队自旋转速闭环最优控制系统;最后通过仿真算例对设计的闭环最优控制系统进行验证和分析。
空间绳系机器人编队;辐射开环;自旋转速;最优控制
0 引 言
空间绳系机器人(tethered space robot,TSR)是一种新型的具有绳系结构的空间机器人系统[1-8],其主要应用于空间在轨捕获和轨道清理任务。辐射开环TSR编队系统是一种新型的采用辐射开环编队构型的TSR编队系统,由一个空间平台、多个TSR及多根绳系组成。空间平台具备多绳系回收、释放及控制能力,以辐射开环形式通过绳系与TSR连接,空间平台能够通过自身的执行机构产生自旋运动,进而促使整个编队构型以一定的角速度在空间中进行自旋运动,利用自旋运动产生的离心力维持各TSR绳系的张力并保持编队构型。特殊的编队形式和自旋运动使得辐射开环TSR编队系统具有以下优点:
(1)绳系结构和自旋运动使得编队构型获得较高的稳定性,并能减少维持编队构型所需的燃料消耗;
(2)通过控制各TSR绳系的收放进而能够改变编队系统构型,提高空间任务灵活性;
(3)相比各TSR首尾相互连接的闭环形式的编队构型,辐射开环形式的编队构型中,整个编队系统的自旋运动以及TSR绳系的收放和控制均可以由处于编队中心的空间平台实现,控制方式简单。
基于以上优点,辐射开环TSR编队系统在多种空间任务中具有潜在应用价值,包括空间多点观测,太阳帆、大型空间天线、大型太阳能电池板等空间轻质膜、网结构的柔性支撑,具有轻质量、低成本的特点。
自旋运动能够促进编队构型的稳定,也是辐射开环TSR编队在大多数空间任务中的主要运动状态。不仅在空间观测等需要连续改变编队中各TSR相对位置的空间任务中具有重要意义,而且在太阳帆支撑、构建空间柔性平台等空间任务中也能够依靠自旋运动产生的离心力达到稳定柔性结构的目的,即达到利用自旋运动产生的离心力保持编队构型的目的。另外,特殊的辐射开环构型使得整个编队的展开、保持、重构以及自旋运动的控制等都可以由空间平台单独完成。可见自旋运动对辐射开环TSR编队具有极其重要的意义。自旋转速是用来衡量编队自旋运动快慢的主要物理量。从实际应用方面来说,不同的空间任务中所要求的编队自旋转速不同,而且同一空间任务中也有可能要求自旋转速根据需要发生变化。因此,编队自旋转速控制是辐射开环TSR编队的关键技术之一。
辐射开环TSR编队的自旋转速最优控制问题可以描述为:在某种条件约束下(编队构型约束、控制量约束等),依靠空间平台的自旋扭矩控制编队的自旋转速沿着一定的轨迹,从初始状态转移到要求的最终状态,并满足某种指标最优(燃料消耗最少或转移时间最短)。本文针对辐射开环TSR编队的自旋转速最优控制问题展开研究。首先在合理假设条件下建立了辐射开环TSR编队的自旋动力学模型;然后对编队自旋转速控制问题以及hp-自适应伪谱法求解最优控制问题的基本原理进行了描述,并设计了基于hp-自适应伪谱法的编队自旋转速闭环最优控制器;最后通过仿真算例对提出的最优控制器进行了验证和分析。
1 编队自旋动力学
1.1 建模假设
图1为辐射开环TSR编队构型和典型空间应用示意图。其自旋动力学模型与一般绳系卫星模型的主要差别在于:前者的绳系长度在100m量级,而后者大多在10km甚至100km量级;另外,前者在二维平面内进行自旋运动,面外运动可忽略,各TSR的绳系始终保持直线张紧状态,系绳拉力作为离心力来保持编队构型,而后者并不自旋,绳系拉力可作为控制量(仅能提供拉力)。因此,绳系的质量和柔性特性的影响相对于绳系卫星模型来说便可以忽略。另外,由于绳系较短,决定了整个编队的孔径较小,因此在空间环境下重力梯度、轨道摄动等外部因素的影响较小,可忽略。
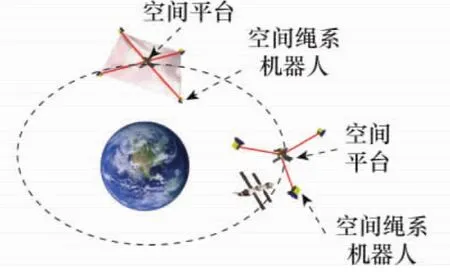
图1 辐射开环TSR编队
文献[9-15]中关于空间柔性网展开的研究为辐射开环TSR编队的动力学建模提供了一种新的思路,即从自旋运动的特性出发建立辐射开环TSR编队的自旋动力学模型。理想的辐射开环TSR编队系统中各TSR相对空间平台对称分布,因此编队系统自旋运动时各TSR的运动也完全相同,因此本文以结构最为简单的二体辐射开环TSR编队系统为基础,推导并建立辐射开环TSR编队系统自旋运动的动力学模型。建模过程中将空间平台看作具有一定转动半径的刚体轮毂,各TSR看作质点,空间平台通过执行机构能够提供一定的自旋扭矩,并能够很好地控制各TSR的绳系拉力;另外,忽略形变、摩擦和环境因素引起的能量耗散。
1.2 参考系与坐标定义
图2为二体辐射开环TSR编队系统简化结构示意图,编队系统中包括空间平台和与空间平台依靠绳系连接的两个TSR(TSR1和TSR2)。图中O1为空间平台的几何中心,O2为TSR1的绳系与空间平台的连接点,分别以O1和O2为原点建立参考坐标系O1x1y1和O2x2y2,其中O2x2沿TSR1绳系方向,O2y2垂直于O2x2。为了描述方便,将连接TSR1和TSR2的两条绳系称为旋臂1和旋臂2。设旋臂1和旋臂2的长度大小分别为L1和L2,设旋臂1和旋臂2承受的绳系拉力大小分别为T1和T2,TSR1和TSR2质量分别为m1和m2,空间平台的转动半径和转动惯量分别为r0和I,空间平台提供的自旋扭矩为M。
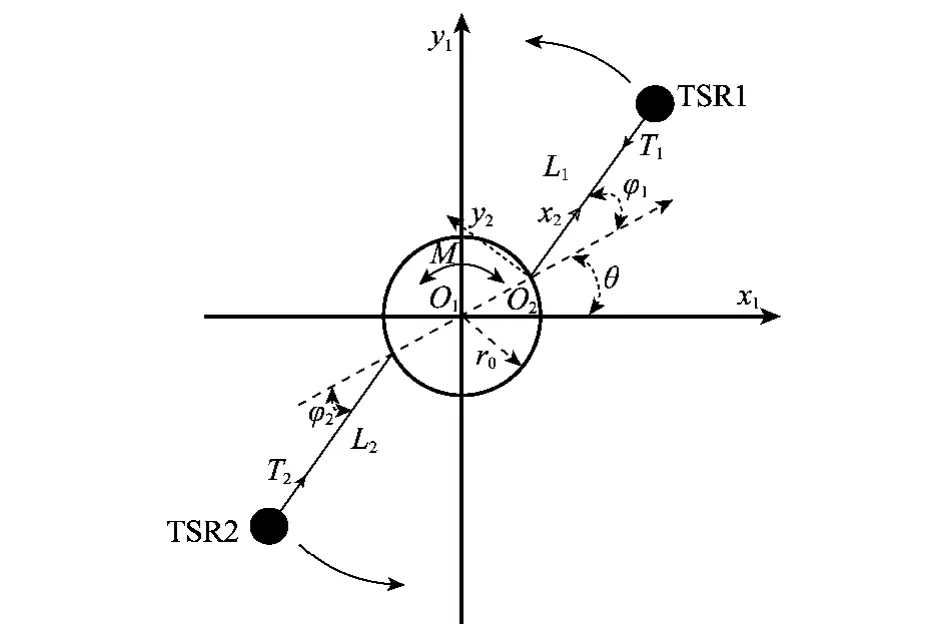
图2 二体辐射开环TSR编队简化模型
1.3 自旋动力学模型
设参考坐标系O1x1y1和O2x2y2中的单位坐标列阵分别为
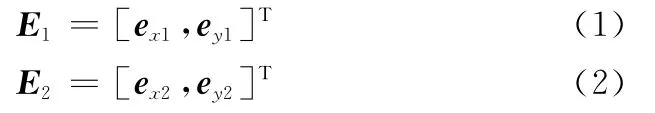
式中,ex1、ey1、ex2和ey2分别为坐标系O1x1y1和O2x2y2中的单位坐标向量。辐射开环TSR编队系统自旋过程中,空间平台在旋转的同时受到TSR1和TSR2的绳系拉力作用。由于假设条件中将空间平台看作刚体轮毂,因此坐标系O1x1y1中,由刚体定轴转动角动量定理可得

式中,θ、φ1和φ2的定义如图2所示(下文中将角度偏差φ1和φ2称为旋臂角);ω为空间平台的自旋角速度。显然各TSR受到的外力只有空间平台连接的绳系的拉力,对于TSR1有
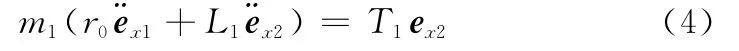
由泊松公式可以得到
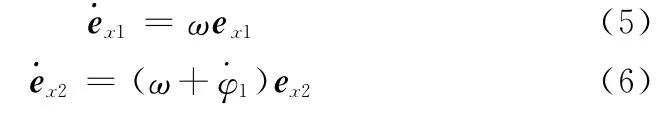
将式(5)和式(6)代入式(4),并将ex1、ey1投影在O2x2y2坐标系中,整理可得
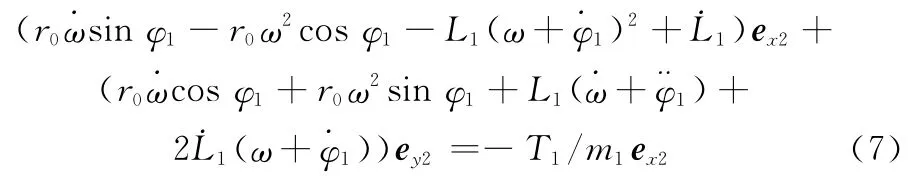
进而可以得到
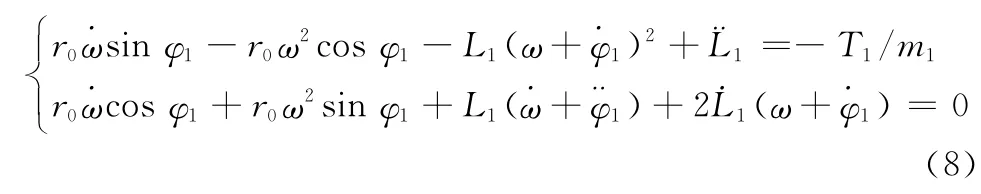
同理,对于TSR2有

综合式(3)、式(8)和式(9)可得
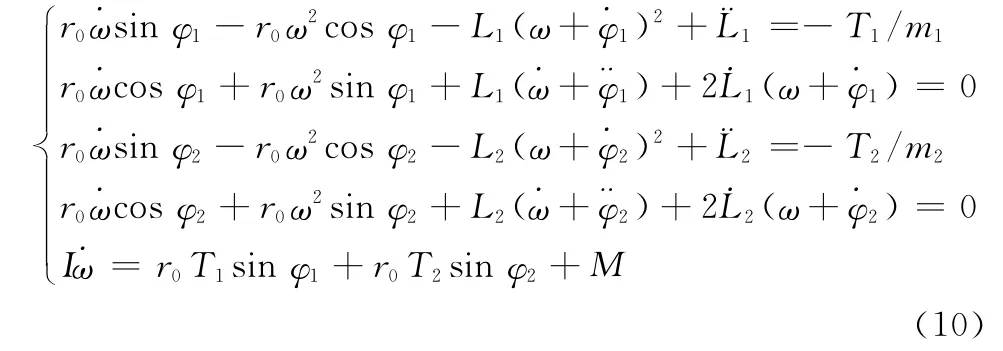
式(10)即为二体辐射开环TSR编队系统自旋运动时的动力学模型,进一步可扩展到n体辐射开环TSR编队系统的情况

式中,Ln为连接TSRn的旋臂n的长度;Tn为旋臂n承受的绳系拉力;mn为TSRn的质量;φn为旋臂n的旋臂角。式(11)即为n体辐射开环TSR编队的自旋动力学模型,是具有2n+1个非线性微分方程的方程组。
本文将对辐射开环TSR编队自旋转速最优控制问题展开研究。首先在式(11)的基础上提出以下假设条件:
(1)编队自旋转速控制过程中各旋臂的长度不变且相等,即
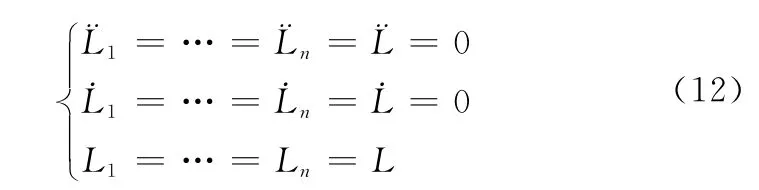
(2)各TSR具有相同的质量,即

在以上假设条件下,辐射开环TSR编队自旋转速控制过程中,各旋臂承受的绳系拉力变化将完全相同,各旋臂的变化也将完全相同。此时式(11)可以写为
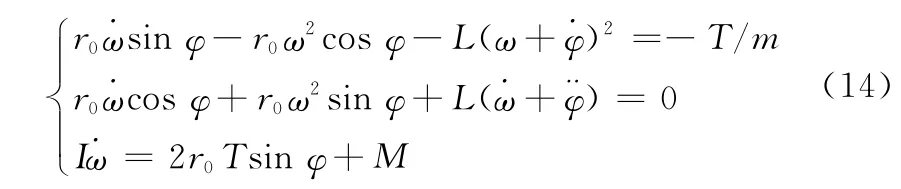
式中,T为编队中旋臂承受的绳系拉力;φ为编队中的旋臂角;L为编队中旋臂的长度。
2 编队自旋转速最优控制
2.1 编队自旋转速最优控制问题
自旋运动是辐射开环TSR编队大多数空间任务中的主要运动状态。自旋转速是衡量编队自旋运动快慢的主要物理量。实际应用中,不同的空间任务中所要求的编队自旋转速不同,而且同一空间任务中也有可能要求自旋转速根据需要发生变化。从第1节内容可以看到,辐射开环TSR编队的自旋动力学模型是由多个非线性微分方程组成的复杂的方程组,其分析和计算都非常复杂,从而对编队自旋转速控制的研究造成了一定的难度。
一般情况下,希望辐射开环TSR编队的自旋转速发生变化后,编队仍然能够保持理想的辐射开环构型并以变化后的自旋转速作匀速自旋运动。理想的辐射开环构型要求旋臂角φ及其角速度˙φ保持为零值,同时自旋转速ω保持恒定值。因此将φ、˙φ和ω作为编队自旋转速控制任务中需要控制的状态变量。另外,从式(14)可以看到,辐射开环TSR编队自旋转速控制过程中,可能的控制量包括空间平台的自旋扭矩M和各旋臂的绳系拉力T。但是考虑到旋臂的绳系拉力需要提供编队自旋运动过程所需要的离心力,其大小将根据编队自旋转速的变化而变化。在这种情况下,旋臂绳系拉力能够提供的控制量大小必然非常有限,其实现也非常困难。另一方面,空间任务有可能要求编队自旋转速发生较大范围、快速的变化,因此需要较大的控制量来实现编队自旋转速的控制。综合以上考虑,本文将采用实现较为简单,且能提供较大控制量的空间平台的自旋扭矩M作为编队自旋转速控制过程的控制量。
最优控制是现代控制理论的一个重要组成部分。其所研究的问题是:对一个控制系统,在给定的性能指标要求下,如何选择控制规律,使性能指标达到最优(极值)。将辐射开环TSR编队自旋转速控制问题用最优控制理论进行求解,即寻找最优控制变量u*(t),在一系列约束条件下,使得编队自旋转速控制过程中控制量(空间平台的自旋扭矩M)的消耗达到最少,或者所用的时间最少,写成目标函数的形式,即为
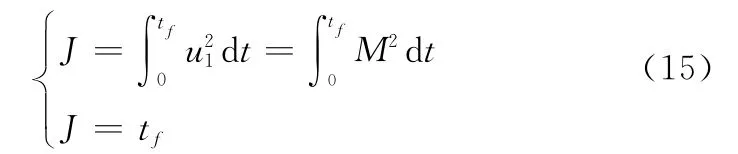
在约束条件方面,主要包括动力学约束、路径约束以及终端约束。取状态变量为

取控制量为

则由式(14)可以得到
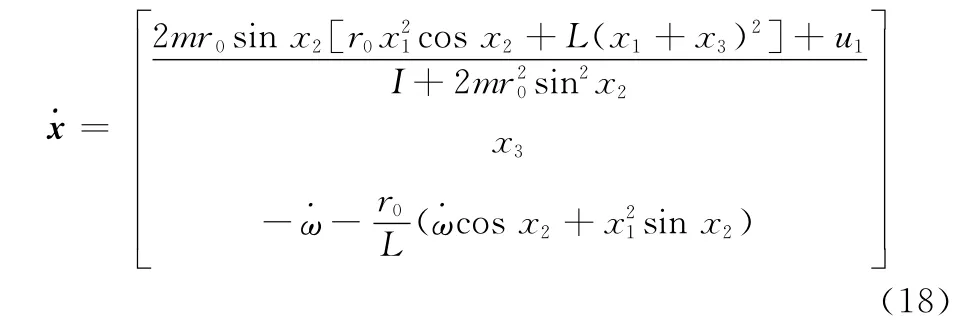
式(18)即为编队自旋转速控制过程的动力学约束。状态变量ω、φ和,控制量M也需要满足一定的条件,即路径约束

另外,编队系统自旋转速的初始状态和最终状态也需要满足一定的终端约束
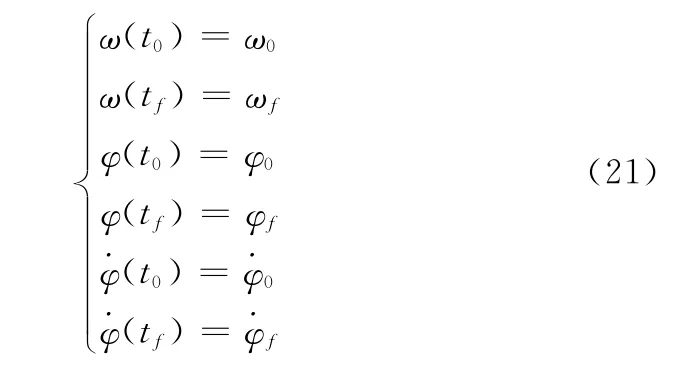
2.2 hp-自适应伪谱法基本原理
hp-自适应伪谱算法为经典的Guass伪谱算法和有限元法的结合,相对传统的Guass伪谱算法,它在求解复杂的非光滑问题时,精度更高且收敛速度更快。本文采用hp-自适应伪谱算法求解辐射开环TSR编队自旋转速控制过程的最优解。
针对式(15)、式(18)~式(21)构成的最优控制问题,hp-自适应伪谱算法首先将时域区间分为若干段,并在每段上选取一定数量的Legendre-Gauss点作为配点,然后在每个单元上利用Lagrange多项式逼近系统的状态变量和控制变量,并通过插值函数的微分和被积函数的高斯积分来近似系统的状态微分和性能指标,从而将连续的最优控制问题转化为离散的非线性规划问题,最后通过使用自适应的配点调整策略和相关的规划求解算法求解离散后的非线性规划问题,从而实现对于最优控制问题的求解。由以上的分析可知,hp-自适应伪谱算法主要包括两个部分。
2.2.1 Legendre-Gauss-Radau离散
通过K+1个节点(0=t0<t1<…<tk=T)将最优控制问题在t∈[0,T]上分为K个单元,对于任意单元k,通过以下变换将时间区间由t∈[tk-1,tk]转换到τ∈[-1,+1]:
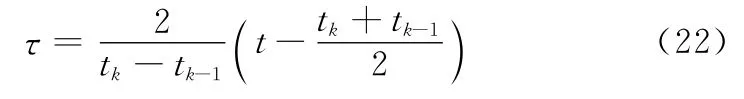
将系统的性能指标转换为
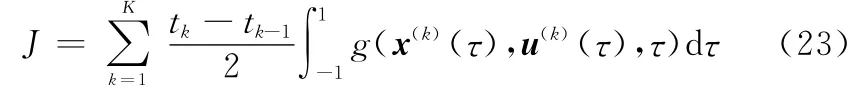
将系统的动力学约束转换为
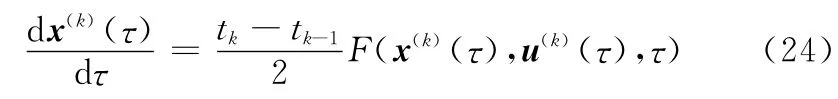
同理可以实现对路径约束条件和边界约束条件的转换。这样的分段方式还引入了内点约束

在任意单元k上选取Nk个LG点,并使用分段的起始点τ=-1和所选取的LG点构造Nk+1阶的Lagrange插值多项式,则有
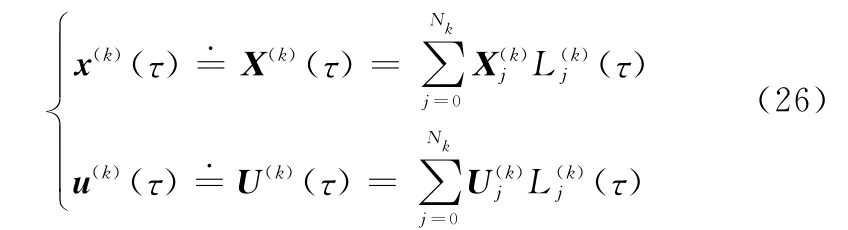
其中
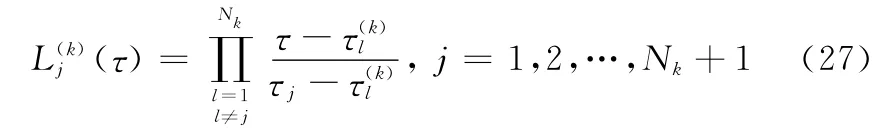
系统性能指标可进一步离散化为

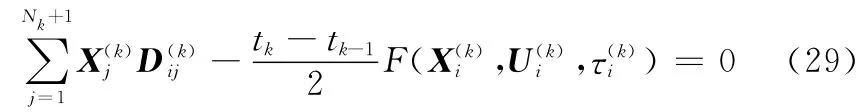
式中,i=1,2,…,Nk,矩阵D满足

式中,i=1,2,…,Nk;j=1,2,…,Nk+1。任意单元k上的终端状态可以近似为
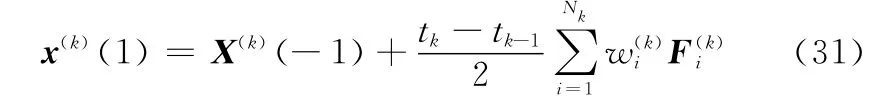
将式(26)和式(31)代入系统的路径约束、边界约束和内点约束,从而可以将系统的路径约束条件和终端约束条件离散化为

在完成对于指标函数和系统约束的经典Guass伪谱算法离散后,连续的最优控制问题就转化为了离散的非线性规划问题。
2.2.2 hp-自适应配点调整
对于任意的单元,选取相邻两个配点的中点,令
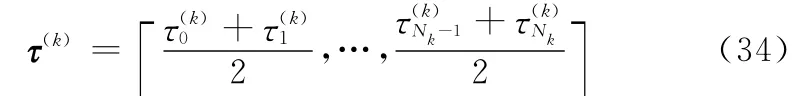
由式(26)计算系统的状态向量矩阵X(k)∈RNk×n以及控制向量矩阵U(k)∈RNk×m,定义重点残差矩阵^R1和^R2为
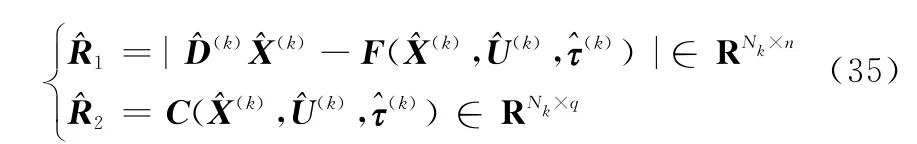
式中,m、n和q分别表示状态变量、控制变量和路径约束的维数。定义单元k上的残差e(k)为
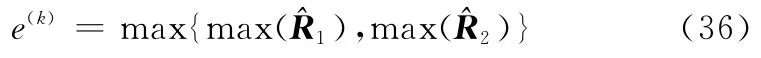
取矩阵^R1每一行的最大值组成列向量r(k),引入规范化残差向量

式中,r(k)为算数平均值,满足

按照以下步骤进行自适应配点调整:
步骤1 若e(k)小于设定的阈值,则不进行调整;
步骤2 若e(k)大于设定的阈值,且e(k)为矩阵^R2中的元素,则在不满足路径约束处重新分段;
步骤3 若e(k)大于设定的阈值,且e(k)为矩阵^R1中的元素,β(k)中的元素数量级相近,则通过增加单元内的配点数来减小误差;
步骤4 若e(k)大于设定的阈值,且e(k)为矩阵^R1中的元素,β(k)中的元素数量级相差较大,则在最大元素对应点处重新进行分段。
2.3 闭环最优控制器设计
利用hp-自适应伪谱算法可以得到辐射开环TSR编队自旋转速控制过程中的最优控制u*(t)和最优状态轨迹x*(t)。为了保证编队的自旋转速能够沿着规划的轨迹变化,本文设计了如图3所示的闭环最优控制系统。
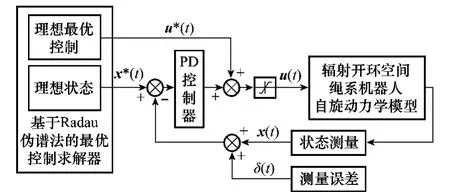
图3 闭环最优控制系统
首先通过基于hp-自适应伪谱法的求解器获得编队自旋转速的理想控制律u*(t)和理想状态变化x*(t),然后通过PD控制器对真实测量的状态变化x(t)与理想状态x*(t)之间的偏差进行控制,进而将PD控制器输出与理想控制律u*(t)的和作为闭环控制的输出u(t),最后通过u(t)对辐射开环TSR编队的自旋转速进行控制。其中δ(t)为测量误差。
3 仿真算例与分析
本节将通过数字仿真的形式,对提出的辐射开环TSR编队自旋转速闭环最优控制系统进行验证和分析。仿真场景设计如下:初始状态时二体辐射开环TSR编队以ω=π/12的角速度在空间中作匀速自旋运动,此时旋臂角和旋臂角速度均为0。空间任务要求编队自旋转速加速到ω=π/3,并以ω=π/3的自旋转速继续进行匀速自旋运动。编队自旋转速的加速过程中要求旋臂角满足一定的约束条件,当加速结束后,旋臂角及其加速度变为0。
仿真过程中PD控制器的参数根据实际的仿真效果进行调整。假设空间平台的自旋扭矩M为幅值有限的连续可控量。另外,仿真过程中利用Matlab环境的基于hp-自适应伪谱法的最优控制工具箱GPOPS,获得辐射开环TSR编队的理想控制u*(t)和理想状态x*(t)。实际应用中,状态测量都可能会产生误差,因此为了验证闭环控制回路控制策略的有效性,仿真中在闭环控制回路中增加了测量误差。设测量误差δ(t)为幅值在[-0.05,0.05]之间均匀分布的噪声。其他主要仿真参数如表1所示。

表1 仿真参数
3.1 仿真算例1
目标函数的选取以空间平台的自旋扭矩消耗最少为原则,即
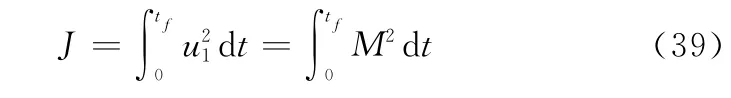
动力学约束采用式(18),路径约束取为
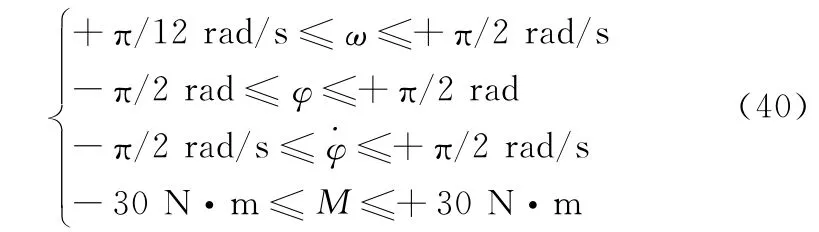
注意到旋臂角φ被限制在-π/2到+π/2之间,这是因为旋臂角φ超出这个角度限制时,由于二体辐射开环构型的几何特性,旋臂将与空间平台发生缠绕。为了避免缠绕现象,旋臂角的角速度限制在-π/2~+π/2之间。终端约束取为
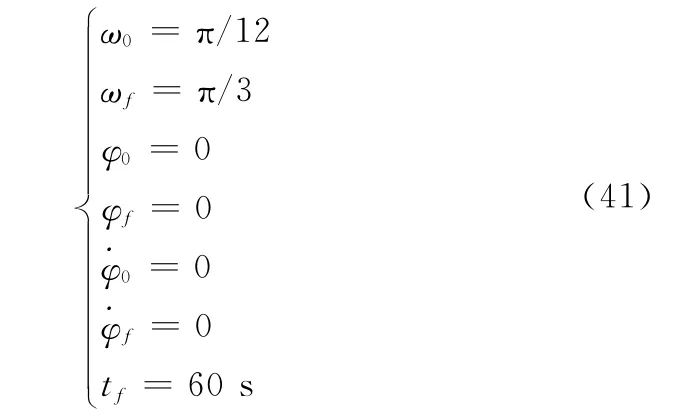
以上终端约束要求编队自旋转速的初始状态时和最终状态时,编队的自旋转速保持不变,旋臂角及其角速度也保持零值,即保证编队最终状态时编队构型和自旋运动的稳定性。
在以上目标函数和约束条件下,编队自旋转速闭环最优控制系统的仿真结果如图4~图7所示。
图4~图6分别为闭环最优控制策略作用下编队自旋转速ω、旋臂角φ和旋臂角角速度˙φ随时间的变化情况,同时图中还将各状态变量的理想值和实际值进行了比较。编队自旋转速ω、旋臂角φ和旋臂角角速度˙φ的理想值是基于hp-自适应伪谱算法的求解器得出的最优状态轨迹。
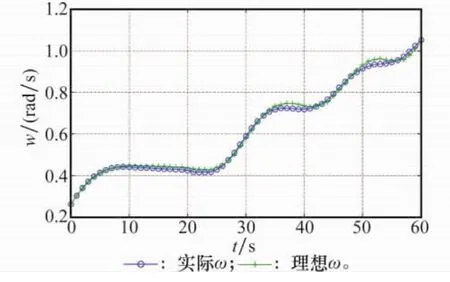
图4 ω随时间变化曲线(仿真算例1)

图5 φ随时间变化曲线(仿真算例1)
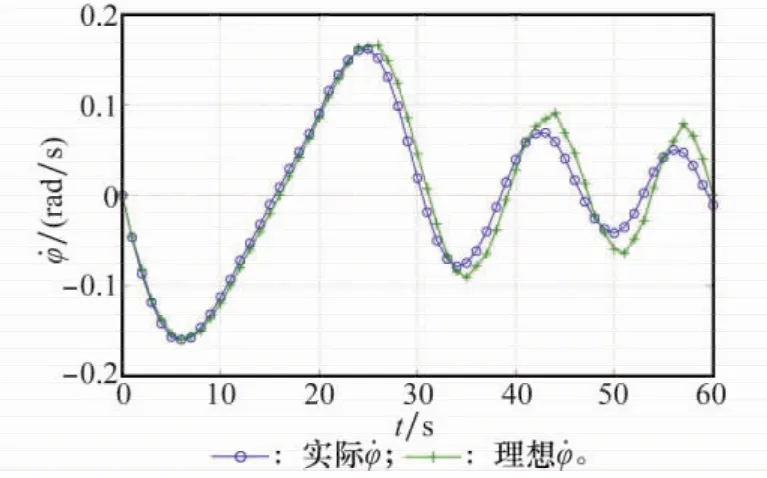
图6 ˙φ随时间变化曲线(仿真算例1)
从图中可以看到,在满足约束条件的前提下,编队自旋转速ω、旋臂角φ和旋臂角角速度˙φ的理想值能够有效地从初始状态转移到要求的终值状态,其实际值在闭环控制策略的作用下也能够很好地跟踪理想值的变化。
图7为控制量M的理想值和实际值随时间的变化曲线。从图中可以看到,hp-自适应伪谱法求解的理想控制量M是约束条件下较为平滑的曲线,而图中M的实际值为沿着理想值曲线作小幅度振荡的曲线,但M的实际值总体变化趋势与理想值相同。这是因为闭环控制回路中有按测量误差进行控制的PD控制器,实际控制量u(t)是hp-自适应伪谱法求解的理想的u*(t)与PD控制器输出的控制量之和。

图7 M随时间变化曲线(仿真算例1)
3.2 仿真算例2
目标函数以控制时间最短为原则,即

动力学模型采用式(18),路径约束同算例1中式(40),终端约束取为

在以上目标函数和约束条件下,编队自旋转速闭环最优控制系统的仿真结果如图8~图11所示。图8~图10分别为闭环最优控制策略作用下编队自旋转速ω、旋臂角φ和旋臂角角速度˙φ随时间的变化情况,图中将各状态变量的理想值和实际值进行了比较。与算例1相同,编队自旋转速ω、旋臂角φ和旋臂角角速度˙φ的理想值是基于hp-自适应伪谱算法的求解器得出的最优状态轨迹。采用控制时间最短为原则的目标函数时,基于hp-自适应伪谱算法求解出的最优控制u*(t)作用下的编队自旋转速ω、旋臂角φ和旋臂角角速度˙φ从初值状态转移到最终状态所消耗的最短控制时间为tf=53.50s。
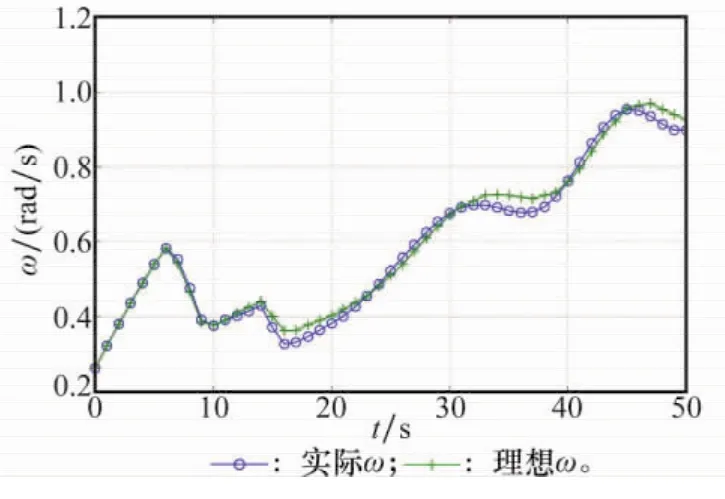
图8 ω随时间变化曲线(仿真算例2)
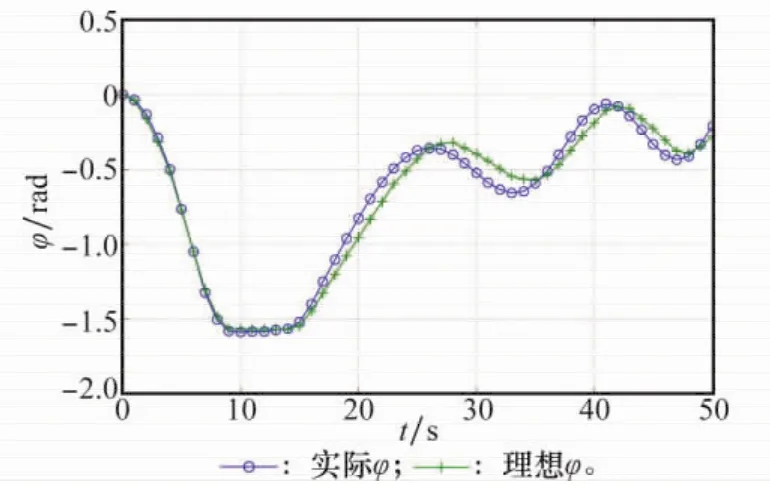
图9 φ随时间变化曲线(仿真算例2)

图10随时间变化曲线(仿真算例2)
另外,从图中可以看到,在满足约束条件的前提下,编队自旋转速ω、旋臂角φ和旋臂角角速度的理想值能够有效地从初始状态转移到要求的终值状态,其实际值在闭环控制策略的作用下也能够很好地跟踪理想值的变化。但是无论是理想值还是实际值,编队自旋转速ω、旋臂角φ和旋臂角角速度的变化曲线均不如算例1中以控制量消耗最少为原则的目标函数情况下的仿真曲线平稳。编队自旋转速ω的转移曲线振荡较为明显,旋臂角φ在转移过程中也一度接近了约束条件的边界。因此在式(42)中的目标函数情况下,能够获得最短的控制时间,但在相同的状态约束条件下,编队自旋转速的转移过程不及算例1中编队自旋转速的转移轨迹平稳。
图11为控制量M的理想值和实际值随时间的变化曲线。与算例1类似,理想控制量M是约束条件下较为平滑的曲线,而M的实际值为沿着理想值曲线作小幅度振荡的曲线,但M的实际值总体变化趋势与理想值相同。与算例1相比,由于目标函数要求以最短的时间实现编队的自旋转速转移过程,因此控制量M的消耗量更大。
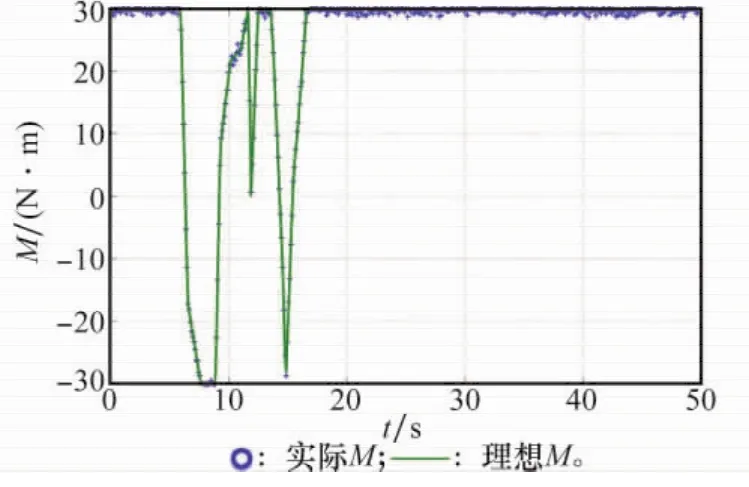
图11 M随时间变化曲线(仿真算例2)
4 结 论
编队自旋转速控制是辐射开环TSR编队的关键技术之一。本文研究了辐射开环TSR编队的自旋转速最优控制问题。建立了辐射开环TSR编队自旋动力学模型;提出了编队的自旋转速最优控制问题;设计了基于hp-自适应伪谱法的编队自旋转速闭环最优控制系统,并通过仿真算例进行了验证和分析。仿真结果表明,设计的闭环最优控制系统能够有效地应用在辐射开环TSR编队自旋转速控制任务中。
[1]Nohmi M,Nenchev D N,Uchiyama M.Momentum control of a tethered space robot through tether tension control[C]∥Proc.of the IEEE International Conference on Robotics &Automation,1998:920-925.
[2]Nohmi M.Attitude control of a tethered space robot by link motion under microgravity[C]∥Proc.of the IEEE International Conference on Control Applications,2004:424-429.
[3]Xu X D,Huang P F,Meng Z J,et al.Research on attitude fault tolerant control method for space tethered robot[J].Journal of Astronautics,2012,33(8):1096-1103.(徐秀栋,黄攀峰,孟中杰,等.空间绳系机器人姿态容错控制方法研究[J].宇航学报,2012,33(8):1096-1103.)
[4]Xu X D,Huang P F,Meng Z J.Space tethered robot coordinated control method for approaching the target.[J].Acta Aeronautica et Astronautica Sinica,2013,33(5):1222-1231.(徐秀栋,黄攀峰,孟中杰.空间绳系机器人逼近目标协调控制方法[J].航空学报,2013,33(5):1222-1231.)
[5]Wang D K,Huang P F,Meng Z J,et al.Coordinated attitude control of the combination system after capture by a tethered space robot.[J].Acta Aeronautica et Astronautica Sinica,2013,34(8):1998-2006.(王东科,黄攀峰,孟中杰,等.空间绳系机器人抓捕后复合体姿态协调控制研究[J].航空学报,2013,34(8):1998-2006.)
[6]Hu Q L,Zhang J,Ma G F.L2-gain based adaptive sliding mode coordinated attitude control of satellite formation with time-varying delays[J].Systems Engineering and Electronics,2013,35(11):2356-2363.(胡庆雷,张健,马广富.含时变时延的卫星编队姿态协同自适应滑模L2增益控制[J].系统工程与电子技术,2013,35(11):2356-2363.)
[7]Xu X D,Huang P F,Ma J.Coordinated position and attitude control method of tethered space robot[C]∥Proc.of the IEEE International Conference on Robotics and Biomimetics,2013:1526-1531.
[8]Meng Z J,Huang P F.Coordinated approach control method of tethered space robot system[C]∥Proc.of the IEEE Conference of Industrial Electronics and Applications,2013:1314-1318.
[9]Tibert G,Gardsback M.Space webs final report[R].Stockholm:European Space Agency,2006.
[10]Pizarro-Chong A,Misra A K.Dynamics of multi-tethered sat-ellite formations containing aparent body[J].Acta Astronautica,2008,63(11/12):1188-1202.
[11]Tibert G,Lennon A.Deployment strategies for the space tow solar sail[C]∥Proc.of the 1st International Symposium on Solar Sailing,2007:27-29.
[12]Gärdsback M,Tibert G.Deployment control of spinning space webs[J].Journal of Guidance,Control,and Dynamics,2009,32(1):40-50.
[13]Gärdsback M,Tibert G.Optimal deployment control of spinning space webs and membranes[J].Journal of Guidance,Control,and Dynamics,2009,32(5):1519-1530.
[14]Gärdsback M.Deployment control of spinning space webs and membranes[R].Stockholm:Royal Institute of Technology,Department of Mechanics,2008.
[15]Gärdsback M,Tibert G,Izzo D.Design considerations and deployment simulations of spinning space webs[C]∥Proc.of the 48th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,2007:1829-1838.
E-mail:pfhuang@nwpu.edu.cn
张 帆(1986-),女,博士研究生,主要研究方向为空间绳系机器人及其编队协同控制。
E-mail:978436992@qq.com
刘彬彬(1990-),男,硕士研究生,主要研究方向为空间绳系机器人编队动力学与控制。
E-mail:liubinflip@163.com
马 骏(1985-),男,博士研究生,主要研究方向为空间绳系系统动力学与控制。
E-mail:majun315415@163.com
Optimal control of the rotating velocity of hub-spoke tethered space robot formation
HUANG Pan-feng1,2,ZHANG Fan1,2,LIU Bin-bin1,2,MA Jun1,2
(1.Research Center of Intelligent Robotics,School of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China;2.National Key Laboratory of Aerospace Flight Dynamics,Northwestern Polytechnical University,Xi’an 710072,China)
The hub-spoke tethered space robot(TSR)formation is a novel formation system.The stability,flexibility and fuel consumption of the hub-spoke TSR formation system have been significantly improved.The optimal control problem of the rotating velocity of the hub-spoke TSR formation system is proposed and studied.Firstly,an analytical model is used to describe the rotating hub-spoke TSR formation system.Secondly,the optimal control problem of the rotating velocity and the theory of the hp-adaptive pseudospectral method are described.Thirdly,a closed-loop optimal control system based on the hp-adaptive pseudospectral method is established.Finally,some digital imitations are implemented to validate the proposed closed-loop optimal control system.
tethered space robot(TSR)formation;hub-spoke;rotating velocity;optimal control
V 445.4
A
10.3969/j.issn.1001-506X.2015.06.21
黄攀峰(1974-),男,教授,博士,主要研究方向为空间机器人动力学与控制、空间机器人遥操作技术。
1001-506X(2015)06-1362-08
2014-04-14;
2014-09-15;网络优先出版日期:2014-11-05。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20141105.1513.007.html
国家自然科学基金(11272256)资助课题
