基于雷达辐射源信号特征的类别信息辅助GM-PHD滤波器
2015-08-17朱友清周石琳
朱友清,周石琳
(国防科学技术大学电子科学与工程学院,湖南长沙410073)
基于雷达辐射源信号特征的类别信息辅助GM-PHD滤波器
朱友清,周石琳
(国防科学技术大学电子科学与工程学院,湖南长沙410073)
雷达辐射源目标跟踪在军事应用领域具有重要的意义。结合目标类别信息有助于提高高斯混合概率假设密度(Gaussian mixture-probability hypothesis density,GM-PHD)滤波器多目标跟踪的性能,但电子侦察系统获得的雷达辐射源信号信息无法直接应用于上述滤波器。为此,先利用辐射源信号特征进行雷达类型识别,然后基于可传递信度模型根据雷达-平台的配属关系将该识别结果转换到与已知类别信息相同的辨识框架内。在此基础上,采用相容系数度量其相似度用以近似GM-PHD滤波器中的量测似然值,从而实现类别信息的辅助目标跟踪。仿真实验表明,在不同的杂波密度下所提方法能够有效提高GM-PHD滤波器的跟踪性能。
多目标跟踪;高斯混合概率假设密度滤波器;雷达辐射源信号;可传递信度模型
0 引 言
电子侦察是一种被动接收敌方电磁信号的无源探测方式,相比有源探测,它具有侦察范围广、作用距离远、隐蔽性好、抗干扰性强等优点[1-2]。鉴于雷达在军事领域的突出地位,电子情报侦察系统在实际应用过程中的一个重要任务就是对搭载雷达辐射源的平台目标进行跟踪,为精确打击武器的使用提供情报支持。与传统的多目标跟踪算法不同,基于概率假设密度(probability hypothesis density, PHD)滤波器[3]的目标跟踪方法有效地避免了复杂的数据关联问题,被广泛应用于地面移动目标跟踪[4]、视频目标跟踪[5]、机动目标跟踪[6]、检测前跟踪[7]、多传感器目标跟踪[8-9]等诸多领域。而在线性高斯系统下,文献[10]提出了一种具有闭合解的PHD滤波器,简称为高斯混合概率假设密度(Gaussian mixture-probability hypothesis density,GM-PHD)滤波器。由于该滤波器具有计算量小、目标状态容易提取等优点,该方法在实际应用过程中得到了较多研究学者的关注。
另一方面,由于受到无源侦察系统自身特性的限制[2],电子侦察获得的目标位置信息仍然存在较大的误差,仅利用该位置信息进行目标的跟踪,其效果往往不理想。为此,不少学者提出了结合目标运动信息和辅助特征信息的改进目标跟踪算法[11-14]。其中类别信息是最常用的一种目标属性信息,Bar-Shalom等人利用一个混淆矩阵将目标类别信息结合到数据关联的过程中,提高了量测信息与目标的关联准确性,并对目标的类别概率进行了递归更新[12]。类似地,文献[13]将目标信号类别信息(target signal classification information,TSCI)引入到联合概率数据关联(joint probabilistic data association,JPDA)算法中以计算其可行性矩阵,从而改进邻近多目标的跟踪性能。此外,由于目标的跟踪与分类存在着一定的耦合关系,相互之间具有辅助作用,因此文献[14]将类别辅助信息引入到GM-PHD滤波器中,实现了多机动目标的联合检测、跟踪与分类。
虽然上述的这些方法都能有效地利用类别信息辅助提高目标跟踪的性能,但是针对雷达辐射源搭载平台的目标跟踪问题仍然存在着一些不足。一方面,电子侦察获得的辐射源信息一般为载频、重频、脉宽等信号参数信息,而不是直接可用的类别属性信息,需要通过一定的雷达辐射源识别算法对其进行分类。另一方面,雷达辐射源识别的分类结果为雷达的类型,而已知目标的类别信息一般是通过其他侦察手段(比如影像数据)获得的,其对应的类别信息一般为平台(比如驱逐舰)。因此这两种类别信息属于不同的辨识框架[15],不能直接进行比较,但它们又存在着一定的配属关系,需要进行信息的转换以实现相同类型信息的相似性度量。而本文正是针对这两个方面的问题开展研究,通过雷达辐射源识别和证据转换将类别信息应用到GM-PHD滤波器中,辅助进行辐射源目标跟踪以提高跟踪性能。
1 结合类别信息的GM-PHD滤波器
步骤1 预测
假设第k-1时刻GM-C-PHD滤波器的强度函数为
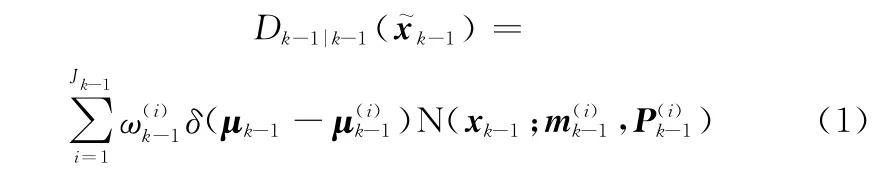

则该滤波器第k时刻的预测强度函数为

假设目标的类别信息不随时间发生改变,则结合式(2),式(3)可以重新记为
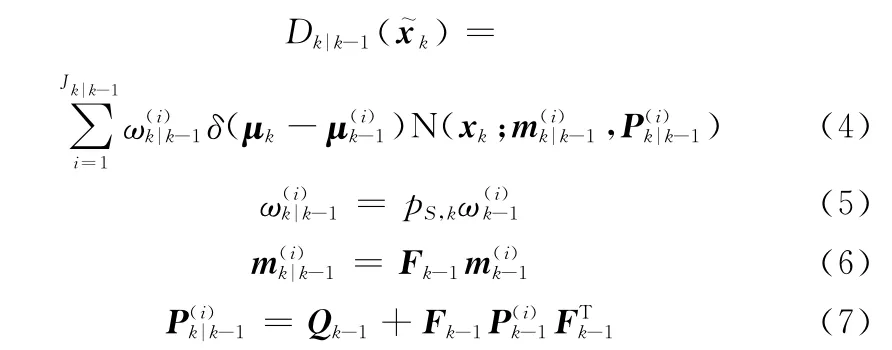
式中,Jk|k-1=Jk-1+Jγ,k表示高斯分量的个数;pS,k表示目标的存活概率;Fk-1表示状态转移矩阵;Qk-1表示过程噪声的协方差矩阵。
步骤2 更新
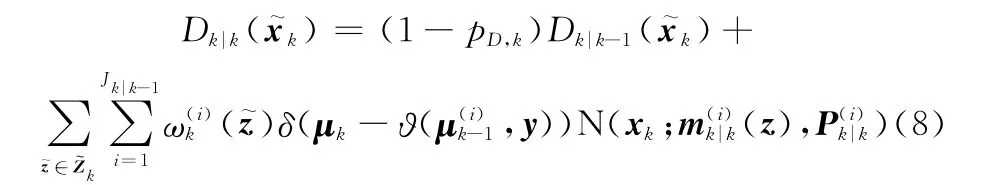
相应的权值为
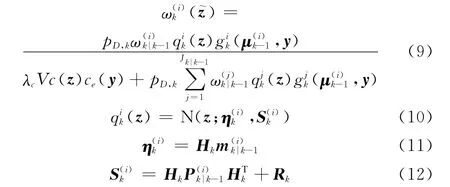
式中,pD,k表示目标的检测概率;λc表示平均杂波密度;V表示监视区域的大小;cz(z)为监视区域内的空间分布函数;Hk表示量测矩阵;Rk表示量测噪声的协方差矩阵。式(8)中高斯分量的均值和方差分别为
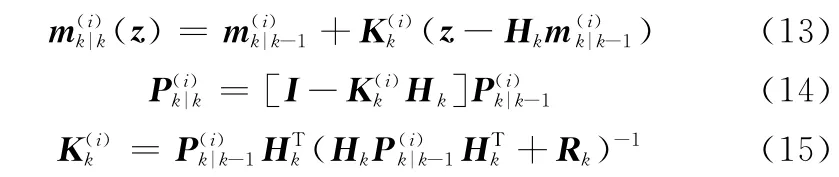
步骤3 目标状态提取
更新后,通常还要对高斯项进行裁剪和合并,以抑制高斯项个数的快速增长,具体过程可见文献[10]。经过处理后的强度函数可以重新记为
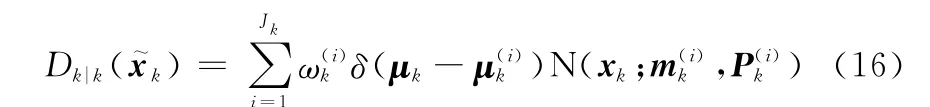
最后,将权值超过一定阈值的高斯项作为目标状态的估计结果,比如

2 类别属性信息的证据转换及相似性度量
由于辐射源目标的信号参数信息无法直接应用于上述滤波器,因此需要结合其他方法对其进行改进。为了便于理解,先给出本文方法实现的基本框图,如图1所示。

图1 基于雷达辐射源信息辅助的目标跟踪算法框图
2.1 可传递信度模型
由于雷达辐射源信号的识别结果为雷达的类型,而已知目标的分类信息一般为平台的类别信息,两者不属于同一辨识框架,不能直接进行比较,所以需要进行证据转换。本文主要利用可传递信度模型[16](transferable belief model,TBM)进行相关的信息处理,它是D-S证据理论的一个扩展。假设Ω为一个辨识框架,它由有限个互斥的元素组成。
定义1 基本信度分配(basic belief assignment,BBA)。若函数m:2Ω→[0,1]满足
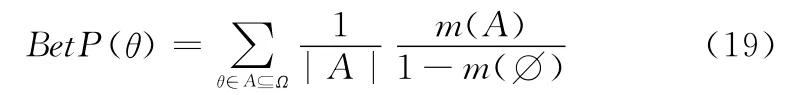
定义3 贝叶斯信度函数。当|A|≠1时,若BBAm满足m(A)=0,则称m为框架Ω上的一个贝叶斯信度函数。
定义4 边缘化[18]。假设Θ和Δ为两个辨识框架,mΩ为框架Ω=Θ×Δ上的一个BBA,则在框架Θ上的边缘化mΩ可以表示为


则称m为框架Ω上的一个BBA。与经典的D-S证据理论不同的是,在TBM中不要求有m(Ø)=0(m(Ø)表示未知的情况)成立。
定义2 Pignistic概率。Pignistic概率是将信度度量转换为概率度量的结果[17],具体定义为
其中,W↓Θ={x:x∈Θ,W∩(x,Δ)≠Ø}。
定义5 条件基本信度分配。对于辨识框架Θ中的元素θ,条件基本信度分配mΔ[θ]表示给定θ的条件下辨识框架Δ上的一个信度函数。
定义6 Dempster信度合成规则。假设m1和m2是同一辨识框架内的两个BBA,其Dempster信度合成规则定义为

定理1[18]假设mΔ[θ](θ∈Θ)为归一化的条件基本信度分配,PΘ为一个贝叶斯信度函数,则对于任意的W⊆Ω,辨识框架Ω=Θ×Δ上的BBAmΩ可以表示为
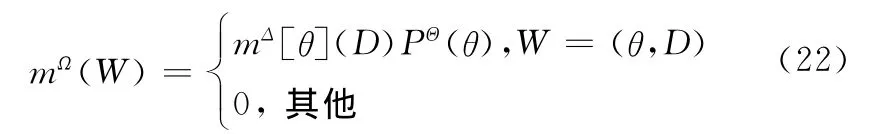
定理2[18]令mΔ=mΩ↓Δ,则对于任意的D⊆Δ,结合定理1和定义4有
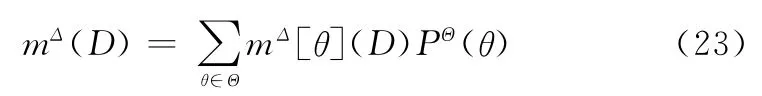
2.2 雷达辐射源识别
电子侦察系统获得的雷达辐射源信息是关于雷达载频等特征参数的信息,而不是类别属性信息,因此需要利用识别算法以确定相应的雷达类型,获得其类别信息。假设模板数据库中有N类雷达:R1,R2,…,RN;对于每一类雷达Ri(i=1,2,…,N)都有L种特征参数,即信号参数ri=(ri1,ri2,…,riL),其中rij表示模板库中第i类雷达的第j种特征参数;同样可以用yj表示待识别辐射源信号的第j种特征参数。本文采用模糊匹配的方法,通过引入高斯型隶属度函数计算待识别信号与模板库中第i种雷达辐射源之间关于第j种特征参数的相似度dij,具体公式为
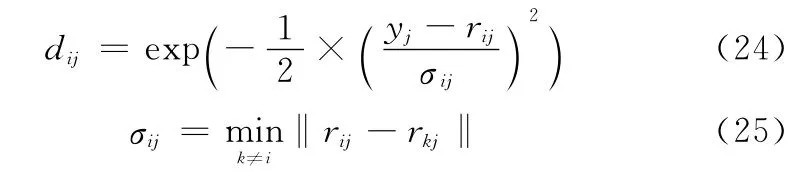
式中,σij为隶属度函数的宽度参数。对每种特征参数的相似度分别进行归一化,得到待识别信号关于各种类型雷达的匹配概率

式中,sj(Ø)表示不可知的情况(在证据理论中也可以认为是一种证据冲突量)。当总的相似度时,说明该待识别信号与模板雷达的匹配程度很低,可能不属于已知的雷达类型。由于每种特征参数都表征了雷达辐射源的某一特性,因此根据每种特征参数计算得到的匹配概率都可以看成是一条证据。当待识别信号属于模板库中某一类型的雷达时,各种特征参数证据之间的冲突应该较小;相反,当各种特征参数证据之间的冲突较大时,说明该待识别信号可能不属于已知雷达类型,应该对其匹配概率进行修正,将更多的概率赋予不可知的情况。本文利用相容系数来描述证据之间的冲突,两个证据si与sj关于命题Rk的相容系数[19]定义为

当si(Rk)=sj(Rk)时,Qij(Rk)=1说明两个证据关于命题Rk的看法是一致的,不存在冲突,即待识别信号与已知雷达类型Rk的第i种及第j种特征参数的匹配程度一致。该系数表示了两个证据之间相互支持度,当一条证据被其他证据支持的程度越高时,说明该证据的可信度越高[19]。
证据si关于命题Rk的可信度定义为

利用该可信度对原始的匹配概率进行修正

在此,假设已有的雷达模板库是完整的,即不考虑未知的雷达类型,因此可以将上述的关于不可知情况的匹配概率赋予杂波R0,即s′i(R0)=s′i(Ø)。则侦获的辐射源信号关于雷达类型的属性信息可以用证据表示为

式中,Θ={Ri:i=0,1,…,N};wj表示各种特征参数的权值,可以根据专家知识进行主观设定,也可以通过分析已知样本进行客观设定。
2.3 类别信息转换
雷达与平台之间存在着一定的配属关系,该关系可以用矩阵A进行表示

式中,aij表示雷达类型为Rj时目标类型为Ti的概率。需要说明的是,ai0表示辐射源信号为杂波时目标为Ti的概率;a0j表示雷达类型为Rj时目标为虚假目标的概率。根据第2.1节的定义5,可以将上述矩阵转换成相应的条件基本信度分配,即
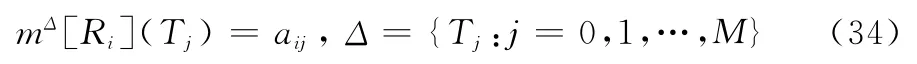
根据第2.1节的定义3及式(32)可知,mΘ为框架Θ上的一个贝叶斯信度函数,因此根据式(34)及第2.1节的定理1,框架Ω=Θ×Δ上的BBA mΩ可以表示为

由于已知目标的分类信息一般为平台的类别信息,因此需要对联合框架Ω中的证据进行边缘化处理转换到目标框架Δ中,以满足同一框架内的证据一致性比较。根据第2.1节的定义4及定理2,雷达辐射源类型框架中的证据转换成目标平台框架中的证据可以表示为

2.4 证据相似性度量
文献[20]对已有的一些证据距离度量方法进行了较好的总结分析,而本文主要将证据信息转换成Pignistic概率后,再利用相容系数进行证据的相似性度量。假设两个证据的BBA为和,根据第2.1节的定义2获得的Pignistic概率分别为BetPi和BetPj,则它们的相似性可用相容系数表示为

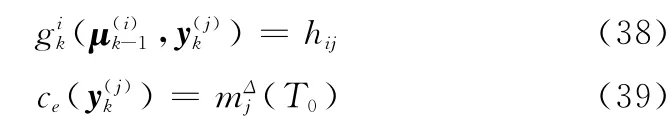
3 仿真实验
仿真实验主要针对不同杂波密度的环境下,对本文提出的GM-C-PHD滤波器与标准GM-PHD滤波器的目标跟踪性能进行比较。每种情况进行500次蒙特卡罗仿真实验。使用的评价指标为最优次模式分配[21](optimal subpattern assignment,OSPA)距离,它可以同时衡量目标个数和目标状态的估计精度,OSPA距离越小说明跟踪算法的性能越好。
3.1 目标运动模型和参数设置
假设在二维直角坐标系中对场景进行监测,目标的运动状态信息包括X轴坐标位置、Y轴坐标位置、X轴方向的速度和Y轴方向的速度,其状态向量可以表示为x=[x,˙x,y,˙y]T。目标做匀速直线运动,其状态方程为
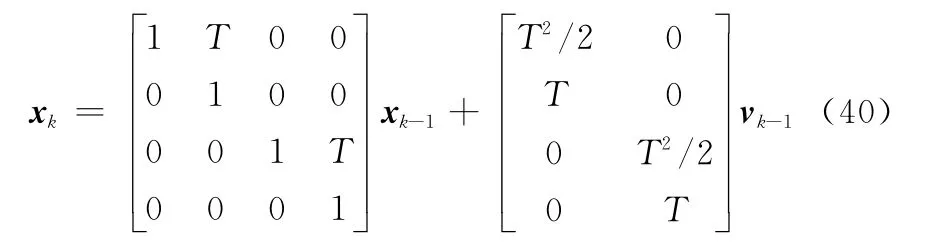
式中,T=1s表示采样间隔;过程噪声vk-1为零均值的高斯白噪声,其协方差矩阵为
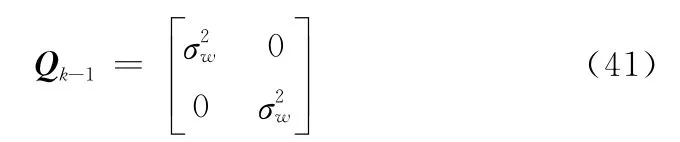
实验中令σw=2m/s2。同时为简单起见,假设辐射源信号的参数信息只包括载频、重复脉冲间隔和脉宽,它们是雷达辐射源信号分选、识别中最常用的3种基本特征。且假设这些参数是时不变的,只会产生一些抖动
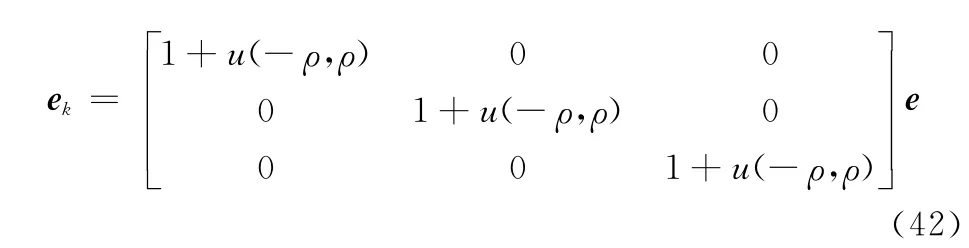
式中,u(-ρ,ρ)表示在区间[-ρ,ρ]内均匀分布,实验中ρ=2%。
辐射源目标的量测方程为

式中,量测噪声wk和we均为零均值的高斯白噪声,其协方差矩阵分别为
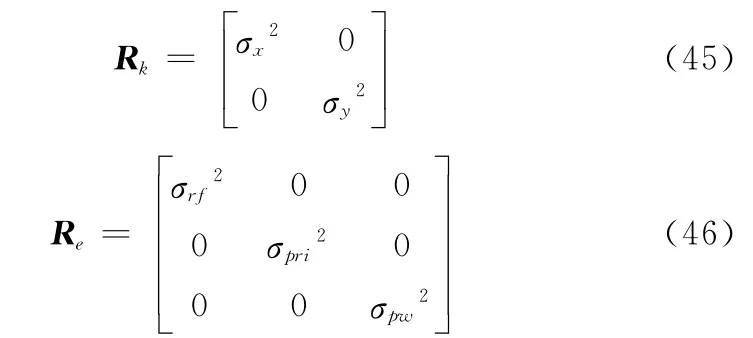
实验中令σx=σy=10m,σrf=30MHz,σpri=10μs,σpw=0.1μs。
目标的检测概率为pD,k=0.98,总的采样时间长度为100s,观测区域为V=[-1 000,1 000]×[-1 000,1 000]m2,杂波的个数服从泊松分布且杂波的位置在观测区域内均匀分布。杂波的载频、重复脉冲间隔及脉宽分别在区间[0MHz,2 000MHz]、[0μs,3 000μs]和[0μs,10μs]内均匀分布。在GM-PHD算法中,目标存活概率pS,k=0.95,最大高斯项个数Jmax=100,高斯裁剪门限Tprune=10-5,合并阈值Umerge=4。OSPA距离中的参数分别设置为p=2和c=100。
3.2 实验结果与分析
仿真实验中假设只有3种平台类型,GM-PHD的目标出生强度函数γk()为

其中


雷达模板库中总共有4种已知雷达类型R1、R2、R3和R4,其参数分别为

仿真场景中有3个目标,具体的运动情况如图2所示。其中辐射源平台目标1和目标3装备的雷达类型都为R1,平台目标2装备的雷达类型为R2。
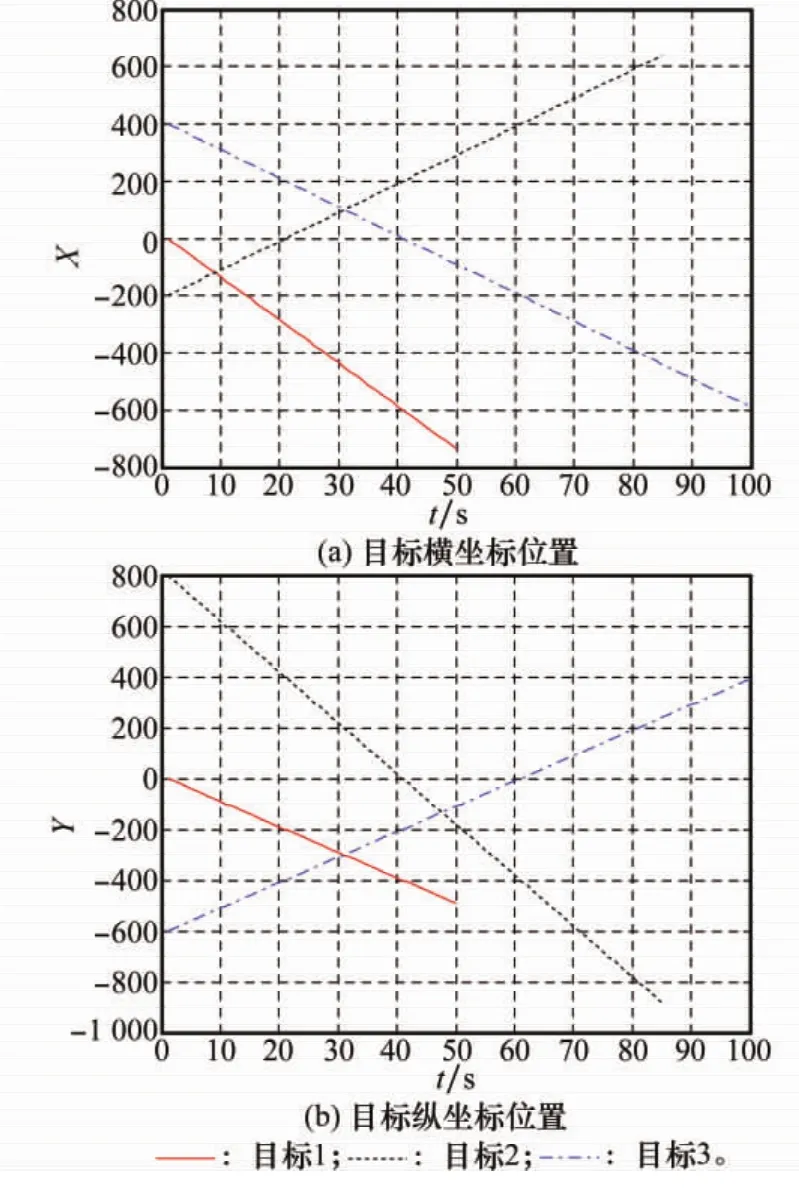
图2 目标的运动场景
图3展示了两种滤波器目标跟踪结果的一个示例,通过观察可以直观看到GM-C-PHD滤波器估计的目标状态个数更加的准确。而图4则对比了在杂波密度为0.15× 10-4(平均每个时刻产生60个杂波)的情况下两种算法的跟踪性能。可以看出,虽然两条曲线的整体趋势是一致的,但本文方法的OSPA值显然小于标准的GM-PHD滤波算法。为了进一步说明本文方法的有效性,比较了不同杂波密度环境下两种跟踪算法的平均OSPA值,如图5所示。从图中可以看出,本文的方法比标准的GM-PHD滤波算法具有更好的目标跟踪性能,而且这种优势随着杂波密度的增大体现得更加明显。这很好地说明了本文提出的结合类别信息的GM-C-PHD滤波器确实能够有效地提高密集杂波环境下雷达辐射源目标跟踪的性能。

图3 滤波器目标跟踪结果比较
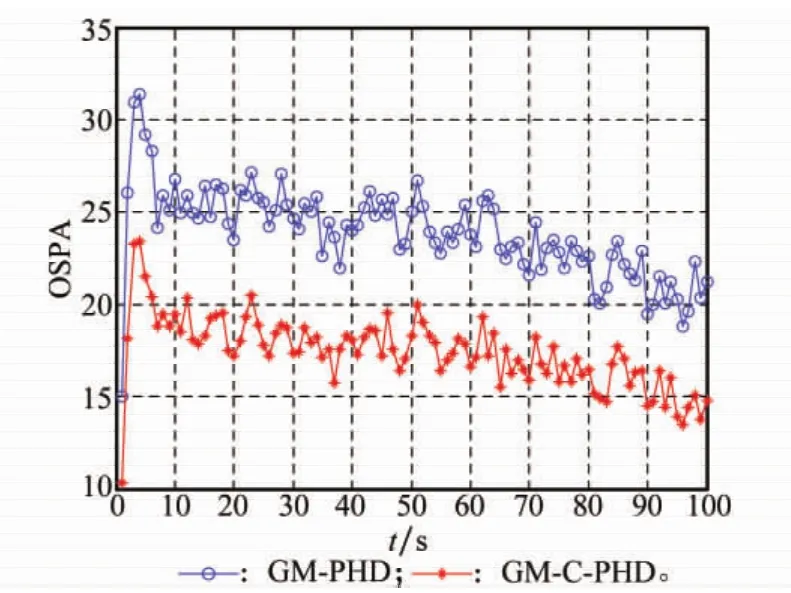
图4 固定杂波密度下的OSPA值比较
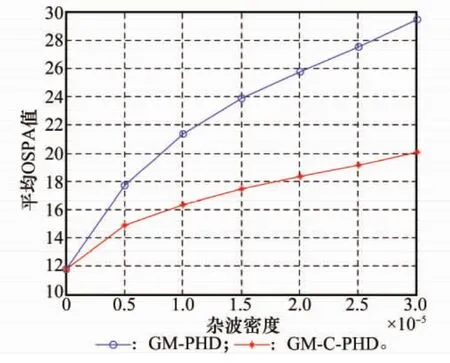
图5 不同杂波密度下的平均OSPA值比较
4 结 论
针对多个雷达辐射源目标的跟踪问题,利用雷达辐射源信号特征,本文提出了一种结合目标类别信息的改进GM-PHD滤波算法。基于雷达辐射源识别和TBM,该方法将雷达辐射源信号信息转换成平台目标类别信息并引入到GM-PHD滤波器高斯分量权重的计算过程当中。与标准的基于GM-PHD滤波器的目标跟踪算法相比,本文提出的方法能够获得更好的目标跟踪效果,对于提高现代战场监视系统的性能具有一定的参考作用。
[1]Xiu J J,He Y,Xiu J H.Study on passive tracking algorithm of targets in clutter[J].Systems Engineering and Electronics,2012,34(2):227-230.(修建娟,何友,修建华.杂波环境下目标无源跟踪算法[J].系统工程与电子技术,2012,34(2):227-230.)
[2]Ding F,Huang J C,Yan K Y.Research on passive data association problems based on transmitter parameters[J].Journal of Astronautics,2013,34(5):721-727.(丁锋,黄建冲,颜坤玉.基于辐射源参数信息的无源数据关联问题研究[J].宇航学报,2013,34(5):721-727.)
[3]Mahler R.Multi-target Bayes filtering via first-order multi-target moments[J].IEEE Trans.on Aerospace and Electronic Systems,2003,39(4):1152-1178.
[4]Ulmke M,Erdinc O,Willett P.GMTI tracking via the Gaussian mixture cardinalized probability hypothesis density filter[J].IEEE Trans.on Aerospace and Electronic Systems,2010,46(4):1821-1833.
[5]Wang Y D,Wu J K,Kassim A A,et al.Data-driven probability hypothesis density filter for visual tracking[J].IEEE Trans.on Circuits and Systems for Video Technology,2008,18(8):1085-1095.
[6]Wang X,Han C Z.An improved multiple model GM-PHD filter for maneuvering target tracking[J].Chinese Journal of Aeronautics,2013,26(1):179-185.
[7]Tong H S,Zhang H,Meng H D,et al.Probability hypothesis density filter multitarget track-before-detect application[J].Acta Electronica Sinica,2011,39(9):2046-2051.(童慧思,张颢,孟华东,等.PHD滤波器在多目标检测前跟踪中的应用[J].电子学报,2011,39(9):2046-2051.)
[8]Mahler R.Approximate multisensor CPHD and PHD filters[C]∥Proc.of the 13th International Conference on Information Fusion,2010:1-8.
[9]Uney M,Clark D E,Julier S J.Distributed fusion of PHD filters via exponential mixture densities[J].IEEE Journal of Selected Topics in Signal Processing,2013,7(3):521-531.
[10]Vo B N,Ma W K.The Gaussian mixture probability hypothesis density filter[J].IEEE Trans.on Signal Processing,2006,54(11):4091-4104.
[11]Zhan R H,Zhang J.Feature-aided data association:a survey[J].Systems Engineering and Electronics,2011,33(1):35-41.(占荣辉,张军.特征辅助数据关联研究综述[J].系统工程与电子技术,2011,33(1):35-41.)
[12]Bar-Shalom Y,Kirubarjan T,Gokberk C.Tracking with classification-aided multiframe data association[J].IEEE Trans.on Aerospace and Electronic Systems,2005,41(3):868-878.
[13]Guo L,Tang B,Liu G.Data association based on target signal classification information[J].Journal of Systems Engineering and Electronics,2008,19(2):246-251.
[14]Yang W,Fu Y W,Li X,et al.Joint detection,tracking and classification algorithm for multiple maneuvering targets based on LGJMS-GMPHDF[J].Journal of Electronics and Information Technology,2012,34(2):398-403.(杨威,付耀文,黎湘,等.基于LGJMS-GMPHDF的多机动目标联合检测、跟踪与分类算法[J].电子与信息学报,2012,34(2):398-403.)
[15]Liu W Q,Yuan B,Li Z J,et al.Track-to-track association algorithm for infrared sensor and ESM based on classification-aided grey relational degree[J].Signal Processing,2011,27(9):1385-1390.(刘万全,袁斌,李中杰,等.基于类型辅助灰色关联度的红外传感器和ESM航迹关联算法[J].信号处理,2011,27(9):1385-1390.)
[16]Smets P,Kennes R.The transferable belief model[J].Artificial Intelligence,1994,66(2):191-234.
[17]Ristic B,Smets P.Target identification using belief functions and implication rules[J].IEEE Trans.on Aerospace and Elec-tronic Systems,2005,41(3):1097-1103.
[18]Smets P.Decision making in the TBM:the necessity of the pignistic transformation[J].International Journal of Approximate Reasoning,2005,38(2):133-147.
[19]Li L L,Ma D J,Wang C S,et al.New method for conflict evidence processing in D-S theory[J].Application Research of Computers,2011,28(12):4528-4531.(李玲玲,马东娟,王成山,等.DS证据理论冲突处理新方法[J].计算机应用研究,2011,28(12):4528-4531.)
[20]Jousselme A L,Maupin P.Distances in evidence theory:comprehensive survey and generalizations[J].Journal of Approximate Reasoning,2012,53(2):118-145.
[21]Schuhmacher D,Vo B T,Vo B N.A consistent metric for performance evaluation of multi-object filters[J].IEEE Trans.on Signal Processing,2008,56(8):3447-3457.
E-mail:zhu_youqing@163.com
周石琳(1965-),男,教授,博士,主要研究方向为计算机视觉、图形图像处理与可视化。
E-mail:slzhoumailbox@gmail.com
Classification-aided GM-PHD filter based on signal feature of radar emitter
ZHU You-qing,ZHOU Shi-lin
(Department of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China)
Tracking for radar emitter targets plays an important role in the field of military application.Although combining with the target classification information is helpful to improve the multi-target tracking performance of the Gaussian mixture-probability hypothesis density(GM-PHD)filter,the signal information of the radar emitter received by the electronic reconnaissance system cannot be applied to the above filter directly.Therefore,this paper first makes use of the signal features to identify the radar types,then based on the transferable belief model the recognition results are transformed into the same frame of the known classification information according to the radar-platform affiliation.Based on that,their similarity measured by the compatibility ratio is used to approximate the likelihoods in the GM-PHD filter.As a result,a modified GM-PHD filter with the classification information can be implemented.The simulation results show that the proposed method can effectively improve the tracking performance of the GM-PHD filter in the scenarios with different clutter densities.
multi-target tracking;Gaussian mixture-probability hypothesis density(GM-PHD)filter;signal of radar emitter;transferable belief model
TP 391
A
10.3969/j.issn.1001-506X.2015.06.08
朱友清(1984-),男,博士研究生,主要研究方向为海上目标关联、多源卫星信息处理。
1001-506X(2015)06-1273-07
2014-08-27;
2014-11-09;网络优先出版日期:2014-12-11。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20141211.1840.005.html
